Multivariate Random Variables

After completing this reading, you should be able to:

• Explain how a probability matrix can be used to express a probability mass function (PMF).
• Compute the marginal and conditional distributions of a discrete bivariate random variable.
• Explain how the expectation of a function is computed for a bivariate discrete random variable.
• Define covariance and explain what it measures.
• Explain the relationship between the covariance and correlation of two random variables and how these are related to the independence of the two variables.
• Explain the effects of applying linear transformations on the covariance and correlation between two random variables.
• Compute the variance of a weighted sum of two random variables.
• Compute the conditional expectation of a component of a bivariate random variable.
• Describe the features of an iid sequence of random variables.
• Explain how the iid property is helpful in computing the mean and variance of a sum of iid random variables.

Multivariate Random Variables

Multivariate random variables accommodate the dependence between two or more random variables. The concepts in the multivariate random variables (such as expectations and moments) are analogous to those under univariate random variables.

Multivariate Discrete Random Variables

Multivariate random variables involve defining several random variables simultaneously on a sample space. In other words, multivariate random variables are vectors of random variables. For instance, a bivariate random variable X can be a vector with two components \(\text X_1\) and \(\text X_2\) with the corresponding realizations being \(\text x_1\) and \(\text x_2\), respectively.

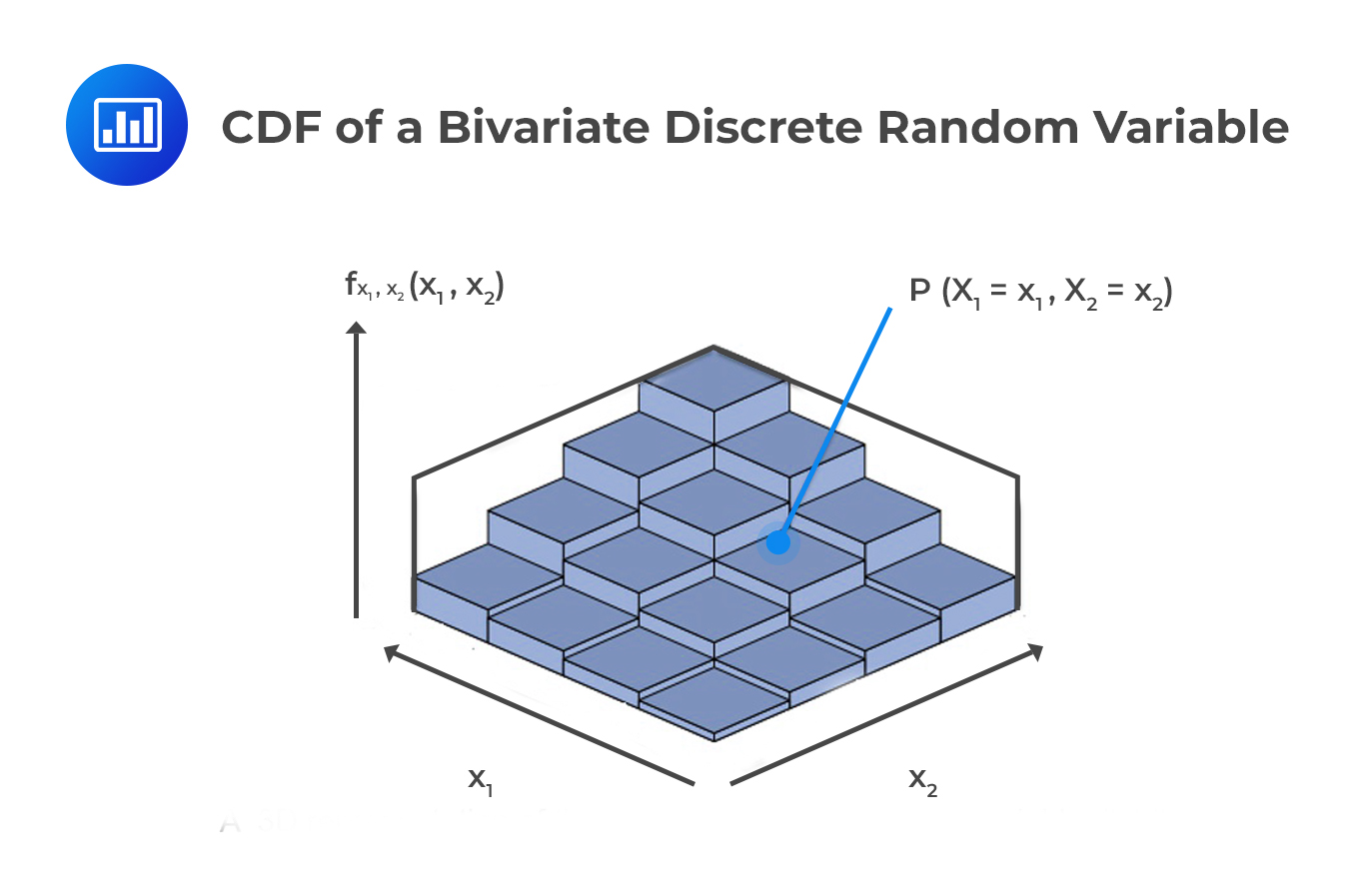
The PMF or PDF for a bivariate random variable gives the probability that the two random variables each take a certain value. If we wish to plot these functions, we would need three factors: \(\text X_1\), \(\text X_2\), and the PMF/PDF. This is also applicable to the CDF.

The Probability Mass Function (PMF)

The PMF of a bivariate random variable is a function that gives the probability that the components of X=x takes the values \(\text X_1=\text x_1\) and \(\text X_2=\text x_2\). That is:

$$ {\text f}_{\text X_1,\text X_2} (\text x_1,\text x_2 )={\text P}(\text X_1=\text x_1,\text X_2=\text x_2 ) $$

The PMF explains the probability of realization as a function of \(\text x_1\) and \(\text x_2\). The PMF has the following properties:

1. \({\text f}_{\text X_1,\text X_2} (\text x_1,\text x_2 ) \ge 0\)
2. \(\sum_{\text x_1} \sum_{\text x_2} {\text f}_{\text X_1,\text X_2 } (\text x_1,\text x_2 )=1\)

Example: Trinomial Distribution

The trinomial distribution is the distribution of n independent trials where each trial results in one of the three outcomes (a generalization of the binomial distribution). The first, second and the third components are \(\text X_1, \text X_2\) and \(\text n- {\text X}_1- {\text X}_2\) respectively. However, the third component is redundant provided that we know \(\text X_1\) and \(\text X_2\).

The trinomial distribution has three parameters:

1. n, representing the total number of the trials
2. \(\text p_1\), representing the probability of realizing \(\text X_1\)
3. \(\text p_2\), representing the probability of realizing \(\text X_2\)

Intuitively, the probability of observing \(\text n- {\text X}_1- {\text X}_2\) is:

$$ 1- \text p_1- \text p_2 $$

The PMF of the trinomial distribution, therefore, is given by: $$ {\text f}_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\cfrac {{\text n}!}{{\text x}_1 ! {\text x}_2 !( \text n-\text x_1-\text x_2 )!} \text p_1^{\text x_1} \text p_2^{\text x_2 } (1- \text p_1- \text p_2 )^{\text n- \text x_1- \text x_2} $$

The Cumulative Distribution Function (CDF)

The CDF of a bivariate discrete random variable returns the total probability that each component is less than or equal to a given value. It is given by:

$$ \text F_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\text P(\text X_1 < \text x_1,\text X_2 < \text x_2 )=\sum _{ { \text t }_{ 1 }\epsilon {\text R}\left( { \text X }_{ 1 } \right) \\ { \text t }_{ 1 }\le { \text x }_{ 1 } }^{ }{ \sum _{ { \text t }_{ 2 }\epsilon { \text R}\left( \text X_{ 2 } \right) \\ { \text t }_{ 2 }\le { \text x }_{ 2 } }^{ }{ \text f_{ ( \text X_{ 1 }, \text X_{ 2 }) }( \text t_{ 1 }, \text t_{ 2 }) } } $$

In this equation, \(\text t_{ 1 }\) contains the values that \(\text X_1\) may take as long as \(\text t_1 \le \text x_1\). Similarly, \(\text t_2\) contains the values that \(\text X_2\) may take as long as \(\text t_2 \le \text x_2\)

Probability Matrices

The probability matrix is a tabular representation of the PMF.

Example: Probability Matrix

In financial markets, market sentiments play a role in determining the return earned on a security. Suppose the return earned on a bond is in part determined by the rating given to the bond by analysts. For simplicity, we are going to assume the following:

• There are only three possible returns :10%, 0%, or -10%
• Analyst ratings (sentiments) can be positive, neutral, or negative

We can represent this in a probability matrix as follows:

$$ \begin{array}{c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} \\\hline \text{Analyst} & \text{Positive} & \bf{+1} & {5\%} & {5\%} & {30\%} \\ \bf{(\text X_2)} & \text{Neutral} & \bf{0} & {10\%} & {10\%} & {15\%} \\ {} & \text{Negative} & \bf{-1} & {20\%} & {5\%} & {0\%} \\ \end{array} $$

Each cell represents the probability of a joint outcome. For example, there’s a 5% probability of a negative return (-10%) if analysts have positive views about the bond and its issuer. In other words, there’s a 5% probability that the bond will decline in price with a positive rating. Similarly, there’s a 10% chance that the bond’s price will not change (and hence a zero return) given a neutral rating.

The Marginal Distribution

The marginal distribution gives the distribution of a single variable in a joint distribution. In the case of bivariate distribution, the marginal PMF of \(\text X_1\) is computed by summing up the probabilities for \(\text X_1\) across all the values in the support of \(\text X_2\). The resulting PMF of \(\text X_1\) is denoted by \(f_{\text X_1 } (\text x_1 )\), i.e., the marginal distribution of \(\text X_1\).

$$ \text f_{X_1} (\text x_1 )=\sum_{\text x_2 \epsilon {\text R}(\text X_2 )} \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) $$ Intuitively, the PMF of \(\text X_2\) is given by:

$$ \text f_{X_2} (\text x_2 )=\sum_{\text x_1 \epsilon {\text R}(\text X_1 )} \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) $$

Example: Computing the Marginal Distribution

Using the probability matrix, we created above, we can come up with marginal distributions for both \(\text X_1\) (return) and \(\text X_2\) (analyst ratings) as follows:

For \(\text X_1\),

$$ \begin{align*} \text P(\text X_1=-10\%)& =5\%+20\%+10\%=35\% \\ \text P(\text X_1=0\%) & =5\%+10\%+5\%=20\% \\ \text P(\text X_1=+10\%) & =30\%+15\%+0\%=45\% \\ \end{align*} $$ For \(\text X_2\), $$ \begin{align*} \text P(\text X_2=+1)& =5\%+5\%+30\%=40\% \\ \text P(\text X_2=0) & =10\%+10\%+15\%=35\% \\ \text P(\text X_2=-1) & =20\%+5\%+0\%=25\% \\ \end{align*} $$

We wish to compute the marginal distribution of the returns. 

In summary, for example, the marginal distribution of \(\text X_1\) is given below:

$$ \begin{array}{c|c|c|c} \bf{\text{Return}(\text X_1)} & \bf{-10\%} & \bf{0\%} & \bf{10\%} \\ \hline \bf{\text{P}(\text X_1=\text x_1)} & {35\%} & {20\%} & {45\%} \\ \end{array} $$

$$ \begin{array}{c|c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} & \bf{\text f_{\text X_2 } (\text x_2 )} \\\hline \textbf{Analyst } & \textbf{Positive} & \bf{+1} & {5\%} & {5\%} & {30\%} & {40\%} \\ \bf{(\text X_2)} & \textbf{Neutral} & \bf{0} & {10\%} & {10\%} & {15\%} & {35\%} \\ {} & \textbf{Negative} & \bf{-1} & {20\%} & {5\%} & {0\%} & {25\%} \\ \hline {} & {\bf{\text f_{\text X_1 } (\text x_1 )}} &{} & {{35\%}} & {{20\%}} & {{45\%}} & {} \\ \end{array} $$

As you may have noticed, the marginal distribution satisfies the property of the ideal probability distribution. That is:

$$ \sum_{\forall {\text X}_1} \text f_{\text X_1} (\text x_1 )=1 $$ And $$ \text f_{\text X_1} (\text x_1 ) \ge 0 $$

This is true because the marginal PMF is a univariate distribution.

We can, in addition, use the marginal PMF to compute the marginal CDF. The marginal CDF is such that, \(\text P(\text X_1 < \text x_1 )\). That is:

$$ \text F_{\text X_1} (\text x_1 )=\sum_{{ \text t }_{ 1 }\epsilon R\left( { \text X }_{ 1 } \right) \\ {\text t }_{ 1 }\le {\text x }_{ 1 }} \text f_{\text X_1 } (\text t_1 ) $$

Independence of Random Variables

Recall that if the two events A and B are independent then:

$$ \text P(\text A \cap \text B)=\text P(\text A)\text P(\text B) $$

This principle applies to bivariate random variables as well. If the distributions of the components of the bivariate distribution are independent, then:

$$ \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\text f_{\text X_1 } (\text x_1 ) \text f_{\text X_2} (\text x_2 ) $$

Example: Independence of Random Variables

Now let’s use our earlier example on the return earned on a bond. If we assume that the two variables – return and ratings – are independent, we can calculate the joint distribution by multiplying their marginal distributions. But are they really independent? Let’s find out! We have already established the joint and the marginal distributions, as reproduced in the following table.

$$ \begin{array}{c|c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} & \bf{\text f_{\text X_2 } (\text x_2 )} \\\hline \textbf{Analyst } & \textbf{Positive} & \bf{+1} & {5\%} & {5\%} & {30\%} & {40\%} \\ \bf{(\text X_2)} & \textbf{Neutral} & \bf{0} & {10\%} & {10\%} & {15\%} & {35\%} \\ {} & \textbf{Negative} & \bf{-1} & {20\%} & {5\%} & {0\%} & {25\%} \\ \hline {} & {\bf{\text f_{\text X_1 } (\text x_1 )}} &{} & {{35\%}} & {{20\%}} & {{45\%}} & {} \\ \end{array} $$

So assuming that our two variables are independent, our joint distribution would be as follows:

$$ \begin{array}{c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} \\\hline \textbf{Analyst } & \textbf{Positive} & \bf{+1} & {14\%} & {8\%} & {18\%} \\ \bf{(\text X_2)} & \textbf{Neutral} & \bf{0} & {12.25\%} & {7\%} & {15.75\%} \\ {} & \textbf{Negative} & \bf{-1} & {8.75\%} & {5\%} & {11.25\%} \\ \end{array} $$

We obtain the table above by multiplying the marginal PMF of the bond return by the marginal PMF of ratings. For example, the marginal probability that the bond return is 10% is 45% — the sum of the third column. The marginal probability of a positive rating is 40% — the sum of the first row. These two values when multiplied give us the joint probability on the upper left end of the table (18%). $$ 45\% * 40\% = 18\% $$

It is clear that the two variables are not independent because multiplying their marginal PMFs does not lead us back to the joint PMF.

The Conditional Distributions

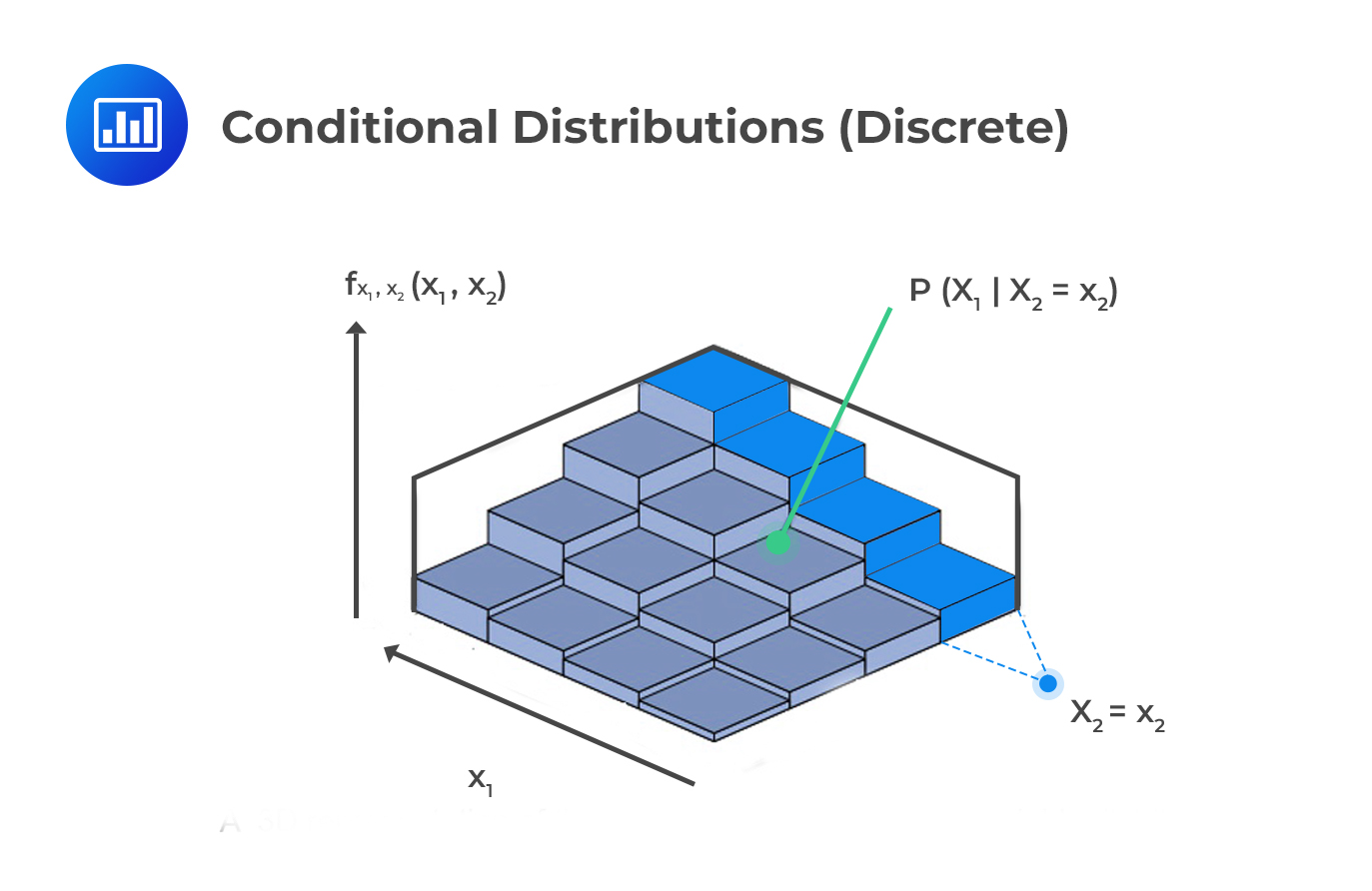
The conditional distributions describe the probability of an outcome of a random variable conditioned on the other random variable taking a particular value.

Recall that, given any two events A and B, then:

$$ \text P(\text A│\text B)=\cfrac {\text P(\text A \cap \text B)}{\text P(\text B) } $$

This result can be applied in bivariate distributions. That is, the conditional distribution of \(\text X_1\) given \(\text X_2\) is defined as:

$$ \text f_{\text X_1│\text X_2} (\text x_1│\text X_2=\text x_2 )=\cfrac {\text f_{\text X_1,\text X_2 } (\text x_1,\text x_2 )}{\text f_{\text X_2} (\text x_2 ) } $$ From the result above, the conditional distribution is joint distribution divided by the marginal distribution of the conditioning variable.

Example: Calculating the Conditional Distribution

$$ \begin{array}{c|c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} & \bf{\text f_{\text X_2 } (\text x_2 )} \\\hline \textbf{Analyst } & \textbf{Positive} & \bf{+1} & {5\%} & {5\%} & {30\%} & {40\%} \\ \bf{(\text X_2)} & \textbf{Neutral} & \bf{0} & {10\%} & {10\%} & {15\%} & {35\%} \\ {} & \textbf{Negative} & \bf{-1} & {20\%} & {5\%} & {0\%} & {25\%} \\ \hline {} & {\bf{\text f_{\text X_1 } (\text x_1 )}} &{} & {{35\%}} & {{20\%}} & {{45\%}} & {} \\ \end{array} $$

Suppose we want to find the distribution of bond returns conditional on a positive analyst rating. The conditional distribution is:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1│\text X_2=1)=\cfrac {\text f_{\text X_1,\text X_2} (\text x_1,X_2=1)}{\text f_{\text X_2 } (\text x_2=1) }=\cfrac {\text f_{\text X_1,\text X_2 } (\text x_1,X_2=1)}{40\%} $$

With this, we can proceed to determine specific conditional probabilities:

$$ \begin{array}{c|c|c|c} {\bf{\text{Returns} (\text X_1)}} & \bf{-10\%} & \bf{0\%} & \bf{10\%} \\ \hline \bf{\text f_{(\text X_1│\text X_2) } (\text x_1│\text X_2=\text x_2 )} & {\frac {5\%}{40\%}=12.5\% } & { \frac {5\%}{40\%}=12.5\% } & {\frac {30\%}{40\%}=75\%} \\ \bf{=\text P(\text X_1=\text x_1|\text X_2=1)} & {} & {} & {} \\ \end{array} $$

What we have done is to take the joint probabilities where there’s a positive analyst rating and then divided these values by the marginal probability of a positive rating (40%) to produce the conditional distribution.

Note that the conditional PMF obeys the laws of probability, i.e.,

1. \(\text f_{(\text X_1│\text X_2 )} (\text x_1│\text X_2=\text x_2 ) \ge 0 \text{(nonnegativity)}\)
2. \(\sum_{\forall(\text X_1│\text X_2 )}\text f_{(\text X_1│\text X_2 )} (\text x_1│\text X_2=\text x_2 ) =1\)

Conditional Distribution for a Set of Outcomes

Conditional distributions can be computed for one variable, while conditioning on more than one variable.

For example, assume that we need to compute the conditional distribution of the bond returns given that analyst ratings are non-negative. Therefore, our conditioning set is {+1,0}:

$$ \text X_2 \in \left\{+1,0 \right\} $$ The conditional PMF must sum across all outcomes in the set that is conditioned on S {+1,0}:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1│\text x_2 \epsilon \text S)=\cfrac { \sum_{\text X_2 \epsilon \text C} \text f_{(\text X_1,\text X_2)} (\text x_1,\text x_2 ) }{\sum_{\text X_2 \epsilon \text C} \text f_{(\text X_2 )} (\text x_2 ) } $$

The marginal probability that \(\text X_2 \in \left\{+1,0\right\}\) is the sum of the marginal probabilities of these two outcomes:

$$ \text f_{\text x_2} (+1)+\text f_{\text x_2} (0)=75\% $$

$$ \begin{array}{c|c|c|c|c|c|c} {} & {} & {} & \textbf{Bond} & \textbf{Return} & \bf(\text X_1) \\ {} & {} & {} & \bf{-10\%} & \bf{0\%} & \bf{10\%} & \bf{\text f_{\text X_2 } (\text x_2 )} \\\hline \textbf{Analyst } & \textbf{Positive} & \bf{+1} & {5\%} & {5\%} & {30\%} & {40\%} \\ \bf{(\text X_2)} & \textbf{Neutral} & \bf{0} & {10\%} & {10\%} & {15\%} & {35\%} \\ {} & \textbf{Negative} & \bf{-1} & {20\%} & {5\%} & {0\%} & {25\%} \\ \hline {} & {\bf{\text f_{\text X_1 } (\text x_1 )}} &{} & {{35\%}} & {{20\%}} & {{45\%}} & {} \\ \end{array} $$

Thus, the conditional distribution is given by:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1│\text x_2 \epsilon \left\{+1,0 \right\})=\begin{cases} \frac { 5\%+10\% }{ 75\% } =20\% \\ \frac { 5\%+10\% }{ 75\% } =20\% \\ \frac { 30\%+15\% }{ 75\% } =60\% \end{cases} $$

Independence and Conditional Distribution of Random Variables

Recall that the conditional distribution is given by:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1│\text X_2=\text x_2 )=\cfrac {\text f_{ \text X_1,\text X_2} (\text x_1,\text x_2 )}{\text f_{\text X_2} (\text x_2 ) }$$

This can be rewritten into:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1,\text x_2 )=\text f_{(\text X_1│\text X_2)} (\text x_1│\text X_2=\text x_2 ) \text f_{\text X_2} (\text x_2 ) $$ Or $$ \text f_{(\text X_1,\text X_2)} (\text x_1,\text x_2 )=\text f_{\text X_2│\text X_1} (\text x_2│\text X_1=\text x_1 ) \text f_{\text X_1} (\text x_1 ) $$

Also, if the distributions of the components of the bivariate distributions are independent, then:

$$ \text f_{(\text X_1,\text X_2)} (\text x_1,\text x_2 )=\text f_{\text X_1 } (\text x_1 ) \text f_{\text X_2} (\text x_2 ) $$

If we substitute this in the above results we get:

$$ \begin{align*} & \text f_{\text X_1} (\text x_1 ) \text f_{\text X_2} (\text x_2 )=\text f_{(\text X_1│\text X_2) } (\text x_1│\text X_2=\text x_2 ) \text f_{\text X_2} (\text x_2 ) \\ & \Rightarrow \text f_{\text X_1 } (\text x_1 )=\text f_{(\text X_1│\text X_2) } (\text x_1│\text X_2=\text x_2 ) \\ \end{align*} $$

Applying again to

$$ \text f_{\text X_1,\text X_2 } (\text x_1,\text x_2 )=\text f_{(\text X_2│\text X_1)} (\text x_2│\text X_1=\text x_1 ) \text f_{\text X_1 } (\text x_1 ) $$

we get:

$$ \text f_{\text X_2} (\text x_2 )=\text f_{(\text X_2│\text X_1 )} (\text x_2│\text X_1=\text x_1 ) $$

Expectations

The expectation of a function of a bivariate random variable is defined in the same way as that of the univariate random variable. Consider the function \(\text g(\text X_1,\text X_2)\). The expectation is defined as:

$$ \text E(\text g(\text X_1,\text X_2 ))=\sum_{\text x_1 \epsilon \text R(\text X_1 )} \sum_{\text x_2 \epsilon \text R(\text X_2 )} \text g(\text x_1,\text x_2) \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) $$

\(\text g(\text x_1,\text x_2\) depends on both \(\text x_1\) and \(\text x_2)\) and it may be a function of one component only. Just like the univariate random variable,

$$ \text E(\text g(\text X_1,\text X_2 )) \neq \text g(\text E(\text X_1 ),\text E(\text X_2)) $$

for a nonlinear function \(\text g(\text x_1,\text x_2)\).

Example: Calculating the Expectation

Consider the following probability mass function:

$$ \begin{array}{c|c|c|c} \hline {} & {} & \bf{\text X_1} & {} \\ \hline {} & {} & \bf{1} & \bf{2} \\ \bf{X_2} & \bf{3} & {10\%} & {15\%} \\ {} & \bf{4} & {70\%} & {5\%} \\ \hline \end{array} $$

Given that \(\text g(\text x_1,\text x_2 )=\text x_1^{\text x_2 }\) , calculate \(\text E(\text g(\text x_1,\text x_2 ))\)

Solution

Using the formula:

$$ \text E(\text g(\text X_1,\text X_2 ))=\sum_{\text x_1 \epsilon \text R(\text X_1 )} \sum_{\text x_2 \epsilon \text R(\text X_2 )} \text g(\text x_1,\text x_2) \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) $$ In this case we need:

$$ \begin{align*} \text E(\text g(\text X_1,\text X_2 )) & =\sum_{\text x_1 \epsilon \left\{1,2\right\} } \sum_{\text x_2 \epsilon \left\{ 3,4 \right\} } \text g(\text x_1,\text x_2) \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) \\ & =1^3 (0.10)+1^4 (0.7)+2^3 (0.15)+2^4 (0.05) \\ & =2.80 \\ \end{align*} $$

Moments

Just like the univariate random variables, we shall use the expectations to define the moments.

The first moment is defined as:

$$ \text E(\text X)=[\text E(\text X_1 ),\text E(\text X_2 )]=[\mu_1,\mu_2 ] $$

The second moment involves the covariance between the components of the bivariate distribution \(\text X_1\) and \(\text X_2\). The second moment is given by:

$$ \text {Var}(\text X_1+\text X_2 )=\text {Var}(\text X_1 )+\text {Var}(\text X_2 )+2\text {Cov}(\text X_1 \text X_2) $$

The Covariance between \(\text X_1\) and \(\text X_2\) is defined as:

$$ \begin{align*} \text{Cov}(\text X_1,\text X_2 ) & =\text E[(\text X_1-\text E[\text X_1])]\text E[(\text X_2-\text E[\text X_2])] \\ & =\text E[\text X_1 \text X_2 ]-\text E[\text X_1]\text E[\text X_2] \\ \end{align*} $$

Note that \(\text{Cov}(\text X_1,\text X_1 )=\text {Var}(\text X_1)\) and that if \(\text X_1\) and \(\text X_2\) are independent then \(\text E[\text X_1 \text X_2 ]-\text E[\text X_1]\text E[\text X_2]=0\) and thus:

$$ \begin{align*} \text{Cov}(\text X_1,\text X_2 ) & =\text E[\text X_1 \text X_2 ]-\text E[\text X_1]\text E[\text X_2] \\ & =\text E[\text X_1 ]\text E[\text X_2 ]-\text E[\text X_1 ]\text E[\text X_2 ]=0 \\ \end{align*} $$

Most of the correlation between \(\text X_1\) and \(\text X_2\) is reported. Now let \(\text {Var}(\text X_1 )=\sigma_1^2 ,\text {Var}(\text X_2 )=\sigma_2^2\) and \(\text {Cov}(\text X_1,\text X_2 )=\sigma_{12}\) then the correlation is defined as:

$$ \begin{align*} \text{Corr}( \text X_1,\text X_2 )=\rho_{\text X_1 \text X_2}=\cfrac { \text {Cov}(\text X_1,\text X_2) }{ \sqrt{\sigma_1^2 } \sqrt{\sigma_2^2 }}=\cfrac {\sigma_{12}}{\sigma_1 \sigma_2 } \\ \end{align*} $$

Therefore, we can write this in terms of covariance. That is:

$$ \sigma_{12}=\rho_{\text X_1 \text X_2 } \sigma_1 \sigma_2 $$

Correlation gives the measure of the strength of the linear relationship between the two random variables, and it is always between -1 and 1. That is \(-1 < \text{Corr}(\text X_1,\text X_1 ) < 1\)

For instance, if \(\text X_2=\alpha + \beta \text X_1\) then:

$$ \text {Cov}(\text X_1,\text X_2 )=\text {Cov}(\text X_1,\alpha + \beta \text X_1 )=\beta \text{Var}(\text X_1) $$

But we know that \(\text{Var}(\alpha + \beta \text X_1 )=\beta^2 \text{Var}(\text X_1)\). So,

$$ \text{Corr}( \text X_1,\text X_2 )=\rho_{\text X_1 \text X_2}=\cfrac {\beta \text{Var}(\text X_1)}{\sqrt{\text{Var}(\text X_1)} \sqrt { \beta^2 \text{Var}(X_1) } }=\cfrac {\beta}{|\beta|} $$

it is now evident that if \(\beta >0\), then \(\rho_{\text X_1 \text X_2}=1\) and when \(\beta \le 0\) then \(\rho_{\text X_1 \text X_2}=0\)

Similarly, if we consider two scaled random variables \(\text a+\text b \text X_1\) and \(\text c+\text d \text X_2\)

Then,

$$ \text{Cov}(\text a+\text b \text X_1,\text c+\text d \text X_2 )=\text {bd} \text {Cov}(\text X_1,\text X_2) $$

This implies that the scale factor in each random variable multiactivity affects the covariance. Using the above results, the corresponding correlation coefficient of \(\text{aX}_1\) and \(\text{bX}_2\) is given by:

$$ \begin{align*} \text{Corr}(\text a \text X_1,\text b\text X_2 ) & =\cfrac { \text {ab} \text {Cov}(\text X_1,\text X_2)}{ \sqrt{\text a^2 \text {Var}(\text X_1)} \sqrt{\text b^2 \text {Var}(\text X_2)} } =\cfrac {\text {ab}}{|\text{a}||\text{b}|} \cfrac { {\text {Cov}}(\text X_1,\text X_2) }{\sqrt {\text {Var}(\text X_1)} \sqrt {\text {Var}(\text X_2)}} \\ & =\cfrac {\text{ab}}{|\text{a}||\text{b}|} \rho_{\text X_1 \text X_2} \\ \end{align*} $$

Application of Correlation: Portfolio Variance and Hedging

The variance of the underlying securities and their respective correlations are the necessary ingredients if the variance of a portfolio of securities is to be determined. Assuming that we have two securities whose random returns are \(\text X_\text A\) and \(\text X_\text B\) and their means are \(\mu_\text A\) and \(\mu_\text B\) with standard deviations of \(\sigma_A\) and \(\sigma_B\). Then, the variance of \(\text X_\text A\) plus \(\text X_\text B\) can be computed as follows:

$$ \sigma_{\text A+\text B}^2=\sigma_{\text A}^2+\sigma_{\text B}^2+2\rho_{\text {AB}} \sigma_{\text A} \sigma_{\text B} $$

If \(\text X_{\text A}\) and \(\text X_{\text B}\) have a correlation of \(\rho_{\text {AB}}\) between them,

The equation changes to:

$$ \sigma_{\text A+\text B}^2=2\sigma^2 (1+\rho_{\text {AB}}), $$

Where:

$$ \sigma_\text A^2=\sigma_\text B^2=\sigma^2 $$

if both securities have the same variance. If the correlation between the two securities is zero, then the equation can be simplified further. We have the following relation for the standard deviation:

$$ \rho_{\text{AB}}=0 \Rightarrow \sigma_{\text A+\text B}=\sqrt{2 \sigma } $$

For any number of variables, we have that:

$$ \begin{align*} \text Y & =\sum_{\text i=1}^\text n \text X_\text i =1\text n \text X_ \text i \\ \sigma_\text Y^2& =\sum_{\text i=1}^\text n \sum_{\text j=1}^\text n \rho_{\text {ij}} \sigma_\text i \sigma_\text j \\ \end{align*} $$

In case all the \(\text X_\text i\)’s are uncorrelated and all variances are equal to \(\sigma\), then we have:

$$ \sigma_\text Y=\sqrt{\text n \sigma } \text { if } \rho_{\text {ij}}=0 \quad \forall \quad \text i\neq \text j $$

This is what is called the square root rule for the addition of uncorrelated variables.

Suppose that \(\text Y, \text X_\text A\), and \(\text X_\text B\) are such that:

$$ \text Y=\text a\text X_\text A+\text b\text X_\text B $$

Therefore, with our standard notation, we have that:

$$ \sigma_\text Y^2=\text a^2 \sigma_\text A^2+\text b^2 \sigma_\text B^2+2\text {ab} \rho_{\text {AB}} \sigma_\text A \sigma_\text B……………\text{Eq 1} $$

The major challenge during hedging is correlation. Suppose we are provided with $1 of a security A. We are to hedge it with $h of another security B. A random variable p will be introduced to our hedged portfolio. h is, therefore, the hedge ratio. The variance of the hedged portfolio can easily be computed by applying Eq1:

$$ \begin{align*} \text P & =\text X_\text A+\text {hX}_\text B \\ \sigma_\text P^2 & =\sigma_\text A^2+\text h^2 \sigma_\text B^2+2\text h \rho_{\text {AB}} \sigma_A \sigma_B \\ \end{align*}$$

The minimum variance of a hedge ratio can be determined by determining the derivative with respect to h of the portfolio variance equation and then equate it to zero:

$$ \begin{align*} \cfrac {\text d\sigma^2 \text P}{\text{dh}}=2\text h \sigma_\text B^2+2 \rho_{\text{AB}} \sigma_\text A \sigma_\text B=0 \\ \Rightarrow \text h^{*}=-\rho_{\text{AB}} \cfrac {\sigma_\text A}{\sigma_\text B} \\ \end{align*} $$

To determine the minimum variance achievable, we substitute h* to our original equation:

$$ \text{min}[\sigma_\text P^2]=\sigma_\text A^2 (1-\rho_{\text{AB}}^2) $$

The Covariance Matrix

The covariance matrix is a 2×2 matrix that displays the covariance between the components of X. For instance, the covariance matrix of X is given by:

$$ \text{Cov}(\text X)=\begin{bmatrix} { \sigma }_{ 1 }^2 & { \sigma }_{ 12 } \\ { \sigma }_{ 12 } & { \sigma }_{ 2 }^2 \end{bmatrix} $$

The Variance of Sums of Random Variables

The variance of the sum of two random variables is given by:

$$ \text{Var}(\text X_1+\text X_2 )=\text {Var}(\text X_1 )+\text {Var}(\text X_2 )+2\text {Cov}(\text X_1 \text X_2) $$

If the random variables are independent, then \(\text {Cov}(\text X_1 \text X_2 )=0\) and thus:

$$ \text{Var}(\text X_1+\text X_2 )=\text {Var}(\text X_1 )+\text {Var}(\text X_2 ) $$

In case of weighted random variables, the variance is given by:

$$ \text {Var}(\text {aX}_1+ \text {bX}_2 )=\text a^2 \text {Var}(\text X_1 )+\text b^2 \text {Var}(\text X_2 )+2\text {abCov}(\text X_1 \text X_2) $$

Conditional Expectation

A conditional expectation is simply the mean calculated after a set of prior conditions has happened. It is the value that a random variable takes “on average” over an arbitrarily large number of occurrences – given the occurrence of a certain set of “conditions.” A conditional expectation uses the same expression as any other expectation and is a weighted average where the probabilities are determined by a conditional PMF.

For a discrete random variable, the conditional expectation is given by:

$$ \text E(\text X_1│\text X_2=\text x_2 )=\sum_\text i \text x_{1\text i} \text f(\text X_1 |\text X_2=\text x_2) $$

Example: Calculating the Conditional Expectation

In the bond return/rating example, we may wish to calculate the expected return on the bond given a positive analyst rating, i.e., \(\text E(\text X_1│\text X_2=1 )\)

If you recall, the conditional distribution is as follows:

$$ \begin{array}{c|c|c|c} {\bf{\text{Returns} (\text X_1)}} & \bf{-10\%} & \bf{0\%} & \bf{10\%} \\ \hline \bf{\text f_{(\text X_1│\text X_2) } (\text x_1│\text X_2=1 )} & {\frac {5\%}{40\%}=12.5\% } & { \frac {5\%}{40\%}=12.5\% } & {\frac {30\%}{40\%}=75\%} \\ \bf{=\text P(\text X_1=\text x_1|\text X_2=1)} & {} & {} & {} \\ \end{array} $$

The conditional expectation of the return is determined as follows:

$$ \text {E}(\text X_1│\text X_2=1)=-0.10×0.125+0×0.125+0.10×0.75=0.0625=6.25\% $$

Conditional Variance

We can calculate the conditional variance by substituting the expectation in the variance formula with the conditional expectation.

We know that:

$$ \text {Var}(\text X_1 )=\text E[\left(\text X_1-\text E(\text X_1 )\right)^2 ]=\text E(\text X_1 )^2-[\text E(\text X)]^2 $$

Now the conditional variance of \(\text X_1\) conditional on \(\text X_2\) is given by:

$$ \text {Var}(\text X_1│\text X_2=\text x_2 )=\text E(\text X_1^2 |\text X_2=x_2)-[\text E(\text X_1 |\text X_2=\text x_2 )]^2 $$

Returning to our example above, the conditional variance \(\text {Var}(\text X_1 |\text X_2=1)\) is given by:

$$ \text {Var}(\text X_1│\text X_2=1)=\text E(\text X_1^2 |\text X_2=1)-[\text E(\text X_1 |\text X_2=1)]^2 $$

Now,

$$ \text E(\text X_1 |\text X_2=1)=0.0625 $$

We need to calculate:

$$ \text E(\text X_1^2│\text X_2=1)=(-0.10)^2×0.125+0^2×0.125+0.10^2×0.75=0.00875 $$

So that

$$ \text {Var}(\text X_1│\text X_2=1)=\sigma_{(\text X_1│\text X_2=1)}^2=0.00875-[0.0625]^2=0.004844=0.484\% $$

If we wish to find the standard deviation of the returns, we just find the square root of the variance:

$$ \sigma_{(X_1│X_2=1)} =\sqrt{0.004844}=0.06960=6.96\% $$

Continuous Random Variables

Before we continue, it is essential to note that continuous random variables make use of the same concepts and methodologies as discrete random variables. The main distinguishing factor is that instead of PMFs, continuous random variables use PDFs.

The Joint PDF

The joint (bivariate) distribution function gives the probability that the pair \((\text X_1, \text X_2 )\) takes values in a stated region A. It is given by:

$$ \text P(\text a < \text X_1 < \text {b,c} < \text X_2 < \text d)=\int_\text a^\text b \int_\text c^\text d \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )\text {dx}_1 \text {dx}_2 $$

The joint pdf is always nonnegative, and the double integration yield a value of 1. That is:

$$ \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 ) \ge 0 $$

And

$$ \int_\text a^\text b \int_\text c^\text d \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )\text {dx}_1 \text {dx}_2 =1 $$

Example: Calculating the Joint Probability

Assume that the random variables \((\text X_1)\) and \((\text X_2)\) are jointly distributed as:

$$ \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\text k(\text x_1+3\text x_2 ) \quad 0 < \text x_1 < 2,0 < \text x_2 < 2 $$

Calculate the probability \(\text P(\text X_1 < 1,\text X_2 > 1)\).

Solution

We need to first calculate the value of k.

Using the principle:

$$ \int_\text a^\text b \int_\text c^\text d \text f_{\text X_1,\text X_2 } (\text x_1,\text x_2 )\text {dx}_1 \text {dx}_2 =1 $$

We have

$$ \begin{align*} \int_0^2 \int_0^2 \text k(\text x_1+3\text x_2 )\text {dx}_1 \text {dx}_2 & =\int_0^2 k{ \left[\left( \frac{1}{2} {x_1^2}+3x_1 x_2 \right)\right]}^2_{0}\text {dx}_2 =1 \\ & =\int_0^2 \text k(2+6\text x_2 )\text {dx}_2 =\text k{\left[2\text x_2+3 \text x_2^2 \right]}^2_{0}=1 \\ 16\text k &=1 \Rightarrow k=\frac {1}{16} \\ \end{align*} $$

So,

$$ \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\frac {1}{16} (\text x_1+3\text x_2 ) $$

Therefore,

$$ \text P(\text X_1 < 1,\text X_2 > 1)=\int_0^1 \int_{1}^2 \frac {1}{16} (\text x_1+3 \text x_2 )\text {dx}_1 \text {dx}_2 =0.3125 $$

Joint Cumulative Distribution Function (CDF)

The joint cumulative distribution is given by:

$$ \text F(\text X_1 < \text x_1,\text X_2 < \text x_2 )=\int_{-\infty}^{\text x_1} \int_{-\infty}^{\text x_2} \text f_{\text X_1,\text X_2} (\text t_1,\text t_2 )\text {dt}_1 \text {dt}_2 $$

Note that the lower bound of the integral can be adjusted so that it is the lower value of the interval.

Using the example above, we can calculate \(\text F( \text X_1 < 1,\text X_2 < 1)\) in a similar way as above.

The Marginal Distributions

For the continuous random the marginal distribution is given by:

$$ \text f_{\text X_1} (\text x_1 )=\int_{-\infty}^{\infty} \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )\text {dx}_2 $$

Similarly,

$$ \text f_{\text X_2} (\text x_2 )=\int_{-\infty}^{\infty} \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )\text {dx}_1 $$

Note that if we want to find the marginal distribution of \(\text X_1\) we integrate \(\text X_2\) out and vice versa.

Example: Computing the Marginal Distribution

Consider the example above. We have that

$$ \text f_{\text X_1,\text X_2} (\text x_1,\text x_2 )=\frac {1}{16} (\text x_1+3 \text x_2 ) \quad 0 < \text x_1 < 2,0 < \text x_2 < 2 $$

We wish to find the marginal distribution of \(\text X_1\). This implies that we need to integrate out \(\text X_2\). So,

$$ \begin{align*} \text f_{\text X_1} (\text x_1 ) & =\int_0^2 \frac {1}{16} ( \text x_1+3 \text x_2 )\text {dx}_2 =\frac {1}{16} { \left[\text x_1 \text x_2+\frac {3}{2} \text x_2^2 \right]} ^{2}_{0} \\ & =\frac {1}{16} \left[2 \text x_1+6 \right]=\frac {1}{8}(\text x_1+3) \\ \Rightarrow \text f_{\text X_1} (\text x_1 ) & =\frac {1}{16} \left[2 \text x_1+6 \right]=\frac {1}{8}(\text x_1+3) \\ \end{align*} $$

Note that we can calculate \(\text f_{\text X_2} (\text x_2 )\) in a similar manner.

Conditional Distributions

The conditional distribution is analogously defined as that of discrete random variables. That is:

$$ \text f_{(\text X_1│\text X_2)} (\text x_1│\text X_2=\text x_2 )=\cfrac {\text f_{\text X_1,\text X_2 } (\text x_1,\text x_2 )}{\text f_{\text X_2} (\text x_2 ) } $$

The conditional distributions are applied in the field of finance, such as risk management. For instance, we may wish to compute the conditional distribution of interest rates, \(\text X_1\), given that investors \(\text X_2\), experience a huge loss.

Independent, Identically Distributed (IID) Random Variables

A collection of random variables is independent and identically distributed (iid) if each random variable has the same probability distribution as the others and all are mutually independent.

Example:

Consider successive throws of a fair coin:

• The coin has no memory, so all the throws are “independent”.
• The probability of head vs. tail in every throw is 50:50; so the coin is equally likely and stays fair; the distribution from which every throw is drawn is  normal and stays the same, and thus each outcome is “identically distributed”

iid variables are mostly applied in time series analysis.

Mean and Variance of iid Variables

Consider the iid variables generated by the normal distribution. They are typically defined as:

$$ \text x_{\text i}^{iid} \sim \text N(\mu,\sigma^2) $$

The expected mean of these particular iid is given by:

$$ \text E \left(\sum_{\text i}^{\text n} \text X_i \right)=\sum_\text i^\text n \text E(\text X_\text i )=\sum_i^\text n \mu=\text n \mu $$

Where \(\text E(\text X_\text i )=\mu\)

The result above is valid since the variables are independent and have similar moments. Maintaining this line of thought, the variance of iid random variables is given by:

$$ \begin{align*} \text{Var}\left(\sum_\text i^{\text n} \text X_\text i \right) & =\sum_\text i^\text n \text {Var} \left(\text X_\text i \right)+2\sum_{\text j=1}^{\text n} \sum_{\text k=\text j+1}^{\text n} \text {Cov}(\text X_ \text j,\text X_\text k) \\ & =\sum_\text i^\text n \sigma^2+2\sum_{\text j=1}^\text n \sum_{\text k=\text j+1}^\text n 0 =\sum_\text i^\text n \sigma^2=\text n \sigma^2 \\ \end{align*} $$

The independence property is important because there’s a difference between the variance of the sum of multiple random variables and the variance of a multiple of a single random variable. If \(\text X_1\) and \(\text X_2\) are iid with variance \(\sigma^2\), then,

$$ \begin{align*} \text{Var}(\text X_1+\text X_2 ) & =\text {Var}(\text X_1 )+\text {Var}(\text X_2 )=\sigma^2+\sigma^2=2\sigma^2 \\ \text{Var}(\text X_1+\text X_2 ) & \neq \text{Var}(2\text X_1) \end{align*} $$

In the case of a multiple of a single variable, \(\text X_1\), with variance \(\sigma^2\),

$$ \text {Var}(2 \text X_1 )=4\text {Var}(\text X_1 )=4×\sigma^2=4\sigma^2 $$

Practice Question

A company is reviewing fire damage claims under a comprehensive business insurance policy. Let X be the portion of a claim representing damage to inventory and let Y be the portion of the same application representing damage to the rest of the property. The joint density function of X and Y is:

$$ \text f(\text x,\text y)=\begin{cases} 6[1-(\text x+\text y)], & \text x > 0,\text y > 0 \text { x} + \text y < 1 \\ 0, & {\text {elsewhere}} \end{cases} $$

What is the probability that the portion of a claim representing damage to the rest of the property is less than 0.3?

A. 0.657

B.0.450

C. 0.415

D. 0.752

The correct answer is A.

First, we should find the marginal PMF of Y:

$$ \text f_\text Y (\text y)=\int_0^{1-\text y} 6 \left[1-(\text x+\text y) \right]\partial \text x={ \left[ 6(\text x-{\frac {\text x^2}{2}}-{\text{xy}} \right]}^{1-\text y}_{0} $$

Substitute the limits as usual to get:

$$ 6\left[(1-y)-\frac{(1-y)^2}{2}-y(1-y)\right]$$

At this we can factor out \( \left(1-y\right) \) and solve what remains in the square bracket:

$$ 6(1-y) \left[1-\frac{(1-y)}{2}-y \right] =6(1-y) \left[\frac{1-y}{2} \right]$$

Of course you can cancel 2 with 6 at this point:

$$6(1-y) \left[\frac{1-y}{2} \right]=3(1-y)[1-y]=3(1-2y+y^2)=3-6y+3y^2$$

So,

$$ \text f_\text Y (\text y)=3-6\text y+3\text y^2 ,0 < \text y < 1 $$

We need \(\text P(\text Y < 0.3)\), So,

$$ \text P(\text Y < 0.3)=\int_{0}^{0.3} { (3-6\text y+3\text y^2) } \text{dy} =0.9-0.27+0.027=0.657 $$