SOA Exam FM Study Notes
Online and Printable Prep Books for Actuarial Exam FM
Exam FM is a three-hour, 35 multiple-choice questions exam designed to test your knowledge of fundamental concepts of financial mathematics. AnalystPrep has developped concise study notes focusing on exactly the learning objectives tested in the Society of Actuaries exams.
SOA Exam FM’s syllabus comprises of 8 topics and each one of them contributes a certain percentage of questions to the exam. With AnalystPrep’s concise study notes for Exam FM, you can simply read on your tablet, computer, or print each concept before jumping into the question bank portion of the platform.
Questions Answered by our Users
Satisfied Customers
Preparation Platform By Review Websites
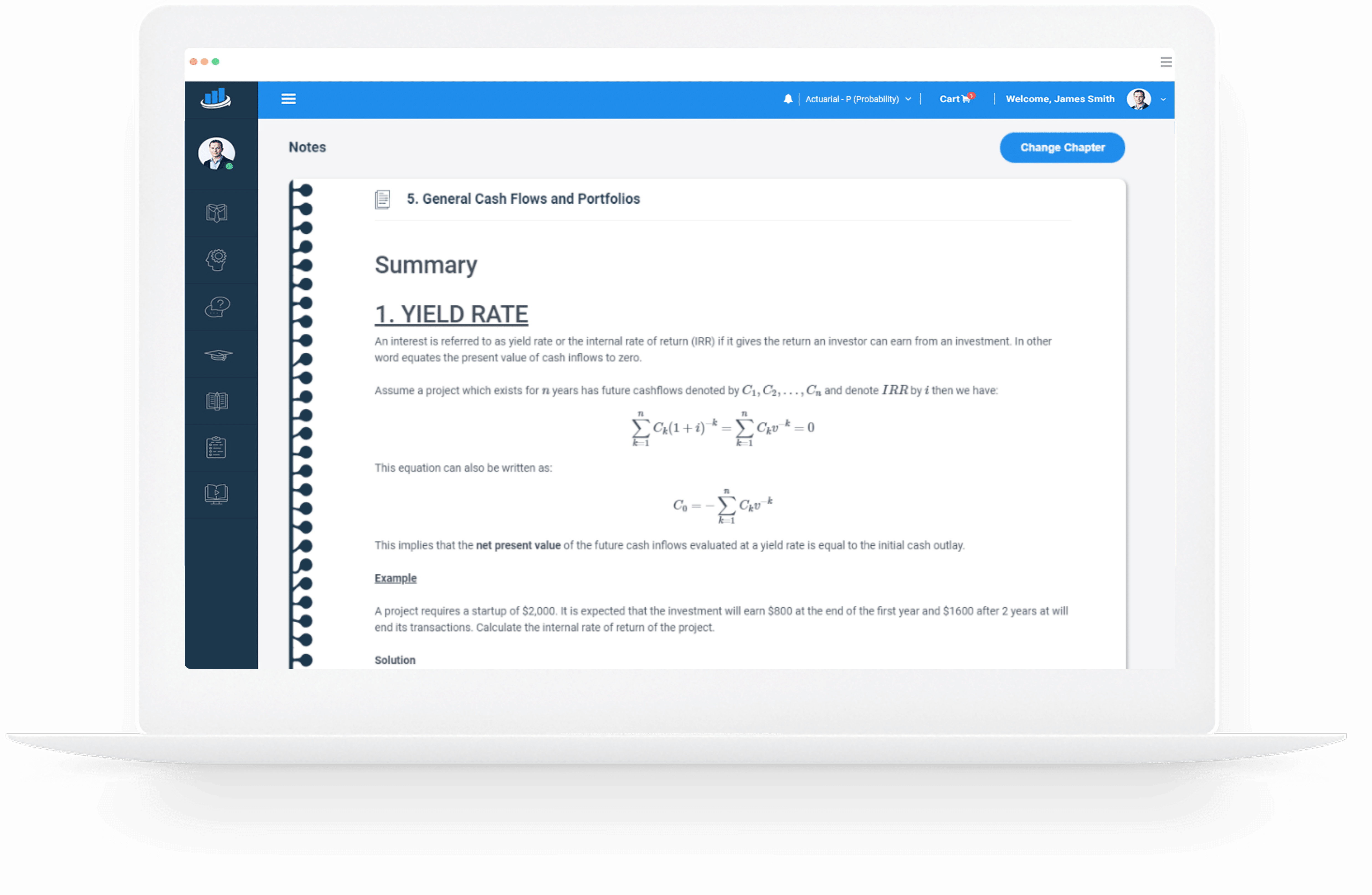
What are the Eight Topics?
The first fours topics are quite straightforward and most actuarial students should have seen the most part of this in their undergraduate degree:
- Time value of money (10-15%)
- Annuities/cash flows with non-contingent payments (15-20%)
- Loans (10-20%)
- Bonds (10-20%)
The next two topics relate mostly to the investment world and can be a little more tricky for actuarial students:
- General cash flows and portfolios (15-20%)
- Immunization (10-15%)
And the last two topics are based on interest rate and interest rate theory, but weight a bit less on the overall exam:
- Interest rate swaps (0-10%)
- Determinants of interest rates (0-10%)
Here, it is important to note that having great fundamentals in the first few topics will help you solve more easily questions from the later topics.
How Should I Study for Exam FM?
Example Learning Objective from AnalystPrep's SOA Exam P Prep Notes
Topic 2: Loans
Actuarial Exams Study Packages
Exam P (Learn + Practice Package)
$
349
/ 6-month access
- Video Lessons
- Study Notes
- Question Bank and Quizzes
- Performance Tracking Tools
- 6-Month Access
Exam FM (Learn + Practice Package)
$
349
/ 6-month access
- Video Lessons
- Study Notes
- Question Bank and Quizzes
- Performance Tools
- 6-Month Access
Unlimited Actuarial Exams Study Package
Unlimited Actuarial Exams Access
$
549
/ lifetime access
- Exams P & FM Video Lessons
- Exams P & FM Study Notes
- Question Banks and Quizzes
- Performance Tracking Tools
- Lifetime Access
- Unlimited Ask-a-Tutor Questions
Testimonials
“Thanks to your program I passed the first level of the CFA exam, as I got my results today. You guys are the best. I actually finished the exam with 45 minutes left in [the morning session] and 15 minutes left in [the afternoon session]… I couldn’t even finish with more than 10 minutes left in the AnalystPrep mock exams so your exams had the requisite difficulty level for the actual CFA exam.”
James B.
“I loved the up-to-date study materials and Question bank. If you wish to increase your chances of CFA exam success on your first attempt, I strongly recommend AnalystPrep.”
Jose Gary
“Before I came across this website, I thought I could not manage to take the CFA exam alongside my busy schedule at work. But with the up-to-date study material, there is little to worry about. The Premium package is cheaper and the questions are well answered and explained. The question bank has a wide range of examinable questions extracted from across the whole syllabus. Thank you so much for helping me pass my first CFA exam.”
Brian Masibo
“Good Day!
I cleared FRM Part I (May-2018) with 1.1.1.1. Thanks a lot to AnalystPrep and your support.
Regards,”
Aadhya Patel
“@AnalystPrep provided me with the necessary volume of questions to insure I went into test day having in-depth knowledge of every topic I would see on the exams.”
Justin T.
“Great study materials and exam-standard questions. In addition, their customer service is excellent. I couldn’t have found a better CFA exam study partner.”
Joshua Brown
“I bought their FRM Part 1 package and passed the exam. Their customer support answered all of my questions when I had problems with what was written in the curriculum. I’m planning to use them also for the FRM Part 2 exam and Level I of the CFA exam.”
Zubair Jatoi
“I bought the FRM exam premium subscription about 2 weeks ago. Very good learning tool. I contacted support a few times for technical questions and Michael was very helpful.”
Jordan Davis
