SOA Exam P Practice Questions
Get access to over 500 exam-style Probability Practice Problems
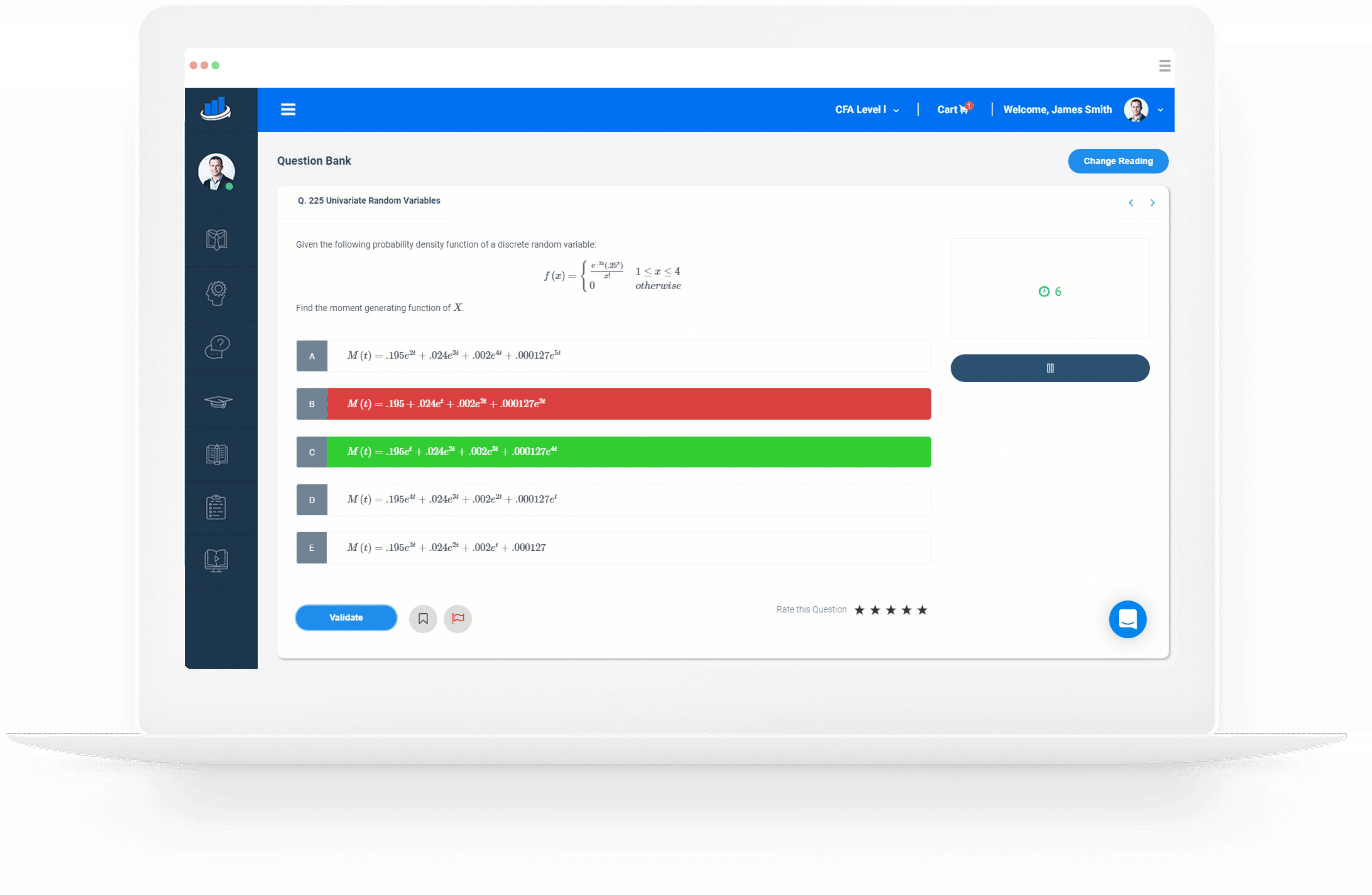
Probabilities Question Bank
At AnalystPrep, we have all you need as far as sharpening your probability wits is concerned. Our probabilities practice problems reflect the difficulty and style of the live Exam P from the Society of Actuaries. All our multiple-choice questions (from A to E – just like the actual exam) undergo regular updates to incorporate the latest review from our team of academics and actuaries.
Aside from getting up-to-date study materials, you also get access to our customizable quizzes and performance metrics tailored to help you improve your weakest areas. Also, our study notes and round-the-clock support are guaranteed to help you get ready for actuarial Exam P.
Questions Answered by our Users
Satisfied Customers
Preparation Platform By Review Websites
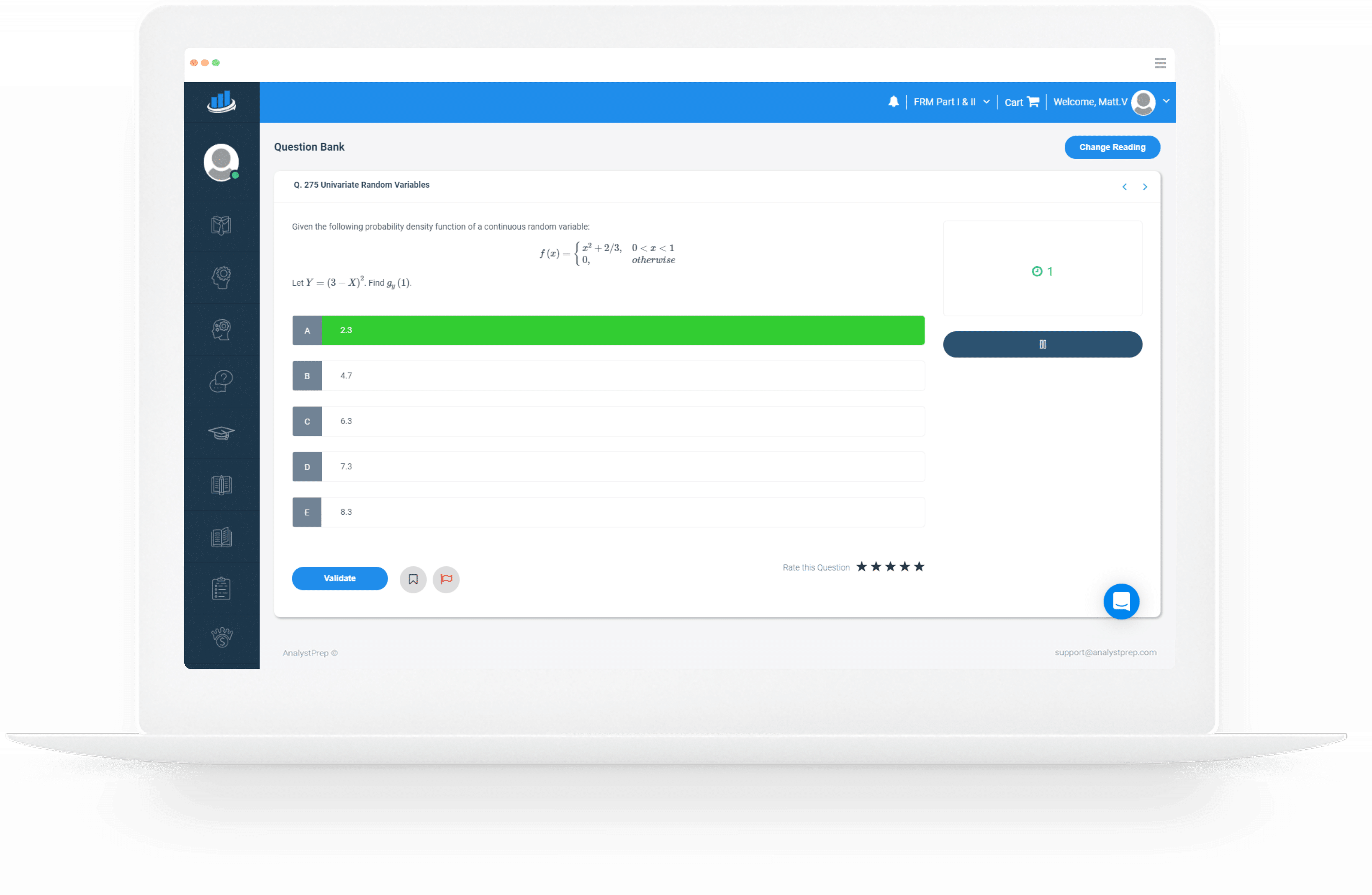
How is the Question Bank Subdivided?
AnalystPrep’s question bank for Exam P has been specifically crafted around the syllabus given by the Society of Actuaries. As such, it is subdivided into three topics:
- General probability (10-17%)
- Univariate random variables (40-47%)
- Multivariate random variables (40-47%)
However, each topics is also subdivided into each of the learning objectives given in the SOA syallbus. For example, one learning objective might read:
Calculate variance, standard deviation for conditional and marginal probability distributions.
Once you have practice with our several practice questions from a given learning objective, you can move to the next one. In doing so, you make sure no important concept is left behind.
However, a question and answer bank doesn’t mean you will revise and practice alone. Our team of expert instructors is always on hand to supplement the solutions provided with additional tips and tricks.
Free Probability Practice Problems with Answers
Question 93
General Probability (Conditional Probabilities)
60% of an insurer’s policyholders are male and 40% are female. The chance of a male having a claim is twice the chance of a female having a claim. Given a randomly selected policyholder has a claim, what’s the probability they are male?
A) 25%
B) 40%
C) 50%
D) 60%
E) 75%
The correct answer is: E)
\( P\left( Male|Claim \right) ={ P\left( Male\quad and\quad Claim \right) }/{ P\left( Claim \right) }={ .60\ast 2x }/{ \left( .60\ast 2x+.40\ast x \right) }={ 1.2x }/{ 1.6x }=\bf .75\quad or\quad 75\%\)
Question 121
General Probability (Bayes Theorem)
A test for heart disease results in a false positive 5% of the time. 25% of the population has heart disease and 20% test positive. Given a negative test, what is the probability the patient does not have heart disease?
A) 67%
B) 70%
C) 55%
D) 87%
E) 93%
The correct answer is: E)
Let event \(H\) be heart disease and event \(+\) be a positive test.
\(P\left( H’ \right) =P\left( H’|+ \right) \ast P\left( + \right) +P\left( H’|- \right) \ast \left( 1-P\left( + \right) \right) \)
\(.75 = .05 \ast .20 + x \ast \left(1-.20\right) \)
\(.75 = .01 + .80x\)
\({.74}/{.80} = x\)
\(x = .925 \quad or \quad \bf 93\%\)
Question 306
Univariate Random Variables (Cumulative Distribution Functions)
You are thinking of getting a loan for your first house, but you find out that the interest is variable and it is usually on the interval (0.09,0.15). The smallest loan amount is 100,000 and after one year its interest value would be \(V = 100,000e^R\).
Let F be the cumulative distribution of \(V\).
Determine F(v) for values of v that satisfy 0 < F(v) < 1.
A) \(\frac{100000e^{v/10000}-109,150}{9,000}\)
B) \(11.11e^{v/100,000}-0.09\)
C) \(\frac{11.11}{v}\)
D) \(11.11\bigg[ln\bigg(\frac{v}{100,000}-0.09\bigg)\bigg]\)
E) \(\frac{v}{11.11}\)
The correct answer is: D)
The distribution function of v is given by:
\begin{align*}
F(v) = P[V\leq v] & = P[100,000e^R \leq v] = P[R \leq ln(v)-ln(100,000)]\\
& = \int_{0.09}^{ln(v)-ln(100000)}\frac{1}{0.09}dr = \frac{r}{0.09}\bigg|_{0.04}^{ln(v)-ln(100,000)}\\
& = 11.11ln(v) – 11.11ln(100,000) – 1\\
& = 11.11\bigg[ln\bigg(\frac{v}{100,000}-0.09\bigg)\bigg]
\end{align*}
Question 155
Univariate Random Variables (Calculate Expected Value, Mode, Median, Percentile, and Higher Moments)
Given the following probability density function:
$$ f\left( x \right) =\begin{cases} .15 & x=1 \\ .25 & x=2 \\ .35 & x=3 \\ C & x=4 \end{cases} $$
Calculate the \({25}^{th}\) percentile of the distribution.
A) 1.5
B) 2.0
C) 2.0
D) 2.5
E) 2.7
The correct answer is: B)
The \({25}^{th}\) percentile is the value of \(x\) for which \(P\left(X \le x\right)\) is greater than or equal to .25 and \(P\left(X \ge x\right)\) is greater than or equal to .75.
\(P(X\le 2) = P(X=1)+P(X=2) = .15+.25 = .40\gt.25\)
\(P\left(X \ge 2\right) = P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right) = .25+ .35 + \left(1-.15-.25-.35\right) =.25+ .35+.25 = .85\gt.75\)
So the \({25}^{th}\) percentile is \(\bf X=2\).
Question 261
Univariate Random Variables (Sum of Independent Random Variables – Poisson Distribution)
Given that the length of time (in days) until a claim is filed with an insurance company is an exponential random variable with \(\lambda=.05\), and the length of time until the claim is paid after it is filed is an exponential random variable with \(\lambda=.10\) and is independent of the length of time until a claim is filed, find \(SD\left(X+Y\right)\).
A) 10
B) 15
C) 22
D) 22
E) 25
The correct answer is: C)
\begin{align*}
& SD=\sqrt { Var\left( X+Y \right) } =Var\left( X \right) +Var\left( Y \right) \\
& Var\left( X \right) =\frac { 1 }{ { \lambda }^{ 2 } } =\frac { 1 }{ { .05 }^{ 2 } } =400 \\
& Var\left( Y \right) =\frac { 1 }{ { \lambda }^{ 2 } } =\frac { 1 }{ { .10 }^{ 2 } } =100 \\
& Var\left(X+Y\right) = 400 + 100 = 500 \\
& SD\left(X+Y\right) = {\sqrt {500}} =\bf 22 \\ \end{align*}
Question 278
Univariate Random Variables (Apply Transformations)
Given losses at an insurance company have the following probability density function:
$$
f\left( x \right) =\begin{cases} { { x }^{ 2 }+{\frac { 2 }{ 3 }}, } & 0<x<1 \\ 0, & otherwise \end{cases}
$$
Losses are subject to a deductible of .5. Calculate the expected payout under this policy.
A) 0.17
B) 0.23
C) 0.34
B) 0.23
D) 0.46
E) 0.52
The correct answer is: A)
\begin{align*}
E\left( Y \right) &=\int _{ 0 }^{ .5 }{ 0 } \ast dx+\int _{ .5 }^{ 1 }{ \left( x-.5 \right) \left( { x }^{ 2 }+\frac { 2 }{ 3 } \right) dx } \\
& ={ \left[ 0 \right] }_{ x=0 }^{ x=.5 }+{ \left[ { x }^{ 3 }-\frac { 1 }{ 2 } { x }^{ 2 }+\frac { 2 }{ 3 } x-\frac { 1 }{ 3 } \right] }_{ x=.5 }^{ x=1 }=\bf .17 \\ \end{align*}
Question 336
Multivariate Random Variables (Joint Probability Functions)
Let X represent the age of an insured automobile involved in an accident. Let Y represent the length of time the insurance contract has been in place at the time of the accident.
X and Y have joint probability density function
\(f(x,y)=\begin{cases} \cfrac { 1 }{ 64 } (10-x{ y }^{ 2 })\quad \quad 2\le x\le 10,\quad 0\le y\le 1 \\ 0\quad \quad \quad \quad \text{otherwise}\end{cases}\)
Calculate the expected length of time the contract has been in place for an insured automobile involved in an accident.
A) 0.4375
B) 0.5500
C) 0.1420
D) 0.2010
E) 0.8185
The correct answer is: A)
The marginal density of Y is given by:
\({ f }_{ Y }(y)=\int _{ 2 }^{ 10 }{ \cfrac { 1 }{ 64 } (10-x{ y }^{ 2 })\partial x=\cfrac { 1 }{ 64 } (10x-\cfrac { { x }^{ 2 }{ y }^{ 2 } }{ 2 } )|_{ 2 }^{ 10 }=\cfrac { 1 }{ 64 } (80-48{ y }^{ 2 }) }\)
Then,
\(E(Y)=\int _{ 0 }^{ 1 }{ y\times \cfrac { 1 }{ 64 } (80-48{ y }^{ 2 })\partial y= } \cfrac { 1 }{ 64 } (40{ y }^{ 2 }-12{ y }^{ 4 })|_{ 0 }^{ 1 }=\cfrac { 1 }{ 64 } (40-12)=\cfrac { 28 }{ 64 } =\cfrac { 7 }{ 16 }\)
Question 560
Multivariate Random Variables (Moment Generating Functions)
Let \(X_1,X_2\) be independent random variables with the following pmf
$$ f\left( x \right) =\begin{cases} \frac { 1 }{ 4 } & x=4 \\ \frac { 1 }{ 2 } & x=5 \\ \frac { 1 }{ 4 } & x=6 \\ 0, & otherwise \end{cases}
$$
Let \(Y = X_1 + X_2\).Find \(Var\left(Y\right)\) using moment generating function technique.
A) 1
B) 5
C) 10
D) 15
E) 20
The correct answer is: A)
Find \(E \left(Y\right)={ M }_{ Y }^{ \prime }\left( 0 \right) \) and \(E \left(Y^2\right)={ M }_{ Y }^{ \prime\prime }\left( 0 \right) .\)
\({ M }_{ { X }_{ 1 } }\left( t \right) =E\left( { e }^{ t{ X }_{ 1 } } \right) =\frac { 1 }{ 4 } \ast { e }^{ 4t }+\frac { 1 }{ 2 } \ast { e }^{ 5t }+\frac { 1 }{ 4 } \ast { e }^{ 6t }.\)
\( { M }_{ { X }_{ 2 } }\left( t \right) = { M }_{ { X }_{ 1 } }\left( t \right) \).
\( { M }_{ { Y } }\left( t \right) ={ M }_{ { X }_{ 1 } }\left( t \right) { M }_{ { X }_{ 2 } }\left( t \right)=\left( \frac { 1 }{ 4 } \ast { e }^{ 4t }+\frac { 1 }{ 2 } \ast { e }^{ 5t }+\frac { 1 }{ 4 } \ast { e }^{ 6t } \right) \left( \frac { 1 }{ 4 } \ast { e }^{ 4t }+\frac { 1 }{ 2 } \ast { e }^{ 5t }+\frac { 1 }{ 4 } \ast { e }^{ 6t } \right) =\frac { 1 }{ 16 } { e }^{ 8t }+\frac { 1 }{ 4 } { e }^{ 9t }+\frac { 3 }{ 8 } { e }^{ 10t }+\frac { 1 }{ 4 } { e }^{ 11t }+\frac { 1 }{ 16 } { e }^{ 12t }. \)
\({ M }_{ Y }^{ \prime }\left( t \right) =\frac { 1 }{ 2 } { e }^{ 8t }+\frac { 9 }{ 4 } { e }^{ 9t }+\frac { 15 }{ 4 } { e }^{ 10t }+\frac { 11 }{ 4 } { e }^{ 11t }+\frac { 3 }{ 4 } { e }^{ 12t }\)<br><br>
\(E\left( Y \right) ={ M }_{ Y }^{ \prime }\left( 0 \right) =\frac { 1 }{ 2 } +\frac { 9 }{ 4 } +\frac { 15 }{ 4 } +\frac { 11 }{ 4 } +\frac { 3 }{ 4 } =10\)
\({ M }_{ Y }^{ \prime \prime }\left( t \right) =4{ e }^{ 8t }+\frac { 81 }{ 4 } { e }^{ 9t }+\frac { 75 }{ 2 } { e }^{ 10t }+\frac { 121 }{ 4 } { e }^{ 11t }+9{ e }^{ 12t }\)
\(E\left(Y^2\right)=M_Y^{\prime \prime} \left(0\right)=101\)
\(Var \left(Y \right)=E\left(Y^2\right)-E\left(Y\right) \ast E\left(Y\right)=101-100=1\)
Question 454
Multivariate Random Variables (Transformation of Jointly Distributed Random Variables)
Let \(Y_1 < Y_2 < \cdots < Y_6\) be the order statistics of a random sample of size 6 from a distribution \(X\) with pdf \(f(x)=3x^2, 0 \le x \le 1\). Find the pdf of \(Y_6\).
A) \(g_1 (y)=3y^2,0 \le y \le 1\)
B) \(g_1 (y)=18y^{17},0 \le y \le 1\)
C) \(g_1 (y)=17y^{18},0 \le y \le 1\)
D) \(g_1 (y)=3y^{27},0 \le y \le 1\)
E) \(g_1 (y)=18y^2 (1-y^3)^5,0 \le y \le 1\)
The correct answer is: E)
The pdf of \(X\) is \(F(x)=x^3,0 \le x \le 1\).
\(g_6 (y)={\frac {6!}{(6-1)!}} (1-F(y))^5 f(y)=18y^{2}(1-y^3)^5,0 \le y \le 1\).




