GMAT® Practice Questions
Get Access to 1,000 Exam-Style Questions
What is the GMAT Quantitative Reasoning Questions Exam Structure?
The quantitative reasoning section tests your numerical literacy and mathematical abilities, such as solving quantitative problems and interpreting graphical data. It consists of 31 multiple choice questions, which should take 62 minutes (2 minutes per question) to be completed.
The quantitative reasoning section of questions consists of data sufficiency and problem-solving questions.
1. Data Sufficiency Questions
Each Data sufficiency question is made up of a question and two statements. To answer a question, one should first identify the statement that provides information relevant to the question, and then eliminate all the other possible answers by using math knowledge and other everyday facts. There will be 14 to 15 questions on data sufficiency in each quantitative section.
2. Problem-solving Questions
Each Problem-solving question includes a question section and five possible answers to choose from. The questions are designed to assess your use of logic and analytical reasoning to answer quantitative problems.
What are the Skills and Strategies to Excel in Quantitative Reasoning Questions?
Math Skills
Quantitative Reasoning questions call for the application of math knowledge to solving problems. Such mathematical skills include:
- Basic arithmetic including fractions, integers, powers and roots, and statistics and probability.
- Algebraic topics such as variables, functions, and solving equations.
- Word problems such as algebraic and geometric principles and blending arithmetic used to solve problems.
- Geometry, particularly geometrical objects such as triangles, circles, quadrilaterals, solids, cylinders, and coordinate geometry.
Essential Strategies in Problem Solving Questions
- Always check your onscreen timer. Apply caution while solving questions but don’t waste too much time verifying answers; strive to complete a given section.
- If you find a question difficult or time-consuming, try to eliminate answer choices that might be outrightly wrong and select your best choice from the remaining ones.
- Study each question in depth to ascertain what is being asked. For example, you may need to come up with some equations.
- Solve the questions by writing to limit errors. An erasable tablet will be provided at the test center.
- For the data sufficiency questions, ascertain whether the question requires only one value or a range of values. Moreover, avoid unnecessary assumptions about geometrical figures, as they are not usually drawn to scale.
- Go through the answer choices before answering a question to get the gist of what kind of answer choice structure you are required to present. Moreover, some questions require simple approximation presentations, which may require little mental activity rather than long computations.
Questions Answered by our Users
Satisfied Customers
Preparation Platform By Review Websites
Some Free Exam-style GMAT Practice Questions offered by AnalystPrep
GMAT Quantitative Problems
Question 1
Division & Factoring
When a number \(b\) is divided by \(a\), the remainder is 12. Given that \(\frac{b}{a}=7.15\), what is the value of a?
A) \(72\)
B) \(90\)
C) \(80\)
D) \(82\)
E) \(78\)
The correct answer is: C)
The result 7.15 due to division gives us the quotient 7 and the remainder 0.15. Therefore,
\(\frac{12}{a} =0.15\) implying that \(a=\frac{12}{0.15}=80\).
Question 2
Descriptive Statistics
Dre has seven French tests this semester that is each scored out of a maximum of 100 points. If his average score on the first five tests was 87, what is the minimum score he could get on the sixth test and still be able to maintain his 87 average through all seven tests?
A) 74
B) 77
C) 80
D) 85
E) 87
The correct answer is: A)
If the average score on Dre’s first five tests is 87, the sum of the first 5 scores is \(5 × 87 = 435\).
To maintain a score of 87 for all 7 tests, the total score required would be \(7 × 87 = 609\).
The maximum score Dre could get on the seventh test would be 100, so \(609 – 435 – 100 = 74\) would be the minimum score he could get on test 6 and still maintain his 87 point score average.
Question 3
Linear Algebra
Scott began losing weight at a constant rate five months ago and today weighs 25 pounds less than he weighed then. Concurrently, his brother Karl has also been losing weight at three times the rate of Scott. If Karl weighed the same weight two months ago that Scott is today, and the two brothers weigh a combined 450 pounds today, what was Scott’s weight five months ago?
A) 215
B) 225
C) 260
D) 265
E) 285
weight 5 months ago.Scott’s weight loss rate is given as 5 pounds per month, and hence he has
lost a total of \(5×5=25\) pounds over 5 months.
So, Scott’s weight today \(= s−25\).
Karl’s weight loss rate is three times that of Scott, i.e., 15 pounds per month.
So, Karl has lost a total of \(15×5=75\) pounds over 5 months.
Karl’s weight today = k−75.
Given, their combined weight today is 450 pounds:
$$\begin{align*}s−25+k−75&=450\\
s+k&=550\end{align*}$$
(1)
From the problem, we know that Karl weighed the same as Scott does today
2 months ago. Thus, Karl’s weight 2 months ago was \(k−3(15)=k−45\), because
he loses 15 pounds each month.
Given:
$$\begin{align*}s−25&=k−45\\
s−k&=-20\end{align*}$$
From this:
$$s=k-20$$
(2)
Now, plugging (2) into (1):
$$\begin{align*}k-20+k&=550\\
2k-20&=550\\
2k&=570\\
k&=285\end{align*}$$
And from (2):
$$\begin{align*}s&=550-285\\
s&=265\end{align*}$$
Question 4
Basic Quadratics
If \(y=x^2 +mx + 48\) has x-intercepts (a, 0) and (b, 0), where a and b are integers, what is the least possible value of m?
A) -14
B) -21
C) -44
D) -49
E) -50
The correct answer is: D)
We know that ab=48 and a+b=m, so we just need to find all the possible combinations of a and b. We have the possible sets (1, 48), (2, 24), (3, 16), (4, 12), (6, 8), and their negative counterparts.
To find the value of m, we need to find the lowest sum of each pair of numbers.
It would be (-1, -48) whose sum is -49.
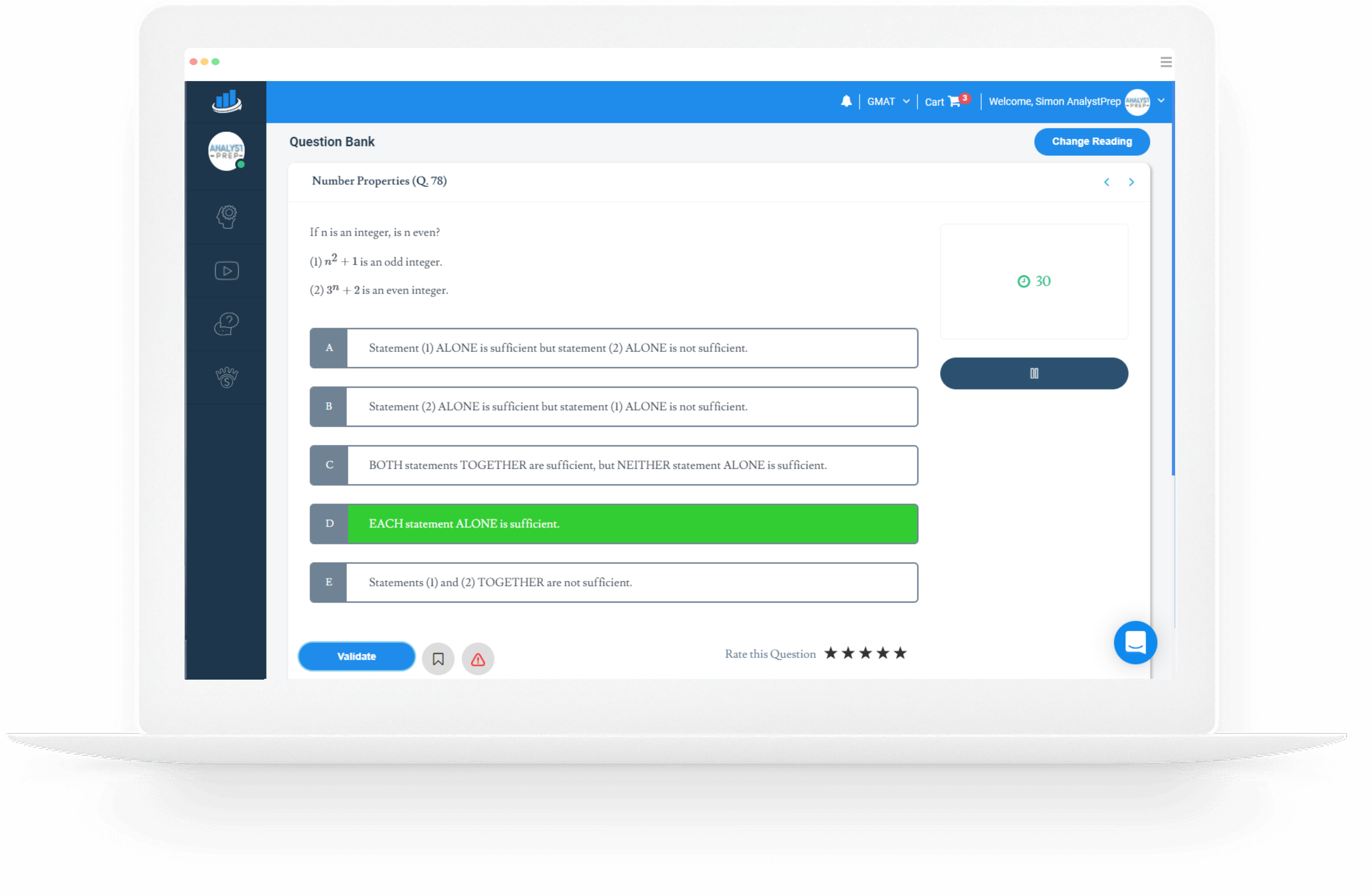
Question 5
Functions & Symbols
For any two integers m and n, range(m, n) denotes the difference in the values of m and n. For example, range(3, 6) = 3. For the integers c and d, what is the value of range(c, d)?
(1) range(c, 6) = 20
(2) range(d, 15) = 5
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: E)
(1) This statement allows for two possible values of c, 4 or 8 and provides no information about d; NOT sufficient.
(2) This statement allows for two possible values of d, 10 or 20 and provides no information about c; NOT sufficient.
(Together) There are still multiple possible differences for range(c, d); NOT sufficient.
The correct answer is E; both statements together are still not sufficient.
Question 6
Algebra
A rectangular tennis court is divided into six sections with a net splitting the court into two halves at the midpoint of its length. Each half has three equal sections consisting of a single large section and two equal smaller sections exactly half the size of the large section. If the length of the entire court is 24 meters, and the area of one of the smaller sections is 24 square meters, what is the width of the entire court?
A) 4 meters.
B) 6 meters.
C) 8 meters.
D) 12 meters.
E) 24 meters.
The correct answer is: C)
If the area of two smaller sections of one half of the court is equal to half of that half of the court’s area, then \(24 = \frac{1}{2} × \frac{1}{2}lw\)
Since the length of half of the court is 12 meters, solve for \(w\) using the equation as \(24 = \frac{1}{2} × \frac{1}{2}(12)w\)
Multiply the full equation by 4 to find that \(96 = 12w\) and divide by 12 to find that \(8 = w\).
Question 7
Rates and Work
Operating at the same time at their respective constant rates, Misha and Petro can repair 100 widgets in \(q\) hours. Working by himself at his constant rate, Misha repairs 100 widgets in \(w\) hours. In terms of \(q\) and \(w\), how many hours does it take Petro, working alone at his constant rate, to repair 100 widgets?
A) \(\frac {qw}{w-q}\).
B) \(\frac {qw}{q-w}\).
C) \(\frac {q}{w+q}\).
D) \(\frac {w}{w-q}\).
E) \(\frac {q}{q-w}\).
The correct answer is: A)
Use the combined time formula where combined time = \(\frac{time A × time B}{time A + time B}\), where time for Misha = \(w\), combined time = \(q\) and time for Petro = \(x\).
Therefore, \( q = \frac{xw}{x + w}\).
Multiply the equation by \(x + w\) to find \(qx + qw = xw\).
Subtract by \(qx\) and factor \(x\) to find that \(qw = x(w – q)\).
Divide by \(w – q\) to find that \(\frac{qw}{w – q} = x\).
GMAT® Focus Prep Packages
GMAT Focus Complete Course
$
39
/ month
- Conceptual Video Lessons
- Quantitative Practice Problems
- Verbal Practice Problems
- Data Insight Practice Problems
- Customizable Quizzes
- Performance Tracking Tools