SOA Exam P Study Notes
Online and Printable Prep Books for Actuarial Exams
Exam P is a three–hour multiple–choice examination designed to test your knowledge of fundamental probability tools using for assessing risk. AnalystPrep has developped concise study notes focusing on exactly the learning objectives tested in the Society of Actuaries exam.
There are three main topics in the exam and each topics has a multitude of different learning objectives. With AnalystPrep’s concise study notes for Exam P, you can simply read on your tablet, computer, or print each concept before jumping into the question bank portion of the platform.
Questions Answered by our Users
Satisfied Customers
Preparation Platform By Review Websites
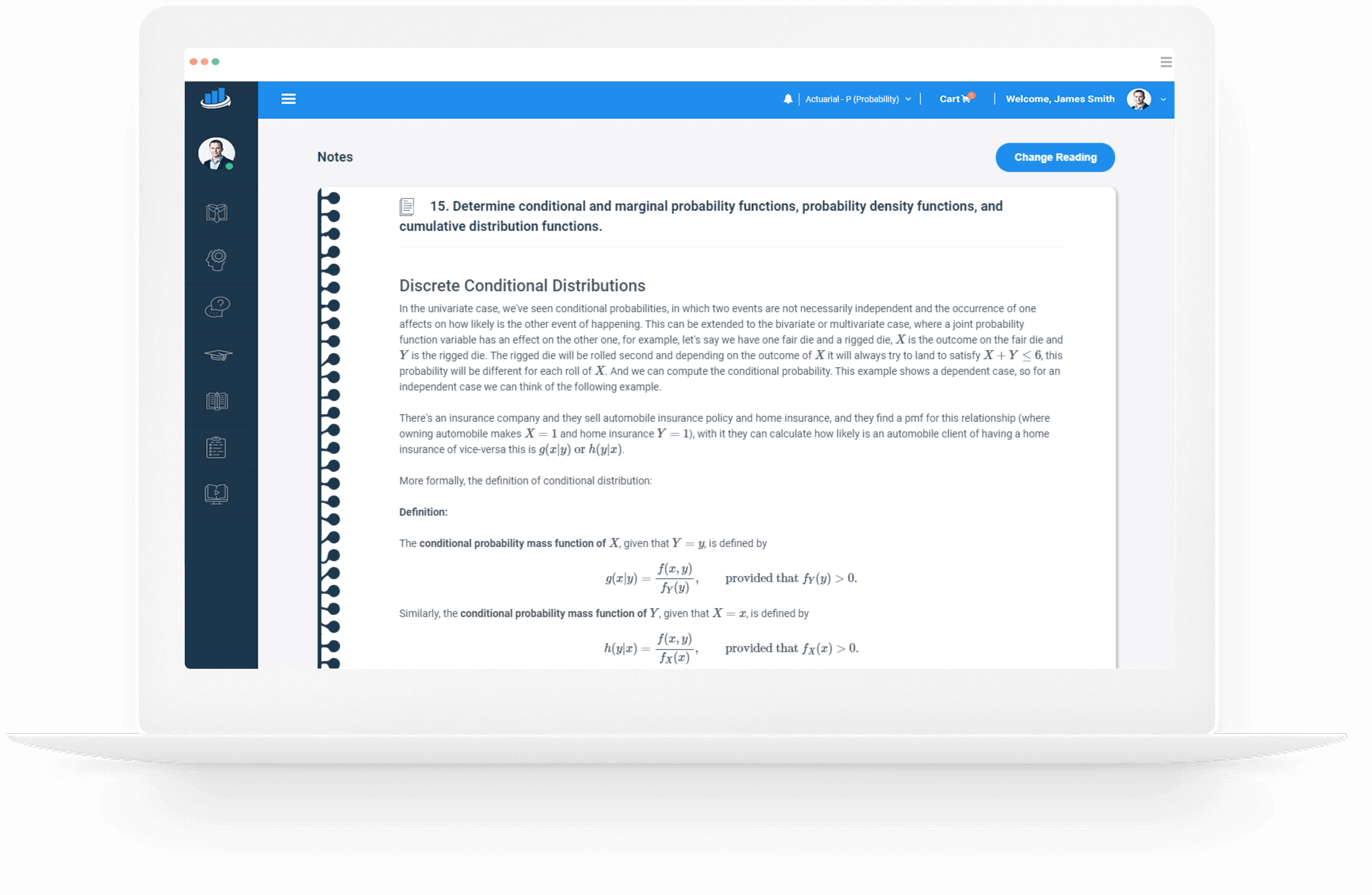
What are the Three Topics?
General probability accounts for the smallest portion of the overall exam – usually 10 to 17 percent.
The objective of general probability is to equip you with an understanding of basic probability concepts such as:
- Define and calculate conditional probabilities.
- State Bayes theorem and the law of total probability.
- Calculate the probabilities of mutually exclusive events.
- Use combinatorics such as combinations and permutations to calculate probability.
- etc.
The univariate random variables topic accounts for between 40 and 47 percent of the whole test.
The learning objective is for you to get a grip on important concepts of discrete and continuous univariate random variables and how they can be applied in different scenarios. The following should be at your fingertips by the time you’re through with this topic:
- Applications of transformations.
- Random variables, probability and probability density functions, and cumulative distribution functions.
- Variance, standard deviation, and coefficient of variation – what each one of them means and how to find them using the given information.
- etc.
Just like univariate random variables, multivariate random variables can make 40-47% of the whole test. The two account for the largest portion of Exam P. It serves the purpose of developing your knowledge in key concepts involving multivariate random variables – and that also includes the bivariate normal. Here’s what is expected of you as a learner by the end of this topic:
- Explain and apply joint moment generating functions.
- Find moments for conditional, joint, and marginal random variables..
- Evaluate standard deviation and variance specifically for marginal and conditional probability distributions.
- etc.
This isn't a Sprint
Example Learning Objective from AnalystPrep's SOA Exam P Prep Notes
Topic 2: Univariate Random Variables. Learning objective d) Explain and calculate variance, standard deviation, and coefficient of variation.
The variance of a discrete random variable is the sum of the square of all the values the variable can take times the probability of that value occurring minus the sum of all the values the variable can take times the probability of that value occurring squared as shown in the formula below:
$$ Var\left( X \right) =\sum { { x }^{ 2 }p\left( x \right) -{ \left[ \sum { { x }p\left( x \right) } \right] }^{ 2 } } $$
Or written in another way, as a function of \(E(X)\), then:
$$ Var\left( X \right) =E\left( { X }^{ 2 } \right) -E{ \left( X \right) }^{ 2 } $$
Often \(E(X)\) is written as \(\mu\) and therefore variance can also be shown as in the formula below:
$$ Var\left( X \right) =\sum { { \left( x-\mu \right) }^{ 2 }p\left( x \right) } $$
Example
Given the experiment of rolling a single die, calculate \(Var(X)\).
\( E(X) = 1 \ast ({1}/{6})+2 \ast ({1}/{6})+ 3 \ast ({1}/{6})+ 4 \ast ({1}/{6})+ 5 \ast ({1}/{6})+ 6 \ast ({1}/{6}) = 3.5 \)
\( E(X^2) = 1 \ast ({1}/{6})+2^2 \ast ({1}/{6})+ 3^2 \ast ({1}/{6})+ 4^2 \ast ({1}/{6})+ 5^2 \ast ({1}/{6})+ 6^2 \ast ({1}/{6}) = {91}/{6} \)
\( Var \left(X\right) = \left(91/6 \right) – \left(3.5 \right)^2 = {35}/{12} = 2.92 \)
We could also calculate \(Var(X)\) as:
\( E \left(X \right) = \mu =3.5 \)
\begin{align*}
Var \left(X \right) = & (1-3.5)^2 \ast (1/6) + (2-3.5)^2 \ast (1/6)+(3-3.5)^2 \ast (1/6)+(4-3.5)^2 \ast (1/6)+ \\
& (5-3.5)^2 \ast (1/6)+(6-3.5)^2 \ast (1/6) = 2.92 \\
\end{align*}
The variance of a continuous random variable is shown in the formula below:
$$ Var\left( X \right) =\int _{ -\infty }^{ \infty }{ { x }^{ 2 }f\left( x \right) dx } -{ \left[ \int _{ -\infty }^{ \infty }{ { x }f\left( x \right) dx } \right] }^{ 2 } $$
where \(f(x)\) is the probability density function of \(x\).
As in the discrete case, it can also be written as:
$$ Var\left( X \right) =E\left( { X }^{ 2 } \right) -E{ \left( X \right) }^{ 2 } $$
And also,
$$ Var\left( X \right) =\int _{ -\infty }^{ \infty }{ { \left( x-\mu \right) }^{ 2 }f\left( x \right) dx } $$
Example
Given the following probability density function of a continuous random variable:
$$ f\left( x \right) =\begin{cases} \frac { x }{ 2 } , & 0 < x < 2 \\ 0, & otherwise \end{cases} $$
Calculate \(Var(X)\).
$$
\begin{align*}
& E\left( X \right) =\int _{ -\infty }^{ \infty }{ xf\left( x \right) dx= } \int _{ 0 }^{ 2 }{ x\ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 3 } }{ 6 } \right] }_{ x=0 }^{ x=2 }=\frac { 8 }{ 6 } =\frac { 4 }{ 3 } \\
& E\left( X^2 \right) =\int _{ -\infty }^{ \infty }{ x^2 f\left( x \right) dx= } \int _{ 0 }^{ 2 }{ x^2 \ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 4 } }{ 8 } \right] }_{ x=0 }^{ x=2 }=2 \\
& Var \left(X \right) = 2 – {\left({4}/{3}\right)}^ 2 = {2}/{9} \\
\end{align*}
$$
Or,
$$ Var\left( X \right) =\int _{ -\infty }^{ \infty }{ { \left( x-\mu \right) }^{ 2 }f\left( x \right) dx= } \int _{ 0 }^{ 2 }{ { \left( x-\frac { 4 }{ 3 } \right) }^{ 2 }\ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 4 } }{ 8 } -\frac { 4 }{ 9 } { x }^{ 3 }+\frac { 4 }{ 9 } { x }^{ 2 } \right] }_{ x=0 }^{ x=2 }=\frac { 2 }{ 9 } $$
The standard deviation, often written as \(\sigma\) , of either a discrete or continuous random variable can be defined as:
$$ S.D.\left( X \right) =\sigma =\sqrt { Var\left( X \right) } $$
The coefficient of variation of a random variable can be defined as the standard deviation divided by the mean (or expected value) of \(X\) as shown in the formula below:
$$ C.V.= {\frac {\sigma}{\mu}} $$
The variance of \(X\) is sometimes often referred to as the second moment of \(X\) about the mean.
The third moment of \(X\) is referred to as the skewness and the fourth moment is called kurtosis.
In general, the mth moment of \(X\) can be calculated from the following formula:
$$ mth\quad moment\left( X \right) =\int _{ -\infty }^{ \infty }{ { \left( x-\mu \right) }^{ m }f\left( x \right)dx } $$
Example
Given the following probability density function of a continuous random variable:
$$ f\left( x \right) =\begin{cases} \frac { x }{ 2 } , & 0 < x < 2 \\ 0, & otherwise \end{cases} $$
Calculate the skewness.
\( \begin{align*}
\mu & =\int _{ -\infty }^{ \infty }{ xf\left( x \right) dx= } \int _{ 0 }^{ 2 }{ x\ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 3 } }{ 6 } \right] }_{ x=0 }^{ x=2 }=\frac { 8 }{ 6 } =\frac { 4 }{ 3 } \\
Skew\left( X \right) & =\int _{ -\infty }^{ \infty }{ { \left( x-\mu \right) }^{ 3 }f\left( x \right) dx= } \int _{ 0 }^{ 2 }{ { \left( x-\frac { 4 }{ 3 } \right) }^{ 3 }\ast \frac { x }{ 2 } \ast dx } \\
& =\int _{ 0 }^{ 2 }{ \left( \frac { { x }^{ 4 } }{ 2 } -2{ x }^{ 3 }+\frac { 8{ x }^{ 2 } }{ 3 } -\frac { 32x }{ 27 } \right) dx={ \left[ \frac { { x }^{ 5 } }{ 10 } -\frac { { x }^{ 4 } }{ 2 } +\frac { 8{ x }^{ 3 } }{ 9 } -\frac { 16{ x }^{ 2 } }{ 27 } \right] }_{ x=0 }^{ x=2 }=-{ 8 }/{ 135 } }
\end{align*}
\)
Binomial (and Bernoulli)
An experiment is performed with probability of success, \(p\), and failure, \(1-p\), and the experiment is performed \(n\) times.
$$
\begin{align*}
& p\left( x \right) =\left( \begin{matrix} n \\ x \end{matrix} \right) { p }^{ X }{ \left( 1-p \right) }^{ n-x } \\
& E\left( X \right) =np \\
& Var\left( X \right) =np\left( 1-p \right) \\
\end{align*}
$$
A Bernoulli random variable is the special case of a binomial random variable where the experiment is performed only once.
Negative Binomial
Given an experiment that is performed \(X\) number of times until a total of \(r\) successes occur, then
$$
\begin{align*}
& p\left( x \right) =\left( \begin{matrix} x-1 \\ r-1 \end{matrix} \right) { \left( 1-p \right) }^{ x-r }{ p }^{ r } \\
& E\left( X \right) =\frac { r }{ p } \\
& Var\left( X \right) ={ r\left( 1-p \right) }/{ p^{ 2 } } \\
\end{align*}
$$
Geometric
Given an experiment that is performed \(X\) number of times until a success occurs, with the probability of a success on each trial being equal to \(p\), then
$$ \begin{align*}
& p\left(x \right)=\left(1-p \right)^\left(x-1\right) p \\
& E \left(X \right)={1}/{p} \\
& Var\left(X \right)={\left(1-p \right)}/{p^2} \\
\end{align*}
$$
Hypergeometric
$$ \begin{align*}
& p\left( x \right) =\frac { \left( \begin{matrix} M \\ x \end{matrix} \right) \left( \begin{matrix} N-M \\ n-x \end{matrix} \right) }{ \left( \begin{matrix} N \\ n \end{matrix} \right) } \\
& E\left(X \right)={\frac {nm}{N}} \\
& Var \left(X \right)={nm \left(N-M \right)\left(N-n\right)}/{N^2 \left(N-1 \right)} \\
\end{align*}
$$
Poisson
A Poisson random variable can be described as the number of events occurring in a fixed time period if the events occur at a known constant rate,\(\lambda\).
$$ \begin{align*}
& p \left(x \right)={\frac {{e}^{-\lambda} {\lambda}^{x}}{x!}} \\
& E(X) = \lambda \\
& Var \left(X \right) = \lambda \\
\end{align*}
$$
Uniform – Discrete
Given an experiment in which outcomes are all equally likely
$$ \begin{align*}
& p \left(x \right)={\frac {1}{b-a+1}} \\
& E \left(X \right)={\frac {b+a}{2}} \\
& Var \left(X \right)={\frac {\left(b-a+2 \right)\left(b-a\right)}{12}} \\
\end{align*}
$$
Uniform – Continuous
$$ \begin{align*}
& f\left(x \right)={\frac {1}{b-a}} \\
& E\left(X \right)={\frac {b+a}{2}} \\
& Var \left(X \right)={\frac {{\left(b-a \right)}^2}{12}} \\
\end{align*}
$$
Exponential
$$ \begin{align*}
& f\left(x \right)= {{\lambda}e}^{-{\lambda} x} \\
& E\left(X \right)={\frac {1}{\lambda}} \\
& Var \left(X \right)={\frac {1}{{\lambda}^2}} \\
\end{align*}
$$
Gamma
$$ \begin{align*}
& f\left( x \right) =\frac { {{\lambda}e}^{-{\lambda} x}{ \left( {\lambda} x \right) }^{ \alpha -1 } }{ \Gamma \left( \alpha \right) } \\
& where\quad { \Gamma \left( \alpha \right) }=\int _{ 0 }^{ \infty }{ { e }^{ -y }{ y }^{ \alpha -1 }dy } \\
& E \left(X \right)={\frac {\alpha}{\lambda}} \\
& Var \left(X \right)={\frac {\alpha}{\lambda^2} } \\
\end{align*}
$$
Normal
$$ \begin{align*}
& f\left( x \right) =\frac { 1 }{ \sigma \sqrt { 2\pi } } { e }^{ -.5{ \left( \frac { x-\mu }{ \sigma } \right) }^{ 2 } }
\\
& E \left(X \right)= \mu \\
& Var \left(X\right)= \sigma \\
\end{align*}
$$
The standard normal distribution has \(E(X) = 0\) and \(Var(X) = 1\).
Actuarial Exams Study Packages
Exam P (Learn + Practice Package)
$
349
/ 6-month access
- Video Lessons
- Study Notes
- Question Bank and Quizzes
- Performance Tracking Tools
- 6-Month Access
Exam FM (Learn + Practice Package)
$
349
/ 6-month access
- Video Lessons
- Online Study Notes
- Online Question Bank and Quizzes
- Performance Tools
- 6-Month Access
Unlimited Actuarial Exams Study Package
Unlimited Actuarial Exams Access
$
549
/ lifetime access
- Exams P & FM Video Lessons
- Study Notes
- Question Banks and Quizzes
- Performance Tracking Tools
- Lifetime Access
- Unlimited Ask-a-Tutor Questions













