No-Arbitrage Values of Options
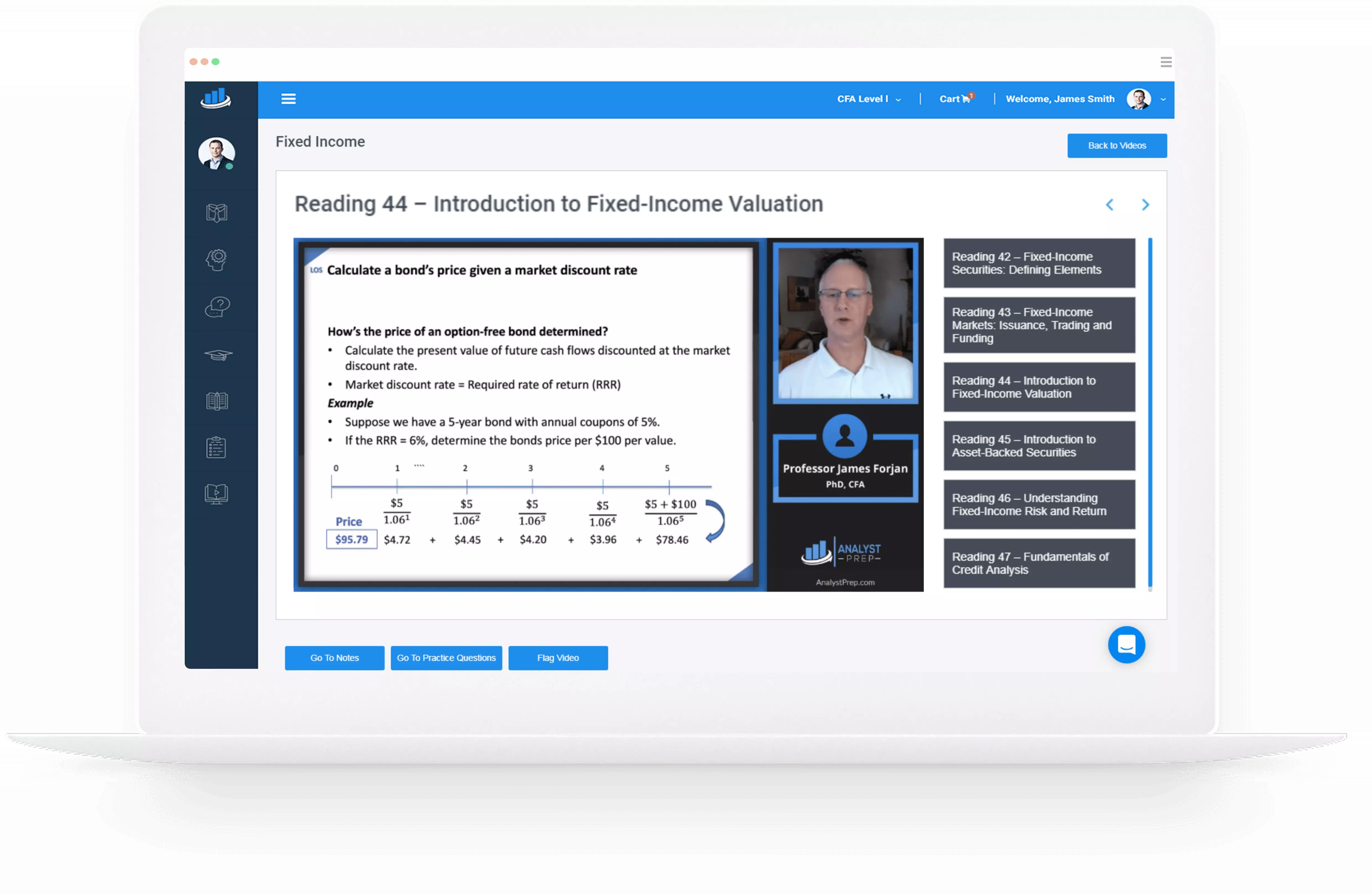
Valuing European Options A European option is an option that can only be exercised at expiry. Let’s consider a simple example to better illustrate the concept. Example: The Value of a European Option Consider a stock with an initial price…
Binomial Option Valuation Model
Contingent Claims A contingent claim is a derivative contract that gives the owner the right but not the obligation to receive a future payoff that depends on the value of the underlying asset. Call and put options are examples of…
Implied Volatility
We have seen that both the BSM model and Black model require the parameter, \(\sigma\) which is the volatility of the underlying asset price. However, future volatility cannot be observed directly from the market but rather estimated. One way of…
Delta Hedging
Delta hedging involves adding up the deltas of the individual assets and options making up a portfolio. A delta hedged portfolio is one for which the weighted sums of deltas of individual assets is zero. A position with a zero…
Option Greeks
The Greeks are a group of mathematical derivatives applied to help manage or understand portfolio risks. They include delta, gamma, Theta, Vega, and rho. Delta Delta is the rate of change of the option’s price with respect to a given…
Black Option Valuation Model
The black option valuation model is a modified version of the BSM model used for options on underlying securities that are costless to carry, including options on futures and forward contracts. Similar to the BSM model, the black model assumes…
Expectations Valuation Approach
One-Step Binomial Tree The idea that a hedged portfolio returns the risk-free rate can determine the initial value of a call or put. The expectations approach calculates the values of the option by taking the present value of the expected…
Valuation of an Interest Rate Option (2022 curriculum)
Interest rate options are options with an interest rate as the underlying. A call option on interest rates has a positive payoff when the current spot rate is greater than the exercise rate. $$\text{Call option payoff}=\text{Notional Amount}\times[\text{Max}(\text{Current spot rate}-\text{Exercise rate,…