Valuation of an Interest Rate Option (2022 curriculum)

Interest rate options are options with an interest rate as the underlying. A call option on interest rates has a positive payoff when the current spot rate is greater than the exercise rate.

$$\text{Call option payoff}=\text{Notional Amount}\times[\text{Max}(\text{Current spot rate}-\text{Exercise rate, 0})]$$

On the other hand, a put option on interest rates has a positive payoff when the current spot rate is less than the exercise rate.

$$\text{Put payoff}=\text{Notional Amount}\times[\text{Max}(\text{Exercise rate}-\text{Current spot rate},0)]$$

We can apply the binomial model to value such interest rate options.

Example: Calculating the value of an interest rate European option

Consider a two-year European-style call option with a one-year spot rate compounded annually as the underlying. The exercise rate is 6%. The two-period interest rate tree is given below:

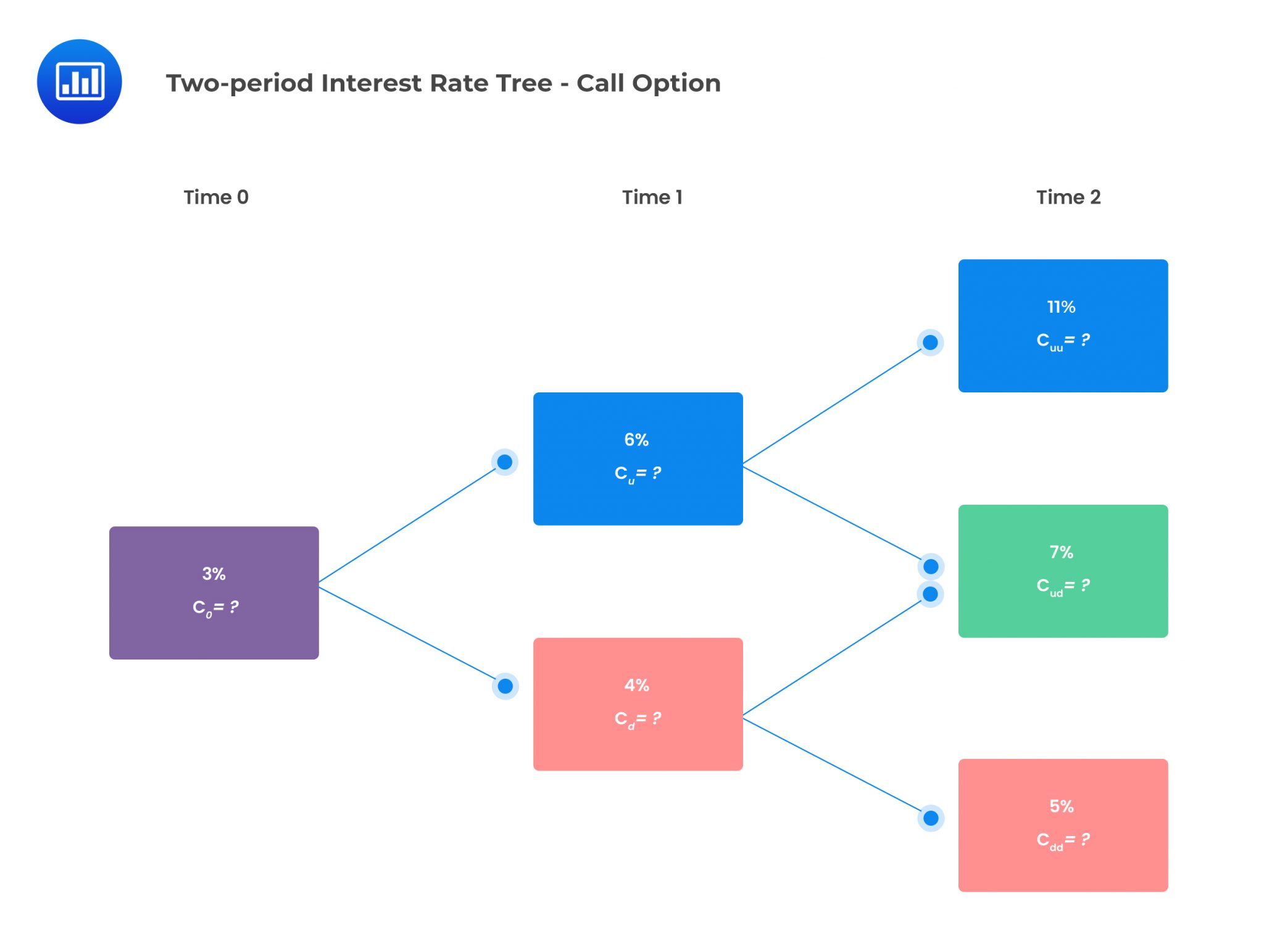Suppose that the notional principal of each option is $500,000, and the risk-neutral probability of an up jump is 0.5. The value of the European call option can be determined as follows:

Payoffs at time 2

$$\begin{align*}\text{c}_{\text{uu}}&=\text{Max}(0,\text{S}_{0}\text{u}^{2}-\text{K})\\&=\text{Max}(0,0.11-0.06)\\&=0.05\end{align*}$$

$$\begin{align*}\text{c}_{\text{ud}}&=\text{Max}(0,\text{S}_{0}\text{ud}-\text{K})\\&=\text{Max}(0,0.07-0.06)\\&=0.01\end{align*}$$

$$\begin{align*}\text{c}_{\text{dd}}&=\text{Max}(0,\text{S}_{0}\text{d}^{2}-\text{K})\\&=\text{Max}(0,0.05-0.06)\\&=0\end{align*}$$

Value of call at time 1

$$\begin{align*}c_{u}&=PV_{1,2}[qc_{uu}+(1+q)c_{ud}]\\&=\frac{1}{1.06}[0.5\times0.05+(1-0.5)\times0.01]\\&=0.028302\end{align*}$$

$$\begin{align*}c_{d}&=PV_{1,2}[qc_{ud}+(1-q)c_{dd}]\\&=\frac{1}{1.04}[0.5\times0.01+(1-0.5)\times0]\\&=0.004808\end{align*}$$

Value of call at time 0

$$\begin{align*}c_{0}&=PV_{0,1}[qc_{u}+(1-q)c_{d}]\\&=\frac{1}{1.03}[0.5\times0.028302+(1-0.5)\times0.004808]\\&=0.01607\end{align*}$$

The call value at time 0 is then obtained by multiplying with the notional amount:

$$\text{Call value}=0.01607\times$500,000=$8,035$$

Question

Consider a two-year European-style put option with the annually compounded one-year spot interest rate as the underlying. The exercise rate is 6%. The two-period interest rate tree is given below:

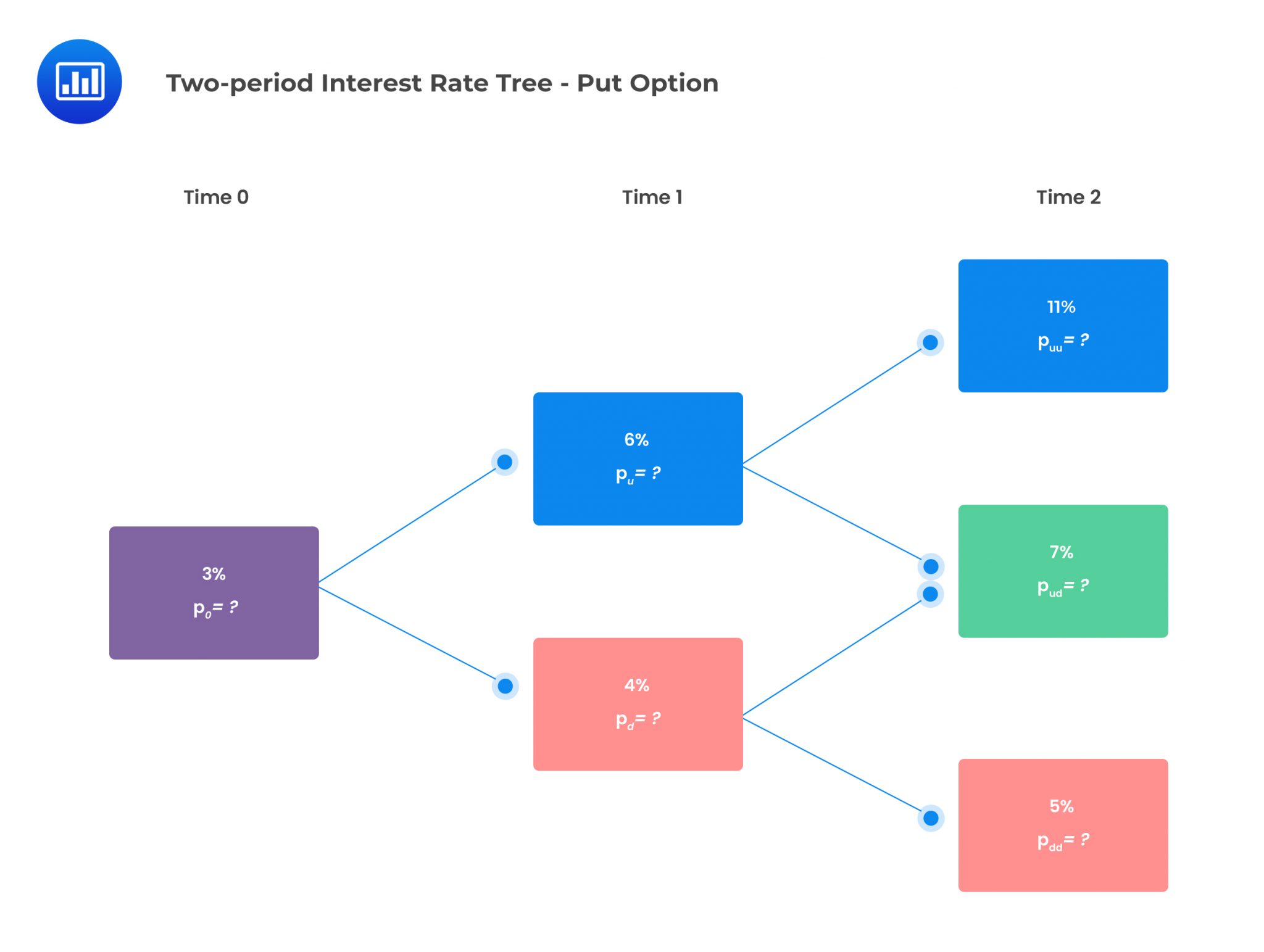Suppose that the notional principal of each option is $500,000, and the risk-neutral (RN) probability of an up jump is 0.5. The value of the European put option is closest to: 

1. $1,167
2. $5,835
3. $8,035

Solution

The correct answer is A: 

Put Payoffs at time 2

Similar to a call option, a put option will have three possible payoffs:

$$\begin{align*}p_{uu}&=Max(0,K-S_{0}u^{2})\\&=Max(0,0.06-0.11)\\&=0\end{align*}$$

$$\begin{align*}p_{ud}&=Max(0,K-S_{0}ud)\\&=Max(0,0.06-0.07)\\&=0\end{align*}$$

$$\begin{align*}p_{dd}&=Max(0,K-S_{0}dd)\\&=max(0,0.06-0.05)\\&=0.01\end{align*}$$

Value of put at time 1

$$\begin{align*}p_{u}&=PV_{1,2}[qp_{uu}+(1-q)p_{ud}]\\&=\frac{1}{1.06}[0.5\times0+(1-0.5)\times0]\\&=0\end{align*}$$

$$\begin{align*}p_{d}&=PV_{1,2}[qp_{ud}+(1-q)c_{dd}]\\&=\frac{1}{1.04}[0.5\times0+(1-0.5)\times0.01]\\&=0.004808\end{align*}$$

Value of put at time 0

$$\begin{align*}p_{0}&=PV_{0,1}[qp_{u}+(1-q)p_{d}]\\&=\frac{1}{1.03}[0.5\times0+(1-0.5)\times0.004808]\\&=0.00233398\end{align*}$$

The put value at time 0 is then obtained by multiplying by the notional amount:

$$\text{put value}=0.002334\times$500,000=$1,167$$

Reading 38: Valuation of Contingent Claims

LOS 38 (d) calculate and interpret the value of an interest rate option using a two-period binomial model;