Binomial Option Valuation Model

Contingent Claims

A contingent claim is a derivative contract that gives the owner the right but not the obligation to receive a future payoff that depends on the value of the underlying asset. Call and put options are examples of contingent claims.

So far, the approaches we have used to price and value derivative contracts rest on the no-arbitrage principle. This principle states that prices adjust so as not to follow arbitrage profits.

The arbitrageur must follow the following two rules:

Rule 1: Do not use your own money.

Rule 2: Do not take any price risk.

The no-arbitrage valuation methodology applied in this reading is based on the law of one price. This law argues that two investments with comparable future cash flows have the same current price regardless of what happens in the future.

Binomial Option Valuation Model

One-period Binomial Option Valuation Model

In the one-period binomial model, we start today (at time \(t = 0\)) when the stock price is \(S_0\). The stock price can then either jump upwards or downwards over the one-period time interval, to \(t=1\). This is illustrated below:

$$ S_1= {\left\{\begin{matrix} S_0u, & \text{if the stock price jumps up} \\ S_0d, & \text{if the stock price jumps down} \end{matrix}\right. } $$

This can be shown in the following binomial tree:

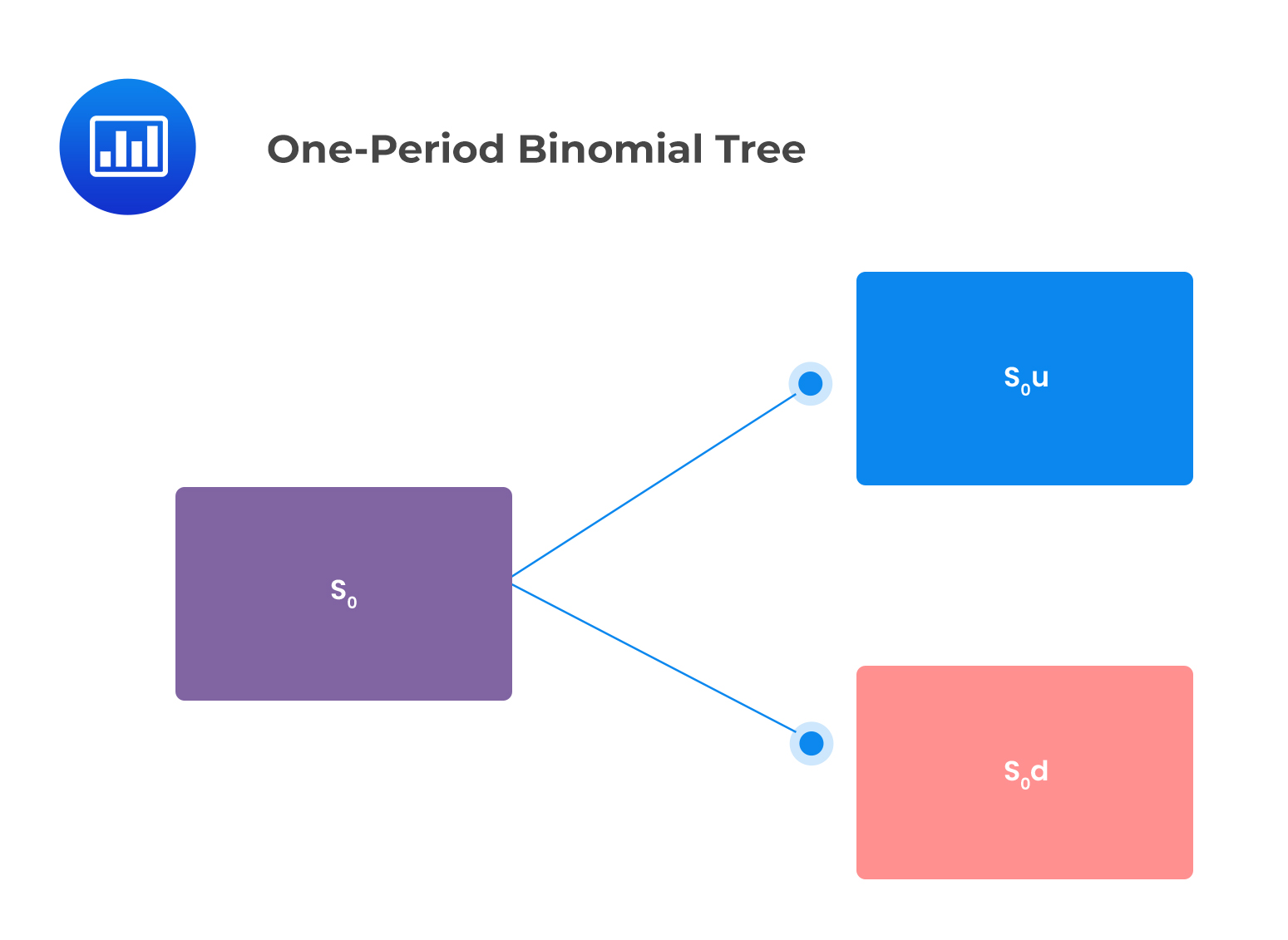Where:

$$ \begin{align*} u& =\frac{S_0u}{S_0} \\ d & =\frac{S_0d}{S_0} \end{align*} $$

One-period Binomial Option Payoffs

Consider a call option that pays \(c_u\) if the price of the underlying asset jumps up and \(c_d\) if the price of the underlying asset jumps down.

The value of the call option at expiry is expressed as:

\(c_u = Max\left(0,S_0u-K\right),\) if the price of the underlying jumps up

and

\(c_d = Max{\left(0,S_0d-K\right)},\) if the stock price jumps down

Where \(K\) is the strike price.

This is shown in the following binomial tree:

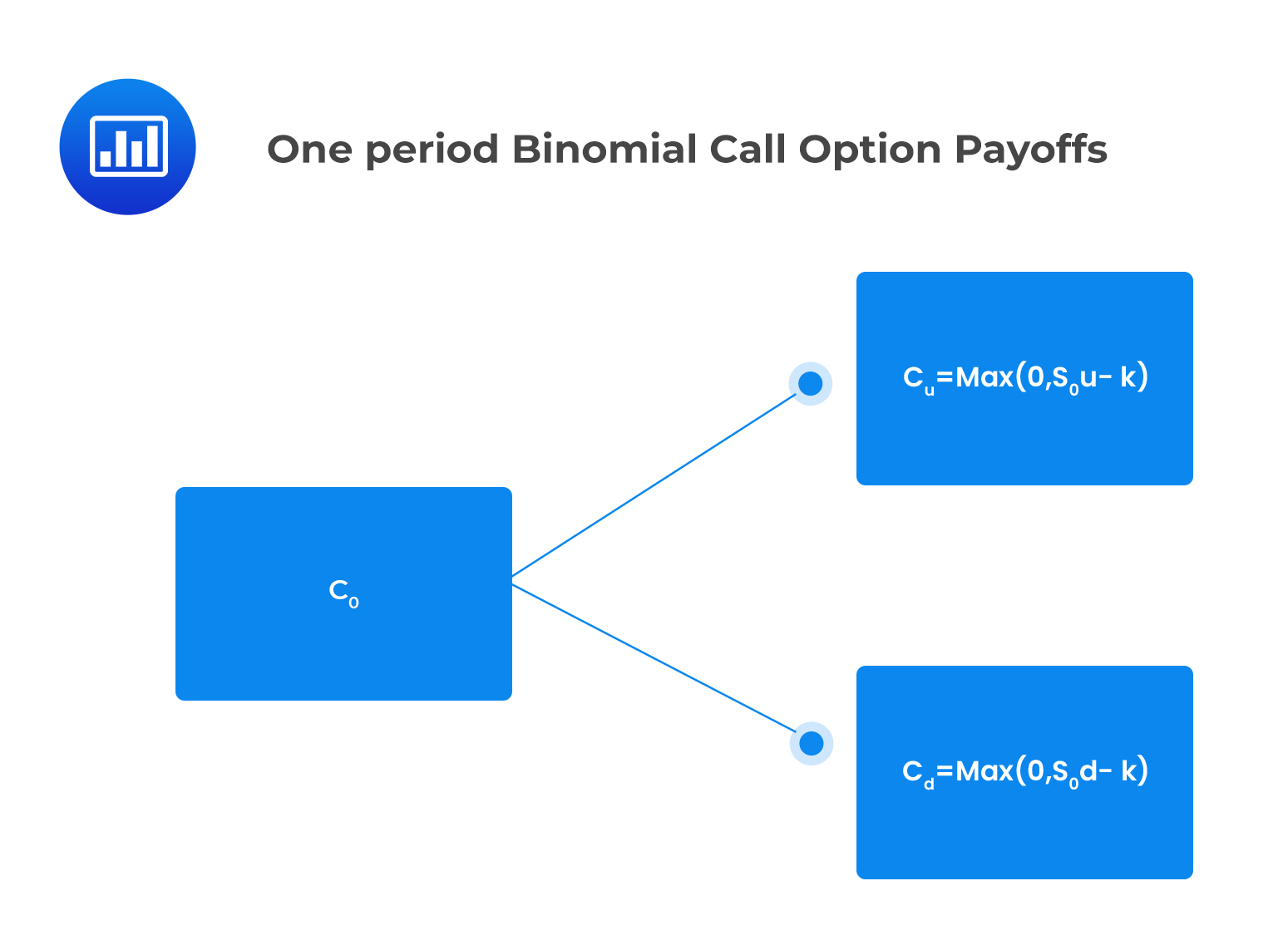Similarly, the value of a put option at expiration is given by:

\( p_u=Max\left(0, K-S_0u\right),\) if the price of the underlying asset jumps up $$

and

\(p_d=Max \left(0, K-S_Od \right)\) if the price of the underlying asset jumps down.

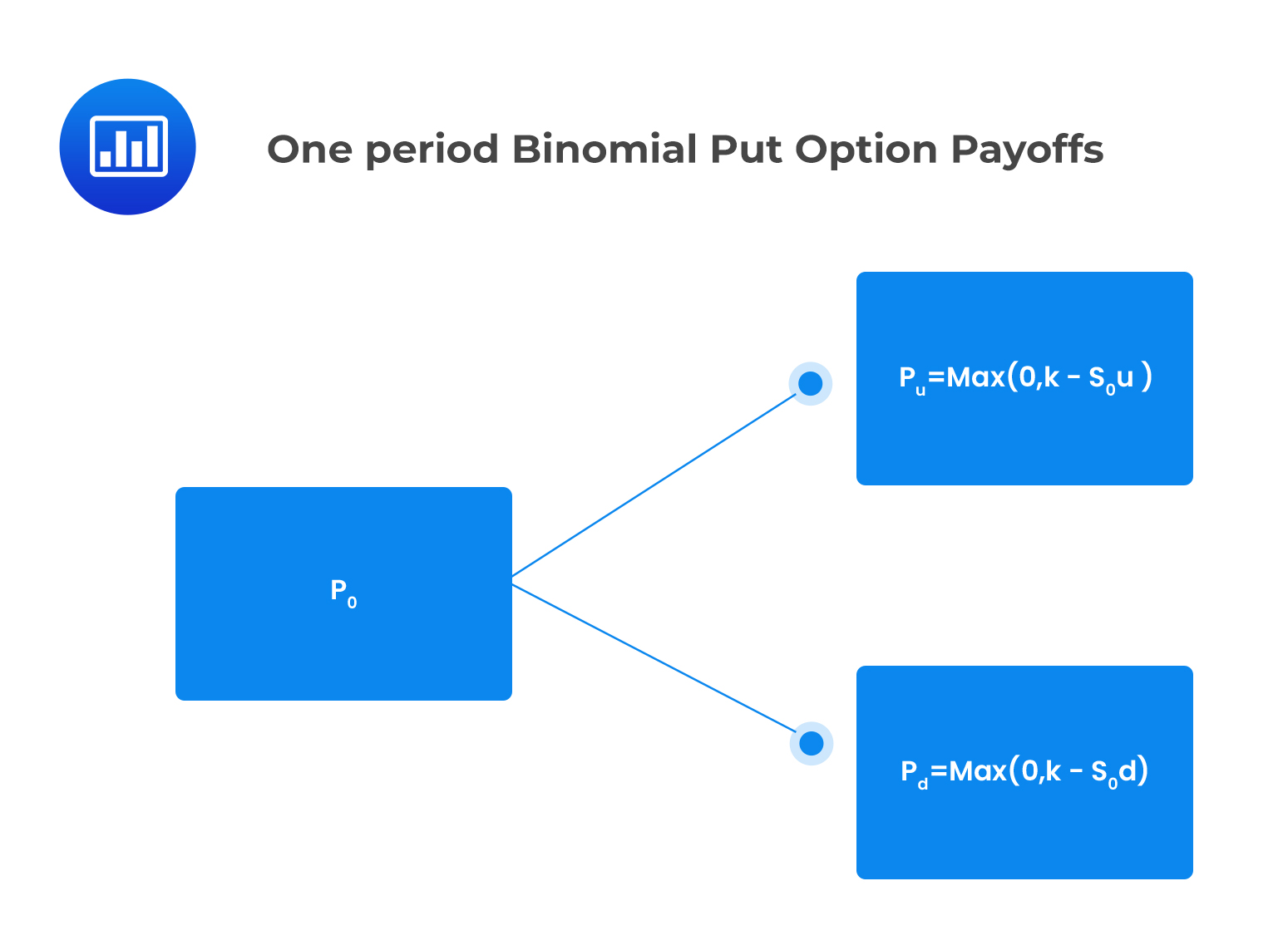One-period Binomial Option Values

The initial values of call and put options with a one period to expiry are determined using the following formulas:

$$ c_0=\frac{qc_u+\left(1-q\right)c_d}{1+r} $$

and

$$ p_0=\frac{qp_u+\left(1-q\right)p_d}{1+r} $$

Where:

$$ q=\frac{\left(1+r\right)-d}{u-d} $$

Where:

\(r\) is the risk-free rate for a single period.

\(q\) gives the risk-neutral probability of an upward move in price

\(1-q\) gives the risk-neutral probability of a downward move

Example: Calculating the Price of an Option Using the One-period Binomial Option Valuation Model

Consider a European put option with a strike price of $50 on a stock whose initial price is $50. The risk-free rate of interest is 4%, the up-move factor u = 1.20, and the down move factor d = 0.83. The price of the put option can be determined using the one-period binomial model as follows:

$$ \begin{align*} S_0u& =50\times1.20=$60 \\ S_0d &= 50\times0.83=$41.50 \end{align*} $$

Recall that put payoff is given by:

\( p_u=Max\left(0, K-S_0u\right),\) if the price of the underlying asset jumps up

and

\(p_d=Max (0, K-S_Od)\) if the price of the underlying asset jumps down.

$$ \begin{align*} p_u &=Max\left(0,50-60\right)=$0 \\ p_d & =Max\left(0,60-41.50\right)=$18.50 \end{align*} $$

The value of the put is then calculated using the formula:

$$ p_0=\frac{qp_u+\left(1-q\right)p_d}{1+r} $$

Where:

$$ \begin{align*} q &=\frac{\left(1.04\right)-0.83}{1.20-0.83}=0.5676 \\ p_0 &=\frac{0.5676\times$0+0.4324\times$18.50}{1.04}=$7.69 \end{align*} $$

Two-Period Binomial Option Valuation Model

The one-period binomial model can be extended into a multi-period context. The two-period binomial lattice can be seen as three-one period binomial lattices as shown below:

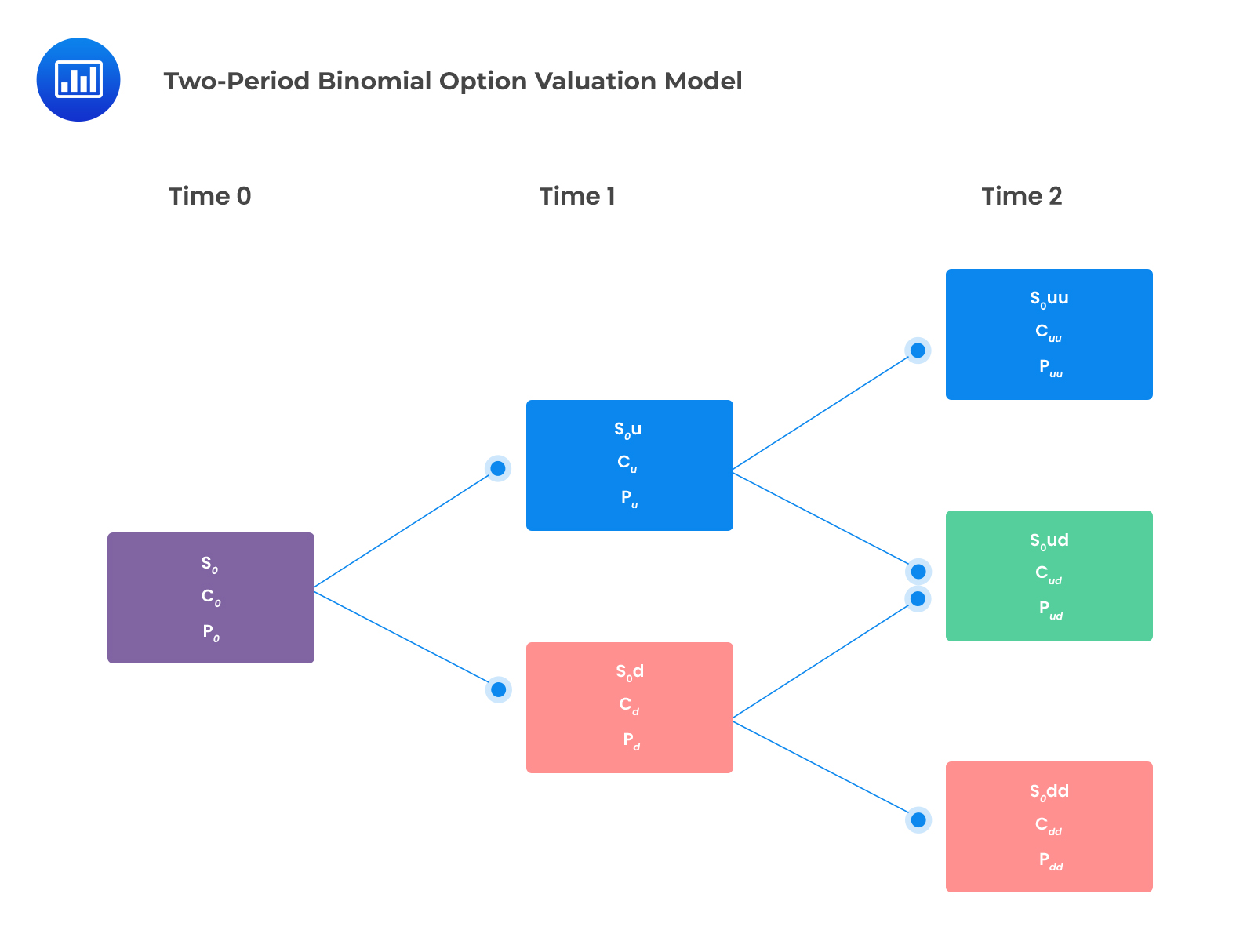The underlying asset can result in only three possible values:

• \(S_0uu\) = When price moves up twice.
• \(S_0ud\) = When price either moves up then down or down then up.
• \(S_0dd\) = When price moves down twice.

Call Payoffs

A call option under the two-period binomial option model will have three possible payoffs at expiry as follows:

$$ \begin{align*} c_{uu} &=max \left(0, S_0u^2-K\right) \\ C_{ud} &=Max\left(0,S_0ud-K\right) \\ c_{dd} & =Max(0,S_0d^2-K) \end{align*} $$

Put Payoffs

Similar to a call option, a put option will have three possible payoffs:

$$ \begin{align*} p_{uu}& = Max(0,K – S_0u^2) \\ p_{ud}& = Max(0,K – S_0ud) \\ p_{dd} & = Max(0,K – S_0d^2) \end{align*} $$

Option Values

A European call option’s value can be determined using the two-step binomial valuation model using the following formula.

$$ c_o=\frac{q^2c_{uu} + 2q\left(1-q\right)c_{ud}\ +\left(1 – q\right)^2c_{dd}}{\left(1 + r\right)^2} $$

The two-period European put value is given as:

$$ p_o=\frac{q^2p_{uu} + 2q\left(1-q\right)p_{ud} +\left(1 – q\right)^2p_{dd}}{\left(1 + r\right)^2} $$

These concepts will be explained more with examples in the sections that follow.

Question

A one-year European call option has a strike price of £60. The underlying non-dividend-paying stock is currently trading at £60. Over one year, the stock price can either jump up to £90 or jump down to £50. The annual risk-free interest rate is 4%. Using a one-period binomial option valuation model, the price of the call option is closest to:

1. £2.44.
2. £9.04.
3. £15.64.

Solution

The correct answer is B.

The payoff of a European call option at expiration is given by:

\(c_u=Max\left(0, S_0u-K\right),\) if the price of the underlying jumps up

and

\(c_d=Max{\left(0,S_0d-K\right)},\) if the stock price jumps down

$$ \begin{align*} u &=\frac{90}{60}=1.5 \\ d &=\frac{50}{60}=0.83 \\ c_u &=Max\left(0,90-60\right)=£30 \\ c_d &=Max\left(0,50-60\right)=£0 \end{align*} $$

The value of a call option is then calculated using the formula:

$$ c_0 =\frac{qc_u+\left(1-q\right)c_d}{1+r} $$

Where:

$$ \begin{align*} q &=\frac{1.04-0.83}{1.5-0.83}=0.3134 \\ c_0 &=\frac {0.3134× £30+0.6866×£0}{1.04}=£9.04 \end{align*} $$

Reading 34: Valuation of Contingent Claims

LOS 34 (a) Describe and interpret the binomial option valuation model and its component terms.