Multiple Regression Model
Consider the multiple regression of the price of the US Dollar index on... Read More
The idea that a hedged portfolio returns the risk-free rate can determine the initial value of a call or put. The expectations approach calculates the values of the option by taking the present value of the expected terminal option payoffs. This approach utilizes risk-neutral probabilities instead of true probabilities.
Thus, the initial value of a call and put respectively are determined using the following formulas:
$$c_{0}=\frac{qc_{u}+(1-q)c_{d}}{1+r}$$
And
$$p_{0}=\frac{qp_{u}+(1-q)p_{d}}{1+r}$$
Where:
$$q=\frac{(1+r)-d}{u-d}$$
\(r\) is the risk-free rate for a single period.
\(q\) gives the risk-neutral probability of an upward move in price, and \((1-q)\) gives the probability of a downward move.
Consider a stock that is currently trading at $50. Assume that the up jump and down jump factors for the stock price are u = 1.20 and d = 0.80. The risk-free rate compounded periodically is 4%. Given a strike price of $50, we can use a single period binomial model to price European call and put options.
Recall:
$$c_{T}=max(S_{T}-K,0)$$
$$S_{0}u=50\times1.20=$60$$
$$S_{0}d=50\times0.80=$40$$
$$c_{u}=max($60-$50,0)=$10$$
$$c_{d}=max($40-$50,0)=$0$$
The value of the call option can then be determined using the formula:
$$c_{0}=\frac{qc_{u}+(1-q)c_{d}}{1+r}$$
Where:
$$\begin{align*}q&=\frac{(1+r)-d}{u-d}\\&=\frac{(1.04)-0.8}{1.20-0.80}\\&=0.6\end{align*}$$
$$c_{0}=\frac{0.6\times$10+(1-0.6)\times0}{1.04}=$5.77$$
$$p_{T}=max(K-S_{T},0)$$
$$p_{u}=max($50-$60,0)=$0$$
$$p_{d}=max($50-$40,0)=$10$$
$$\begin{align*}p_{0}&=\frac{qp_{u}+(1-q)p_{d}}{1+r}\\&=\frac{0.60\times0+(1-0.60)\times$10}{1.04}\\&=$3.85\end{align*}$$
The expectations approach can also be applied to the two-step binomial model to determine the value of options.
Let q to be the risk-neutral probability of an up move, the price of a European call option can be determined using the two-step binomial model:
$$c_{o}=\frac{q^{2}c_{uu}+2q(1-q)c_{ud}+(1-q)^{2}c_{dd}}{(1+r)^2}$$
The two-period European put value is given as:
$$p_{0}=\frac{q^{2}p_{uu}+2q(1-q)p_{ud}+(1-q)^{2}p_{dd}}{(1+r)^{2}}$$
Suppose you have a stock that is currently trading at $60. A two-year European call option on the stock is available with a strike price of $60. The risk-free rate of 2% per annum. Given that the up-move factor is 1.10 and the down-move factor is 0.90, the value of the call option using a two-period binomial model is closest to:
The risk-neutral probability of an up-move is given by:
$$\begin{align*}q&=\frac{(1+r)-d}{u-d}\\&=\frac{1.02-0.90}{1.1-0.9}\\&=0.6\end{align*}$$
The probability of down move \((1-q) = 1-0.6 = 0.4\)
The two-period binomial tree is shown below:
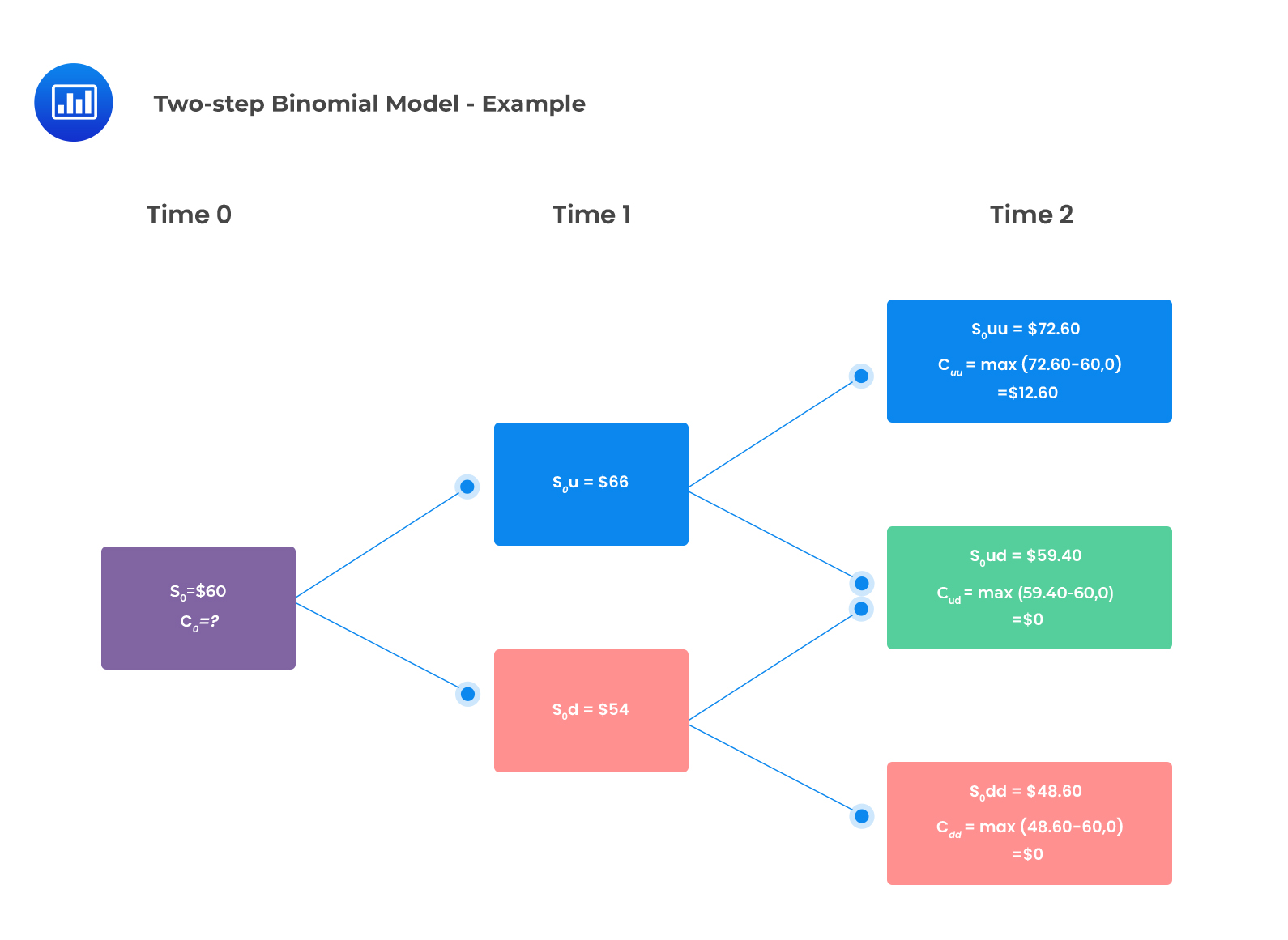 The two-period binomial value of the call option:
The two-period binomial value of the call option:
$$\begin{align*}c_{o}&=\frac{q^{2}c_{uu}+2q(1-q)c_{ud}+(1-q)^{2}c_{dd}}{(1+r)^{2}}\\&=\frac{0.6^{2}\times$12.60+2\times0.6\times0.4\times0\times0.4^{2}\times0}{(1.02)^{2}}\\&=$4.36\end{align*}$$
Question
Nabi Gudka, CFA, applies the expectations approach to value a European call option on the common shares of Wipro Inc.
The expectation approach most likely utilizes:
- A risk premium for discounting
- Risk-neutral probabilities
- Actual probabilities
Solution
The correct answer is A:
Under the expectations approach, the expected future payoff is calculated using risk-neutral probabilities, and the expected payoff is discounted at the risk-free rate.
Reading 38: Valuation of Contingent Claims
LOS 38 (e): Describe how the value of a European option can be analyzed as the present value of the option’s expected payoff at expiration;