Liquidity Risk Reporting and Stress Te ...
After completing this reading, you should be able to: Identify best practices for... Read More
After completing this reading, you should be able to:
Factor risks threaten the expected returns of assets, resulting in the potential downside. The risk premium is the reward for these potential downsides as compared to holding a risk-free asset. Different factors present a different set of challenges. For instance, high inflation and low economic growth define bad economic times. Risk premiums compensate investors exposed to these losses by magnifying the returns during good economic times.
Asset prices can be affected by various factors, including volatility, inflation, interest rates, and economic growth, among others.
Factors behind the assets are key, not the assets: The exposure to the underlying risk factors is what matters rather than the exposure to the specific assets.
Assets are bundles of factors: Some asset classes such as equities and government fixed-income securities can be seen as factors, while others such as hedge funds and corporate bonds may contain many different factors such as interest rate risk, default risk, volatility risk, among others.
Different investors have varying optimal exposures to risk factors: For example, during times of high volatility, such as the 2008-2009 financial crisis, many assets and strategies lose money. These times are not favorable to most investors and, therefore, investors seek protection against large increments in volatility. However, a few brave (and often younger) investors can wither losses during these times and stand a chance to benefit from a volatility premium during normal times. They are paid risk premiums as compensation for taking losses during volatile times.
The CAPM was the first logical theory to peg the risk of an asset on its (asset’s) movement relative to the other assets and the market as a whole as opposed to how that asset behaves in isolation.
CAPM assumes that asset risk premiums depend only on an asset’s beta and that market portfolio is the only factor that matters. However, numerous empirical studies have demolished CAPM assumptions. Empirical evidence shows that CAPM beta does not fully explain the cross-section of the expected asset returns. This is an implication that additional factors are required to characterize the behavior of asset returns appropriately. This, therefore, naturally leads to the creation of multifactor pricing models.
Under the CAPM, the factors underlying the assets influence asset risk premiums. These risk premiums are the rewards for losses incurred by investors during bad times. Risk is a property of how assets move relative to each other.
CAPM’s main assumptions include the following:
The following are the crucial lessons that the CAPM holds:
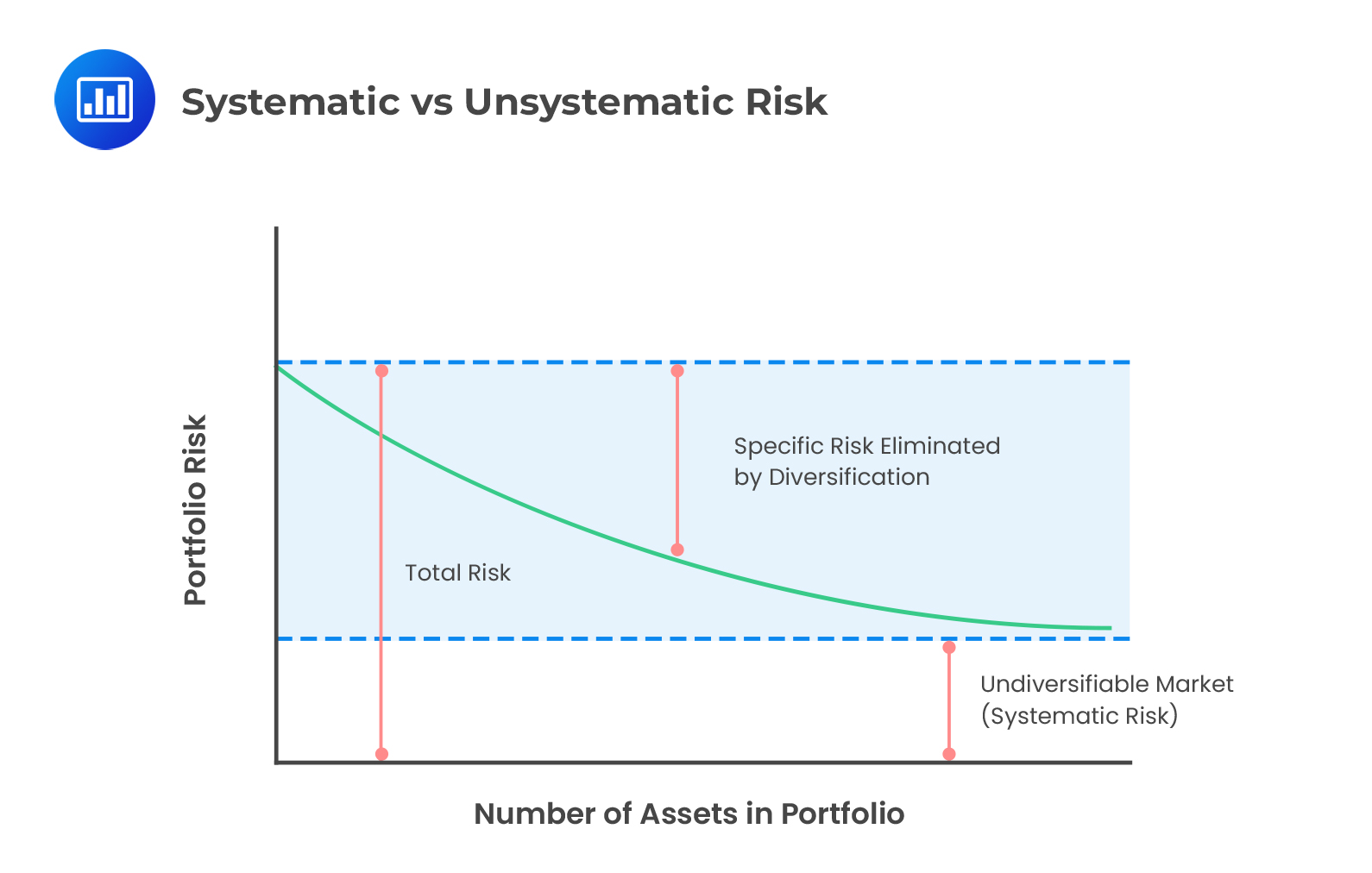
Under the CAPM, the market portfolio is the only existing factor, and each stock is held proportionally to its market capitalization. Individual stocks are exposed to the market factor, which is rewarded by the risk premium. However, stocks are also exposed to idiosyncratic risk, which is not rewarded. By holding the market factor portfolio, the idiosyncratic part can be diversified away by investors, thereby increasing their returns.
All investors will hold market portfolios, albeit, in varying proportions. Remember that each investor possesses a varied amount of factor exposure. In other words, investors hold different combinations of risk-free assets and risky portfolios, representing various positions along the capital allocation line.
According to CAPM, an asset’s risk is measured in relation to its factor exposure. A factor having a positive risk premium implies a higher exposure to that factor and a higher expected return on the asset. These high beta assets behave just like the diversified portfolio held by an investor. For this reason, high expected returns are required for investors to hold them. On the contrary, there are assets that pay off when the market tanks are valuable and have low betas. These low beta assets have diversification benefits, making them very attractive to hold.
The risk premium of a particular asset is derived under the CAPM formula using beta pricing to construct the security market line (SML). The formula states that:
$$ \begin{align*} \text{E}\left( { \text{R} }_{ \text{i} } \right) & =\text{R}_{ \text{F} } +\cfrac { \text{cov}\left( { \text{R} }_{ \text{i} },{ \text{R} }_{ \text{M} } \right) }{ \text{Var}\left( { \text{R} }_{ \text{M} } \right) } \times \left[ \text{E}\left( { \text{R} }_{ \text{M} } \right) -{ \text{R} }_{ \text{F} } \right] \\ \\ & = \text{R}_{ \text{F} } + { \beta }_{ \text{i} }\times \left[ \text{E}\left( { \text{R} }_{ \text{M} } \right) -{ \text{R} }_{ \text{F} } \right] \end{align*} $$
Where:
According to the CAPM’s beta pricing relationship, also called the security market line (SML), a risk premium in CAPM is a reward for how an asset pays off in bad times. These bad times are with respect to the factor and the market portfolio. As such, bad times correspond to low market returns. There are assets that experience losses when the market losses during bad times are said to have a high beta. It is noteworthy that, on the other hand, if an asset pays off when the market is experiencing losses, it is said to have a low beta. If the payoff of an asset is high in bad times, then the asset is valuable to hold, and its risk premium is low. Moreover, if its payoff is low in bad times, then the asset is risky, and its risk premium must be high.
The market portfolio is representative of the average holdings across investors. The tangency point between the capital allocation line (CAL) and the mean-variance frontier represents the average investor, or an investor holding 100% of the mean-variance efficient (MVE) portfolio. The risk aversion corresponding to the 100% portfolio position is the market’s risk aversion.
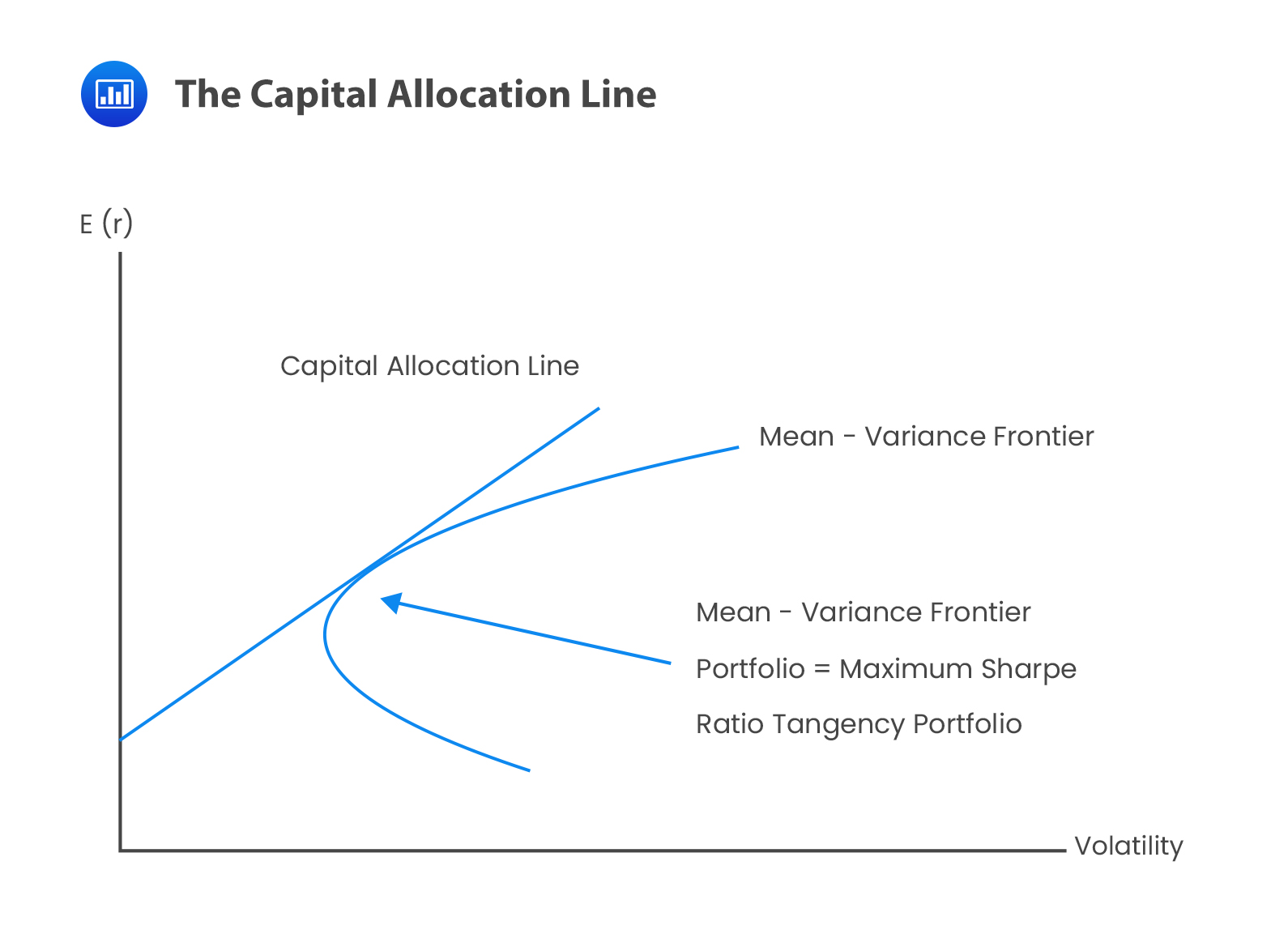 Investors will get exposed to more or less market factor risks depending on their risk preferences. This is because each investor differs from the average investor.
Investors will get exposed to more or less market factor risks depending on their risk preferences. This is because each investor differs from the average investor.
The capital allocation line (CAL) for a single investor is referred to as the capital market line (CML) in equilibrium. This is because, under the CAPM assumptions, every investor has the same CML. The equation for the CML pins down the market risk premium:
$$ \text{E}\left( { \text{r} }_{ \text{m} } \right) -{ \text{r} }_{ \text{f} }= {\overline{ \gamma} { \sigma }_{ \text{m} }^{ 2 } } $$
Where:
\({\text{E}}\left({\text{r}}_{\text{m}} \right)-{\text{r}}_{\text{f}}\) is the market risk premium.
\(\overline { \gamma } \) is the risk aversion of the “average” investor.
\({\sigma}_{\text{m}}^{2}\) is the volatility of the market portfolio.
From the above equation, as the volatility of the market portfolio increases, the market’s expected return increases, and equity prices fall simultaneously. We observe that the market risk premium is proportional to market variance since investors prefer expected returns to variances under CAPM. The market removes all idiosyncratic risks, and the remaining risks are rewarded. The above equation gives the risk premium of the market.
The following are the implications of using CAPM for asset valuation:
Equilibrium occurs when investors’ demand for assets is equal to the supply of the assets. According to CAPM, the market is the factor in equilibrium since everyone holds the mean-variance efficient (MVE) portfolio (except for the infinitely risk-averse individuals). If everyone’s optimal risky portfolio assigns zero weight to a particular asset, Stock A for instance, then, equilibrium is untenable. Therefore, Stock A must be held so that supply equals demand. Alternatively, Stock A can be overpriced so that its expected return is too low, leading to the price falling.
Under the CAPM assumptions, the expected payoff of Stock A stays constant, and therefore, as its price falls, its expected return increases. The price falls until investors are willing to hold the exact number of Stock A shares outstanding. Therefore, the expected return is in equilibrium.
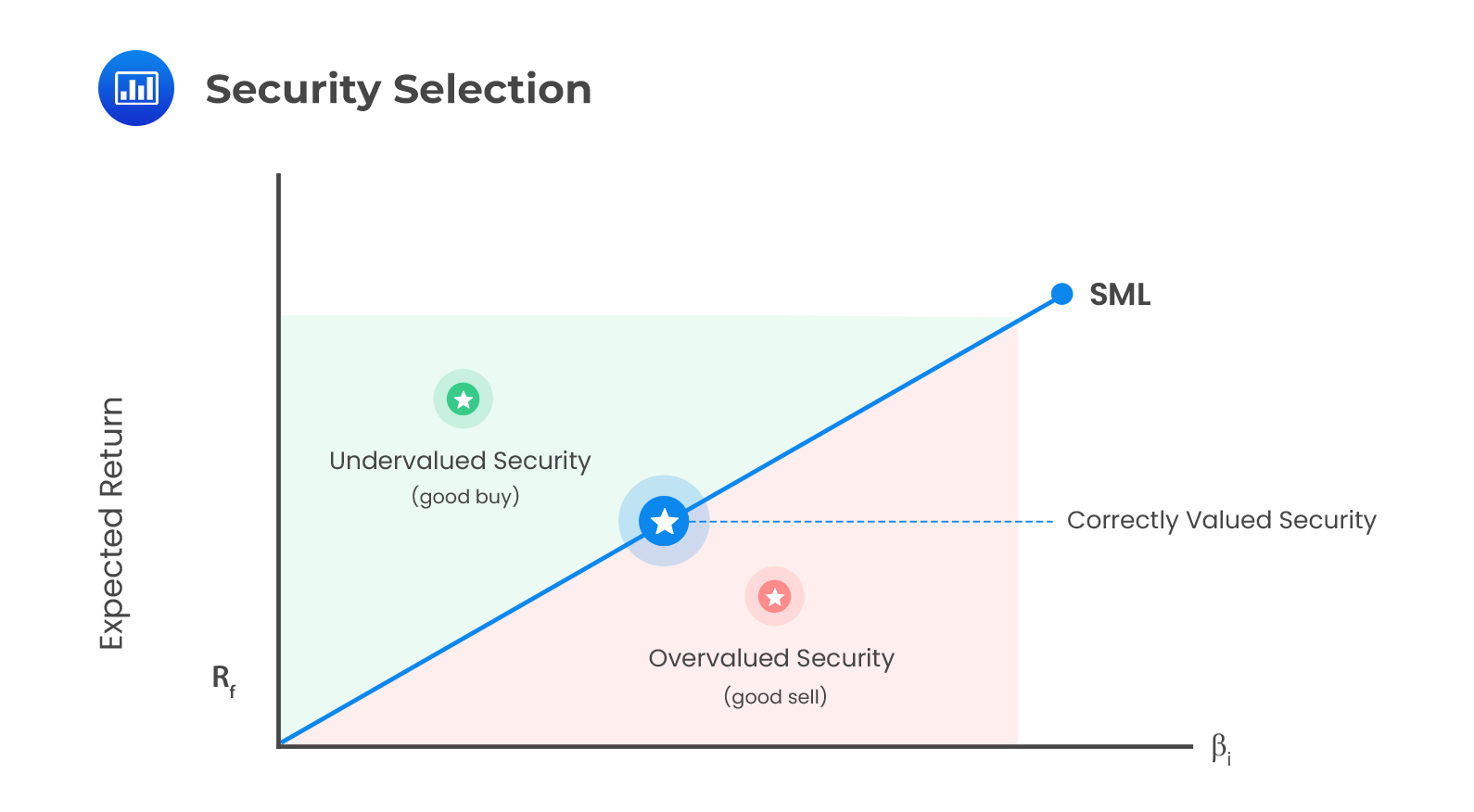 ii. Exposure to Factor Risk
ii. Exposure to Factor RiskCAPM identifies the required rate of return to be used to find the present value of an asset with any specific level of systematic risk. In equilibrium, the asset’s expected return should be plotted at the same point as the systematic risk coefficient. If the asset’s expected rate of return is not equal to its required rate of return, then the asset is labeled either as underpriced or overpriced.
A diversification benefit exists when an asset’s standard deviation can be reduced without reducing its expected return. According to the CAPM, the market portfolio is the only existing factor, with each stock being held proportionally to its market portfolio. This corresponds to a market index fund. For optimal development of the factor, many assets have to be held to diversify away from the idiosyncratic (or nonfactor) risk.
With the absence of perfect correlation, diversification ensures that when one asset performs poorly, some other assets perform well. This way, gains partly offset losses. Instead of investors holding assets in isolation, they somewhat improve their risk-return trade-off through diversifying and holding portfolios of assets. This balance across many non-perfectly correlated assets improves the reward-to-risk ratio (Sharpe ratio). Investors will continue diversifying until they hold the most diversified portfolio possible, that is, the market portfolio. The market factor is the best and most-well diversified portfolio that investors can hold under the CAPM.
 Shortcomings of CAPM
Shortcomings of CAPMCAPM works because of several assumptions made. However, most of these assumptions are unrealistic since they do not reflect the real world. We look at some of these assumptions and the shortcomings associated with them:
The income streams and liabilities of investors are unique. As such, their optimal portfolio choice must take this into account. The denomination of liabilities should be in real terms since the living standard should be maintained even when prices are shooting up. Income streams are typically risky, and income declines during low economic growth periods. Therefore, variables such as inflation and economic growth are important factors since many investors’ income and liabilities change as these macro variables change.
It is often the case that more realistic utility functions have an asymmetric risk treatment. This is because investors are generally more distressed by losses than they are pleased by gains. Deviations should then be expected from the CAPM among stocks with different downside risk measures. Researchers have shown that stocks with more significant downside risk have higher returns and that other higher moment risks, such as skewness and kurtosis, also carry risk premiums.
A one-period investment horizon is by itself a minor assumption. There is a huge implication when the choice of a portfolio is extended to a dynamic, long-horizon setting, despite the long investment horizon being an inconsequential assumption for the CAPM theory. Rebalancing is the optimal strategy for long-term investors, but an average investor holding the market portfolio does not rebalance.
With this assumption, the same portfolio is held by all investors in the CAPM world. Moreover, this portfolio becomes the market portfolio, in equilibrium. However, in reality, people rarely share similar beliefs since their expectations are heterogeneous.
Expected returns are affected by taxes. Therefore, taxes should be regarded as a systematic factor. Besides, there are variations in transaction costs across all securities. There may be more deviations from CAPM for the very illiquid market with high transaction costs.
Informed investors move prices since they may have some knowledge that others may lack.
There are costs incurred in the collection and processing of information, and particular information may not be availed to all investors.
With multifactor models, it is recognized that the definition of bad times can be broader in comparison to just bad returns on the market portfolio. They employ multiple factors in explaining bad times. Additionally, when building a multifactor model, there is no clarity on neither the factors nor the required number of factors.
CAPM uses the market factor as the only factor that defines bad times. However, the market factor can be split up even further into different macroeconomic factors. These may include inflation, interest rates, and business cycle uncertainty, among others.
The lessons from multifactor models are similar to the lessons from the CAPM:
A stochastic discount factor (SDF) is an approach for asset pricing that uses the notion of a pricing kernel to capture the composite bad times over multiple factors.
The SDF is denoted as \(m\) in the multifactor model. The single variable \(m\) is used to capture all the bad times, providing an extremely powerful notation to capture bad times with multiple variables. CAPM is a special case of this model, where \(m\) is linear in the market return. That is,
$$ \text{m}=\text{a}+{\text{br}}_{\text{m}} $$
Where \(a\) and \(b\) are constants.
With this \(m\) notation, multiple factors can be specified by having the SDP depend on a \(k\) “bad times” variable as shown below:
$$ \text{m}=\text{a}+{\text{b}}_{1}{\text{f}}_{1}+{\text{b}}_{2}{\text{f}}_{2}+…+{\text{b}}_{k}{\text{f}}_{k} $$
where \({\text{f}}_{\text{i}}\)’s are the factors defining different bad times.
Regardless of the approach used in asset pricing, each model typically comes down to the same financial concept that “the price of an asset equals its expected discounted payoff.” The following equation by Euler formally expresses this:
$$ {\text{P}}_{\text{i}}=\text{E}\left[{\text{md}}_{\text{i}}\right] $$
Where:
The name “stochastic discount factor” arises because the payoffs are discounted using \(m\). The SDF is called a pricing kernel. The word “kernel” is borrowed from statistics, since it can be estimated using a kernel estimator. It is called a “pricing kernel” because it prices all assets.
All risk corrections are incorporated by defining one single SDF. Therefore, an empirically rigorous SDF should be modeled. However, the modeling of such SDFs is difficult, presenting challenges in asset pricing.
By dividing both sides of the Euler equation by the price \(\text P_{\text i}\), we obtain an expression in terms of returns:
$$ 1=\text{E}\left[\text{m}\left(1+{\text{r}}_{\text{i}}\right)\right], $$
where \(1+{\text{r}}_{\text{i}}= \cfrac{{\text{d}}_{\text{i}}}{{\text{p}}_{\text{i}}}\) , is the gross return on asset i.
The above equation gives a risk-free asset. The price of a risk-free bond is therefore given by:
$$ \cfrac{1}{1+{\text{r}}_{\text{f}}}=\text{E}\left[\text{m}\right] $$
Multiple factors in an SDF result in the following multi-beta relation for an asset’s risk premium:
$$ \text{E}\left( { \text{r} }_{ \text{i} } \right) ={ \text{r} }_{ \text{f} }+{ \text{b} }_{ \text{i},1 }\text{E}\left( { \text{f} }_{ 1 } \right) +{ \text{b} }_{ i,2 }\text{E}\left( { \text{f} }_{ 2 } \right) +…+{ \text{b} }_{ \text{i},\text{k} }\text{E}\left( { \text{f} }_{ \text{k} } \right) $$
Where :
\({ \text{b} }_{ \text{i},\text{k} }\) is the beta of asset i for factor k.
\(\text{E}\left( { \text{f} }_{ \text{k} } \right)\) is the risk premium of factor k.
According to the efficient market hypothesis (EMH), also known as the efficient market theory, share prices reflect all available information, and it is not possible to generate consistent excess returns.
Economists no longer believe that markets are perfectly efficient. As a matter of fact, markets cannot be perfectly efficient in their pure form.
Grossman and Stiglitz developed the notion of market near-efficiency in order to describe a world in which markets are near-efficient. In doing so, they resolved a conundrum arising from the CAPM’s assumption that information is costless.
Assume that collecting and trading information is expensive, as it is in the real world. In that case, why would anyone invest in gathering information if all the information is already in the price? If no one invests in acquiring information, how will the information be reflected in security prices in order for markets to operate efficiently? Therefore, markets cannot be efficient in their purest form with no investment in information.
Following the near-efficiency model developed by Grossman and Stiglitz, active managers search for pockets of inefficiency, hence causing the market to be nearly-efficient. Active managers earn excess returns in these pockets of inefficiency as a reward for investing and acquiring information. Generally, such pockets of inefficiency are found in illiquid market segments with poor information dissemination, and where outsized profits may be difficult to achieve.
The model developed by Grossman and Stiglitz is closely related to the risk framework of the APT developed by Ross (1976). In the multifactor model developed by Ross, active managers and arbitrageurs drive assets’ expected return towards a value in line with an equilibrium risk-return tradeoff. APT assumes that returns from the assets can be explained using systemic factors that agents wish to hedge against. These factors represent risks that cannot be arbitraged away in their purest form, and investors must be compensated for assuming this risk.
Even though markets do not appear to be perfectly efficient, substantial literature continues to investigate the Efficient Market Hypothesis (EMH). EMH implies that, since speculative trading is expensive, even with active management, investors cannot beat the market.
The EMH does have a very high benchmark: if we are average, we will hold the market portfolio and indeed be ahead simply because we are saving transaction costs. Despite our awareness that the market cannot be perfectly efficient, tests of the EMH are still vital since they allow investors to weigh where they may generate excess returns. In light of the Grossman-Stiglitz model, eagle-eyed investors can identify the pockets of inefficiency where active management efforts are most effective.
For several decades, the EMH has been refined so as to address the original shortcomings of CAPM, including imperfect information, the cost of transactions, financing, and agency. Ang, Goetzmann, and Schaefer (2011) summarizes EMH tests. It can be noted that deviations from efficiency have two forms: rational and behavioral.
From a rational point of view, high returns compensate for losses incurred during bad times. The goal is to define those bad times and determine whether these are actually bad times for an individual investor. During periods of low economic growth, certain investors benefit even though most find these periods to be unprofitable. The rational explanation for such risk premiums is that they will not disappear unless there is a total disruption of the entire economy. These premiums are scalable and suitable for very large asset owners.
In a behavioral explanation, high expected returns result from underreaction or overreaction of agents to news or events. It is also possible to develop behavioral biases either if beliefs are not updated efficiently or some information is ignored. Perfectly rational investors, who are free from these biases, should bring in enough capital to eliminate this mispricing with time. It is important to consider how quickly an asset owner can invest before the rest follow. At least, for slow-moving asset owners, a better explanation for investing is the persistence of a behavioral bias as a result of barriers to entry. Some barriers may be structural. For instance, some investors may be unable to take advantage of this investment opportunity. Investors may be required to hold certain types of assets, such as bonds with a certain credit rating, in order to comply with regulations.
Practice Question
Zara is an investment analyst working for a hedge fund that focuses on emerging markets. In a meeting with her team, she presents an in-depth analysis of a recent trend in the stock market of a developing country. She notes that this particular market seems to exhibit unusual price patterns. Some of the team members argue that these patterns are evidence of inefficiencies in the market, while others believe they are just anomalies that don’t undermine the principles of the Efficient Market Hypothesis (EMH).
Given this scenario, which of the following statements best captures the central tenets of the Efficient Market Hypothesis and its implications for this market scenario?
A. The market is always efficient, and any observed price anomalies are due to random chance or factors not yet identified.
B. The Efficient Market Hypothesis claims that all markets are inherently efficient, regardless of their development stage.
C. If the market is efficient, it implies that the observed price patterns represent all available information, but inefficiencies can arise due to various factors like behavioral biases or limitations in information flow.
D. The observed price anomalies can be exploited for guaranteed profits, as they are clear indications that the market is inefficient.
Solution
The correct answer is C.
The Efficient Market Hypothesis (EMH) posits that stock prices reflect all available information. If a market is efficient, any observed price patterns would indicate that the prices represent all known information about the stocks. However, inefficiencies can emerge due to several reasons, such as behavioral biases, limitations in information flow, or structural barriers. In the given vignette, the presence of unusual price patterns does not necessarily invalidate the principles of EMH but could point to potential inefficiencies in that particular market.
A is incorrect. While EMH argues that stock prices reflect all available information, it doesn’t assert that every observed price movement or anomaly is due to random chance. There could be various reasons for anomalies, and some may even point to inefficiencies.
B is incorrect. The EMH does not claim that all markets are inherently efficient all the time. The level of efficiency can vary based on the market, its maturity, and other factors. For instance, emerging markets might display inefficiencies more frequently than well-established markets due to reasons like less liquidity, lower transparency, or slower information dissemination.
D is incorrect. Even if a market displays anomalies or inefficiencies, it does not guarantee that these can be exploited for assured profits. There are costs, risks, and uncertainties involved in trying to capitalize on perceived inefficiencies, and the EMH does not rule out the possibility of anomalies – it simply suggests that these anomalies shouldn’t persist in a way that offers arbitrage opportunities in an efficient market.
Things to Remember
- The Efficient Market Hypothesis (EMH) asserts that stock prices reflect all available information in an efficient market.
- Efficient markets exhibit price patterns that represent all known information about stocks.
- Inefficiencies can arise due to behavioral biases, limitations in information flow, and structural barriers.
- Unusual price patterns in a market do not necessarily invalidate the principles of EMH.
- EMH’s claim of market efficiency doesn’t imply that all markets are inherently efficient at all times.
- Market efficiency can vary based on factors such as market maturity, liquidity, and transparency.