Empirical Properties of Correlation: Behaviors of Correlation in the Real World

After completing this reading, you should be able to:

• Describe how equity correlations and correlation volatilities behave throughout various economic states.
• Calculate a mean reversion rate using standard regression and calculate the corresponding autocorrelation.
• Identify the best-fit distribution for equity, bond, and default correlations.

Equity Correlations and Correlation Volatilities throughout Various Economic States

It is an open secret that the correlation between various assets changes depending on the existing economic environment. As happened in the 2007/2009 financial crisis, for example, correlations in the stock market tend to increase when hard economic times prevail. So, is there any empirical evidence that supports this assertion? We are going to look at a study conducted on stocks in the Dow Jones Industrial Average from January 1972 to October 2012.

The Dow, as it is commonly called, is a stock market index that measures the performance of some 30 stocks trading on stock exchanges in the U.S.A. Daily closing prices of the 30 stocks were observed from January 1972 to October 2012.

The process resulted in 10,303 daily observations of the Dow stocks and hence 10,303 x 30 = 309,090 closing prices. Monthly bins were built and 900 (30 * 30) correlation values for each month established, making use of the Pearson correlation approach. A simple calculation will also reveal that there were a total of 490 months in the study. This implies that in total, there were 441,000 correlation values (490 * 900). The next step involved the elimination of unity correlation values (correlations of each stock with itself). This resulted in 426,300 correlation values (441,000 – 30 * 490).

These average correlation values were then compared for three states of the U.S. economy:

• An expansionary period with gross domestic product (GDP) growth rates of 3.5% or higher (light gray zones).
• A normal economic period with growth rates between 0% and 3.49% (medium gray zones).
• A recession period with two consecutive quarters of negative growth rates (dark gray zones).

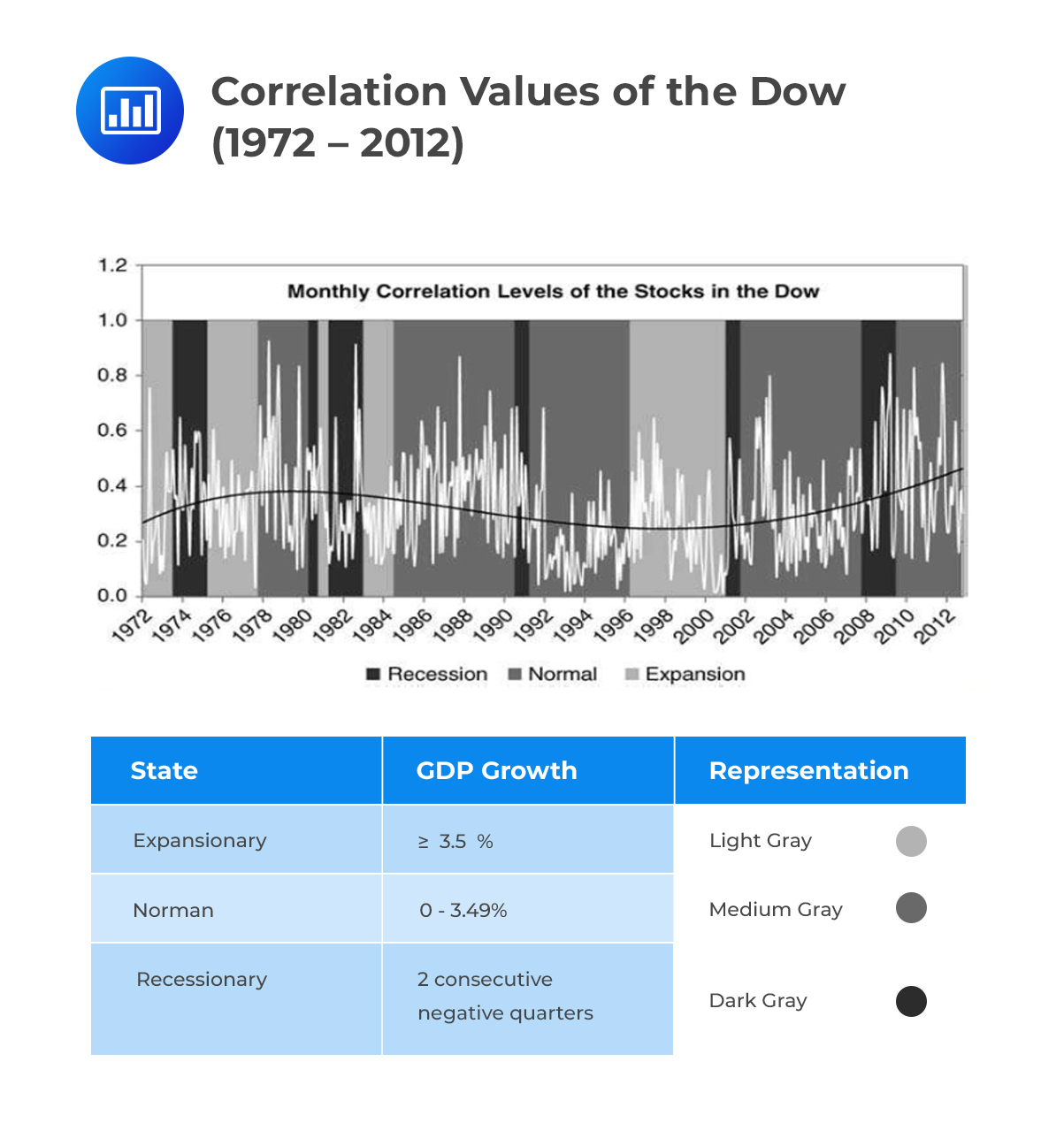On the basis of these three definitions, from 1972 to 2012, there were six recessions, five expansionary periods, and five normal periods.

The researcher then compared monthly correlation and correlation volatilities for each economic state. The exercise had some very informative results; correlation levels during a recession, normal period, and expansionary period were 37.0%, 32.7%, and 27.5%, in that order. The corresponding correlation volatilities were 80.5%, 83.4%, and 71.2%.

$$ \begin{array}{c|c|c} \textbf{Economic state} & \textbf{Correlation level} & \textbf{Correlation volatility} \\ \hline \text{Recession} & {37.0\%} & {80.5\%} \\ \hline \text{Normal} & {32.7\%} & {83.4\%} \\ \hline \text{Expansionary} & {27.5\%} & {71.2\%} \\ \end{array} $$

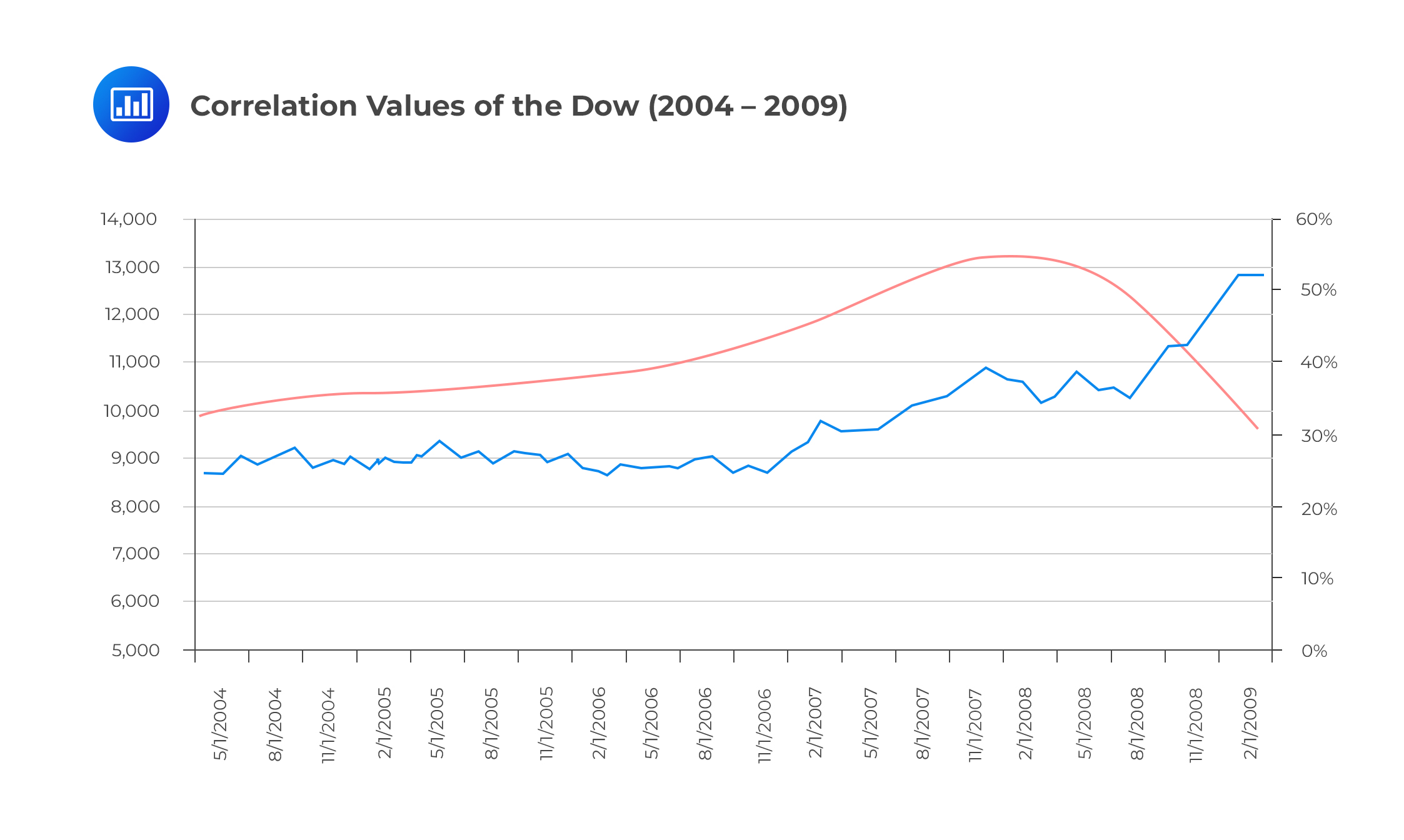
A similar study conducted on the Dow between May 2004 and March 2009 reveals very similar results. Between 2004 and 2006, the Dow increases moderately, and correlation is somewhat stable. In the time period from January 2007 to February 2008, the Dow increases more sharply, and the correlation between stocks also increases. In the time of the severe economic distress (Aug 2008 to March 2009), the Dow tumbles; we observe a sharp increase in correlations – from a meager average of 27% before the crisis to more than 50%. In fact, the correlation of the stocks hits a high of 96.97% in February 2009.

What is Our Conclusion?

1. Correlation levels are lowest in strong economic growth times (expansionary periods). This suggests that stock values rely more on company-specific information rather than macroeconomic factors.
2. Correlations are somewhat stable during normal economic conditions In such a period, the overall direction of stock markets is relatively uncertain.
3. Correlation levels are highest in weak economic growth times (recessions) During a recession, stocks tend to go down together in a market-wide fashion. The lesson here is that while formulating risk management models, risk managers should recognize the high correlation levels and correlation volatilities during times of economic distress. Correlation risk is highest during a recession.
4. Generally, a positive relationship exists between correlation level and correlation volatility

Calculate a Mean Reversion Rate Using Standard Regression

Mean reversion is the tendency of a variable to be pulled back to its long-term mean. Over time, variables or returns tend to be pulled back to the mean or average return. There’s strong empirical evidence that most financial variables exhibit mean reversion. That includes bond values, interest rates, stock returns, and credit spreads.

For example, consider a bond issued at par ($100); its price will fluctuate throughout its life in response to a number of variables such as interest rates and credit risk. If the bond does not default, it will revert to exactly that price of $100 at maturity. And this makes sense; if you’re the bond owner, you will be increasingly reluctant to sell at a discount when you know very well that you stand a chance to receive the higher par value if you see the contract out. The party on the opposite side, the buyer, won’t be ready to pay much of a premium for a bond nearing maturity because they stand to receive only the par price if the purchase is successful.

Interest rates also demonstrate a mean-reverting pattern. During an expansionary period, the demand for capital usually increases. This, in return, makes interest rates rise. At the peak of such a period, the economy undergoes overheating, paving way for a recession. At this point, the demand for capital falls, forcing lenders to reduce interest rates towards a long-term mean. In fact, interest rates might even drop below the long-term mean. (An overheating economy is one in which demand outstrips supply; the available economic resources are unable to keep pace with growing aggregate demand).

Statistical Definition

Statistically, mean reversion is present if there is a negative relationship between the change of a variable over time, \(S_t – S_{t-1}\), and the variable in the previous period, \(S_{t-1}\). So, if we express this formally, there is mean reversion if:

$$ \cfrac { \partial S_t-S_{t-1} }{\partial S_{t-1} } < 0 $$ Where:

\(S_t\) = Value of the variable at time period t.

\(S_{t-1}\) = Value of the variable in the previous time period; ∂ = partial derivative coefficient.

There will be mean reversion if \(S_{t-1}\) increases (decreases) by a small amount, causing \(S_t – S_{t-1}\) to decrease (increase) by a certain amount. We can actually try to internalize this intuitively: if \(S_{t-1}\) has decreased and is low at t -1 (relative to the mean of S, \(\mu_S\)), then at the next point in time t, mean reversion will pull up \(S_{t-1}\) to \(\mu_S\) and therefore, increase \(S_t – S_t\). if \(S_{t-1}\) has increased and is high at t -1 (relative to the mean of S, \(\mu_S\)), then at the next point in time t, mean reversion will pull down \(S_{t-1}\) to \(\mu_S\). Consequently, this will decrease \(S_t – S_t\).

The degree of reversion back to the mean or rather the degree of the pull is referred to as the mean reversion rate.

Quantifying the Degree of Mean Reversion

We demonstrate the implication of the mean reversion rate using a model used to describe the dynamic behavior of interest rates by Vasicek in his work published in 1997.

$$ S_t-S_{t-1}=\alpha(\mu_S-S_{t-1} )\Delta t+\sigma_S \epsilon \sqrt{\Delta t} $$ \(S_t\)= Price at time t.

\(S_{t-1}\)= Price at the previous point in time t-1.

\(\alpha\) = Degree of mean reversion, also called mean reversion rate or gravity, \(0 \le \alpha \le 1\).

\(\mu_S\) = Long-term mean of S.

\(\sigma_S\) = Volatility of S.

\(\epsilon\) = Standard normal shock at time t.

Since we are only interested in measuring mean reversion, we can conveniently ignore the last term, \(\sigma_S \epsilon \sqrt{\Delta t}\), which is the stochastic part of the equation requiring random samples from a distribution over time. In addition, let’s assume that \(\Delta t = 1\), so that:

$$ S_t-S_{t-1}=\alpha (\mu_S-S_{t-1} ) $$ From the equation, we can demonstrate the fact that a mean reversion rate of 1(i.e., \(\alpha\)) pulls \(S_{t-1}\) to the long-term mean \(\mu_S\) completely at every time step.

For example, if \(S_{t-1}\) is 60 and \(\mu_S\) is 100, then \(\alpha (\mu_S-S_{t-1} )=1×(100-60)=40.\)

Therefore, the \(S_{t-1}\) of 60 is mean reverted up to its long-term mean of 100.

It follows that a mean reversion parameter \(\alpha = 0.5\) will lead to a mean reversion of 50% at each time step, while a mean reversion parameter \(\alpha = 0\) will result in no mean reversion.

Estimating the Mean Reversion Rate

We can use standard regression analysis to estimate the mean reversion rate, α.

As noted earlier, the Vasicek model ignoring stochasticity is given as:

$$ S_t-S_{t-1}=\alpha (\mu_S-S_{t-1}) \Delta t $$

Now, suppose we set \(\Delta t = 1\),

We will have:

$$ \begin{align*} S_t-S_{t-1} & = \alpha (\mu_S-S_{t-1} ) \\ S_t-S_{t-1} & =\alpha \mu_S- \alpha S_{t-1} \\ \end{align*} $$

To find mean reversion rate, we run a standard regression analysis of the form:

$$ Y=a+BX $$ \(S_t-S_{t-1}=Y; \alpha \mu_S=a; -\alpha S_{t-1}=BX \) We run a regression where \(S_t-S_{t-1}\) is regressed with respect to \(S_{t-1}\). We observe that the regression coefficient B is equal to the negative mean reversion parameter \(\alpha\).

In the study conducted on stocks in the Dow Jones Industrial Average from January 1972 to October 2012, the data resulted in the following regression equation:

$$ Y = 0.2702 – 0.7751x $$ So, what does this imply? The beta coefficient of -0.7751 implies a mean reversion rate of approximately 78%. Note that this value is quite big, implying that a return to the mean correlation is tenable if there is a large increase (decrease) from the mean correlation for one month. The following month is expected to have a large decrease (increase) in correlation.

Example: Calculating the Expected Correlation

The long-term mean of the correlation data is 35.55%. In June 2012, the average correlation of the 30 × 30 Dow correlation matrices was 24.95%. A risk manager ran a regression function and came up with the following regression relationship:

$$ Y = 0.2702 – 0.7751x $$ What is the expected correlation for July 2012 given the mean reversion rate estimated in the regression analysis?

Solution

The implication here is that \(S_{t-1}\) is June and \(S_t\) is July. Hence, we should solve for \(S_t\).

Remember that $$ S_t-S_{t-1}=\alpha (\mu_S-S_{t-1} ) $$ Thus, $$ S_t=\alpha(\mu_S-S_{t-1} )+S_{t-1} = \alpha(35.55\%-24.95\%)+24.95\%=\alpha(10.6\%)+24.95\% $$ The beta coefficient of -0.7751 implies a mean reversion rate of 0.7751.

Therefore, \(S_t = 0.7751 × 10.6\% + 24.95\% = 33.17\%\)

As a result, we find that the mean reversion rate of 77.51% increases the correlation of 24.95% in June 2012 to an expected correlation of 33.17% in July 2012.

Autocorrelation

Autocorrelation is the degree to which a variable is correlated to its past values.

It is usually estimated using an autoregressive conditional heteroskedasticity (ARCH) model or a generalized autoregressive conditional heteroskedasticity (GARCH) model. It can also be estimated by running a standard regression function.

Autocorrelation is the “reverse property” to mean reversion; it has properties that are the exact opposite of mean reversion. While mean reversion measures the tendency to pull away from the current value back to the long-run mean, autocorrelation measures the persistence to pull toward more recent historical values.

The sum of the mean reversion rate and the one-period autocorrelation rate will always equal one. So if we have a mean reversion of 78%, then the autocorrelation is 22%. The stronger the mean reversion, the lower the autocorrelation and vice versa.

We derive the autocorrelation (AC) for a time lag of one period as:

$$ \text{AC}(\rho_t,\rho_{t-1} )=\cfrac {\text{Cov}(\rho_t,\rho_{t-1}) }{\sigma (\rho_t )\sigma(\rho_{t-1})} $$ where:

• \(\text{AC}(\rho_t,\rho_{t-1} )\) = Autocorrelation of the correlation from time period t and the correlation from time period t – 1.
• \(\rho_t\) = Correlation values for time period t.
• \(\rho_{t-1}\) = Correlation values for time period t -1 [In our study on the Dow, for example, \(\rho_t\) represents the correlation matrix for Dow stocks on day t, and \(\rho_{t-1}\) represents the correlation matrix for Dow stocks on day t – 1].
• \(\text{Cov}(\rho_t,\rho_{t-1} )\) = Covariance between the correlation measures [We determine the covariance between correlations the same way we determine covariance for equity returns].

From the correlation data collected on the Dow from January 1972 to October 2012, we can use the autocorrelation formula above and determine the one-period lag autocorrelation of Dow stocks for the period. A correct computation process would give a value of 22%. To arrive at this answer, we subtract the mean reversion rate from one.

The Best-fit Distribution for Equity, Bond, and Default Correlations

Equity Correlations

We again analyze the results of the study conducted on (30) stocks in the Dow Jones Industrial Average from January 1972 to October 2012. Remember that after eliminating unity correlation values (correlations of each stock with itself) there were 426,300 correlation values.

• Mostly positive correlations between the stocks in the Dow were observed, with 77.23% of all 426,300 correlation values being positive.
• The researcher tested 61 distributions for fitting the histogram, applying three standard fitting tests: (1) Kolmogorov-Smirnov, (2) Anderson Darling, and (3) chi-squared. The versatile Johnson SB distribution provided the best fit with four parameters: two for the shape, one for location, and one for scale. The more common distributions such as the normal, lognormal, and beta distributions provided a poor fit for equity correlations.
• As noted earlier, there were six recessions in the 40-year period from 1972 to 2012. The most severe recession for this time period occurred from 2007 to 2009 following the global financial crisis. The percentage change in correlation volatility prior to five out of the six recessions was negative. These findings strongly suggest that correlation volatility is low during expansionary periods which often precede recessions.

Bond Correlations and Default Probabilities

A study was conducted on an assortment of bonds in an attempt to establish the correlations among them. In the study, 7,645 bond correlations and 4,655 default probability correlations displayed properties similar to those of equity correlations.

• The average correlation was 42%.
• Correlation volatility for bond correlations was 64%.
• Bond correlations were found to exhibit some mean reversion, but the mean reversion was just 26%, significantly lower than that of stocks (78%).
• The generalized extreme value (GEV) distribution was found to be the best fit distribution for bond correlations. However, the normal distribution was also found to be a good fit for bond correlations.
• A study of 4,633 default probability correlations revealed an average default correlation of 30%.
• Correlation volatility for default probability correlations was 88%.
• Default probability correlations were found to exhibit some mean reversion, with a mean reversion rate of 30%.
• The default probability correlation distribution was found to be similar to the equity correlation distribution and was replicated best by the Johnson SB distribution.

$$ \begin{array} {c|c|c} \textbf{Correlation type} & \textbf{Average } & \textbf{Correlation } & \textbf{Best fit} \\ {} & \textbf{correlation} & \textbf{volatility} & \textbf{distribution} \\\hline \text{Equity} & {35\%} & {80\%} & \text{Johnson SB} \\ \hline \text{Bond} & {42\%} & {64\%} & \text{Generalized } \\ {} & {} & {} & \text{Extreme Value} \\ \hline \text{Default Probability} & {30\%} & {88\%} & \text{Johnson SB} \\ \end{array} $$

Summary

• Equity correlations increase as the economy declines. Equity correlations were extremely high in the Great Recession of 2007 to 2009, hitting a record 96.97% in February 2009.
• Correlation levels are lowest in strong economic growth times (expansionary periods). This suggests that stock values rely more on company-specific information rather than macroeconomic factors.
• Correlations are somewhat stable during normal economic conditions. In such a period, the overall direction of the stock markets is relatively uncertain.
• Correlation levels are highest in weak economic growth times (recessions). During a recession, stocks tend to go down together in a market-wide fashion. The lesson here is that while formulating risk management models, risk managers should be conscious of the high correlation levels and correlation volatilities during times of economic distress. Correlation risk is highest during a recession.
• Generally, a positive relationship exists between correlation level and correlation volatility.
• Since equity correlations display strong mean reversion, they display low autocorrelation.
• The sum of the mean reversion rate and the one-period autocorrelation rate will always equal one.
• Equity correlations show a very strong mean reversion. Mean reversion should be included in equity correlation models.
• Bond correlation levels and bond correlation volatilities are generally higher in bad economic times. What’s more, bond correlations exhibit mean reversion, although lower mean reversion than equity correlations exhibit.
• Default correlations also exhibit properties seen in equity correlations. Default probability correlation levels are slightly lower than equity correlation levels, and default probability correlation volatilities are slightly higher than equity correlations.

Question 1

Correlation data has a long-term mean of 43.6%. The averaged correlation was observed as 41.32% in June 2014 for the 30 x 30 Dow correlation matrices. Given that the average mean reversion was 79.1% from the regression function for 40 years, determine the expected correlation one month later. What is the implication?

1. 42.69%.
2. 43.12%.
3. 39.51%.
4. 42.98%.

The correct answer is B.

Using equation:

$$ { S }_{ t }-{ S }_{ t-1 }=a{ \mu }_{ s }-a{ S }_{ t-1 } $$

Then:

$$ { S }_{ t }=a\left( { \mu }_{ s }-{ S }_{ t-1 } \right) +{ S }_{ t-1 } $$

Where:

\(a\) = 79.1%.

\({ \mu }_{ s }\) = 43.6%.

\({ S }_{ t-1 }\) = 41.32%.

Therefore,

$$ { S }_{ t }=0.791\left( 0.436–0.4132 \right) +0.4132 = 0.4312 = 43.12\% $$

The mean reversion rate of 79.1% increases correlation of 41.32% in June 2014 to an expected correlation of 43.12% in July 2014.

Question 2

Jenna, an experienced risk manager at Blackbird Asset Management, is discussing with her team the implications of equity correlations and correlation volatilities in different economic states. Which of the following statements is correct?

A. Equity correlations remain consistent across different economic states, while correlation volatilities decrease during economic downturns.

B. Equity correlations and correlation volatilities both decrease in economic downturns, leading to more robust portfolio diversification.

C. Equity correlations tend to increase during economic downturns, leading to decreased diversification benefits, while correlation volatilities also tend to rise, adding to uncertainty.

D. Equity correlations decrease during economic downturns, while correlation volatilities remain consistently high regardless of the economic state.

Solution

The correct answer is C.

It is generally observed that during economic downturns or periods of market stress, equity correlations tend to increase. This means that assets move more closely together, and the benefits of portfolio diversification decrease. Additionally, the volatility of correlations, or how much correlations change, also tends to increase during these times, adding another layer of uncertainty and risk.

A is incorrect because equity correlations do not remain consistent across different economic states. In fact, they tend to increase during economic downturns. Moreover, correlation volatilities do not decrease during downturns; they often increase.

B is incorrect because it falsely suggests that equity correlations and correlation volatilities both decrease in downturns. In reality, both tend to increase during such times, which can adversely impact portfolio diversification strategies.

D is incorrect because it inaccurately claims that equity correlations decrease during economic downturns. The general consensus is that they increase during such periods. The statement about correlation volatilities remaining consistently high is also misleading; their behavior can vary based on market conditions and economic states.

Things to Remember

• Equity correlations depict how closely asset returns move together.
• During economic downturns or periods of market stress, equity correlations usually rise. This means assets tend to move in a more similar manner, diminishing the benefits of portfolio diversification.
• Correlation volatility represents the variability of correlations over time.
• Correlation volatilities also tend to increase during economic downturns, introducing another dimension of risk and uncertainty.
• Increased equity correlations and correlation volatilities during market stress challenge traditional portfolio diversification strategies.