Nonstationary Time Series
After completing this reading, you should be able to: Describe linear and nonlinear... Read More
After completing this reading, you should be able to:
A return is a profit from an investment. Two common methods used to measure returns include:
Denoted \(\text R_{\text t}\) the simple return is given by:
$$ \text R_{\text t}=\cfrac {\text P_{\text t}-\text P_{\text t-1}}{\text P_{\text t-1}} $$
Where
\(\text P_{\text t}\)=Price of an asset at time t (current time)
\(\text P_{\text t-1}\)=Price of an asset at time t-1 (past time)
The time scale is arbitrary or shorter period such monthly or quarterly. Under the simple returns method, the returns over multiple periods is the product of the simple returns in each period. Mathematically given by:
$$ \begin{align*} 1+\text R_{\text T}& = \prod_{\text t=\text i}^{\text T} (1+\text R_{\text t}) \\ ⇒\text R_{\text T} & = \left(\prod_{\text t=\text i}^{\text T} (1+\text R_{\text t}) \right)-1 \\ \end{align*} $$
Consider the following data.
$$ \begin{array}{c|c} \textbf{Time} & \textbf{Price} \\ \hline {0} & {100} \\ \hline {1} & {98.65} \\ \hline {2} & {98.50} \\ \hline {3} & {97.50} \\ \hline {4} & {95.67} \\ \hline {5} & {96.54} \\ \end{array} $$
Calculate the simple return based on the data for all periods.
We need to calculate the simple return over multiple periods which is given by:
$$ 1+\text R_{\text T}= \prod_{\text t=\text i}^{\text T} (1+\text R_{\text t}) $$
Consider the following table:
$$ \begin{array}{c|c} \textbf{Time} & \textbf{Price} & \bf{\text R_{\text t}} & \bf{1+\text R_{\text t}} \\ \hline {0} & {100} & {-} & {-} \\ \hline {1} & {98.65} & {-0.0135} & {0.9865} \\ \hline {2} & {98.50} & {-0.00152} & {0.998479} \\ \hline {3} & {97.50} & {-0.01015} & {0.989848} \\ \hline {4} & {95.67} & {-0.01877} & {0.981231} \\ \hline {5} & {96.54} & {0.009094} & {1.009094} \\ \hline {} & {} & \textbf{Product} & \bf{0.9654} \\ \end{array} $$
Note that
$$ \text R_{\text t}=\cfrac {\text P_{\text t}-\text P_{\text t-1}}{\text P_{\text t-1}} $$
So that that
$$ \text R_1=\cfrac {\text P_1-\text P_0}{\text P_0} =\cfrac {98.65-100}{100}=-0.0135 $$
And
$$ \text R_2=\cfrac {\text P_2-\text P_1}{\text P_1} =\cfrac {98.50-98.65}{98.65}=-0.00152 $$
And so on.
Also note that:
$$ \prod_{\text t=1}^5 (1+ \text R_{\text t} )=0.9865×0.998479×…×1.009094=0.9654 $$
So,
$$ 1+\text R_{\text T}=0.9654 \Rightarrow \text R_{\text T}=-0.0346=-3.46\% $$
Denoted by \(\text r_{\text t}\). Compounded returns is the difference between the natural logarithm of the price of assets at time t and t-1. It is given by:
$$ \text r_{\text t}=\text {ln } \text P_{\text t}-\text {ln} \text P_{\text t-1} $$
Computing the compounded returns over multiple periods is easy because it is just the sum of returns of each period. That is:
$$ \text r_{\text T}=\sum_{\text t=1}^{\text T} \text r_{\text t} $$
Consider the following data.
$$ \begin{array}{c|c} \textbf{Time} & \textbf{Price} \\ \hline {0} & {100} \\ \hline {1} & {98.65} \\ \hline {2} & {98.50} \\ \hline {3} & {97.50} \\ \hline {4} & {95.67} \\ \hline {5} & {96.54} \\ \end{array} $$
What is the continuously compounded return based on the data over all periods?
Solution
The continuously compounded return over the multiple periods is given by
$$ \text r_{\text T}=\sum_{\text t=1}^{\text T} \text r_{\text t} $$
Where
$$ \text r_{\text t}=\text{ln } \text P_{\text t}-\text{ln }\text P_{\text t-1} $$
Consider the following table:
$$ \begin{array}{c|c|c} \textbf{Time} & \textbf{Price} & \bf{\text r_{\text t}=\text{ln } \text P_{\text t}-\text{ln }\text P_{\text t-1}} \\ \hline {0} & {100} & {-} \\ \hline {1} & {98.65} & {-0.01359} \\ \hline {2} & {98.50} & {-0.00152} \\ \hline {3} & {97.50} & {0.0102} \\ \hline {4} & {95.67} & {-0.01895} \\ \hline {5} & {96.54} & {0.009053} \\ \hline {} & \textbf{Sum} & \bf{-0.03521} \\ \end{array} $$
Note that
$$ \begin{align*} \text r_1 & =\text {ln } \text P_1 -\text {ln } \text P_0=\text {ln }98.65-\text {ln }100=-0.01359 \\ \text r_2 & =\text {ln } \text P_2 -\text {ln } \text P_1 =\text {ln }98.50-\text {ln }98.65=-0.00152 \\ \end{align*} $$
And so on.
Also,
$$ \text r_{\text T}=\sum_{\text t=1}^{5} \text r_{\text t}=-0.01359+-0.00152+⋯+0.009053=-0.03521=-3.521\% $$
Intuitively, the compounded returns is an approximation of the simple return. The approximation, however, is prone to significant error over longer time horizons, and thus compounded returns are suitable for short time horizons.
The relationship between the compounded returns and the simple returns is given by the formula:
$$ 1+\text R_{\text t}=\text e^{\text r_{\text t} } $$
What is the equivalent simple return for a 30% continuously compounded return?
Solution.
Using the formula:
$$ \begin{align*} 1+\text R_{\text t} & =\text e^{\text r_{\text t} } \\ \Rightarrow \text R_{\text t} & =\text e^{\text r_{\text t} }-1=\text e^0.3-1=0.3499=34.99\% \\ \end{align*} $$
It is worth noting that compound returns are always less than the simple return. Moreover, simple returns are never less than -100%, unlike compound returns, which can be less than -100%. For instance, the equivalent compound return for -65% simple return is:
$$ {\text r_{\text t} }=\text{ln }(1-0.65)=-104.98\% $$
The volatility of a variable denoted as \(\sigma\) is the standard deviation of returns. The standard deviation of returns measures the volatility of the return over the time period at which it is captured.
Consider the linear scaling of the mean and variance over the period at which the returns are measured. The model is given by:
$$ \text r_{\text t}=\mu+\sigma \text e_{\text t} $$
Where \(\text E(\text r_{\text t} )=\mu\) is the mean of the return, \(\text V(\text r_{\text t} )=\sigma^2\) is the variance of the return. \( \text e_{\text t}\) is the shocks, which is assumed to be iid distributed with the mean 0 and variance of 1. Moreover, the return is assumed to be also iid and normally distributed with the mean \(\mu^2\) i.e. \(\text r_{\text t} {\sim}^{iid} \text N(\mu,\sigma^2)\). Note the shock can also be expressed as \(\epsilon_{\text t}=\sigma \text e_{\text t}\) where: \(\epsilon_{\text t}\sim \text N(0,\sigma^2)\).
Assume that we wish to calculate the returns under this model for 10 working days (two weeks). Since the model deals with the compound returns, we have:
$$ \sum_{\text i=1}^{10} {\text r}_{\text t+\text i }=\sum_{\text i=1}^{10} (\mu+\sigma \text e_{\text t+\text i})=10\mu +\sigma \sum_{\text i=1}^{10} \text e_{\text t+\text i} $$
So that the mean of the return over the 10 days is \(10 \mu\) and the variance also is \(10\sigma^2\) since \(\text e_{\text t}\) is iid. The volatility of the return is, therefore:
$$ \sqrt{10}\sigma $$
Therefore, the variance and the mean of return are scaled to the holding period while the volatility is scaled to the square root of the holding period. This feature allows us to convert volatility between different periods.
For instance, given daily volatility, we would to have yearly (annualized) volatility by scaling it by \(\sqrt{252}\). That is:
$$ \sigma_{\text{annual}}=\sqrt{252×\sigma_{\text{daily}}^2} $$
Note that 252 is the conventional number of trading days in a year in most markets.
The monthly volatility of the price of gold is 4% in a given year. What is the annualized volatility of the gold price?
Using the scaling analogy, the corresponding annualized volatility is given by:
$$ \sigma_{\text{annual}}=\sqrt{12×0.04^2 }=13.86\% $$
The variance rate, also termed as variance, is the square of volatility. Similar to mean, variance rate is linear to holding period and hence can be converted between periods. For instance, an annual variance rate from a monthly variance rate is given by
$$ \sigma_{\text{annual}}^2=12×\sigma_{\text{monthly}}^2 $$
The variance of returns can be approximated as:
$$ {\hat \sigma}^2=\cfrac {1}{\text T} \sum_{\text t-1}^{\text T}(\text r_{\text t}-{\hat \mu})^2 $$
Where \({\hat \mu}\) is the sample mean of return, and T is the sample size.
The investment returns of a certain entity for five consecutive days is 6%, 5%, 8%,10% and 11%. What is the variance estimator of returns?
We start by calculating the sample mean:
$$ \hat \mu=\cfrac {1}{5} (0.06+0.05+0.08+0.10+0.11)=0.08 $$
So that the variance estimator is:
$$ {\hat \sigma}^2=\cfrac {1}{\text T} \sum_{\text t-1}^{\text T}(\text r_{\text t}-\hat \mu)^2 $$
$$ =\cfrac {1}{5} \left[(0.06-008)^2+(0.05-0.08)^2+(0.08-0.08)^2+(0.10-0.08)^2+(0.11-0.08)^2 \right]=0.00052=0.052\% $$
Implied volatility is an alternative measure of volatility that is constructed using options valuation. The options (both put and call) have payouts that are nonlinear functions of the price of the underlying asset. For instance, the payout from the put option is given by:
$$ \text{max}(\text K-\text P_{\text T}) $$
where \(\text P_{\text T}\) is the price of the underlying asset, K being the strike price, and T is the maturity period. Therefore, the price payout from an option is sensitive to the variance of the return on the asset.
The Black-Scholes-Merton model is commonly used for option pricing valuation. The model relates the price of an option to the risk-free rate of interest, the current price of the underlying asset, the strike price, time to maturity, and the variance of return.
For instance, the price of the call option can be denoted by:
$$ \text C_{\text t}=\text f(\text r_{\text f},\text T,\text P_{\text t},\sigma^2) $$
Where:
\(\text r_{\text f}\)= Risk-free rate of interest
T=Time to maturity
\(\text P_{\text t}\)=Current price of the underlying asset
\(\sigma^2\)=Variance of the return
The implied volatility σ relates the price of an option with the other three parameters. The implied volatility is an annualized value and does not need to be converted further.
The volatility index (VIX) measures the volatility in the S&P 500 over the coming 30 calendar days. VIX is constructed from a variety of options with different strike prices. VIX applies to a large variety of assets such as gold, but it is only applicable to highly liquid derivative markets and thus not applicable to most financial assets.
The financial returns are assumed to follow a normal distribution. Typically, a normal distribution is thinned-tailed, does not have skewness and excess kurtosis. The assumption of the normal distribution is sometimes not valid because a lot of return series are both skewed and mostly heavy-tailed.
To determine whether it is appropriate to assume that the asset returns are normally distributed, we use the Jarque-Bera test.
Jarque-Bera test tests whether the skewness and kurtosis of returns are compatible with that of normal distribution.
Denoting the skewness by S and kurtosis by k, the hypothesis statement of the Jarque-Bera test is stated as:
\(\text H_0:\text S=0\) and k=3 (the returns are normally distributed)
vs
\(\text H_1:\text S\neq 0\) and \(k\neq 3\) (the returns are not normally distributed)
The test statistic (JB) is given by:
$$ { JB }=(T-1)\left( \cfrac { \hat { \text S } ^{ 2 } }{ 6 } +\cfrac { ({ \hat { \text k } }-3)^{ 2 } }{ 24 } \right) $$
Where T is the sample size.
The basis of the test is that, under normal distribution, the skewness is asymptotically normally distributed with the variance of 6 so that the variable \(\frac {{\hat {\text S}}^2}{6}\) is chi-squared distributed with one degree of freedom \((\chi_1^2)\) and kurtosis is also asymptotically normally distributed with the mean of 3 and variance of 24 so that \(\cfrac { ({ \hat { \text k } }-3)^{ 2 } }{ 24 }\) is also \((\chi_1^2)\) variable. Coagulating these arguments given that these variables are independent, then:
$$ \text{JB}\sim \chi_2^2 $$
When the test statistic is greater than the critical value, then the null hypothesis is rejected. Otherwise, the alternative hypothesis is true. We use the \(\chi_2^2\) table with the appropriate degrees of freedom:
$$\textbf{ Chi-square Distribution Table}$$
$$\begin{array}{l|ccccccccc}\hline \textbf{d.f.} & .995 & .99 & .975 & .95 & .9 & .1 & .05 & .025 & .01 \\ \hline 1 & 0.00 & 0.00 & 0.00 & 0.00 & 0.02 & 2.71 & 3.84 & 5.02 & 6.63 \\ 2 & 0.01 & 0.02 & 0.05 & 0.10 & 0.21 & 4.61 & 5.99 & 7.38 & 9.21 \\ 3 & 0.07 & 0.11 & 0.22 & 0.35 & 0.58 & 6.25 & 7.81 & 9.35 & 11.34 \\ 4 & 0.21 & 0.30 & 0.48 & 0.71 & 1.06 & 7.78 & 9.49 & 11.14 & 13.28 \\ 5 & 0.41 & 0.55 & 0.83 & 1.15 & 1.61 & 9.24 & 11.07 & 12.83 & 15.09 \\ 6 & 0.68 & 0.87 & 1.24 & 1.64 & 2.20 & 10.64 & 12.59 & 14.45 & 16.81 \\ 7 & 0.99 & 1.24 & 1.69 & 2.17 & 2.83 & 12.02 & 14.07 & 16.01 & 18.48 \\ 8 & 1.34 & 1.65 & 2.18 & 2.73 & 3.49 & 13.36 & 15.51 & 17.53 & 20.09 \\ 9 & 1.73 & 2.09 & 2.70 & 3.33 & 4.17 & 14.68 & 16.92 & 19.02 & 21.67 \\ 10 & 2.16 & 2.56 & 3.25 & 3.94 & 4.87 & 15.99 & 18.31 & 20.48 & 23.21 \\ 11 & 2.60 & 3.05 & 3.82 & 4.57 & 5.58 & 17.28 & 19.68 & 21.92 & 24.72 \\ 12 & 3.07 & 3.57 & 4.40 & 5.23 & 6.30 & 18.55 & 21.03 & 23.34 & 26.22 \end{array}$$
For example, the critical value of a \(\chi_2^2\) at a 5% confidence level is 5.991, and thus, if the computed test statistic is greater than 5.991, the null hypothesis is rejected.
Investment return is such that it has a skewness of 0.75 and a kurtosis of 3.15. If the sample size is 125, what is the JB test statistic? Does the data qualify to be normally distributed at a 95% confidence level?
The test statistic is given by:
$$ \text{JB}=(\text T-1) \left(\cfrac {{\hat {\text S}}^2}{6}+\cfrac {({\hat {\text k}}-3)^2}{24}\right)=(125-1)\left(\cfrac {0.75^2}{6}+\cfrac {(3.15-3)^2}{24} \right)=11.74 $$
Since the test statistic is greater than the 5% critical value (5.991), then the null hypothesis that the data is normally distributed is rejected.
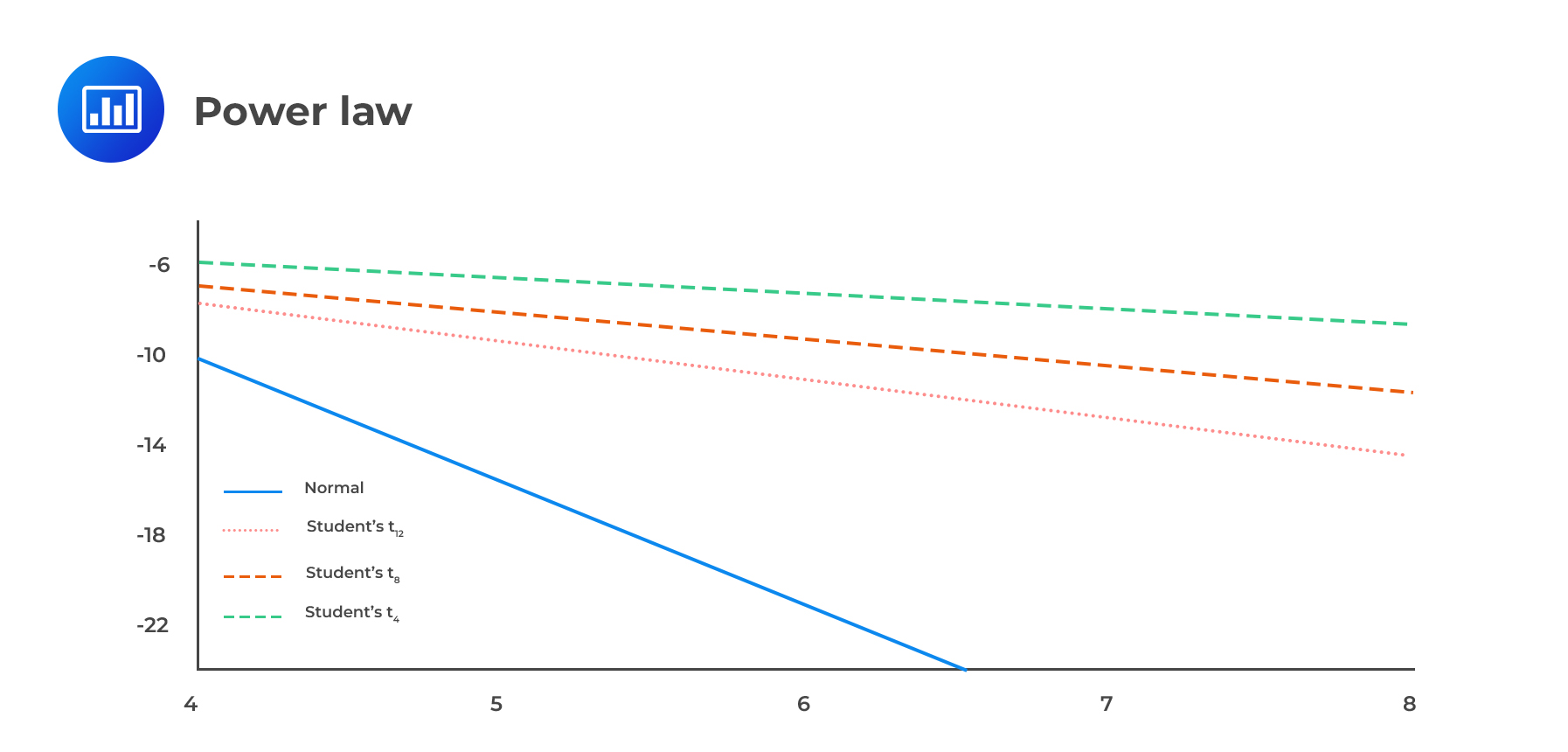
The power law is an alternative method of determining whether the returns are normal or not by studying the tails. For a normal distribution, the tail is thinned, such that the probability of any return greater than \(\text k\sigma\) decreases sharply as k increases. Other distributions are such that their tails decrease relatively slowly, given a large deviation.
The power law tails are such that, the probability of observing a value greater than a given value x defined as:
$$ \text P(\text X> \text x)=\text {kx}^{-\alpha } $$
Where k and \(\alpha\) are constants.
The tail behavior of distributions is effectively compared by considering the natural log (ln(P(X>x))) of the tail probability. From the above equation:
$$ \text{ln } \text{prob}(\text X > \text x)=\text {ln k}-\alpha \text{ln x} $$
To test whether the above equation holds, a graph of \(\text{ln } \text{prob}(\text X > \text x)\) plotted against lnx.
For a normal distribution, the plot is quadratic in x, and hence it decays quickly, meaning that they have thinned tails. For other distributions such as Student’s t distribution, the plots are linear to x, and thus, the tails decay at a slow rate, and hence they have fatter tails (produce values that are far from the mean).
 Dependence and Correlation of Random Variables.
Dependence and Correlation of Random Variables.The two random variables X and Y are said to be independent if their joint density function is equal to the product of their marginal distributions. Formally stated:
$$ \text f_{\text X,\text Y}=\text f_{\text X} (\text x).\text f_{\text Y} (\text y) $$
Otherwise, the random variables are said to be dependent. The dependence of random variables can be linear or nonlinear.
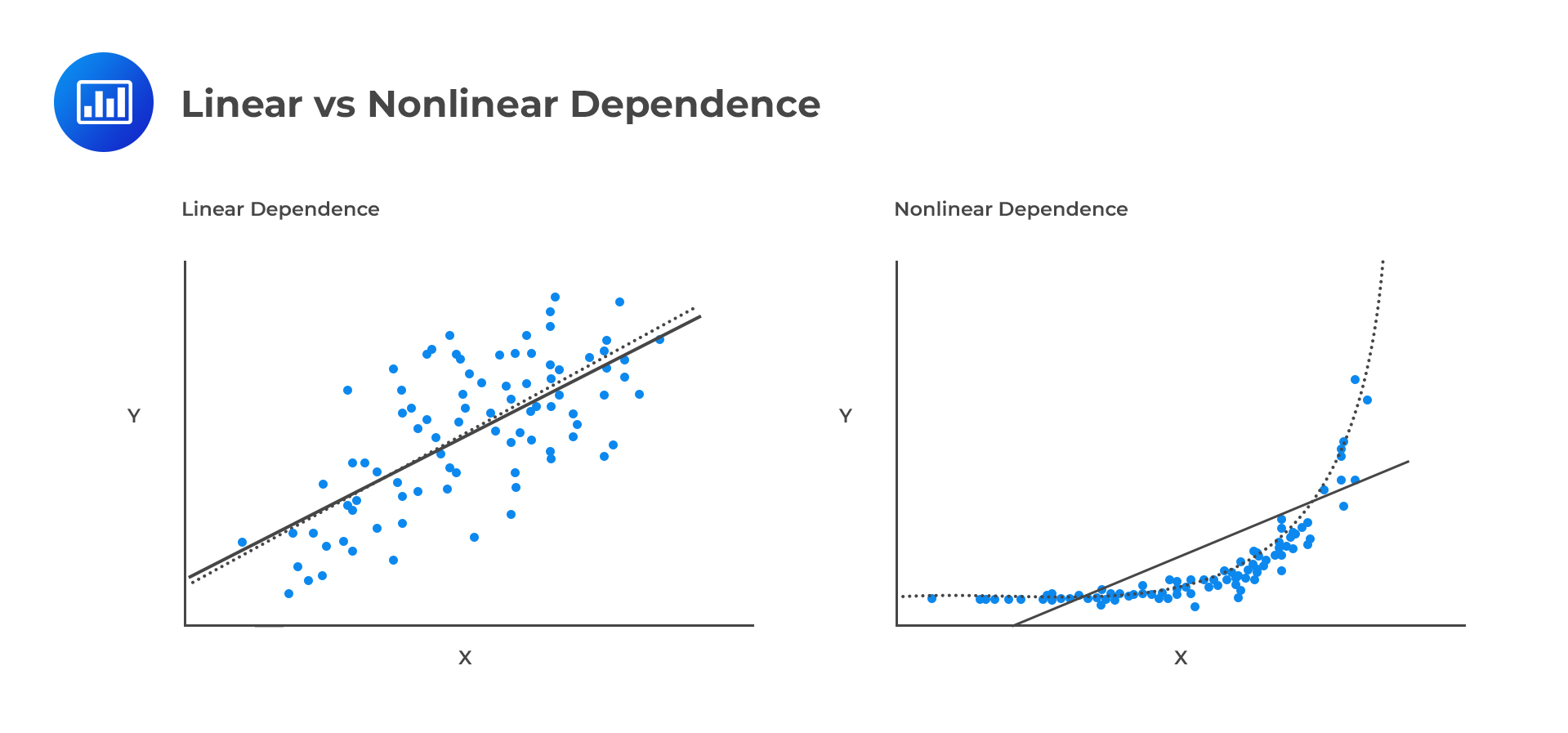 The linear relationship of the random variables is measured using the correlation estimator called Pearson’s correlation.
The linear relationship of the random variables is measured using the correlation estimator called Pearson’s correlation.
Recall that given the linear equation:
$$ \text Y_{\text i}=\alpha+\beta_{\text i} \text X_{\text i}+\epsilon_{\text i} $$
The slope \(\beta\) is related to the correlation coefficient \(\rho\). That is, if \(\beta=0\), then the random variables \(\text X_{\text i}\) and \(\text Y_{\text i}\) are uncorrelated. Otherwise, \(\beta \neq 0\). Infact, if the variances of the random variables are engineered such that they are both equal to unity \((\sigma_{\text X}^2=\sigma_{\text Y}^2=1)\), the slope of the regression equation is equal to the correlation coefficient \((\beta=\rho)\). Thus, the regression equation reflects how the correlation measures the linear dependence.
Nonlinear dependence is complex and thus cannot be summarized using a single statistic.
The correlation is mostly measured using the rank correlation (Spearman’s rank correlation) and Kendal’s τ correlation coefficient. The values of the correlation coefficient are between -1 and 1. When the value of the correlation coefficient is 0, then the random variables are independent; otherwise, a positive (negative) correlation indicates an increasing (a decreasing) relationship between the random variables.
The rank correlation uses the ranks of observations of random variables X and Y. That is, rank correlation depends on the linear relationship between the ranks rather than the random variables themselves.
The ranks are such that 1 is assigned to the smallest value, 2 to the next value, and so on until the largest value is assigned n.
When a rank repeats itself, an average is computed depending on the number of repeated variables, and each is assigned the averaged rank. Consider the ranks 1,2,3,3,3,4,5,6,7,7. Rank 3 is repeated three times, and rank 7 is repeated two times. For the repeated 3’s, the averaged rank is \(\frac {(3+4+5)}{3}=4\). For the repeated 7’s the averaged rank is \(\frac {(9+10)}{2}=8.5\). Note that we are averaging the ranks, which the repeated ranks could have to assume if they were not repeated. So the new ranks are:1,2,4,4,4,4,5,6,8.5,8.5.
Now, denote the rank of X by \(\text R_{\text X}\) and that of Y by \(\text R_{\text Y}\) then the rank correlation estimator is given by:
$$ \hat \rho_{\text s}=\cfrac {\text{Cov} (\widehat{\text R_{\text X},\text R_{\text Y}})}{ \sqrt{\hat {\text V}(R_X)} \sqrt{\hat {\text V} (\text R_{\text Y})}} $$
Alternatively, when all the ranks are distinct (no repeated ranks), the rank correlation estimator is estimated as:
$$ \hat \rho_{\text s}=1-\cfrac {6\sum_{\text i=1}^{\text n}\left(\text R_{\text X_{\text i} }-\text R_{\text Y_{\text i}} \right)^2.}{{\text n(\text n^2-1)}} $$
The intuition of the last formula is that when a highly ranked value of X is paired with corresponding ranked values of Y, then the value of \(\text R_{\text X_{\text i} }-\text R_{\text Y_{\text i}}\) is very small and thus, correlation tends to 1. On the other, if the smaller rank values of X are marched with larger rank values of Y, then \(\text R_{\text X_{\text i} }-\text R_{\text Y_{\text i}}\) is relatively larger and thus, correlation tends to -1.
When the variables X and Y have a linear relationship, linear and rank, correlations have equal value. However, rank correlation is inefficient compared to linear correlation and only used for confirmational checks. On the other hand, rank correlation is insensitive to outliers because it only deals with the ranks and not the values of X and Y.
Consider the following data.
$$ \begin{array}{c|c|c} \textbf{i} & \textbf{X} & \textbf{Y} \\ \hline {1} & {0.35} & {2.50} \\ \hline {2} & {1.73} & {6.65} \\ \hline {3} & {-0.45} & {-2.43} \\ \hline {4} & {-0.56} & {-5.04} \\ \hline {5} & {4.03} & {3.20} \\ \hline {6} & {3.21} & {2.31} \\ \end{array} $$
What is the value of rank correlation?
Consider the following table where the ranks of each variable have been filled and the square of their difference in ranks.
$$ \begin{array}{c|c|c|c|c|c} \textbf{i} & \textbf{X} & \textbf{Y} & \bf{\text R_{\text X}} & \bf{\text R_{\text Y}} & \bf{(\text R_{\text X}-\text R_{\text Y})^2} \\ \hline{1} & {0.35} & {2.50} & {3} & {4} & {1} \\ \hline {2} & {1.73} & {6.65} & {4} & {6} & {4} \\ \hline {3} & {-0.45} & {-2.43} & {2} & {2} & {0} \\ \hline {4} & {-0.56} & {-5.04} & {1} & {1} & {0} \\ \hline {5} & {4.03} & {3.20} & {6} & {5} & {1} \\ \hline {6} & {3.21} & {2.31} & {5} & {3} & {4} \\ \hline {} & {} & {} & {} & \text{Sum} & {10} \\ \end{array} $$
Since there are no repeated ranks, then the rank correlation is given by:
$$ \begin{align*} \hat \rho_{\text s}& =1-\cfrac {6\sum_{\text i=1}^{\text n}\left(\text R_{\text X_{\text i} }-\text R_{\text Y_{\text i}} \right)^2.}{{\text n(\text n^2-1)}} \\ & =1-\cfrac {6×10}{6(6^2-1)} =1-0.2857=0.7143 \\ \end{align*} $$
Kendall’s Tau is a non-parametric statistic used to measure the strength and direction of association between two random variables, say \( X \) and \( Y \). It is especially useful for ordinal or ranked data and evaluates the degree to which the relationship between two variables is monotonic.
Kendall’s \(\tau\) compares the number of concordant and discordant pairs of observations:
Kendall’s Tau is calculated using the formula:
\[
\tau = \frac{C – D}{\binom{n}{2}} = \frac{C – D}{\frac{n(n-1)}{2}}
\]
Where:
Consider the following data (same as the example above).
$$ \begin{array}{c|c|c} \textbf{i} & \textbf{X} & \textbf{Y} \\ \hline {1} & {0.35} & {2.50} \\ \hline {2} & {1.73} & {6.65} \\ \hline {3} & {-0.45} & {-2.43} \\ \hline {4} & {-0.56} & {-5.04} \\ \hline {5} & {4.03} & {3.20} \\ \hline {6} & {3.21} & {2.31} \\ \end{array} $$
What is Kendall’s \(\tau\) correlation coefficient?
Solution
We are given the following paired data:
\[\begin{array}{c|c|c}
i & X_i & Y_i \\ \hline
1 & 0.35 & 2.50 \\
2 & 1.73 & 6.65 \\
3 & -0.45 & -2.43 \\
4 & -0.56 & -5.04 \\
5 & 4.03 & 3.20 \\
6 & 3.21 & 2.31 \end{array}\]
We compute Kendall’s tau using the formula:
\[
\tau = \frac{C – D}{\binom{n}{2}} = \frac{C – D}{\frac{n(n-1)}{2}}
\]
Where:
Step 1: List All Pairs and Determine Concordance
We now examine each pair \( (i,j) \) for \( i < j \). A pair is:
\[
\begin{array}{c|c|c|c|c|c}
\text{Pair} & (X_i, Y_i) & (X_j, Y_j) & X_i – X_j & Y_i – Y_j & \text{Type} \\
\hline
(1,2) & (0.35, 2.50) & (1.73, 6.65) & -1.38 & -4.15 & \text{Concordant} \\
(1,3) & (0.35, 2.50) & (-0.45, -2.43) & 0.80 & 4.93 & \text{Concordant} \\
(1,4) & (0.35, 2.50) & (-0.56, -5.04) & 0.91 & 7.54 & \text{Concordant} \\
(1,5) & (0.35, 2.50) & (4.03, 3.20) & -3.68 & -0.70 & \text{Concordant} \\
(1,6) & (0.35, 2.50) & (3.21, 2.31) & -2.86 & 0.19 & \text{Discordant} \\
(2,3) & (1.73, 6.65) & (-0.45, -2.43) & 2.18 & 9.08 & \text{Concordant} \\
(2,4) & (1.73, 6.65) & (-0.56, -5.04) & 2.29 & 11.69 & \text{Concordant} \\
(2,5) & (1.73, 6.65) & (4.03, 3.20) & -2.30 & 3.45 & \text{Discordant} \\
(2,6) & (1.73, 6.65) & (3.21, 2.31) & -1.48 & 4.34 & \text{Discordant} \\
(3,4) & (-0.45, -2.43) & (-0.56, -5.04) & 0.11 & 2.61 & \text{Concordant} \\
(3,5) & (-0.45, -2.43) & (4.03, 3.20) & -4.48 & -5.63 & \text{Concordant} \\
(3,6) & (-0.45, -2.43) & (3.21, 2.31) & -3.66 & -4.74 & \text{Concordant} \\
(4,5) & (-0.56, -5.04) & (4.03, 3.20) & -4.59 & -8.24 & \text{Concordant} \\
(4,6) & (-0.56, -5.04) & (3.21, 2.31) & -3.77 & -7.35 & \text{Concordant} \\
(5,6) & (4.03, 3.20) & (3.21, 2.31) & 0.82 & 0.89 & \text{Concordant} \\\end{array}
\]
Step 2: Count the Pairs
Step 3: Compute Kendall’s Tau
\[
\tau = \frac{C – D}{\binom{6}{2}} = \frac{12 – 3}{15} = \frac{9}{15} = 0.6
\]
Practice Question
Suppose that we know from experience that \(\alpha\) = 3 for a particular financial variable, and we observe that the probability that X > 10 is 0.04.
Determine the probability that X is greater than 20.
A. 125%
B. 0.5%
C. 4%
D. 0.1%
The correct answer is B.
From the given probability, we can get the value of constant k as follows:
$$ \begin{align*} \text {prob}(\text X > \text x) & = \text{kx}^{(-\alpha)} \\ 0.04 & = \text k(10)^{(-3)} \\ \text k & = 40 \\ \end{align*} $$
Thus,
$$ \text P(\text X > 20) = 40(20)^{(-3)} = 0.005 \text { or } 0.5\% $$
Note: The power law provides an alternative to assuming normal distributions.