Futures Markets

After completing this reading, you should be able to:

• Define and describe the key features and specifications of a futures contract, including the underlying asset, the contract price and size, trading volume, open interest, delivery, and limits.
• Explain the convergence of futures and spot prices.
• Describe the role of an exchange in futures transactions.
• Explain the differences between a normal and inverted futures market.
• Describe the mechanics of the delivery process and contrast it with a cash settlement.
• Evaluate the impact of different trading order types.
• Describe the application of marking to market and hedge accounting for futures.
• Compare and contrast forward and futures contracts.

The Key Features of a Futures Contract

A futures contract is a standardized, exchange-tradable obligation to buy or sell a certain amount of an underlying good at a specified price on a specified date.

Key Features:

• Exchange-tradable: Unlike forwards, which trade on OTC markets, futures contracts are traded on an organized exchange with a designated physical location.
• Standardization: With respect to forward contracts, specific details about quality to be delivered, price, and delivery date are subjects of negotiation between the buyer and the seller. In futures contracts, however, the choice of expiry dates is limited, and trades have fixed sizes. This standardization paves the way for an active secondary market where trades can be executed. However, perhaps the most pronounced benefit is increased liquidity.
• Marking to market: Since the clearinghouse must monitor the credit risk between the buyer and the seller, it performs daily marking to market. This is the settlement of the gains and losses on the contract on a daily basis. It avoids the accumulation of large losses over time, which can lead to a default by one of the parties.
• Margins: Daily settlements may not provide a buffer strong enough to avoid future losses. For this reason, each party is required to post collateral that can be seized in the event of default. The initial margin must be posted when initiating the contract. Suppose the equity in the account falls below the maintenance margin. In that case, the relevant party receives a margin call- a requirement to provide additional funds to restore the margin account to the initial level.
• Clearinghouse: The clearinghouse is an interposed party between the buyer and the seller, which ensures the performance of the contract. In essence, futures contracts have no credit risk. Each exchange has a clearinghouse. The clearinghouse splits each trade and acts as the opposite side of each position. It’s the buyer to every seller and seller to every buyer. In other words, there is no direct contact between the short and long parties. It’s the clearinghouse that makes margin calls whenever the need arises. In OTC markets, clearinghouses play a similar role.
• Position limits: The number of contracts that a speculator can hold is capped at a certain value by the exchange. The aim is to prevent speculators from having an undue influence in the market.

Long exposure in a futures contract means the holder of the position is obliged to buy the underlying instrument at the contract price at expiry. The holder will make a profit if the price of the instrument goes up. Conversely, they will make a loss if the price goes down. The long futures position can be entered by a speculator who expects the price to rise.

Short exposure in a futures contract means the holder of the position is obliged to sell the underlying instrument at the contract price at expiry. The holder will make a profit if the price of the instrument goes down. Conversely, they will make a loss if the price of the underlying rises dramatically.

Open Interest

Open interest refers to the number of existing contracts at any point in time. Consistently, the number of long positions always equals the number of short positions. As such, open interest can be described as the number of net long contracts (short contracts).

 The net interest of trade is zero at the beginning of the contract. The open interest slowly rises as the trade progresses to a maximum amount seen before delivering the contract. For instance, consider a futures contract between two parties:

• When both parties take new positions, the open interest increases by one.
• When one party closes out a position while the other takes a new position, the open interest remains constant.
• When both parties close out their respective positions, the open interest decreases by one.

Specification of Contracts

Exchanges should clearly be defined as what is being traded in a futures contract. In a case where there are diverse deliverables, the location and time of delivery should be clearly defined, and the party with the short position has the right to choose. The specifications of the futures contract include:

• The contract size.
• Delivery location.
• Time of delivery.
• The underlying asset.
• The price quotes
• The price limit.
• Position limits.

Size of the contract

Exchanges should determine the size of their contracts to cater to both small (retail) and large (large corporations) scale traders. Compared to an agricultural product, the value of what is delivered for a contract on a financial asset is typically much higher.

Delivery Location

Futures contracts on commodities require the specification of the delivery location while taking into consideration the transportation costs. Note that for some contracts, transportation cost also determines the price of the futures contracts.

Time of Delivery

The time to delivery is usually specified in months. At the close of trading, the price of the futures contract is known as the settlement price. It determines the amount and the trader who gets the variation margin.

The future price can either start above or below the spot price. It, however, converges at the spot price as the period of delivery nears. If the prices do not converge and the futures price is above the spot price, traders can hedge by:

1. Shorting futures,
2. Buying spot assets, and
3. Making the delivery of the contract.

If the price is below the spot price, traders will buy the asset and make the future prices rise towards the spot price. Arbitrage opportunities such as these do not last long in the market since the investors take advantage and disappear quickly.

The Underlying Asset

Typically, futures contracts are written on financial assets such as currencies and commodities such as agricultural products. For financial assets, the definition of underlying is plain and simple. For instance, the CME Group defines the underlying asset of one contract on euros as 125,000 euros.

In the case of commodities, grading (based on quality) must be clearly specified of the commodities to be delivered. For instance, a contract should specify if the actual orange fruits or their concentrates are delivered.

Failing to specify the grading system of commodities by the exchange could cause the contract to be terminated. The trader in a short position can deliver low-quality products, which the trader in a long position can reject.

Price Limits

Price limits are set by the exchange and subject to change from time to time. Price limits within which future prices can move in either direction. These movements are known as limit movements. If the limit movements are exceeded, trading is stopped.

When a limit is reached and results in a price increase, the contract is termed the limit up. Conversely, if the limit movement results in a price decrease, the contract is called limit down.

The price limits help in preventing huge price movement due to speculation. On the downside, if the price limits result from the new information reaching the market, then the price limits obstruct the determination of the true market prices.

Position Limits

Position limit cabs the size of a position that a speculator can hold in the futures contract. Position limits are meant to prevent speculators’ domination, which can result in an unacceptable market influence. Position limits are in tens of thousands of contracts.

Delivery Mechanics

Delivery of the underlying assets rarely happens in the futures markets as traders strive to close out their positions before the contract’s maturity.

Assets can, however, be traded at spot markets using the most recent settlement price. Thus, the mechanics of delivery is crucial in futures markets.

The delivery time of a contract varies from one contract to another. The delivery process of the contract is initiated when a trader in a short position issues a notice of intention to deliver to the exchange central counterparty clearing house (CCP). The notice includes the number of contracts to be delivered and, in the case of commodity products, the grade of the commodity and location of delivery.

The exchange then chooses one or more traders with a long position to accept the contracts. Typically, traders who have had net long positions are allocated the delivery notices, but sometimes traders are allocated randomly. The members cannot deny the delivery notices and are often given a short period of time to transfer the contracts to other members.

The first notice day is the first day when the delivery notice is sent to exchange CCP. The last notice day is the last day when submission of the delivery notice to exchange CCP can be done.

The price paid for an asset is defined as the most recent settlement price and sometimes adjusted for the delivery location, grade, warehousing cost, and other factors.

Cash Settlements

Cash settlements save traders’ delivery processes and costs. However, regulators try to discourage cash settlements since they resemble a gambling process. Therefore, delivery of physical settlements is preferred when it is possible.

However, CME Group’s futures contracts on the S&P 500 are settled in cash. Other contracts settled in cash are contracts that depend on weather and real estate prices.

Market Participants

The futures market participants include:

• Futures Commission Merchants and Introducing Brokers: They trade on behalf of their clients. Futures Commission merchants also manage clients’ funds.
• Locals: Traders who trade on their own. Locals and the clients of the futures commission merchants can be classified as:
  • Scalpels: They close out future positions within a very short time.
  • Day traders: They close out trading positions on the same day they took the position.
  • Position Traders: They take positions that reflect market movements over time.

The Convergence of Futures and Spot Prices

The spot price is the current market price at which an instrument or commodity is bought or sold for immediate payment and delivery. On the other hand, the futures price is the price of an instrument/commodity today for delivery at some point in the future, called the maturity date. The difference between the two is called the basis.

$$ \text{Basis}=\text{Spot Price – Futures Price} $$

As the maturity date nears, the basis converges toward zero,  i.e.,  the spot price tends towards the futures price. The two rates must be equal as long as no arbitrage opportunities exist on the actual maturity date. At maturity, the futures price becomes the current market price, which is actually the definition of the spot price.

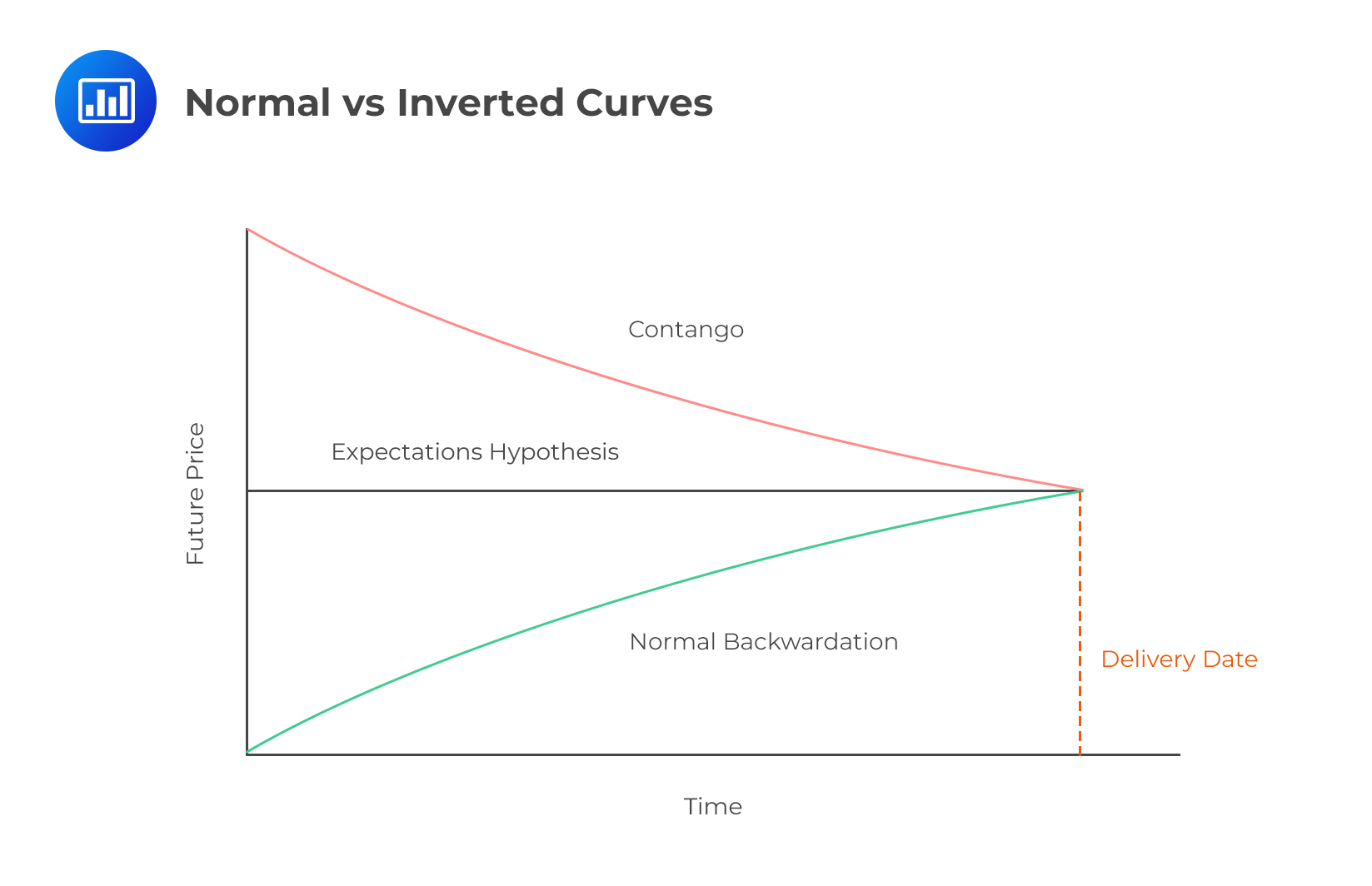
Normal and Inverted Futures Markets

A normal futures market, also known as a Contango market, means that futures contracts are trading at a premium to the spot price. For example, suppose the price of a barrel of crude oil today is $50 per barrel, but the price for delivery in three months is $53: the market would be in Contango. On the other hand, if crude oil is trading at $50 per barrel for delivery right now, and the three-month contract is trading at $45 per barrel, then that market would be said to be inverted (backwardation).

A normal futures curve will show a rising slope as the prices of futures contracts rise over time. An inverted futures curve will show a falling slope as the prices of futures contracts fall over time.

Terminating a Futures Contract

Traders with short or long positions in futures contracts can terminate them in one of four ways:

• Delivery: A short terminates the position by delivering the goods, and the long pays the contract price. This is called delivery. In each exchange, certain conditions must be met before delivery can be executed. Such conditions are contained in the “intention to deliver” file. This method is, however, hardly used.
• Closeout: This is a scenario where the futures trader closes out the contract even before the expiry. If a trader has a long position, they will take an equivalent short-term position in the same contract, and both positions will offset each other. Similarly, if a trader has a short position, they will take an equivalent long-term position in the same contract, and both positions will offset each other.
• Cash settlement: In this scenario, a trader leaves his position open, and when the contract expires, his margin account will be marked-to-market for P&L on the final day of the contract.
  Exchange-for-physicals: In this case, a trader finds another trader who has an opposite position in the same futures contract and delivers the underlying assets to them. This happens outside the designated trading floor, but the traders are obliged to inform the clearinghouse of the transaction immediately afterward.

Placing Orders

A trader uses a futures order or options order to tell his broker exactly what to buy or sell when to do it, and at what price. There are several order types:

• Market order: A market order is executed at the best possible price. A market order instructs the executing broker to buy or sell futures contracts immediately at the market price, the best possible price.
• Limit order: Limit orders are orders where the trader specifies the price limit. As such, limited orders can only be carried out at a specified price or at an attractive price to the trader. A limit buy order is placed below the current market price, while a limit sell order is placed above the current market price.
• Stop-loss order: Limits a trader’s loss by making the order a market order once the asset reaches a less favorable price.
• Stop limit order: It’s an order that specifies both the stop and the limit price. If the spot price is attained, the order will be called a limit order. If the spot price equals the limit price, the order will be called a spot and limit order.
• Market if touched order/Board order: Traders trade at a specified or at a more favorable price. In other words, market if touched orders become market orders if a trade is executed at a specified price or more attractive price.
• Discretionary/Market not held order: Trader delays the order with the hopes of finding better prices for the asset.

Duration of Orders

Orders are to be executed by the end of the day, failure to which leads to cancellation. Traders specify other periods of time when the trade is active. A fill-or-kill order is an order that is canceled if not executed within a few seconds. An open order or good-till-canceled order is an order that is only canceled upon a trader’s request; otherwise, the order remains open for the remaining life of the futures contract.

Regulation of Futures Markets

Regulations vary from country to country. The work of these regulators include:

• Ensuring that future markets remain open, giving out licenses to traders.
• Ensuring that the markets operate transparently.
• Ensuring that the markets are financially okay.
• Handling complaints arising from market participants.
• Overseeing the setting up of position limits.

Accounting

Gains and losses from futures markets are accounted for as they occur, a valuation process called marking to market. Consider the following example:

Consider an oil company with the fiscal year ending December. The company sells 1000 two-year futures contracts at the end of May when the futures price is $65 per barrel of crude oil. Each contract consists of selling 1,000 barrels of crude oil. Over the period of two years, the  following happened:

• The future price of crude oil was $62.5 in the December of the first calendar year.
• The futures price decreases to $61 per barrel in the December of the second year.
• The contract is close out at $64.5 per barrel at the end of May of the third year.

The profit to the oil company is calculated as follows:

First year: (65-62.5)× 1,000 × 1,000 = $250,000

Second year: (62.5-61)× 1,000 × 1,000 = $150,000

Third year: (61-64.5)× 1,000 × 1,000 = -$350,000

 Typically, futures are settled daily so that the cash in line with profits earned in the years is accounted for.

Hedging Accounting for Futures

Accounting for the profits and losses when hedging using futures contracts can lead to high earning volatility, which goes against the notion of hedging. Thus, if a company hedges against its position, it must take into consideration the hedging accounting.

The hedging accounting allows the profits (or losses) from the hedging strategy to be recognized simultaneously as the loss (or profits) on the hedged items.

Examples of regulations are: the Financial Accounting Standard Board (FASB) has provided statements FAS 133 and ASC 815, which explains when hedge accounting can and cannot be used by US companies. On the same note, the International Accounting Standards Board (IASB) has given out IAS 39 and IFRS 9.

If we consider the oil company example above and assume that it qualifies for hedge accounting, the gain of $500,000 [=(65-64.5)× 1,000 × 1,000 ] will be accounted for in the third year.

The rules governing hedging accounting are strict in that the hedge must be entirely documented (for example, with regard to items being hedged and hedging instruments). Moreover, the hedge must be classified as effective, implying that and economic activity that is not affected by credit risk must link the hedging instrument and the hedged instrument. Moreover, the efficacy of the hedge must be tested regularly.

Comparison between Futures and Forwards

Similarities

They both are an agreement to trade an item at a later date at a pre-determined price.

Differences

$$ \begin{array}{l|l} \textbf{Futures} & \textbf{Forwards} \\ \hline \text{Traded on an exchange.} & \begin{array}{l} \text{Traded in an OTC market and} \\ \text{are thus more prone to credit} \\ \text{risk.} \end{array} \\ \hline \begin{array}{l} \text{Both financial and non-financial} \\ \text{variables can be traded.} \end{array} & \begin{array}{l} \text{Mainly traded on interest rates} \\ \text{and foreign exchange.} \end{array} \\ \hline \begin{array}{l} \text{Trades are settled on a daily} \\ \text{basis.} \end{array} & \begin{array}{l} \text{Trades are settled at the end of} \\ \text{the life of the asset.} \end{array} \\ \hline \begin{array}{l} \text{Delivery is rare as traders close} \\ \text{out positions before the} \\ \text{delivery date.} \end{array} & \text{Actual delivery is made.} \\ \hline \text{The delivery date is specified.} & \begin{array}{l} \text{The delivery period is specified} \\ \text{and can be a whole month.} \end{array} \\ \end{array} $$

Question

A trader wishes to sell different grades of corn. Which of the below statements best describes how the price of the corn should be quoted?

A. Quote prices would be the same price for all corn

B. Quote prices would be different prices for each harvest period

C. The exchange would randomly decide which grade would be a higher/lower price

D. Quote prices would correspond to the quality of the corn

The correct answer is D.

Different prices should be quoted for each of the grades available. The prices should further correspond to the quality of the corn. The highest grade should be priced more than the lowest grade.

A is incorrect: The same price should not be quoted for all corn. This is because the price will not be a true reflection of the value of the corn.

B is not the BEST answer: The prices should not only be different but also reflect the grade of the corn.

C is incorrect: Randomly deciding on the price of the corn may lead to overpricing low-quality corn and underpricing high-quality corn.