Future Value and Exposure
After completing this reading you should be able to: Describe and calculate the... Read More
After completing this reading, you should be able to:
Counterparty risk is the risk that one or more parties in a financial transaction will fail to fulfill their side of the contractual agreement. It may arise either as a result of the counterparty’s unwillingness to observe the contractual obligations or a default, possibly occasioned by poor financial health.
Counterparty risk generally emerges in two main types of financial contracts namely:
Lending risk, also known as credit risk, is the risk that a borrower will fail to pay the principal, interest, or some of it due to insolvency. As a result, the creditor may suffer cash flow disruptions and increased collection or recovery costs.
$$ \begin{array}{c|c} \textbf{Lending risk} & \textbf{Counterparty risk} \\ \hline {\text{The notional amount at risk is known at } \\ \text{any time during the life of the contract } \\ \text{with some degree of certainty. When } \\ \text{buying a bond, for example, the notional } \\ \text{amount at risk is close to par. Variables } \\ \text{such a s a floating rate of interest only } \\ \text{create moderate uncertainty over the } \\ \text{amount owed}} & {\text{The value of the contract in the future is } \\ \text{uncertain. The MTM value of a } \\ \text{derivative at any date is the net of all } \\ \text{future cash flows that are highly } \\ \text{uncertain}} \\ \hline {\text{Only one party has lending risk – the } \\ \text{creditor}} & {\text{Risk is bilateral – each party in the } \\ \text{derivative transaction has a risk to the } \\ \text{other. The contract value can be positive } \\ \text{or negative}} \\ \end{array} $$
Before looking at some of the transactions that carry counterparty risk, it is important to mention that counterparty risk takes two forms: pre-settlement risk and settlement risk.
Pre-settlement risk is the risk that a counterparty will default prior to the expiration date of the contract, i.e., prior to the final settlement of the transaction.
Settlement risk is the counterparty risk during the settlement process. It arises because the parties to a transaction, such as a forward contract, do not execute or rather perform their obligations at the agreed time. For example, there may be a delay in the delivery of collateral or instrument underlying a contract.
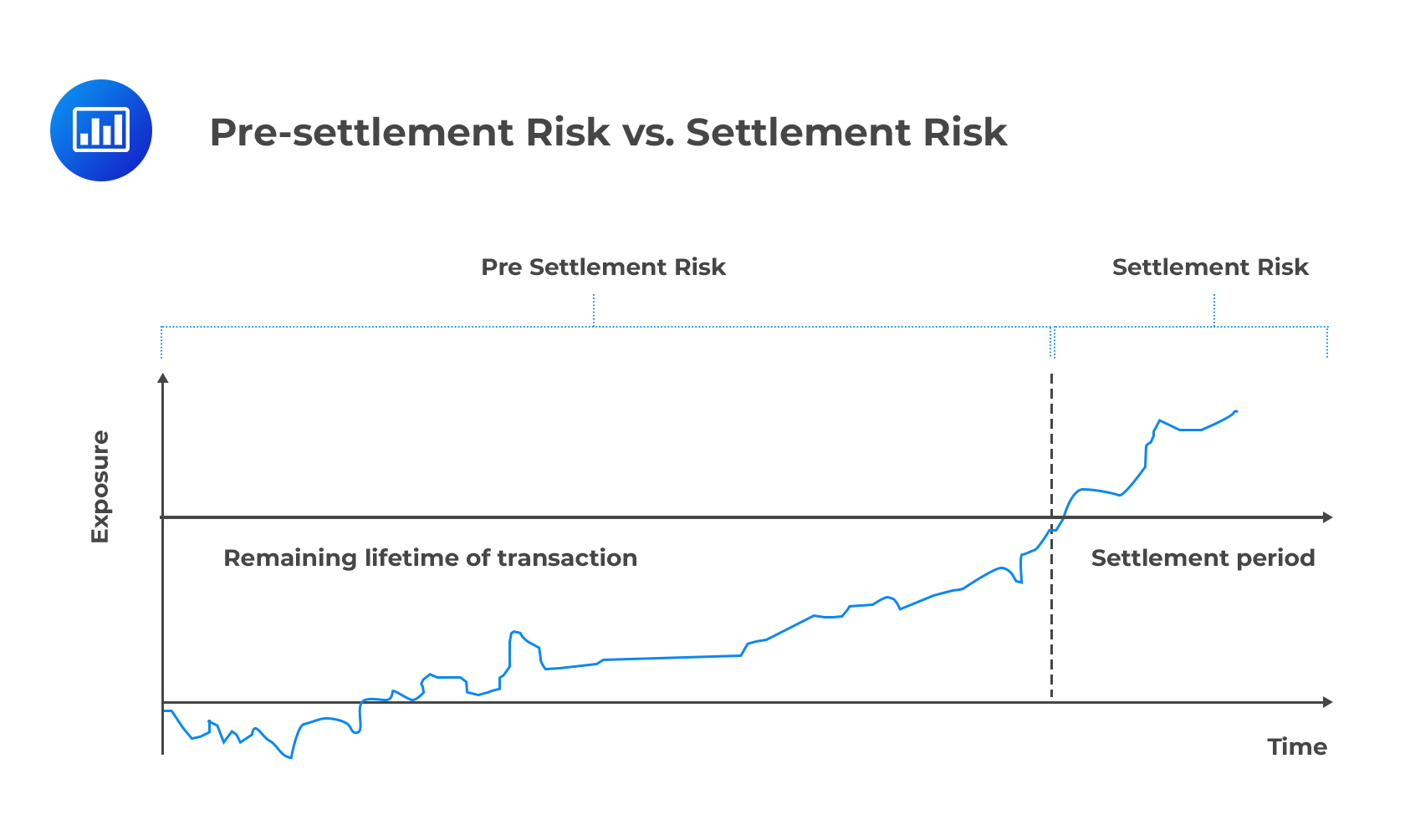 Transactions that occur through an exchange (such as the New York Stock Exchange, NYSE, or the Tokyo Stock Exchange, TSE) are generally considered to be free of counterparty risk because the exchange itself is the counterparty to every participant. In this reading, therefore, we are going to look at counterparty risk in terms of securities financing transactions and OTC derivatives.
Transactions that occur through an exchange (such as the New York Stock Exchange, NYSE, or the Tokyo Stock Exchange, TSE) are generally considered to be free of counterparty risk because the exchange itself is the counterparty to every participant. In this reading, therefore, we are going to look at counterparty risk in terms of securities financing transactions and OTC derivatives.
In simple terms, securities financing transaction (SFT) is any transaction that allows a party to use its assets, such as stocks or bonds, to secure funding for its activities. SFTs encompass the following:
A repurchase agreement (or simply “repo”) involves the sale of a security in an arrangement where the seller will buy back the same security from the same buyer at an agreed-upon price. The lender receives the repo rate which combines a risk-free rate and a risk premium. Collateral is provided in the form of liquid marketable securities. When a repurchase agreement is viewed from the perspective of the cash lending party, it is commonly called a reverse repurchase agreement.
Each market participant in a repurchase agreement is exposed to counterparty defaults, regardless of the collaterals posted. The agreement is such that the lender of funds is always the most vulnerable party. The seller may fail to repurchase the security at maturity as promised. If that happens, the lender would have to liquidate the collateral provided to recover the cash loaned out.
However, it is difficult to liquidate collateral at its market value, more so in stressed market conditions. Therefore, a repo margin (called haircut in the US) is imposed. It is the difference between the market value of the security used as collateral and the value of the loan. For example, let’s assume that a 3% haircut applies, and a seller wishes to be funded to the tune of $100 million. In this case, the seller would have to provide collateral with a market value of $103.0928 million [=$100m/(1-0.03)] in order to receive the $100m loan.
In essence, therefore, the haircut protects the buyer or lender against:
As noted earlier, counterparty risk is common in OTC derivatives such as foreign exchange forwards, interest rate swaps, and credit default swaps.
In a foreign exchange forward, two parties lock in the exchange rate for a given pair of currencies on a future date. For example, an institution may enter a contract to exchange $2m for €1.8m at a specified date in the future (note that this implies an exchange rate of €0.9 per dollar). In this case, the institution bears settlement risk in that it could pay out $2m but fail to receive €1.8. However, this occurs on the designated maturity date or expiration of the contract.
The institution also bears the pre-settlement risk. This, however, is just equal to the difference in market value between the dollar and the Euro payments, and it could materialize anytime during the life of the contract.
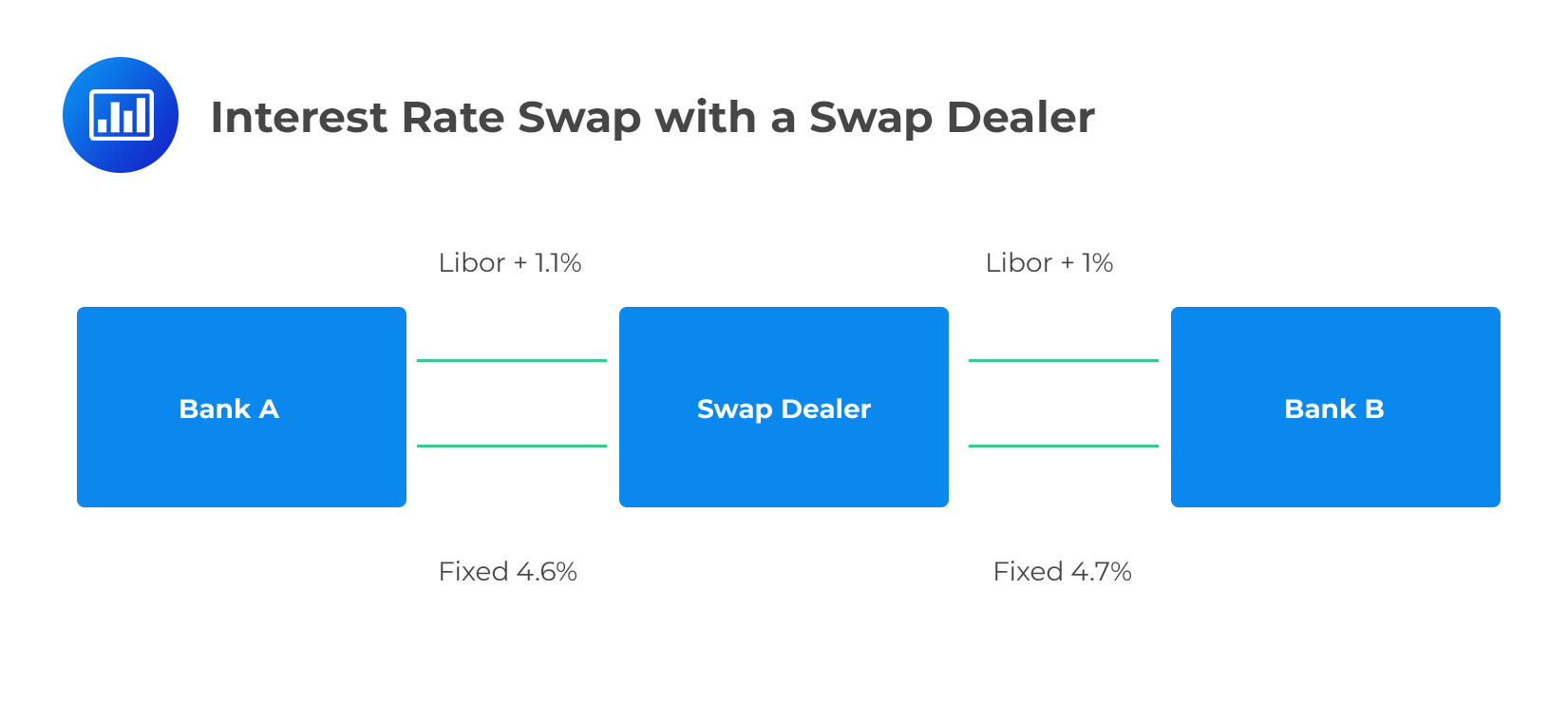
Interest rate swaps carry some counterparty risk because the other party may fail to make floating/fixed cash payments as and when required. However, counterparty risk is reduced because there is no exchange of principal. This risk is further reduced through netting, where only the difference between the floating payment and the fixed payment is exchanged periodically.
 Credit Default Swaps——fault swaps do have counterparty risk in the form of wrong-way risk.
Credit Default Swaps——fault swaps do have counterparty risk in the form of wrong-way risk.
A wrong-way risk occurs when a decrease in the counterparty’s credit quality coincides with an increase in exposure. According to the International Swaps and Derivatives Association (ISDA), wrong-way risk occurs when “exposure to a counterparty is adversely correlated with the credit quality of that counterparty.” For example, let’s say party A has invested in Lebanese sovereign debt but has bought CDS protection from a Lebanese bank. If the Lebanese debt suffers a rating downgrade, party A will appear to be “winning” because if the Lebanese government defaults, it will be compensated by the bank. However, the ability of the bank to meet its obligations will likely be hurt as a result of the credit rating decline.
Institutions that take on significant counterparty risk can be split into three classes:
These are typically large banks that have high numbers of derivatives on their books. They often trade with each other but also have a large number of clients coming from other sectors within the finance industry. These banks participate in just about every derivative product available on the market, including interest rate swaps, foreign exchange forwards, and credit derivatives. Players in this category almost always post collateral against their positions
These are typically smaller banks, hedge funds, and pension funds. Players in this category trade with a relatively large number of clients. They are active in a large derivatives market. Also, they may not always post collateral against positions.
These can be small financial institutions, large corporates, or sovereign entities with significant derivatives requirements. For example, they may be looking to hedge their investments. They have just a few derivatives trades on their books and have a relatively small number of counterparties. They may also specialize in a certain asset class, say, foreign exchange products, and often do not post collateral.
In general, large derivatives players have the highest credit quality. Prior to the 2007/2008 financial crisis, for example, their credit spreads amounted to just a few basis points per annum. However, small players, such as insurance firms and pension plans, have over the years demonstrated strong credit quality and even managed to bargain for favorable trade terms such as one-way collateral agreements.
Be that as it may, the credit quality of large players should never be ignored. Events over the last couple of years have only reinforced the idea that the bilateral nature of risk is ever-present.
In a transaction, credit exposure refers to the loss suffered in the event that a counterparty defaults. For example, assume that party A and party B are engaged in a contract and at some point after inception (but before maturity), party A has a positive value Y (it’s owed money) while party B has a negative value, -Y(i.e., it owes money). In this case, the credit exposure of party A “conditional” on party B is Y; this is the amount A will lose if B defaults.
Note that if party B defaults when party A has a negative value, the latter cannot just walk away. In other words, a default by the counterparty even when you’re “losing” doesn’t somehow make you liability-free. You will still be expected to settle the amount you owe.
Credit exposure is a particularly time-sensitive measure because default can happen at any time. In some cases, default occurs years into the future and we must, therefore, consider the impact of such an event. To map out the credit exposure at a particular time, we must ask ourselves two key questions:
It is important to note that for derivative contracts where there’s no exchange of principal at the onset, the creditor is only at risk for the replacement cost, not the full amount of the trade. Also important is the fact that all exposure calculations assume that there’s a zero recovery rate in the event of default. The exposure is, therefore, the loss, as defined by the value or replacement cost that would be incurred, assuming no recovery.
Credit migration refers to discrete changes in credit quality as indicated by a rating downgrade or upgrade. For example, if a bank, initially rated AAA is downgraded to AA, the bank is said to have undergone a rating migration. What this means is that the bank has moved from one class of risk to another.
In the context of derivative contracts, we are particularly concerned with negative rating migrations, i.e. a deterioration in the credit quality of the counterparty over the term of the contract. In some cases, the time horizon can extend to several years into the future.
Credit migrations are important because they influence the term structure of default probability. In this regard, we make three observations:
One of the observations supported by strong empirical evidence strongly suggests that credit quality exhibits mean reversion. This means that the rating of institutions with good credit quality tends to decline over time. The rating of institutions with poor credit quality, on the other hand, tends to improve. What does this imply for counterparties? If a counterparty has a good credit quality at present, they are unlikely to default in the short term but their probability of default will tend to increase over time. If the credit quality is poor as of today, the counterparty will be more likely to default in the short term than in the longer term.
The recovery rate represents the percentage of the outstanding claim that is likely to be recovered following an event of default. Closely related is the loss given default which is the percentage actually lost in the event of default. The loss given default is 100% minus the recovery rate in mathematical terms. If the recovery rate is 40%, for example, then the loss given default s 60%.
Since default claims can vary significantly, LGD is highly uncertain. And while the LGD in the context of derivatives very closely matches the LGD in the debt market, there’s a small difference. When a bond issuer defaults, the LGD can quickly be determined by selling the bond in the market. However, when it comes to OTC derivatives, the LGD cannot be determined immediately because OTC derivatives are quite illiquid and cannot be traded or sold, especially when the counterparty to the derivative is in default.
Mark-to-market (MTM) is the present value of all the payments that a party is expecting to receive, less those it is obliged to make. These payments may be scheduled to occur over a long period and show a strong dependence on market variables. As such, the current MTM does not constitute an immediate liability by one party to the other. Contracts are marked to market to show the current market value of the contract with respect to each counterparty. MTM can be positive or negative depending on the magnitude of all future payments and current market rates.
Since the MTM with respect to a particular counterparty defines the net value of all positions, it is directly related to what could potentially be lost today in the event of a default. However, the MTM doesn’t always equal the amount that could possibly be in the presence of netting and provision of collateral.
Replacement cost refers to the entry cost into an equivalent transaction(s) with another counterparty. Although the MTM is an indicator of replacement cost, the two are not always equal when we factor in transaction costs and bid-ask spreads.
There are several methods that can be used to manage counterparty risk:
Cross-product netting, often known simply as netting, refers to a process in which cash flows are offset and combined into a single net amount. Netting occurs when a set of bilateral contracts have both positive and negative values.
Following a default event, a counterparty cannot demand payments on positive value contracts while stopping payments on negative value contracts. Netting reduces the exposure to the net value for all the contracts covered by the netting agreement. It is an effective way of preventing “cherry-picking” by the administrator of the defaulted counterparty.
However, netting comes with legal risk because, in some jurisdictions, the practice may not be anchored in law and, therefore, cannot be enforced. Netting also increases the exposure of other creditors (other parties with positive claims against a counterparty).
Below is an example that illustrates how netting works (from the perspective of a bank).
$$ \textbf{An Illustration of Cross Product Netting} $$
$$ \begin{array}{c|c|c} \text{} & \textbf{Bank} & \textbf{Counterparty} \\ \hline \text{Trades with +ve MTM } & {+$20} \text{ million} & {-$20} \text{ million} \\ \hline \text{Trades with -ve MTM } & {-$15} \text{ million} & {+$15} \text{ million} \\ \hline \text{Exposure in the absence of netting} & {+$20} \text{ million} & {+$15} \text{ million} \\ \hline \text{Exposure with netting} & {+$5} \text{ million} & {$0} \\ \end{array} $$
Collateralization is a contractual obligation for counterparties to post securities or cash against MTM losses. For example, the netted exposure for a bank in our example above is large and positive. This means that the bank stands to lose quite a lot in the event that the counterparty defaults. A collateral agreement would reduce this exposure by requiring the counterparty to post collateral to the bank to support the exposure. In most cases, however, collateral is two-way, meaning that either counterparty is required to post collateral against a negative MTM.
Collateralization is associated with three types of risk:
Like netting, however, collateralization increases the exposure of other creditors in a default scenario.
Close-out is the immediate cancellation of all contracts with the counterparty that has defaulted. At the point of default, all the remaining contractual obligations are terminated, and the final positive or negative positions are combined into a single net payable or receivable. The result is an immediate realization of net gains or losses.
There are more ways counterparties can use to manage counterparty risk:
Counterparties can also hedge against default events and their exposures with a range of instruments, especially credit derivatives such as credit default swaps. Hedging, however, creates operational risk and market risk through mark-to-market volatility of hedging instruments.
Central counterparties, also known as CCPs, protect market participants from counterparty risk by guaranteeing the trade between a buyer and a seller. The CCP themselves aim to be financially sound by demanding collateral and other financial obligations from their members. By doing so, the CCPs help avert the cascading impact a counterparty default could have on the financial markets as was seen in 2008 in the wake of the collapse of Bear Stearns.
CCPs in essence help to centralize counterparty risk by acting as intermediaries between market participants. By so doing, they create liquidity risk and systemic risk because the failure of CCP can trigger significant system-wide disturbance.
Hedging, collateralization, and netting are also possible ways of mitigating counterparty risk.
Methods used to mitigate or manage risks are not 100% effective. They cannot eradicate risk completely. It is therefore important for an institution to correctly quantify the remaining counterparty risk and ensure that compensation is commensurate with the level of risk.
In general, there are three levels at which counterparty risk can be quantified:
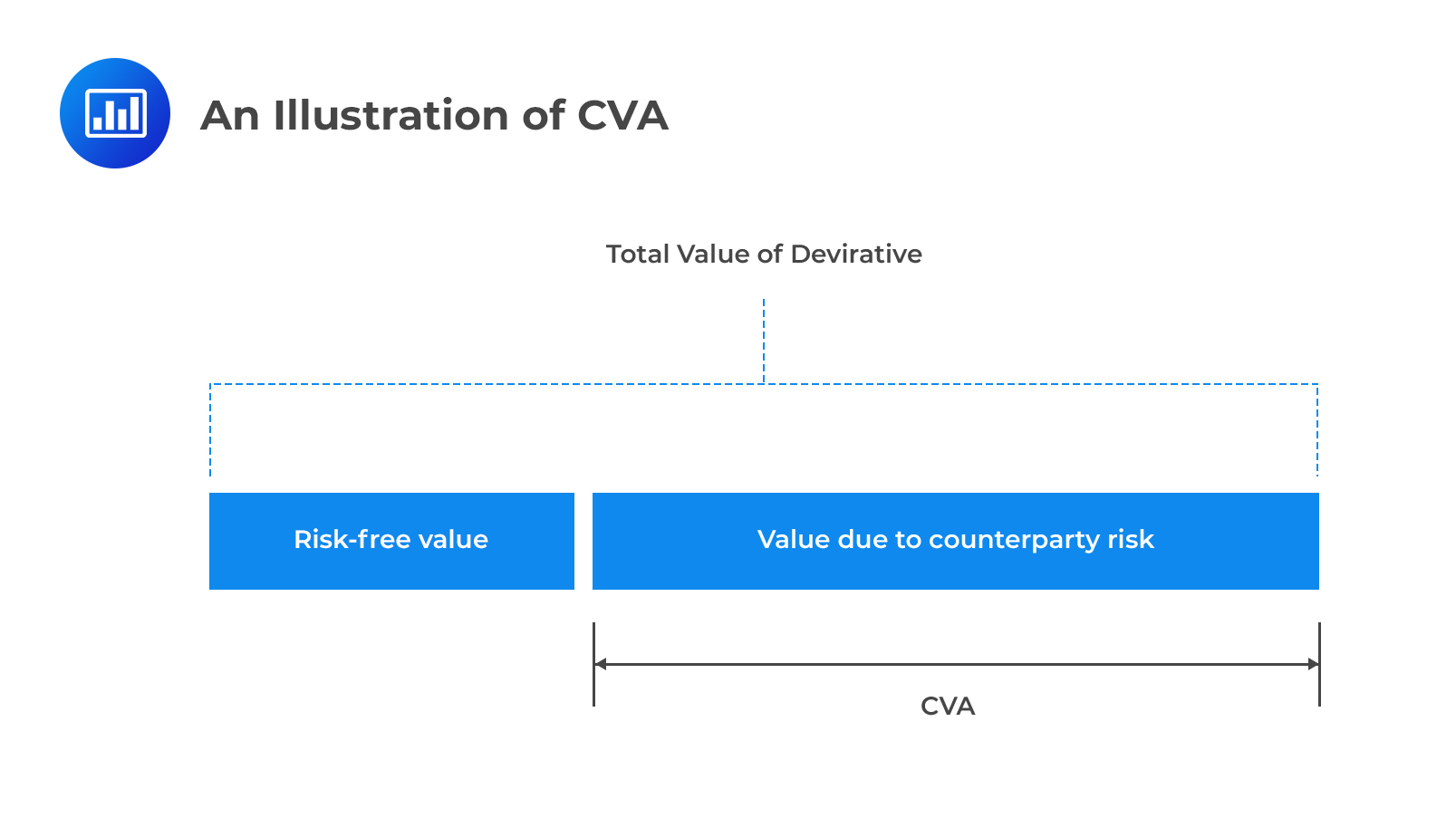
When valuing derivatives, we can generally split up the process into two portions:
The adjustment that takes the counterparty risk into account is known as the credit value adjustment (CVA). In other words, CVA represents the market value of the counterparty credit risk. The objective of traders is to earn a return that’s greater than CVA.
 Credit limits are the techniques used to put a cap on the amount of counterparty risk taken. Credit limits and CVA complement each other and are popular methods of managing counterparty risk. However, there are two main differences:
Credit limits are the techniques used to put a cap on the amount of counterparty risk taken. Credit limits and CVA complement each other and are popular methods of managing counterparty risk. However, there are two main differences:
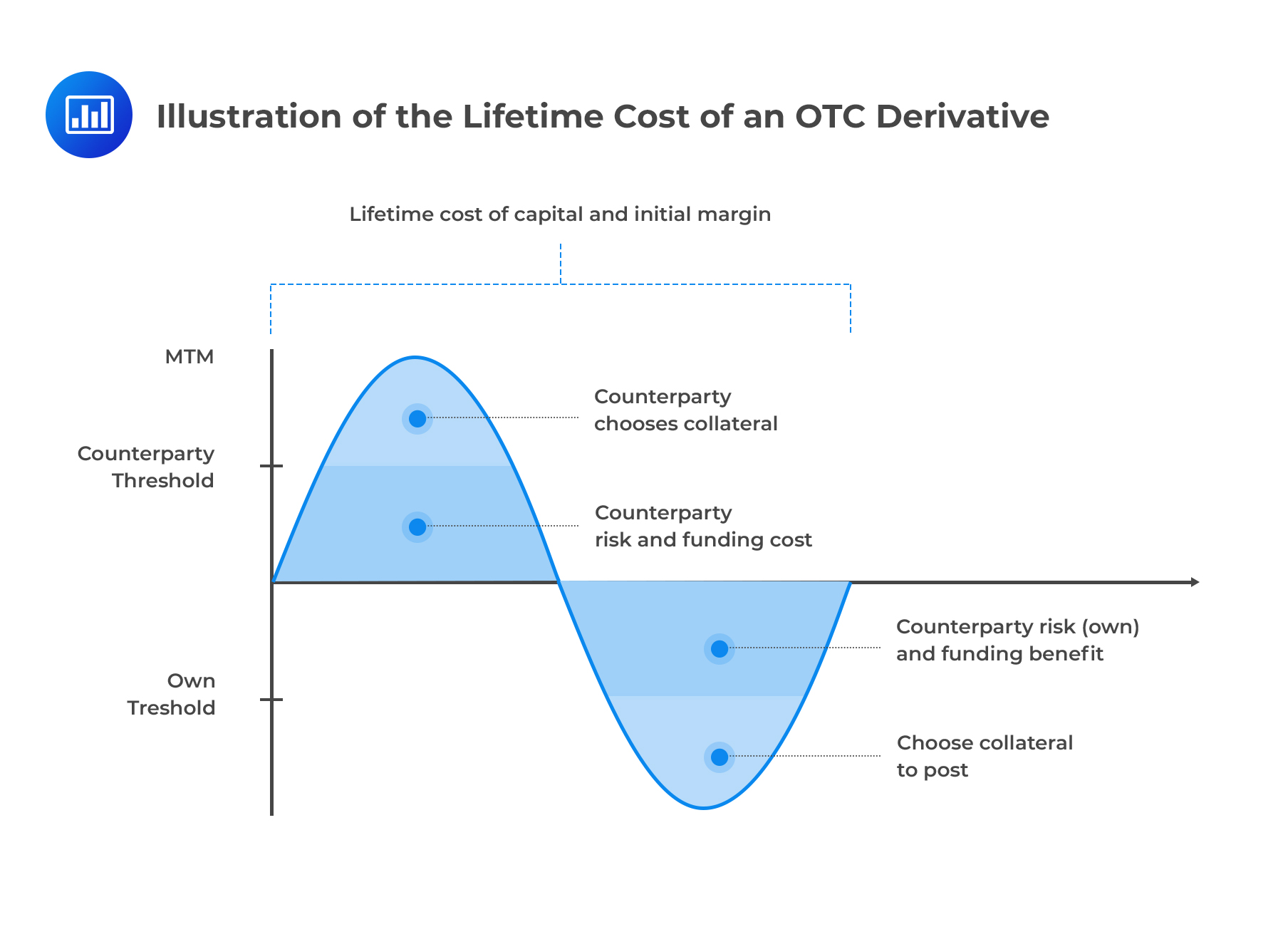
The cost of an OTC derivative is influenced by its moneyness from the point of view of a particular counterparty.
When the exposure is positive, the uncollateralized component gives rise to counterparty risk and funding costs. If a bit of or the entire MTM is collateralized, then the counterparty is at liberty to choose the type of collateral to post from a range of possible choices as specified in the contract.
When exposure is negative, there is counterparty risk from the party’s own default. The negative MTM is actually a funding benefit to the extent that they are not required to post collateral. If collateral is posted, then, the party is at liberty to choose the type to post.
Moneyness of the transaction notwithstanding, an OTC almost always comes with extra costs:
 xVA Terms
xVA TermsxVA (X-Value Adjustment) refers to the different types of valuation adjustments relating to derivative contracts. In other words, it is the general name for adjustments that are made to the fair value of a derivatives contract as a way of recognizing the presence of funding costs, counterparty risk, and regulatory capital costs.
Some of the components of xVA include the following:
CVA reflects the cost of hedging a client’s counterparty credit risk over the life of the trade. It is the difference between the risk-free portfolio and the true portfolio value.
DVA represents counterparty risk from the point of view of a party’s own default./p>
FDA is an adjustment to the value of a derivative (or a portfolio of derivatives) designed to ensure that a dealer recovers their average funding costs incurred in the process of trading and hedging derivatives.
MVA represents the cost of posting initial margin over the lifetime of the transaction.
ColVA refers to the costs and benefits associated with embedded optionality in the collateral agreement (for example, the ability to choose the type of collateral to post), and any other non-standard collateral terms.
KVA is the cost of holding capital over the duration of a transaction.
Question
A global hedge fund specializes in exotic options with only a select few counterparties in the market. As they navigate the complexities of these trades, they recognize the increasing counterparty exposure they face due to the nature of their trades and the limited players involved. The management aims to almost entirely neutralize this counterparty exposure. Which of the following strategies, if adopted, would be most effective in achieving this?
A. Require all counterparties to post a combination of cash and high-grade government bonds as collateral.
B. Engage with a wider variety of counterparties to ensure greater diversification in the trades.
C. Implement bilateral netting agreements with individual counterparties across all exotic option contracts.
D. Take out credit insurance policies against potential counterparty defaults.
Solution
The correct answer is A.
The most direct way to mitigate counterparty exposure is to hold high-quality collateral, such as cash or short-term investment-grade government bonds, against the exposure. If any counterparty defaults, the hedge fund, having an open contract with that counterparty, would be able to claim the collateral. This method provides a near-complete safeguard against the risk from potential defaults by counterparties.
B is incorrect as merely diversifying counterparties can spread the risk but not necessarily reduce it. In markets with few players, even diversifying doesn’t guarantee significantly reduced exposure. This approach may still leave substantial exposure if several dominant players default simultaneously.
C is incorrect because while bilateral netting agreements allow firms to reduce net exposure to individual counterparties by offsetting debits and credits across transactions, they don’t minimize the total counterparty exposure to almost zero, particularly when only a few significant players dominate the market.
D is incorrect as while credit insurance policies can offer some protection against counterparty defaults, they introduce another layer of risk. The insurer might default, or there could be disputes over claims, making this approach less than ideal for almost entirely neutralizing counterparty exposure.
Things to Remember
- Counterparty risk is not just about potential default but also encompasses credit risk, delivery risk, and potential replacement costs.
- High-quality collateral can be quickly liquidated, providing a cushion during times of financial distress or market turmoil.
- Legal jurisdictions can influence the effectiveness of netting agreements, making it essential to understand regional differences and enforceability.
- Operational processes, like regular collateral valuations and timely margin calls, can amplify the efficacy of risk mitigation strategies.
- Establishing clear communication channels with counterparties can foster transparency and faster issue resolution in complex trades.