Market Efficiency and Behavioral Finance
After completing this reading, you should be able to: Explain the three forms... Read More
After completing this reading, you should be able to:
- Explain the concept of no-arbitrage and the risk-neutral approach to valuing derivative securities
- Understand the concept of no-arbitrage when comparing actual and synthetic calls or when comparing actual and synthetic puts.
- Understand the concepts underlying the risk-neutral approach to valuing derivative securities in the context of the Binomial Option Pricing Model.
- Use the Binomial Option Pricing Model to calculate the value of European and American call and put options, along with the value of Asian and barrier options.
- Price options under a one-period binomial model on a stock with no dividends.
- Extend the binomial model to multi-period settings for pricing both European and American call and put options.
- Extend the binomial model to other underlying assets, including stock indices with continuous dividends, currencies, and futures contracts.
Arbitrage describes a situation where an investor can make a risk-free trading profit. In a given market, an arbitrage opportunity exists if:
In other words, arbitrage is exploiting a price imbalance in the same asset between two or more markets. For derivatives, this is taking advantage of the differences in prices of a unique asset to make a risk-free profit.
If such an opportunity exists, an investor will seek to multiply his portfolios to make an unlimited profit. However, this is mostly impossible since other active participants of the market would do the same. Thus, the prices in the market will change accordingly to eliminate the arbitrage opportunity.
For example, consider Company ABC’s stock, which trades on the New York Stock Exchange for $10.00, and the equivalent of $11.00 on the London Stock Exchange. This sets up a perfect, risk-free arbitrage opportunity. The arbitrageur can buy ABC’s stock on the New York Stock Exchange for $10.00 and simultaneously short-sell the stock on the London Stock Exchange for $11.00, making a $1 per share ‘riskless’ profit. This action by market participants would force the two prices to converge back to one price.
This principle states that arbitrage opportunities do not exist in the market. This will imply that if any combination of assets generates the same payments, they must have the same price. This is referred to as the Law of One Price.
An actual call option gives the right but not obligation to buy a given underlying asset for a specified price at maturity. On the other hand, a synthetic call, also known as a protective put, is a strategy where an investor who holds the underlying assets/security uses an in-the-money put option to mimic the performance of a call option.
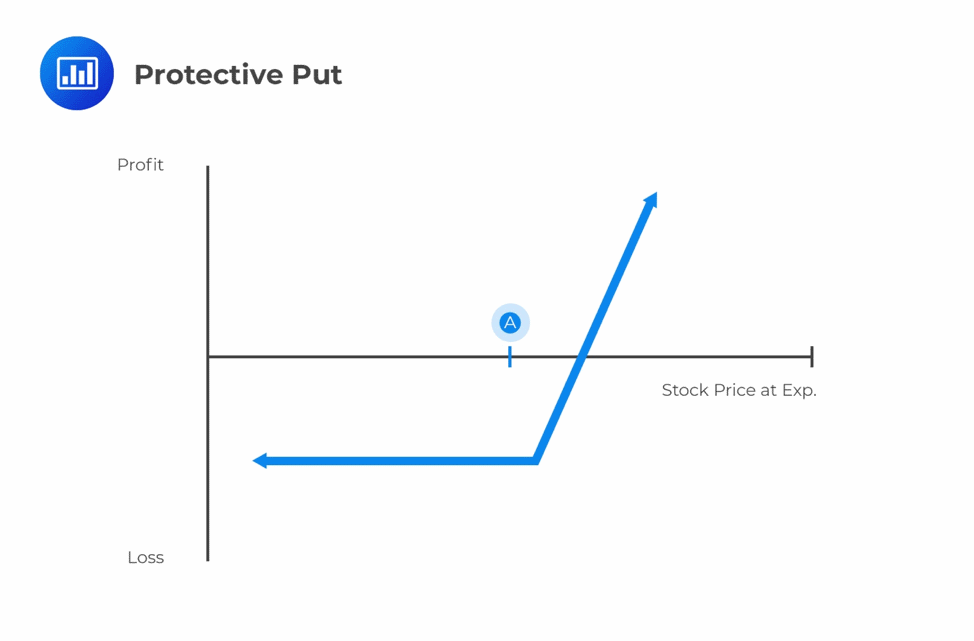
If the no-arbitrage assumption holds, we can compare an actual call and a synthetic call.
Consider the following two portfolios:
Portfolio A:
Portfolio B:
Let \(S_T\) be the underlying security price at time \(T\). At time T, the payoff from portfolio A will be:
The combined payoff is thus:
$$\max\left(0,S_T-K\right)$$
The payoff from portfolio B will be either 0 if \(S_T < K\) or \(S_T-K\) if \(S_T > K\) which can be expressed as below:
$$\max(0,S_T-K)$$
We observe that portfolios A and B are identical, and according to the law of one price, they should both have the same price.
According to the no-arbitrage assumption, the cost of setting up portfolio A should be equal to the price of portfolio B, the call option. Portfolio A is a synthetic call because it mimics the payoff from a call option by borrowing to buy shares.
The synthetic call allows the investor to benefit from an anticipated rise in the underlying price while capping his/her maximum loss to the premium paid to purchase the put.
An actual put option gives the right but not obligation to sell a given underlying asset for a specified price at maturity.
A synthetic put, also known as a protective call, on the other hand, is a strategy where an investor who is short on the underlying assets/security uses an in-the-money call option to mimic the performance of a put option.
If the no-arbitrage assumption holds, then we can compare an actual call and a synthetic call as follows:
Portfolio A:
Portfolio B:
Let \(S_T\) be the price of the underlying security at time \(T\).
At time \(T\), the payout from portfolio A will be:
The combined payoff from the investor will thus be:
$$\max\left(0,K-S_T\right)$$
The payout from portfolio B at time \(T\) will either be 0 if \(S_T > K\) or \(K-S_T\) if \(S_T < K\). This can be expressed as:
$$\max\left(0,K-S_T\right)$$
We observe that portfolios A and B are identical, and according to the law of one price, they should both have the same price.
According to the no-arbitrage assumption, the cost of setting up portfolio A should equal the price of portfolio B, the put option. Portfolio A is a synthetic put because it mimics the payoff from a put option by starting with a short stock position and a long call.
The synthetic put allows the investor to benefit from an anticipated decline in the underlying price while capping his/her maximum loss to the premium paid to purchase the call.
In the previous section, we looked at the comparison between actual and synthetic calls and puts and the application of the no-arbitrage assumption.
Replication is a term used to describe a position created by having a portfolio or combination of securities that have the same payoff with an option.
In our case, the synthetic calls and puts (Portfolio A’s) can be termed as replicating portfolios for the actual call and put options described. The investor’s interest is to determine exactly how much should amount \(Ke^{-rT}\) be borrowed or invested at time 0 and how many units of the underlying security should be held to create a replicating portfolio.
This leads us to the simplistic case below.
Suppose at time \(t = 0\), the share price is \(S_0\). We assume that, over one period, the share price can either go upwards or downwards. Therefore, we need to find the value of the derivative at time 0 based on the share price at time 1, i.e., \(S_1\).
There are two possibilities for the share price at time \(t = 1\):
$$S_1 =\begin{cases}S_0U,&\text{if the share price goes up}\\S_0D,&\text{if the share price goes down}\end{cases}$$
Where:
U = size of the up move factor bigger than 1.
D = size of the down move factor less than 1.
The possibilities can be shown using a binomial tree as follows:
Figure 1: One-Period Binomial Tree
$$ \begin{array} \hline {} & {} & { S }_{ 0 }U \\ { S }_{ 0 } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix}} \\ {} & {} & { S }_{ 0 }D \\ \end{array} $$
The figure above represents the one-period binomial model for a stock price. Note that it is one period, from time \(t=0\) to \(t=1\) where there are two possible ways where the share price can move either up or down.
Assume that the derivative pays \(c_U\) if the share price goes up and \(c_D\) if it goes down. Consequently, we can take the value of the derivative as a random variable \(C\) which depends on the underlying share’s behavior.
Assume that you hold \(\phi\) units of shares and \(\psi\) units of cash and let \(C_0\) be the value of the derivative today (t=0) and \(r\) be the risk-free rate.
Then at time \(t=1\), the portfolio has a value of:
$$ { C }_{ 1 }=\begin{cases} \phi S_{ 0 }U +\Psi e^{ r }=c_{ U } \text{ If the share price goes up} \\ \phi S_{ 0 }D+\Psi e^{ r }=c_{ D } \text{ If the share price goes down} \end{cases} $$
We can extract the linear equations:
$$\phi S_{ 0 }U +\Psi e^{ r }=c_{ U }……….(1)$$ $$\phi S_{ 0 }D+\Psi e^{ r }=c_{ D }……….(2)$$
Now, solving the two equations above simultaneously, we have:
$$ \phi=\cfrac {c_U-c_D}{S_0 (U-D)} $$
And
$$ \psi=e^{-r} \left[\cfrac {c_D U-c_U D}{U-D}\right] $$
Once we know the values of \(\psi\) and \(\phi\) we can estimate the value of the call option at time \(t=0\) as:
$$ C_0=\phi S_0+\psi $$
If we substitute the value of \(\phi\) and \(\psi\) we have:
$$ \begin{align*} C_0 & =S_0 \left(\cfrac {c_U-c_D}{S_0 (U-D) } \right)+e^{-r} \left[\cfrac {c_D U-c_U D}{U-D} \right] \\ & =\cfrac {1}{U-D} \left[c_U (1-De^{-r} )+c_D (Ue^{-r}-1) \right] \end{align*} $$
Multiplying the numerator and denominator by \(e^r\) we get:
$$ \begin{align*} C_0 &=\cfrac {e^{-r}}{U-D} \left[c_U (e^r-D)+c_D (U-e^r ) \right] \\ & =e^{-r} \left[\cfrac {e^r-D}{U-D} c_U+ \cfrac {U-e^r}{U-D} c_D \right] \end{align*} $$
Now denote
$$ \pi_U=\cfrac {e^r-D}{U-D} $$
And
$$ \pi_D=1-\pi_U=\cfrac {U-e^r}{U-D} $$
The value of the derivative at time \(t=0\) is:
$$ C_0=e^{-r} [\pi_U c_U+(1-\pi_U)c_D ] $$
\(\pi_U\) and \(\pi_D\) are the risk-neutral probabilities of up and down moves, respectively.
Note that the portfolio \((\phi,\psi)\) is the replicating portfolio as discussed before.
The previous section is the basic result of the single period binomial model. It has allowed us to solve the option price without estimating the share price’s probabilities of moving up or down.
Risk neutrality to an investor is a case where the investor is indifferent towards risk. Such an investor understands that risks exist in investment but does not consider it when making the investment choice.
However, in the real world, investors have diverse risk preferences and would often expect returns to be proportional to the level of risk inherent in an investment.
Assuming the risk-neutral approach, however, allows us to determine the correct price of the derivatives. This is because derivatives are priced based on the price of the underlying assets. Therefore, the risk preferences are already reflected in the prices of the underlying assets, which move up and down depending on the level of the investor’s risk aversion.
If we assume that the same risk-free rate of return applies to the expected return on the underlying security and the discount rate used for the expected payoff on the option or any other derivative instrument, then:
$$C_0=e^{-r}\left[\pi_Uc_U+(1-\pi_U)c_D\right]$$
Where:
\(\pi_U\) and \(\pi_D\) represent the risk-neutral probability of an upward and downward movement in the price of the underlying stock as described before.
\(c_U\) and \(c_D\) the expected payoffs from the call when the underlying stock price moves up and down, respectively; and
\(e^{-r\ }\) the discounting factor of the expected payoff at the risk-free rate \(r\).
The above formula is an application of the risk-neutral approach to pricing. To prove this, let us compute the expected stock price as follows:
$$\begin{align}E\left(S_P\right)&=\pi_U S_0 U+\left(1-\pi_U \right)S_0D\\ \Rightarrow E\left(S_P\right)&=\pi_U S_0\left(U-D\right)+S_0D\ldots(ii)\end{align}$$
Recall that:
$$\pi_U=\frac{e^r-D}{U-D}$$
Substituting the value of \(\pi_U\) equation (ii) becomes:
$$\begin{align}E\left(S_P\right)&=S_0\left(e^r-D\right)+S_0D\\&=S_0e^r\end{align}$$
This shows that if we assume the risk-neutral probabilities of an upward or downward movement in the stock price, the underlying stock grows at the risk-free rate of return, justifying the risk-neutral approach to binomial option pricing.
The share price at time 0 is $60. Over a single period, the share price can either move up to $90 or down to $45. The risk-free rate of interest is 5% per time period.
Calculate the value of the one-period European call option, \(C_0\), with an exercise price of $75.
Let us first represent the share price in a binomial tree:
$$ \begin{array} \hline {} & { } & {{ S }_{ 1 }=90} \\ {{ S }_{ 0 }=60} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {{ S }_{ 1 }=45} \\ \end{array} $$
We can also consider the binomial tree for the corresponding payoffs generated by the call option:
$$ \begin{array} \hline {} & { } & {{ C }_{ 1 }=\text{max}(0,90-75)=15} \\ {{ C }_{ 0 }=?} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {{ C }_{ 1 }=\text{max}(0,45-75)=0} \\ \end{array} $$
Now,
$$U=\frac {90}{60}=1.5$$
and
$$D=\frac {45}{60}=0.75$$
So,
$$ \begin{align*} \pi_U & =\cfrac {e^r-D}{U-D}=\cfrac {e^{0.05}-0.75}{1.5-0.75}=0.4017 \\ \Rightarrow \pi_D & =1-0.4017=0.5983 \\ \end{align*} $$
Therefore,
$$ \begin{align*} C_0 & =e^{-r} [\pi_U c_U+(1-\pi_U)c_D ] \\ & =e^{-0.05} [0.4017×15+0.5983×0]=5.7316 \\ \end{align*} $$
To save us time and space, we could have just combined the two previous binomial trees with the payoff at the end of the period written at the below of the share price as below:
$$ \begin{array} \hline {} & { } & \begin{matrix} {{ S }_{ 1 }=90} \\ {{ C }_{ 1 }=\text{max}(0,90-75)=15} \end{matrix} \\ \begin{matrix} {{ S }_{ 0 }=60} \\ {{ C }_{ 0 }=?} \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & \begin{matrix} {{ S }_{ 1 }=45} \\ {{ C }_{ 1 }=\text{max}(0,45-75)=0} \end{matrix} \\ \end{array} $$
The following formula is used to price options in the binomial model where volatility is given:
\(U\)=size of the up move factor \(=e^{(r-\delta)t+\sigma \sqrt {t}}\); and
\(D\)=size of the down move factor= \(=e^{(r-\delta)t-\sigma \sqrt {t}}\).
Where:
\(\sigma\) = the annual volatility of the underlying asset’s returns;
\(t\) = the length of the step in the binomial model; and
\(\delta\) = the continuous dividend yield.
Making \(\pi_U\) the risk-neutral probability of an upward movement in the share price and \(\pi_D\) the risk-neutral probability of a downward movement in the share price:
$$ \begin{align*} \pi_U & =\cfrac {e^{(r-\delta)t}-D}{U-D} \\ \pi_D & =1-\pi_U \\ \end{align*} $$
The price of an exchange-quoted zero-dividend share is $30. Over the past year, the stock has exhibited a standard deviation of 17%. The continuously compounded risk-free rate is 5% per annum.
Compute the value of a 1-year European call option with a strike price of $30 using a one-period binomial model.
We know that:
\(U\)=size of the up move factor \(=e^{(r-\delta)t+\sigma \sqrt {t}}\)
\(D\)=size of the down move factor= \(=e^{(r-\delta)t-\sigma \sqrt {t}}\)
$$ \begin{align*} U&=e^{(r-\delta)t+\sigma \sqrt{t}}=e^{(0.05)1+0.17 \sqrt {1}}=1.2461\\ D&=e^{(r-\delta)t-\sigma \sqrt {t}}=e^{(0.05)1-0.17 \sqrt {1}}=0.8869\\ \Rightarrow \pi_U & =\cfrac {e^{rt}-D}{U-D}=\cfrac {e^{0.05×1}-0.8869}{1.2461-0.8869}=0.4576\\ \pi_D & =1-0.4576=0.5424 \\ \end{align*} $$
The binomial tree for the stock price is therefore as below:
$$ \begin{array} \hline {} & { } & \begin{matrix} {{ S }_{ 1 }=30 \times 1.2461=$37.38} \\ {{ C }_{ 1 }=\text{max}(0,37.38-30)=$7.38} \end{matrix} \\ \begin{matrix} {{ S }_{ 0 }=30} \\ {{ C }_{ 0 }=?} \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & \begin{matrix} {{ S }_{ 1 }=30 \times 0.8869=$26.61} \\ {{ C }_{ 1 }=\text{max}(0,26.61-30)=$0} \end{matrix} \\ \end{array} $$
Then the value of the European call option is:
$$ C_0=e^{-r} \left[\pi_U c_U+(1-\pi_U)c_D \right]=e^{-0.05} [0.4576×7.38+0.5424×0]=$3.2124 $$
The ideas discussed in the one-period binomial model also apply here. Note that for simplicity purposes, we have been assuming the periods are in years. However, it can also be in months or any other timeframe.
This section now extends the thought process to the two-period model, which you will realize is intuitive.
Study the following binomial tree model below for the share price.
Figure 2: The Two-Step Binomial Model
$$ \begin{array} {} & {} & {} & { S }_{ 2 }={S_1 U_1} \\ {} & { S }_{ 1 }={S_0 U_0} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ { S }_{ 0 } \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { S }_{ 2 }={S_1 D_1} \\ \\ { S }_{ 2 }={S_1 U_1} \end{matrix} \\ {} & { S }_{ 1 }={S_0 D_0} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { S }_{ 2 }={S_1 D_1} \\ \end{array} $$
The first year of the two-period binomial model is basically the same as the one-period binomial model.
Let \(\pi_{U_0}\) be the risk-neutral probability for the first year:
$$ \pi_{U_0}=\cfrac {e^{rt}-D_0}{U_0-D_0 } $$
\(\pi_{U_1}\) be the risk-neutral probability for the second year after the share rises in the first year:
$$ \pi_{U_1}=\cfrac {e^{rt}-D_1}{U_1-D_1 } $$
and \(\pi_{U_2}\) be the risk-neutral probability for the second after the share price drops in the first year:
$$ \pi_{U_2}=\cfrac {e^{rt}-D_2}{U_2-D_2 } $$
Then we have:
$$ C_1 (U)=e^{-r} [\pi_{U_1} C_2 {(U_U) }+(1-\pi_{U_1} ) C_2 (U_D)] $$
and
$$ C_1 (D)=e^{-r} [\pi_{U_2} C_2 (D_U )+(1-\pi_{U_2} ) C_2 (D_D)] $$
To find the value of the derivative at time 0, we find the expectation of the values \(C_1(U)\) and \(C_1(D)\). That is:
$$ C_0=e^{-r} [\pi_{U_0} C_1(U)+(1-\pi_{U_0} ) C_1 (D)] $$
The value at time 1 is simply the expectation at time 1 of the derivative payoff at time 2 based on the risk-neutral probability measure.
The notation used herein might be confusing at first but using an example might help. Now, study the binomial tree for the payoff below:
Figure 3: Two-Step Binomial Model for Option Payoffs
$$ \begin{array} {} & {} & {} & { C_2(U_U)} \\ {} & { C }_{ 1 }(U) & \begin{matrix} & { \small {\pi_{U_1}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_1}} } & \end{matrix} & {} \\ { C }_{ 0 } \begin{matrix} & { \small {\pi_{U_0}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_0}} } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { { C_2(U_D)}} \\ \\ { { C_2(D_U)}} \end{matrix} \\ {} & { C }_{ 1 }(D) & \begin{matrix} & { \small {\pi_{U_2}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_2}} } & \end{matrix} & {} \\ {} & {} & {} & { { C_2(D_D)}} \\ \end{array} $$
The share price at time 0 is $60. Over a single period, the share price can either move up to $90 or down to $45. Following the up-movement in the first period, the share price can either move up to $120 or down to $75. Following the downward movement in the first period, the share price can either move up to $60 or down to $37.50. The risk-free rate of interest is 5% per time period.
Calculate the value of the two-period European call option, \(C_0\) with an exercise price of $75.
Consider the following binomial tree:
$$ \begin{array} {} & {} & {} & \begin{matrix} S_{UU}=120 \\ C_{UU}=120-75=45 \end{matrix} \\ {} & \begin{matrix} { S }_{ U }={90} \\ C_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} S_0=60 \\ C_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} S_{UD}=75 \\ C_{UD}=\text{max}(0,75-75)=0 \end{matrix} } \\ \\ { \begin{matrix} S_{DU}=60 \\ C_{DU}=\text{max}(0,60-75)=0 \end{matrix} } \end{matrix} \\ {} & { \begin{matrix} S_D=45 \\ C_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} S_{DD}=60 \\ C_{DD}=\text{max}(0,60-75)=0 \end{matrix} } \\ \end{array} $$
The movement factor for the second period is:
$$ U_1=\cfrac {120}{90}=\cfrac {4}{3} $$
And
$$ D_1=\cfrac {75}{90}=\cfrac {5}{6} $$
Now, the risk-neutral probability is:
$$ \pi_1=\cfrac {e^{-r}-U_2}{U_2-D_2}=\cfrac {e^{-0.05}-\frac {4}{3}}{\frac {4}{3}-\frac {5}{6}}=0.43588 $$
Now, the possible derivative values at the second period if the share prices rise is 45 and 0 then the derivative payoff at the beginning of the second period is:
$$ \begin{align*} C_U & =e^{-r} [\pi_U c_{UU_1}+(1-\pi_1)c_{UD_1} ] \\ & =e^{-0.05} [0.43588×45+(1-0.43588)×0] \\ &=18.658 \\ \end{align*} $$
The movement factors for the second branch (when the share price drops) are equal as above and so as the risk-neutral probability and hence:
$$C_D =e^{-r} [\pi_2 c_{DU_2}+(1-\pi_2)c_{DD_2} ]$$
Where:
$$\begin{align}U_2&=\frac{60}{45}=1.333\\ D_2&=\frac{37.5}{45}=0.8333\\ \pi_2&=\frac{e^{0.05}-0.833}{1.333-0.833}\end{align}$$
Therefore,
$$ C_D =e^{-0.05} [0.43588×0+(1-0.43588)×0] =0 \\ $$
And so,
$$C_0 =e^{-r} [\pi_U c_U+(1-\pi_U)c_D$$
Where:
$$U=\frac{90}{60}=1.5,\ \ D=\frac{45}{60}=0.75\ \text{and}\ \pi_U=\frac{e^{0.05}-0.75}{1.5-0.75}=\ 0.40169$$
Thus,
$$ \begin{align*} C_D &=e^{-0.05} [0.40169×18.658+(1-0.40169)×0] \\ & =7.1293 \\ \end{align*} $$
As you must have realized by now, when the payoffs are zero, it makes the work easier. You may ignore these values to save you time.
A two-year European put has a strike price of $60 on a stock with a current price of $54. A model with two steps has been constructed, and it is expected that the share price will move up or down by 20% at each step. The size of each step is one year. The continuously compounded risk-free rate of return applicable over the contract term is 4% per annum.
Calculate the price of the put option.
Consider the following two-step Binomial-tree:
$$ \begin{array} {} & {} & {} & \begin{matrix} S_{UU}=77.76 \\ P_{UU}=\text{max}(60-77.76,0)=0\end{matrix} \\ {} & \begin{matrix} { S }_{ U }={64.8} \\ P_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} S_0=54 \\ P_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} P_{UD}=75 \\ P_{UD}=\text{max}(0,60-51.84)=8.16 \end{matrix} } \\ \\ { \begin{matrix} S_{DU}=51.84 \\ P_{DU}=\text{max}(60-51.84,0)=8.16\end{matrix} } \end{matrix} \\ {} & { \begin{matrix} S_D=43.2 \\ P_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} S_{DD}=37.5 \\ P_{DD}=\text{max}(60-34.56,0)=25.44 \end{matrix} } \\ \end{array} $$
We apply the same principles as with the call option.
However, we need to note that the put results in a payoff when the underlying asset price falls below the strike price.
$$P_0=\pi P_1U+\left(1-\pi\right)P_1D$$
This can also be written as:
$$P_0=e^{-2r\Delta t}\left[\pi^2P\left(U_U\right)+2\pi\left(1-\pi\right)P\left(U_D\right)+\left(1-\pi\right)^2P(D_D)\right]$$
In this case, the same probabilities of up and down movements apply at each step:
$$\pi=\frac{e^{0.04}-0.8}{1.2-0.8}=0.602$$
Substituting the formula for values:
$$P_0=e^{-2\times0.04\times1}\left[{0.602}^2\times0+2\times0.602\times0.398\times8.16+{0.398}^2\times25.44)\right]=\$ 7.33 $$
We can generalize the two-step binomial model using Figure 3. During each time step, it either moves up to \(U \times \text{Initial value}\) or \(D \times \text{Initial value}\).
Let \(r\) be the risk-free rate of interest and \(\Delta t\) years the length of a period, then we know that:
$$ C_1 (U)=e^{-r\Delta t} [\pi_{U_1} C_2 {U_U}+(1-\pi_{U_1 } ) C_2 (U_D ) ]…………..(1) $$
And
$$ C_1 (D)=e^{-r\Delta t} [\pi_{U_2} C_2 (D_U )+(1-\pi_{U_2} ) C_2 (D_D ) ]…………..(2) $$
We know also that:
$$ C_0=e^{-r\Delta t} [\pi_{U_0} C_1 (U)+(1-\pi_{U_0} ) C_1 (D) ] ………(3)$$
Now, if we assume that \(\pi=\pi_{U_0}=\pi_{U_1}=\pi_{U_2} \) then, substituting equations (1) and (2) in (3), we have:
$$ C_0=e^{-2r\Delta t} [\pi^2 C(U_U )+2\pi (1-\pi)C(U_D )+(1-\pi)^2 C(D_D)] $$
This is consistent with the principle of risk-neutral valuation, that is the variables are \(\pi^2\), \(2\pi(1-\pi)\) and \((1-\pi)^2\) are the probabilities of reaching upper, middle, and lower nodes. This principle will hold as more nodes are added.
Binomial models with one or two steps are unrealistically simple. Assuming only one or two steps would yield a very rough approximation of the option price. In practice, the life of an option is divided into 30 or more time steps. In each step, there is a binomial stock price movement.
As the number of time steps is increased, the binomial tree model makes the same assumptions about stock price behavior as the Black–Scholes–Merton model, which we will see in detail in the next chapter.
When the binomial tree is used to price a European option, the price converges to the Black–Scholes–Merton price as the number of time steps is increased.
Evidently, it is easy to see that constructing a binomial tree is dependent on the calculation of the option payoff and the risk-neutral probability based on the information given.
As stated before, American options can be exercised before the expiry date; therefore, appropriate binomial trees should be constructed.
American-style options can be exercised any time before the expiration date.
The Binomial model allows us to examine the payoff from the option at the end of each node and determine which node the option will result in the maximum payoff and hence, early exercise.
Let us consider an American style call option and consider the following payoffs from a call option
$$ \begin{array} {} & {} & {} & { C_2(U_U)} \\ {} & { C }_{ 1 }(U) & \begin{matrix} & { \small {\pi_{U_1}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_1}} } & \end{matrix} & {} \\ { C }_{ 0 } \begin{matrix} & { \small {\pi_{U_0}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_0}} } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { { C_2(U_D)}} \\ \\ { { C_2(D_U)}} \end{matrix} \\ {} & { C }_{ 1 }(D) & \begin{matrix} & { \small {\pi_{U_2}} } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & {\small {1-\pi_{U_2}} } & \end{matrix} & {} \\ {} & {} & {} & { { C_2(D_D)}} \\ \end{array} $$
American style options can be exercised before expiry. Thus, to compute the price, we check for the value of the option at each node. If the option’s value is greater if exercised, we assign the value to that node. Otherwise, the option is left unexercised, and we work backward on the binomial tree as usual.
At any node, the value of the option is given by:
$$C=\text{max}\left(S_T-K,e^{-r}\left[\pi_Uc_U+\left(1-\pi_U\right)c_D\right]\right)$$
The maximum of the payoff and the option’s value at the node are assigned to a given node. We then proceed backward on the binomial tree as before. The same principles will apply to the corresponding American style put options.
Let us consider an example to make it clear.
A two-year American style put has a strike price of $60 on a stock with a current price of $54. A model with two steps has been constructed, and it is expected that the share price will move up or down by 20% at each step. The size of each step is one year. The continuously compounded risk-free rate of return applicable over the contract term is 4% per annum.
Calculate the price of the put option.
Consider the following binomial tree:
$$ \begin{array} {} & {} & {} & \begin{matrix} \text{Node D:}\\S_{UU}=77.76 \\ P_{UU}=\text{max}(60-77.76,0)=0\end{matrix} \\ {} & \begin{matrix}B\\ { S }_{ U }={64.8} \\ P_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} A\\ S_0=54 \\ P_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} \text{Node E:}\\S_{UD}=75 \\ P_{UD}=\text{max}(0,60-51.84)=8.16 \end{matrix} } \\ \\ { \begin{matrix} \text{Node F:}\\S_{DU}=51.84 \\ P_{DU}=\text{max}(60-51.84,0)=8.16\end{matrix} } \end{matrix} \\ {} & { \begin{matrix} C\\S_D=43.2 \\ P_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} \text{Node G:}\\S_{DD}=37.5 \\ P_{DD}=\text{max}(60-34.56,0)=25.44 \end{matrix} } \\ \end{array} $$
We start at the final nodes and work backward as before. At node B, the value of the option \(P_U\) is given as:
$$P_U=e^{-r\Delta t}\left(\pi P_{UU}+(1-\pi)P_{UD}\right)$$
Where:
$$\pi=\frac{e^{0.04}-0.8}{1.2-0.8}=0.602$$
Therefore,
$$P_U=e^{-0.04\times1}\left(0.602\times0+0.398\times8.16\right)=3.1203$$
The price of the put at this node is $3.1203.
However, the put has zero payoff at this node, i.e.
$$\max{\left(0,60-64.8\right)}=0$$
Thus it would not be optimal to exercise at this node and the value at this node will be:
$$\max{\left(K-S_T,P_U\right)}=\max{\left(0,3.1203\right)}=3.1203$$
Hence, the value assigned to node B is \(P_U=3.1203\).
At node C, the value of the option, \(P_D\) is given as:
$$P_D=e^{-0.04}\left(0.602\times8.16+0.398\times25.44\right)=14.459$$
The option has a payoff from the put at this node is $16.8 calculated as:
$$\max{\left(K-S_T,P_D\right)}=\max{\left(16.8,14.448\right)}=16.8$$
At the initial node, A, the value of the option, \(P_0\) is:
$$e^{-0.04}\left(0.602\times3.1203+0.398\times16.8\right)=8.229$$
The option has a payoff of $6 at this node, and thus early exercise is not optimal.
The option price, \(P_0\), will thus be:
$$P_0=\max{\left(6,8.229\right)}=8.229$$
For American-style options, we check for the value of the option at each node. If the option’s value is greater if exercised, we assign the value to that node. Otherwise, the option is left unexercised, and we work backward on the binomial tree as usual.
A barrier option is an option whose existence depends upon the underlying asset’s price reaching a predetermined barrier level. It can be either:
These types are exercised only if the underlying asset price is below a predetermined value during the term of the option. Then, the payoffs are given by:
$$ \text{Call up}-\text{and}- \text{out option}=\begin{cases} \text{max}(0,S_{ T }-X), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T })\ge B \\ F, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) < B \end{cases} $$ $$ \text{Put up}-\text{and}- \text{out option}=\begin{cases} \text{max}(0,X-S_{ T }), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T })\ge B \\ F, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) < B \end{cases} $$
b. Down-and-out options
In this type, the option can only be exercised if the underlying asset price is higher than the barrier value. The payoffs are given by:
$$ \text{Call down}-\text{and}- \text{out option}=\begin{cases} \text{max}(0,S_{ T }-X), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) > B \\ F, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T })\le B \end{cases} $$ $$ \text{Put down}-\text{and}- \text{out option}=\begin{cases} \text{max}(0,X-S_{ T }), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) > B \\ F, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) \le B \end{cases} $$
II. A knock-in, implying it has no value until the underlying reaches a certain specified price (barrier level). It can be further be subdivided into:
a. Up-and-in options:
This type of barrier options is only exercised when the underlying asset price is above a certain level, say $B during the options life. Let the strike price of the option be X ,then the payoffs of this option at maturity are:
$$ \text{Call up}-\text{and}- \text{in option}=\begin{cases} \text{max}(0,S_{ T }-X), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) \ge B \\ 0, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) < B \end{cases} $$ $$ \text{Put up}-\text{and}- \text{in option}=\begin{cases} \text{max}(0,X-S_{ T }), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) \ge B \\ 0, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) < B \end{cases} $$
b. Down-and-in options
These are types of barrier options which are only exercised at maturity if the underlying asset price falls below a certain predetermined level barrier (B). The prices at the maturity are, therefore:
$$ \text{Call down}-\text{and}- \text{in option}=\begin{cases} \text{max}(0,S_{ T }-X), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) \le B \\ 0, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) > B \end{cases} $$ $$ \text{Put down}-\text{and}- \text{in option}=\begin{cases} \text{max}(0,X-S_{ T }), & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) \le B \\ 0, & \text{if max}(S_{ 1 },S_{ 2 },…S_{ T }) > B \end{cases} $$
The binomial pricing of the barrier is similar to that of the standard option, only that calculations of option payoffs at maturity are dependent on the barrier level.
The current stock price of cooperation is $100. Over the next three months, the stock price could go up to $110 or go down to $90. A down-and-in barrier call option is set on this stock with a strike price of $80 and a barrier value of $100.
The risk free rate of interest is 5%
Calculate the option’s price assuming a one period binomial model
Let start with constructing drawing the binomial tree:
$$ \begin{array} \hline {} & { } & \begin{matrix} { S }_{ 1 }=110 \\ C_1=\text{max}(0,S_T-X),\text{if max}(S_1,S_2,…,S_T)=B=0 \end{matrix} \\ \begin{matrix} { S }_{ 0 }=100 \\ C_0=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & \begin{matrix} { S }_{ 1 }=90 \\ C_1=\text{max}(0,S_T-X),\text{if max}(S_1,S_2,…,S_T) < B=90-80=10 \end{matrix} \\ \end{array} $$
Recall that a down-and-in barrier option is exercised at maturity if the underlying asset price falls below a certain predetermined level barrier (B) and the share price must be less than the barrier value and greater than the strike price; otherwise, it will be worthless.
Now we want to calculate the risk-neutral probability. We know that:
$$ \pi=\cfrac {e^{r\Delta t}-D}{U-D} $$ \(U=\cfrac {110}{100}=1.1\)
\(D=\cfrac {90}{100}=0.9 \)
$$ \Rightarrow \pi=\cfrac {e^{r\Delta t}-D}{U-D}=\pi=\cfrac {e^{0.05×0.25}-0.9}{1.1-0.9}=0.563 $$
We know also that:
$$ C_0=e^{-r\Delta t} [\pi_{U_0} C_1 (U)+(1-\pi_{U_0} ) C_1 (D) ]=e^{-0.05×0.25} [0.56×0+0.437×10]=4.316 $$
As you must have realized, you can easily extend the pricing to a two-period binomial model. So, basically, if you are able to calculate the payoffs at the terminal nodes and working backward the tree as usual.
The same principles also apply to put options.
In an Asian option, the payoff depends on the average price of the underlying asset over a period of time instead of standard options where the payoff is determined by the involvement of the underlying at a specific point in time.
The average can be calculated arithmetically as:
$$ \text{Arithmetic average}=\cfrac {s_1+s_2+⋯+s_n}{n} $$
And geometrically as:
$$ \sqrt [n]{s_1 s_2…s_n } $$
The payoff from the geometric Asian options is given by:
$$ \begin{align*} \text{Call Option}& =\text{max}\left[ { \left( 0,\prod _{ i=1 }^{ n }{ { S }_{ i } } \right) }^{ \cfrac { 1 }{ n } }-K \right] \\ \text{Put Option}& =\text{max}\left[ {0,K- \left(0, \prod _{ i=1 }^{ n }{ { S }_{ i } } \right) }^{ \cfrac { 1 }{ n } }\right] \\ \end{align*} $$
While the payoff from the arithmetic Asian options is given by:
$$ \begin{align*} \text{Call Option} & =\text{max}\left[ 0,{ \left( \frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { S }_{ i } } \right) }-K \right] \\ \text{Put Option} &= \text{max}\left[ 0,K-{ \left( \frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { S }_{ i } } \right) } \right] \\ \end{align*} $$
We shall consider Asian options whose payoffs are dependent on the arithmetic average of the path of the price it takes. Moreover, we will assume that the underlying asset price is a discrete-time stochastic process with the increasing factors given by:
$$U=e^{(r-\delta)t+\sigma \sqrt{t}}$$
and
$$D=e^{(r-\delta)t-\sigma \sqrt{t}}$$
Where
\(\sigma\) = the volatility observed from the data;
\(t\) = the length of one period;
\(r\) = the risk-free rate; and
\(\delta\) = the rate of dividend payment.
The risk-neutral probability is then given by:
$$ \pi=\cfrac {e^{(r-\delta)t}-D}{U-D} $$
The current price of a share is $100. An Asian option is set on this asset with a strike price of $100. The risk-free rate of interest is 8%, \(\sigma\)=0.30, \(\delta\)=0 and \(T\)=1.
Calculate the price of an arithmetic Asian call option using a two-period binomial
Using the forward tree formula, we have:
$$ \begin{align*} u & =e^{ \frac {(0.08)}{2} + \frac {0.3}{\sqrt {2}} }=1.2868 \\ d & =e^{ \frac {0.08}{2}-\frac {0.3}{\sqrt {2}} } =0.84187 \\ \end{align*} $$
The risk-neutral probabilities are:
$$\pi_u=\frac{e^{0.08\times0.5}-0.84187}{1.2868-0.84187}=0.4471$$
and
$$1-\pi_u=1-0.4471=0.5529$$
We can now comfortably construct the period binomial tree:
$$ \begin{array} \hline {} & {} & {} & {} & { S }_{ 2 }=165.59 \\ {} & {} & { S }_{ 1 }=100 \times 1.2868=128.68 & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} { S }_{ 0 }=100 \\ V_0=? \end{matrix} & {\begin{matrix} \\ \begin{matrix} \begin{matrix} \Huge \nearrow \\ \end{matrix} \\ \Huge \searrow \end{matrix} \\ \end{matrix} } & {} & {} & { S }_{ 2 } =108.34 \\ {} & {} & { S }_{ 1 }=100 \times 0.8419=84.19 & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & {} & { S }_{ 2 }=70.84 \\ \end{array} $$
From the tree above, the two possible prices in the first year are 128.68 and 84.19 and 165.59,108.34 and 70.84 in the last year. The possible averages are:
\(\cfrac {128.68+165.59}{2}=147.135,\cfrac {128.68+108.34}{2}=118.51 ,\cfrac {84.19+70.84}{2}=77.515\)
and \(\cfrac {84.19+108.34}{2}=96.26\)
Now, using the strike price of X=100, the “Up” value is \(147.135-100=47.135\), and the “Down” value is \(118.51-100=18.51\).
Then the value of the option is:
$$ V_0=e^{-0.08}\left({0.4471^2}^2\times 47.135+2\times 0.4471\times 0.5529\times 18.51\right)=17.14681$$
We can easily change from the arithmetic mean to geometric, which by now should be intuitive. Moreover, if we are not given the volatility, we could easily adjust the formula by omitting it.
Like options on share prices, we can construct binomial trees for other assets such as stock indices with continuous dividends, currencies, and futures contracts.
Consider a stock paying a dividend yield at a rate of \(q\) with a risk-free rate of interest \(r\). This implies that the capital gain is \(r-q\). If the stock price starts at \(S_0\), then the expected value after a period length of \(\Delta t\) must be \(S_0 e^{(r-q)\Delta t}\).
This means that:
$$ \pi S_0 U+(1-\pi) S_0 D=S_0 e^{(r-q)\Delta t} $$
Where:
\(\pi=\cfrac {e^{(r-q)\Delta t}-U}{U-D}\)
We simply now use \(e^{(r-q)\Delta t} \) instead of \(e^{r\Delta t}\).
Given the volatility of \(\sigma\), the up and down factor movements are can be computed as: \(U=e^{(r-q)\Delta t+\sigma\sqrt{\Delta t}}\) and \(D=e^{(r-q)\Delta t-\sigma\sqrt{\Delta t}}\).
For a stock with continuously payable dividends, the up and down factor formulas are adjusted as follows:
$$U=e^{(r-q)\Delta t+\sigma\sqrt{\Delta t}}$$
and
$$D=e^{(r-q)\Delta t-\sigma\sqrt{\Delta t}}$$
A stock currently has a price of $81 and has a dividend yield of 2%. A one-year European call option has been issued on this stock with a strike price of $80. The continuously compounded risk-free rate of return is 4%, and the stock has a volatility of 20%.
Calculate the price of the call using a two-period binomial tree.
We construct the Binomial tree as follows:
$$ \begin{array} {} & {} & {} & \begin{matrix} \text{Node D:}\\S_{UU}=107.48 \\ C_{UU}=\text{max}(107.48-80,0)=27.48\end{matrix} \\ {} & \begin{matrix}B\\ { S }_{ U }=93.30\\ C_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} A\\ S_0=81 \\ C_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} \text{Node E:}\\S_{UD}=81 \\ C_{UD}=\text{max}(81-80, 0)=1 \end{matrix} } \\ \\ { \begin{matrix} \text{Node F:}\\S_{DU}=81 \\ C_{DU}=\text{max}(81-80)=1 \end{matrix} } \end{matrix} \\ {} & { \begin{matrix} C\\S_D=70.32 \\ C_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} \text{Node G:}\\S_{DD}=61.04 \\ C_{DD}=\text{max}(61.04-80,0)=0 \end{matrix} } \\ \end{array} $$
We compute the value of U and D.
$$U=e^{(r-q)\Delta t+\sigma\sqrt{\Delta t}}=e^{(0.04-0.02)0.5+0.2\sqrt{0.5}} = 1.1635$$
and
$$D=e^{(r-q)\Delta t+\sigma\sqrt{\Delta t}}=e^{(0.04-0.02)\times0.5-0.2\sqrt{0.5}} = 0.8768$$
Next, we compute, \(\pi\) the risk-neutral probability
$$\pi=\frac{e^{\left(r-q\right)\Delta t}-U}{U-D}=\frac{e^{\left(0.04-0.02\right)\times0.5}-0.8768}{1.1635-0.8768}=0.4648$$
The option price is computed using the two-step binomial formula as follows:
$$\begin{align}C_0&=e^{-2r\Delta t}\left[\pi^2C\left(U_U\right)+2\pi\left(1-\pi\right)C\left(U_D\right)+\left(1-\pi\right)^2C(D_D)\right]\\ & e^{-2\times0.04\times0.5}\left[{0.4648}^2\times27.48+2\times0.4648\times0.5352\times1+0\right]\\ &=\$ 5.936\end{align}$$
Foreign currency can be referred to as an asset providing a yield at the foreign risk-free rate of interest of \(r_f\). Such options are characterized by two risk-free rates of return applicable in the jurisdictions to which the currency belongs.
For instance, if we are given that; the risk-free rate of return in Australia is 7%, the risk-free rate in the US is 5%, and one Australian dollar exchanges for 0.65 US Dollars on a US Dollar-denominated exchange, then we can compute the price of an option on this exchange rate as before but use the term \(e^{(r-r_f)\Delta t}\) instead of \(e^{r \Delta t}\) in the formula for estimating the risk-neutral probabilities.
In this case, \(r\) will represent the risk-free rate in the US, \(r_f\) will represent the risk-free rate in Australia, and \(\Delta t\) the size of each step as before.
Given the volatility, the up and down factors are computed as:
$$U=e^{(r-r_f)\Delta t+\sigma\sqrt{\Delta t}}$$
$$D=e^{(r-r_f)\Delta t-\sigma\sqrt{\Delta t}}$$
Thus,
$$\pi=\frac{e^{(r-r_f)\Delta t}-D}{U-D}$$
The price of a call option using the two-step binomial is then computed as:
$$\begin{align}C_0&=\pi C_1\left(U\right)+\left(1-\pi\right)C_1(D)\\ &=e^{-2r\Delta t}\left[\pi^2C\left(U_U\right)+2\pi\left(1-\pi\right)C\left(U_D\right)+\left(1-\pi\right)^2C(D_D)\right]\end{align}$$
The US Dollar is currently worth 0.83 Euros. The exchange rate between the two currencies is subject to the volatility of 15%. The risk-free rate of return in the US is 6%, and the risk-free rate in Europe is 4%. A 6-month European call option has been written on this exchange with a strike price of 0.85 Euros.
Calculate the price of this option using the two-step binomial model.
Consider the following the binomial tree:
$$ \begin{array} {} & {} & {} & \begin{matrix} \text{Node D:}\\S_{UU}=0.964 \\ C_{UU}=\text{max}(0.964-0.85,0)=0.114\end{matrix} \\ {} & \begin{matrix}B\\ { S }_{ U }=0.895\\ C_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} A\\ S_0=0.83 \\ C_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} \text{Node E:}\\S_{UD}=0.83 \\ C_{UD}=\text{max}(0.83-0.85, 0)=0 \end{matrix} } \\ \\ { \begin{matrix} \text{Node F:}\\S_{DU}=0.83 \\ C_{DU}=\text{max}(83-0.85,0)=0 \end{matrix} } \end{matrix} \\ {} & { \begin{matrix} C\\S_D=0.77 \\ C_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} \text{Node G:}\\S_{DD}=0.714 \\ C_{DD}=\text{max}(0.714-0.85,0)=0 \end{matrix} } \\ \end{array} $$
We first compute the values of \(U\) and \(D\):
$$U=e^{(0.04-0.06)\times0.25+0.15\times\sqrt{0.25}}=1.0725$$
and
$$D=e^{(0.04-0.06)\times0.25-0.15\times\sqrt{0.25}}=0.9231$$
Next, we compute the risk-neutral probabilities
$$\pi=\frac{e^{\left(0.04-0.06\right)\times0.25}-0.9231}{1.0725-0.9231}=0.4813$$
The option price is computed using the two-step binomial formula as follows:
$$\begin{align}C_0&=e^{-2r\Delta t}\left[\pi^2C\left(U_U\right)+2\pi\left(1-\pi\right)C\left(U_D\right)+\left(1-\pi\right)^2C(D_D)\right]\\ &=e^{-2\times0.04\times0.25}\left[{0.4813}^2\times0.114+2\times0.4813\times\left(1-0.4813\right)\times0\right]\\&=\$ 0.0259\end{align}$$
There are no costs for an investor to take a long or a short position in a futures contract. It follows that in the risk-neutral world, a future price should have an expected growth rate of zero. Using the same notations in non-dividend shares as discussed above and let \(F_0\) is the initial futures price, the expected future price at the end of one period of length \(\Delta t\) should also be \(F_0\) then it follows that:
$$ \pi F_0 U+(1-\pi) F_0 D=F_0 $$
Where
\(\pi=\cfrac {1-D}{U-D} \)
An investor has purchased a one-year call option on an underlying futures contract. The current price of the futures is $40. Over two 6-month steps, the futures price can either go up or down by 10%. The strike price for the call is $42, and the continuously compounded risk-free rate of return applicable over the contract term is 5% per annum.
Calculate the price of the call option.
Consider the following binomial tree:
$$ \begin{array} {} & {} & {} & \begin{matrix} \text{Node D:}\\F_{UU}=48.4 \\ C_{UU}=\text{max}(48.4-42,0)=6.40\end{matrix} \\ {} & \begin{matrix}B\\ { F }_{ U }=44\\ C_U=? \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ \begin{matrix} A\\ F_0=40 \\ C_0=? \end{matrix} \begin{matrix} & {} & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {} \\ \\ { } \end{matrix} & \begin{matrix} { \begin{matrix} \text{Node E:}\\F_{UD}=39.6 \\ C_{UD}=\text{max}(39.6-42, 0)=0 \end{matrix} } \\ \\ { \begin{matrix} \text{Node F:}\\F_{DU}=39.6 \\ C_{DU}=\text{max}(39.6-42,0)=0 \end{matrix} } \end{matrix} \\ {} & { \begin{matrix} C\\F_D=36 \\ C_D=? \end{matrix} } & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {} & { \begin{matrix} \text{Node G:}\\F_{DD}=32.4\\ C_{DD}=\text{max}(32.4–42,0)=0 \end{matrix} } \\ \end{array} $$
Given the percentage increase, the values of U and D are determined as:
$$\begin{align} U&=1.1\\ D&=0.9\end{align}$$
Next, we compute the risk-neutral probabilities
$$\pi=\frac{1-0.9}{1.1-0.9}=0.5$$
The price of the call option can then be computed using the two-step binomial formula as:
$$\begin{align} C_0&=e^{-2r\Delta t}\left[\pi^2C\left(U_U\right)+2\pi\left(1-\pi\right)C\left(U_D\right)+\left(1-\pi\right)^2C(D_D)\right]\\ &=e^{-2\times0.05\times0.5}\left[{0.5}^2\times6.4\right]\\ &=\$1.52\end{align}$$
You will note that we have computed the price based on the increase in the forward price only over the two steps because all the other nodes lead to a payoff of zero.