Investment Risk and Project Analysis

After completing this reading, you should be able to:

1. Discuss the advantages and disadvantages of different measures of investment risk.

• Understand the properties, advantages, and disadvantages of the various measures of investment risk: Variance, Semi Variance, Value at Risk (VaR), and Tail Value at Risk (TVaR).
• Calculate the risk measures above and use them to compare investment opportunities.

2. Conduct risk analysis.

• Understand the following methods to conduct risk analysis: sensitivity analysis, break-even analysis, scenario analysis, and Monte Carlo simulation.
• Use a decision tree to model future outcomes and analyze real options embedded in a project

Measures of Investment Risk

Variance of Return

Variance measures the volatility of stock returns from the expected value.

We shall consider continuous and discrete return distributions. Denote the return of investment by random variable \(X\).

In the case of continuous distributions, the variance of return is given as:

$$ \int _{ -\infty }^{ \infty }{ { \left( \mu -x \right) }^{ 2 }f\left( x \right) dx } $$

Where:

\(\mu\) = the mean return of the investment at the end of the predetermined period; and
\(f(x)\) = the probability density function of the return.

In the case of the discrete distribution of return, the variance is defined as:

$$ \sum _{ \forall x }^{ }{ { { \left( \mu -x \right) } }^{ 2 } } Pr(X=x) $$

Where \(\mu\) represents the mean return of the investment at the end of the predetermined period.

From basic probability, variance can also be defined as:

$$Var\left(X\right)=\sigma_X^2=E\left[X^2\right]-\left(E\left[X\right]\right)^2$$

The standard deviation (square root of variance) is also used in measuring investment risk. That is:

$$\sigma_X=\sqrt{\sigma_X^2}=\sqrt{Var\left(X\right)}$$

Generally, the higher the variance, the more volatile the investment return, and hence the more risky the investment will be.

Example: Calculating the Variance of Return-Discrete Distribution

The returns on an investment are assumed to follow the distribution below:

$$ \begin{array}{c|c} \textbf{Return (%)} & \textbf{Probability} \\ \hline \text{5} & \text{0.05} \\ \text{-7} & \text{0.95} \\ \end{array} $$

Calculate the variance of the investment return.

Solution

$$ var[X]=E[X^2 ]-(E[X])^2 $$ So, $$ \begin{align*} E[X] & =5×0.05+ -7×0.95=-6.4 \\ E[X^2] & =5^2×0.05+(-7)^2×0.95=47.8 \\ \Rightarrow var[X] & =47.8-(-6.4)^2=6.84\%\% \\ \end{align*} $$

Example: Calculating the Variance of Return-Continuous Distribution

The annual investment return is assumed to be modelled by the following function:

$$ f\left( x \right) =\begin{cases} \frac { x }{ 2 } , & 0 < x < 2 \\ 0, & \text{elsewhere} \end{cases} $$

Calculate the variance of the investment returns

Solution

The variance is given by:

$$ \begin{align*} var[X] & =E[X^2 ]-(E[X] )^2 \\E\left( X \right) & =\int _{ -\infty }^{ \infty }{ xf\left( x \right) dx= } \int _{ 0 }^{ 2 }{ x\ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 3 } }{ 6 } \right] }_{ x=0 }^{ x=2 }=\frac { 4 }{ 3 } \\E\left( X^2 \right)& =\int _{ -\infty }^{ \infty }{ x^2 f\left( x \right) dx= } \int _{ 0 }^{ 2 }{ x^2 \ast \frac { x }{ 2 } \ast dx } ={ \left[ \frac { { x }^{ 4 } }{ 8 } \right] }_{ x=0 }^{ x=2 }=2 \\ \Rightarrow Var \left(X \right) & = 2 – {\left( \frac {4}{3}\right)}^ 2 = \frac {2}{3} \end{align*} $$

Alternatively, since \(\mu =E(X)=\frac{4}{3}\) is equal to the mean of the investment return, we could use the formula:

$$ \int _{ -\infty }^{ \infty }{ { \left( \mu -x \right) }^{ 2 }f\left( x \right) dx= } \int _{ 0 }^{ 2 }{ { \left(\frac{ 4 }{ 3 }- x \right) }^{ 2 }\times \frac { x }{ 2 } \times dx } =\frac { 2 }{ 3 } $$

Advantages of Variance as a Measure of Risk

1. Variance is mathematically understandable.
2. Variance leads to appropriate solutions for optimal portfolios under the pretext of mean-variance portfolio theory.

Disadvantages of Variance as a measure of Risk

1. Variance does not quantify the downside risk of a project: It treats all the deviations around the mean as the same regardless of their direction (positive/negative).
2. Variance only measures total risk and does not highlight the maximum possible loss from a project, which may be important to an investor rather than just the total risk.

Semi-variance of Return

An investor may be interested in determining the downside risk rather than just the total risk of a project. The semi-variance of return provides a way of measuring the downside risk of an investment.

For a continuous random variable, semi-variance of return is defined as:

$$ \int _{ -\infty }^{ \mu }{ { \left( \mu-x \right) }^{ 2 }f\left( x \right) dx } $$

In the case of discrete distribution, semi-variance of return is given by:

$$ \sum _{ x < \mu }^{ }{ { { \left( \mu -x \right) } }^{ 2 } } Pr(X=x) $$

If the investment is assumed to be normally distributed, then the semi-variance of the investment returns is perfectly half of the variance.

Example: Calculating the Semi-Variance of Return

The returns on an investment are assumed to follow the distribution below:

$$ \begin{array}{c|c} \textbf{Return (%)} & \textbf{Probability} \\ \hline \text{5} & \text{0.05} \\ \text{-7} & \text{0.95} \\ \end{array} $$

Calculate the semi-variance of the investment return.

Solution

We know that:

$$\mu=E(X)=5\times 0.05+-7\times0.95=-6.4$$

Semi variance only considers the observations below the mean.

So, we need:

$$ \sum _{ x < -6.4 }^{ }{ { { \left( \mu -x \right) } }^{ 2 } } Pr(X=x)=(-6.4+7)×0.95=0.342\% \%pa $$

Advantages of Semi-Variance

1. Semi variance provides a means of estimating the downside risk of a project.

Disadvantages of Semi-Variance

1. Semi variance is not easy to handle mathematically.
2. Semi variance does not take into account the variability above the mean.

Value at Risk (VaR)

VaR is defined as the maximum amount of loss, under normal business conditions, that can be incurred with a given confidence level.

It can also be viewed as the worst possible loss under normal conditions over a specified period.

Suppose an analyst calculates the monthly VaR as $100 million at 95% confidence: What does this imply?

This simply means that under normal conditions, in 95% of the months, we expect the fund to make a profit or lose no more than $100 million. Put differently, the probability of losing $100 million or more in any given month is 5%.

Value at risk gives a statistical sense of measuring the downside risk by a generalization of the likelihood of underperforming investment risk.

For a continuous distribution of investment returns, it is defined as:

$$ Var(X)=-k \text{ where } Pr(X < k)=p $$

For the discrete distribution, value at risk is defined as:

$$ Var(X)=-k \text { where } k=max \left\{x: Pr(X < k)\le p \right\} $$

Value at risk looks at the potential losses on a given portfolio over a future time period with a given degree of confidence. For instance, if we assume a 95% confidence level, then VaR is the amount of loss surpassed only five times in a hundred over a given period. So, we would want to find the probability \( P(X < k)=0.05 \).

Therefore, a positive VaR (a negative \(k\)) shows a loss on an investment. A negative VaR (a positive \(k\)) shows a profit.

Note also that, value at risk is expressed in monetary terms and not as a percentage.

Example: Calculating the VaR of a Project: Discretely Distributed Returns

The distribution of returns for a given investment is shown in the table below. It is given that $10m has been invested in the investment portfolio.

Calculate the VaR over one year given a 95% confidence level

$$ \begin{array}{c|c} \textbf{Return (%)} & \textbf{Probability} \\ \hline \text{5} & \text{0.03} \\ \text{-7} & \text{0.97} \\ \end{array} $$

Solution

First, we need to find the value of k. We know that:

$$ k=max \left\{x: Pr(X < k )\le p \right\} $$

So,

$$ Pr(X < -5)=0 \text { and } P(X < 7)=0.03 \Rightarrow k=7 $$

Note that k is the percentage of investment return, so the 95% VaR per year on a $10m investment is \($10×-0.07=-0.7m\). This means that we are 95% confident that we will not make a profit of less than $700,000 over the next year.

Example: Calculating the VaR of a project :Continuously Distributed Investment Return

The returns for a given financial year for a given investment are assumed to be normally distributed with mean and standard deviation equal to 8%.

Calculate the 97.5% value at risk over a year of a portfolio consisting of $20 million invested in the analyst’s portfolio.

Solution

We need to find the value of \(k\) such that:

$$ \begin{align*} & Pr(X < k)=0.025 \text { where } X\sim N(8,8^2) \\ & \Rightarrow Pr \left(Z < \frac {k-8}{8} \right)=0.025 \\ & \therefore \phi \left( \frac {k-8}{8} \right)=0.025 \\ \end{align*} $$

Using the normal tables, we know that \(\phi (-1.96)=0.025\).

$$ \Rightarrow \frac {k-8}{8}=-1.96 \therefore k=(-1.96)(8)+8=-7.68 $$

\(k\) is the percentage of investment return. Thus, the 97.5% VaR over one year on a $20 million investment portfolio is \(20×7.68\%=1.536m\). This implies that we are 97.5% certain that we will not lose above $1.536 million over the coming year.

Advantages of VaR

1. Value at risk summarizes the risks of a portfolio of a given institution into one number.
2. It is a measure that can be applied across all the financial instruments and portfolios.
3. Value at risk considers the interrelationships between different risk factors.
4. Value a risk can be measured in both price units and the percentage of portfolio value.

Disadvantages of VaR

1. It does not describe the worst possible loss. Indeed, as seen from the example above, we would expect the $100 million loss mark to be breached five times out of a hundred for a 95% confidence level.
2. VaR does not describe the losses in the left tail (i.e., the large negative losses). It indicates the probability of a value occurring but stops short of describing the distribution of losses in the left tail.
3. Two arbitrary parameters are used in its calculation – the confidence level and the holding period. The confidence level indicates the probability of obtaining a value greater than or equal to VaR. The holding period is the time span during which we expect the loss to be incurred, say, a week, month, day, or year. VaR increases at an increasing rate as the confidence level increases. VaR also increases with increases in the holding period.
4. VaR estimates are subject to both model risk and implementation risk. Model risks arise from incorrect assumptions, while implementation risk is the risk of errors from the implementation process.

Tail Value at Risk

The disadvantage of VaR is that it does not quantify the size of the tail. To address this, the tail value at risk focuses on the adverse tail of a probability distribution. It is also referred to as conditional tail expectation.

To define the Tail Value at Risk (Tail VaR), we first define the expected shortfall, which is closely related to the Tail VaR.

For continuous distributions, the expected shortfall is given as

$$ \text{Expected Shortfall} =E \left[max(B-x,0) \right]=\int _{ -\infty }^{ B }{ \left( B-x \right) f\left( x \right)dx } $$

Where \(B\) is a chosen benchmark Level.

For a discrete distribution of investment return, the expected shortfall is given to be:

$$ \text{Expected Shortfall} =E[max(B-x,0) ]=\sum _{ x < B }^{ }{ \left( B-x \right) Pr(X=x) } $$

Where \(B\) is taken to be a certain percentile point on the distribution. For instance, the \((1-p)\) Tail VaR is the expected shortfall in the lower tail. For example, a 95% confidence interval corresponds to the expected loss above the 5% lower tail value.

Example: Calculating the Tail Value at Risk of a Project: Discretely Distributed Returns

$20 has been invested in a portfolio whose return distribution is shown in the table below.

$$ \begin{array}{c|c} \textbf{Return (%)} & \textbf{Probability (Pr(X=x))} \\ \hline \text{4} & \text{0.03} \\ \text{7} & \text{0.97} \\ \end{array} $$

Calculate the tail value at risk of the portfolio over a year given a benchmark level of 5%.

Solution

We know that:

$$ \begin{align*} \text{Tail Value at Risk} & =E[max(B-x,0) ]=\sum _{ x < B }^{ }{ \left( B-x \right) Pr(X=x) } \\ & =E[max(5-x,0]=\sum _{ x < 5 }^{ }{ \left( B-x \right) Pr(X=x) } \\ & =(0.05-0.04)×0.03=0.0003 \\ \end{align*} $$

Thus, on a portfolio of $20 million ,the 95% Tail VaR is \(20×0.0003=0.006\text{ million}\). This can be interpreted as, the amount of decrement of the profits below 5% is $6000.

The merits and demerits of Tail Var are more or less that of VaR, but Tail VaR is more superior to the former because of the following:

1. It meets all the desirable qualities of a coherent risk measure, including subadditivity
2. It has less restrictive assumptions regarding risk/return decision rules
3. Unlike the VaR, TailVaR gives an estimate of the magnitude of a loss for unfavorable events

Properties of a Coherent Risk measure

A risk measure summarizes the entire distribution of dollar returns \(X\) by one number, \(Pr(X)\) There are four desirable properties every risk measure should possess. These are:

1. Monotonicity: \(X_1 \le X_2\),then \(Pr(X_1) \ge Pr(X_2)\)
   Interpretation: If a portfolio has systematically lower values than another, in each state of the world, it must have a greater risk.
2. Subadditivity: \(Pr(X_1+X_2) \le Pr(X_1)+Pr(X_2)\)
   Interpretation: When two portfolios are combined, their total risk should be less than (or equal to) the sum of their individual risks. Merging of portfolios ought to reduce risk.
3. Homogeneity: \(Pr(kX)=kPr(X)\)
   Interpretation: Increasing the size of a portfolio by a factor \(k\) should result in a proportionate scale in its risk measure.
4. Translation invariance: \(Pr(X+h)=Pr(X)-h\)
   Interpretation: Adding cash \(h\) to a portfolio should reduce its risk by \(h\). Like X, \(h\) is measured in dollars.

Example: Properties of Coherent Risk Measures

Ann Conway has spent the last several months trying to develop a new risk measure to appraise a set of default-able zero-coupon bonds owned by her employer. Before its use, her supervisor has asked her to demonstrate that it is a coherent risk measure. The results are listed below:

Given:

• \(x\) and \(y\) are state-contingent payoffs of two different bond portfolios
• \(P(x)\) and \(P(y)\) are risk measures for portfolio \(x\) and portfolio \(y\), respectively.
• \(K\) and \(l\) are arbitrary constants, with \(k>0\).

Determine which of the following equations shows that Conway’s risk measure is not coherent

1. \(P(kx)=kP(x)\)
2. \(P(x)+P(y) \ge P(x+y)\)
3. \(P(x) \le P(y) \text { if } x \le y\)
4. \(P(x+l)=P(x)-l\)
5. None of the above

The correct answer is C.

Option C shows that the risk measure does not satisfy the monotonicity property. Monotonicity requires that \(P(x) \ge P(y) \text { if }x \le y\). If a portfolio has systematically lower values than another, it must have a greater risk in each state of the world.

Risk Analysis

Companies are faced with the challenge of limited capital and have to decide how to invest this limited capital between different investment projects.

When making decisions on which capital projects to finance or invest in, companies are majorly influenced by the relative attractiveness of a project based on risk and return.

Once desirable projects meeting the company’s benchmark return or net present value have been identified, it is necessary to assess how the returns or net present values of these projects would be affected by changes in underlying assumptions, events, or market-wide factors.

The process of analyzing the project’s response to the underlying factors and assessment of the potential impact these factors may have on the net present values or future returns of the projects is known as risk analysis.

Methods of Conducting Risk Analysis

1. Sensitivity analysis or “what if” analysis

This provides a range of possible outcomes as specific assumptions are changed.

It applies to all projects with quantified benefits and costs and tests which variables are essential to the expected outcomes of a project

This method involves recomputing the project outcomes for different values of the main variables and combinations. For instance, sensitivity analysis may be used to check the effect of a change in an assumption, say revenues, on the overall profit.

The procedure of conducting sensitivity analysis is as follows:

1. Determined the key variables and possible changes of a project;
2. Recalculate the variables, for example, NPV; and
3. Calculate the “Switching Value.”

Switching value is the value of a variable arising from a change in the investment decision, and it is usually a percentage change from the initial value of the variable. For example, the switching value for the Net Present Value of a project at a given discount rate can be given to be:

$$ \text {Switching Value}=100\% × \cfrac {NPV^{*}-NPV^0}{NPV^0 } $$

Where \(NPV^0\) is the initial value and \(NPV^{*}\) is the new value.

Example: Sensitivity Analysis

A project requires an initial capital outlay of $100,000. After the initial investment, the company will incur staff costs at the rate of $75,000 per year payable in arrears. The project lifetime is estimated to be five years and is expected to generate a total income of $105,000 at the end of each year. The assumed discount rate is 8% per annum.

Calculate the impact on the overall net present value if the discount rate is increased by 4%.

Solution

We first calculate the project’s Net Present Value, using the 8% discount rate given by:

$$NPV=\text{Present Value of Income}-\text{Present Value of the Costs}$$

Now,

$$\text{PV of costs}=100+75\times PVAF_{@8\%}$$

Where \(PVAF_{@8\%}\) is the present value annuity factor at the given discount rate for the given period, in this case, 5 years. Thus,

$$\text{PV of costs}=100+75\times \frac{(1-{1.08}^{-5})}{0.08}=75\times3.9927=399.453$$

Also,

$$\begin{align}\text{PV of Income} &= \text{Income}\times {PVAF}_{@8\%}\\ & =105\times3.9927=419.23\end{align}$$

Therefore, the NPV of the project at 4% is:

$$419.124-399.453=19.67$$

At a 12% discount rate, \({PVAF}_{@12\%}=3.605\).

Thus,

$${NPV}_{@12\%}=(-100-75)\times3.605+105\times3.605=8.15\ $$

This means that for a 50% increase in the discount rate, the NPV of the project decreases by 58.6%.

The other variables can also be tested to deduce their impact on the project’s net present value. For instance, the project analyst may test the effect of increased staff costs on the overall NPV, or the impact of the revenues on the NPV.

The task is usually to identify the variable whose change significantly affects a project’s expected future outcomes. Once this has been identified, actions will be formulated on how the variable will be handled to ensure the project’s sustenance.

2. Break-even Analysis

Break-even analysis is a financial indicator that shows the relationship between fixed costs, variable costs, and revenue. It is majorly associated with the break-even point, which is when no profit or loss is made from the investment. Break-even analysis can be represented either graphically or calculated mathematically.

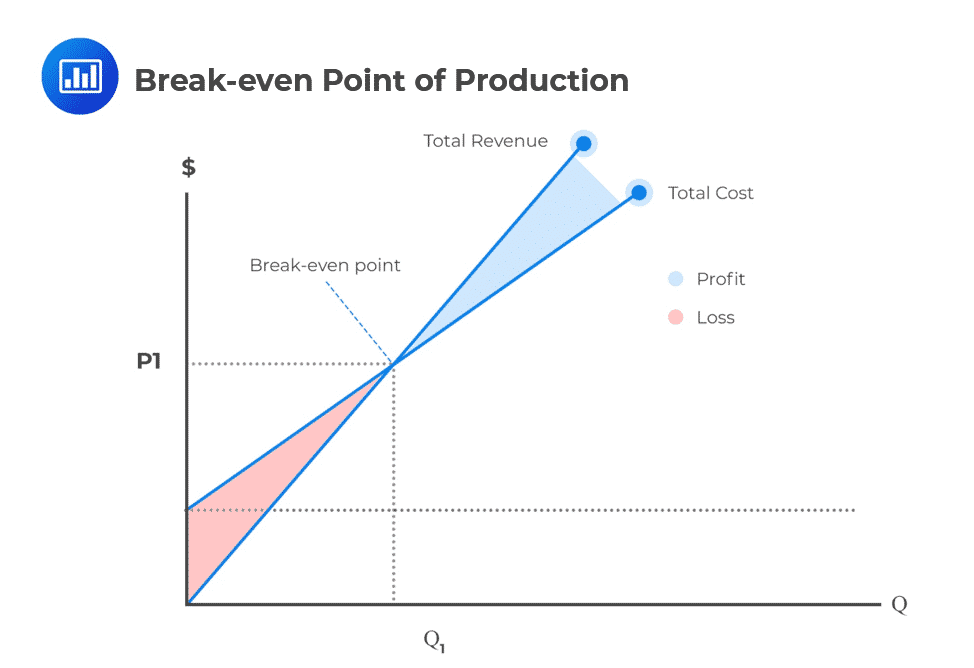Regarding capital budgeting, break-even analysis is concerned with determining the break-even level of input at which the net present value of a project is equal to zero. An example of a break-even level technique is the internal rate of return. This is the rate of return at which the NPV of a project is equal to zero

In accounting, break-even analysis computes the amount of production at a given price intended to cover all the costs experienced. ‘Break-even quantity of sales’ refers to the number of units of a company’s product that is produced and sold, at which point the company’s net income becomes zero.

Computing Breakeven Quantity of Sales

At the point at which a company’s net income is zero, its revenues equal its costs. The company’s costs are variable operating costs, fixed operating costs, and fixed financing costs.

With this in mind, if \(\text{revenue} = \text{costs}\), then

$$ PQ = VQ + F + C $$

Where:

\(P\) = price per unit
\(Q\) = number of units produced and sold
\(V\) = variable cost per unit
\(F\) = fixed operating costs
\(C\) = fixed financing costs

Therefore, if \(Q_{BE}\) is the breakeven quantity of sales, then:

$$ PQ_{BE} = VQ_{BE} + F + C $$

And

$$ Q_{BE}=\cfrac {F+C}{P-V} $$

In other words, a company’s break-even quantity of sales is equal to the sum of the company’s fixed operating and financing costs divided by its unit contribution margin or the difference between the price per unit and variable cost per unit.

A simplification of the break-even quantity of sales is the operating break-even quantity of sales.

At this stage, the revenues from the project equal to cost and the operating break-even quantity of sales is:

$$ Q_{OBE}=\cfrac {F}{P-V} $$

Where P, V and F are as defined previously and \(Q_{OBE}\) represents the operating break-even quantity of sales.

Care should be taken not to confuse the two.

Example: Calculating the Break-Even Quantity of Sales

Assume a company’s product costs are represented by the figures below.

$$ \begin{array}{l|r} \textbf{Price per Unit Sold} & \text{\$8.00} \\ \textbf{Variable Cost per Unit} & \text{\$4.00} \\ \textbf{Fixed Cost} & \text{\$2,500.00} \\ \textbf{Fixed Financing Cost} & \text{\$1,200.00} \\ \end{array} $$

(i) Calculate the company’s break-even quantity of sales.

(ii) Determine the company’s net income at various sales levels

Solution

(i) The formula gives the break-even quantity of sales:

$$\begin{align}Q_{BE}&=\frac{F+C}{P-V}\\ \\ &=\frac{2500+1200}{8-4}=925\text{units}\end{align}$$

(ii) At different sales levels, the net income is as follows in the table:

$$ \begin{array}{c|c|c} \textbf{Units Sold} & \textbf{Sales} & \textbf{Net Income}\\ \hline \text{625} & \text{5,000} & \text{-1,200} \\ \text{725} & \text{5,800} & \text{-800} \\ \text{825} & \text{6,600} & \text{-400} \\ \text{925} & \text{7,400} & \text{0} \\ \text{1,025} & \text{8,200} & \text{400} \\ \text{1,125} & \text{9,000} & \text{800} \\ \text{1,225} & \text{9,800} & \text{1,200} \\ \end{array} $$

As can be seen from the table, at the break-even quantity of sales, net income = 0, below the break-even quantity of sales, net income < 0, and above the break-even quantity of sales, net income > 0.

Example: Calculating the Break-even Quantity of Sales

A company has fixed operating costs of $5,000 and fixed financing costs of $10,000. The price per unit for one of its products is $12.00, and its variable cost per unit is $5.00.

Calculate the break-even quantity of sales.

Solution

$$ \text {Breakeven quantity of sales} =\cfrac {$5,000+$10,000}{($12.00-$5.00)} = 2,143 $$

3. Scenario Analysis

Sensitivity analysis, seen previously, does not allow us to see the interrelationships between the different project inputs. It only allows us to test the impact of a change in a single variable, one at a time, on the overall expected future outcomes of a project.

Scenario analysis, on the other hand, is a technique that allows us to consider the impact of changes in more than one input variable on the expected project outcome. This involves choosing particular scenarios or combinations of factors that a project may be exposed to, such as: a loss of funding, loss of a supplier, a natural disaster.

These combinations are then modeled and explored to assess the resulting impact on the profitability of a project

Scenario analysis is vital in deciding to find the best course of action to maximize the returns from a portfolio, that is, determining the best-case scenario and trying to avoid the worst-case scenario.

4. Monte Carlo Simulation

Monte Carlo simulation is a computer-generated sensitivity or scenario analysis that is based on probability models for the factors which drive outcomes. When doing simulations, each event or possible outcome is assigned a probability after which multiple scenarios are run using probability factors assigned to the possible values of a variable.

Monte Carlo simulation involves the creation of a computer-based model into which the variabilities and interrelationships between random variables are entered. A spread of results is obtained when the model is run many times – hundreds or thousands of times. The method is beneficial when the number of random variables is too high making the analysis using ordinary methods very complex.

In finance, we use Monte Carlo simulations to define potential risk. As an example, a mutual fund manager may use the method to manage assets and liabilities to try and establish any downward risk – the risk that liabilities will outgrow the assets leading to a loss.

The method can also be used in project appraisal, where the project manager tries to establish the financial viability of a project.

In most cases, there is usually an initial cash outlay followed by subsequent costs during the project’s productive life. The project also generates profit at specified times during the life of the project. If the present value of profit outweighs that of costs, the project is considered financially feasible.

Both profits and costs are likely to be affected by numerous underlying variables which may include interest rate movements, exchange rate fluctuations, technological changes, labor supply costs among others.

Monte Carlo simulation is able to incorporate all the variables into a model that can be iterated to highlight all the possible future outcomes of the project. The outcomes are then summarized in terms of probabilities. The least likely outcome and the most likely one can then be deduced.

Monte Carlo simulation comes with the advantage of incorporating a wider variety of scenarios in a single run.

It is, however, more expensive relative to other methods of risk analysis and may require the acquisition of an expert’s services.

Decision Trees Modeling

Decision tree modeling is a technique for decision-making in project analysis where much complex information needs to be considered. It is used in various fields, such as financial modeling. It provides a useful structure in which alternative decisions and their consequences can be laid down and evaluated.

They also help form an accurate and balanced picture of the risks and rewards resulting from a particular decision, such as choosing an appropriate portfolio.

A good example is the binomial option pricing decision tree analysis discussed in a later chapter.

Decision trees involve an individual making a decision based on the anticipated outcomes of each competing ventures. In this case, outcomes might be a return from a portfolio associated with a certain probability because each decision’s impact is known with certainty.

So, the choice of the favorable decision and its outcome is calculated by multiplying the outcome’s value and the corresponding probability.

Example: Decision Trees

Allan is the financial manager of a textile factory.  His factory has been successful in the last three years.  The manager wants to determine whether it is good to advise the management to expand the factory this year.

The cost of expanding the factory is $500. If he does nothing and the economy becomes favorable, and customers continue to buy lots of the factory’s products, he expects $3000 in revenue, while only $1000 if the economy is unfavorable. If the management agrees to expand the factory, the anticipated revenue will be $6,000 if the economy is favorable and $2000 if the economy is unfavorable.

Draw the decision tree to demonstrate the decision choices of the manager.

Solution

$$ \begin{array} {} & {} & {\scriptsize 0.4 } & \begin{matrix} \text {Favorable economy } (40\%) \\ \text {Profit} = $6,000 \end{matrix} \\ {} & \begin{matrix} \text { Expanding factory} \\ \text {Cost} = $500 \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {T=0} \begin{matrix} & { } & \\ &\Huge \nearrow & \\ &\Huge \searrow & \\ & { } & \end{matrix} & {} & \begin{matrix} {\scriptsize 0.6 } \\ \\ {\scriptsize 0.4 } \end{matrix} & \begin{matrix} \begin{matrix} \text {Unfavorable economy } (60\%) \\ \text {Profit} = $2,000 \end{matrix} \\ \\ \begin{matrix} \text {Favorable economy } (40\%) \\ \text {Profit} = $3,000 \end{matrix} \end{matrix} \\ {} & \begin{matrix} \text {Not expanding factory} \\ \text {Cost} = $0 \end{matrix} & {\Huge \begin{matrix} \nearrow \\ \searrow \end{matrix} } & {} \\ {} & {} & {\scriptsize 0.6 } & \begin{matrix} \text {Unfavorable economy } (60\%) \\ \text {Profit} = $1,000 \end{matrix} \\ \end{array} $$

We need to find the value of each outcome(Net Present Value) in the decision tree.

$$ \begin{align*} & NPV_{\text{Expanding}} = 0.4(6,000) +0 .6(2,000) – 500 = $3,100 \\ & NPV_{\text{No Expanding}} = 0.4(3,000) + 0.6(1,000) = $1,800 \\ \end{align*} $$

Since \($3,100 > $1,800\), the financial analyst should advise the management to expand the factory.

You will meet this kind of decision tree in binomial options pricing models in the later chapter, in which we will also discount each node using an interest rate.