Mean-Variance Portfolio Theory
After completing this reading, you should be able to: Explain the mathematics and... Read More
After completing this reading, you should be able to:
- Describe the characteristics and terms of the main derivative instruments (including forwards and futures).
- Distinguish between long and short positions for both assets (including short selling of stocks) and derivatives on assets.
- Recognize the transaction costs affecting profit calculations for both assets and derivatives on assets (including commissions and bid-ask spread)
- Describe the characteristics and terms relating to both forward contracts and prepaid forward contracts
- Define and recognize the following terms relating to the timing of stock purchases, outright purchases, fully leveraged purchase, prepaid forward contract, and forward contract.
- Determine payoffs and profits for both long and short positions on forward contracts
- Calculate the prices for both forward contracts and prepaid contracts on stocks with no dividends, continuous dividends, and discrete dividends
- Construct a synthetic forward from the underlying stock and a risk-free asset and identify arbitrage opportunities when the synthetic forward price is different from the market forward price
- Describe the characteristics and terms relating to both futures contracts and the associated margin accounts
- Define and recognize the following terms relating to the mark to market process; Marking to market, margin balance, maintenance margin, and margin call
- Evaluate investors margin balance based on changes in asset values
A derivative is a financial instrument whose value is derived from some underlying asset. It represents a legal agreement to trade a specific asset at a given future date for a particular price.
Common derivative instruments include futures and forward contracts.
A futures contract is a standardized, legally-binding agreement between two parties that specifies the price at which to trade a given asset (commodity or financial instrument) at a specified future date.
Futures contracts are traded on exchanges.
A forward contract is a non-standardized contract between two parties that specifies the price and the quantity of an asset to be delivered in the future. Forwards are non-standardized, meaning they cannot be traded on exchanges. Instead, they are traded in over-the-counter (OTC) markets.
Futures contracts differ from forwards in several ways as follows:
$$\small{\begin{array}{|l|l|}\hline
\textbf{Futures} & \textbf{Forwards} \\ \hline
\text{Traded on exchanges} & \text{Traded over the counter} \\ \hline
{\text{Standardized, i.e., choice of }\\ \text{expiry and size of trade limited}} & {\text{Not standardized, i.e.,}\\ \text{quality, price and maturity subject to}\\ \text{negotiation between the buyer and the seller}} \\ \hline
{\text{Three parties involved:}\\ \text{the buyer, the seller,}\\ \text{and the clearinghouse}} & {\text{Two parties involved:}\\ \text{the buyer and the seller}} \\ \hline
{\text{Parties obligated to trade;}\\ \text{thus, little or no counterparty risk}} & {\text{Parties can opt-out of the agreement;}\\ \text{thus, high counterparty risk}}\\ \hline
{\text{Marked to market and thus entail}\\ \text{daily settlements of margin payments}} & {\text{Payment only made once,}\\ \text{at the maturity of the contract}}\\ \hline \end{array}}$$
Long Position: When a party agrees to buy a specified underlying asset for a specified price on a given future date, they are said to be in a long position. This is because the party will have more of the underlying asset once the contract is settled.
Short Position: When a party agrees to sell a specified underlying asset for a specified price on a given future date, the party is said to be in a short position. This because the party will have less of the asset once the contract is settled.
Short selling involves the sale of a security which the investor does not own. The investor borrows the owner’s security, the lender, with a promise to return it at a specified date.
The short seller has reason to believe that the security is overpriced, or some other factors make it highly likely that the security will lose value shortly. Its goal, therefore, is to sell high and buy low and get to keep the difference (profit).
 When the short sale is closed out, the short seller must return the security to the lender. The lender may also request to have the asset even before closeout, depending on the initial agreement. There is always the risk that the security’s price will rise, forcing the investor to reacquire it at a higher price and thus make a loss.
When the short sale is closed out, the short seller must return the security to the lender. The lender may also request to have the asset even before closeout, depending on the initial agreement. There is always the risk that the security’s price will rise, forcing the investor to reacquire it at a higher price and thus make a loss.
Short sales are transacted through a broker. The short seller must deposit some collateral to guarantee the eventual return of the security to the owner. Also, the short seller is required to pay all accrued dividends to the lender. Thus, the net profit is equal to:
$$\text{Net profit}=\text{Sale price}-\text{Borrowing price}-\text{Divdident p aid}$$
These are costs incurred by investors for holding the long or short positions in futures and forward contracts.
These costs include storage costs, interest on loans used to make the investments, convenience yields, commissions, etc.
A forward contract on consumption assets such as on several tonnes of corn may have warehouse costs.
If the storage cost is a fixed cost \(U\) that is independent of the value of the underlying asset, then:
$$F_0=\left(S_0+U\right)e^{rT}$$
If the storage cost is a percentage of the underlying asset (yield), then:
$$F_0=S_0e^{\left(r+u\right)T}$$
This the additional value of holding the asset rather than having a long forward or futures contract on the asset.
An example of a consumption asset that has a convenience yield is oil. If you hold oil, you will have the convenience of selling it at a higher price during a shortage or using it to put it into your car. On the other hand, if you only had forwards or futures contracts for oil, you wouldn’t have the convenience of putting it into your car!
If a forward contract has a storage cost, expressed as a percentage of the underlying, as well as a convenience yield, then:
$$F_0=S_0e^{\left(r+u-y\right)T}$$
The carrying costs may lead the futures price to be slightly higher than the current spot price of the underlying asset in the market.
The bid-ask spread is the amount by which the ask price exceeds the bid price. The ask price represents the lowest price a seller is willing to sell the asset for, while the bid price will represents the highest price a buyer is willing to pay for the asset.
This is a method of paying for an asset in full with one payment. When you buy a stock outrightly, you own it immediately.
This is where an investor borrows the full amount to purchase an asset. It implies that the investor does not wish to invest his or her money in a risky asset. For instance, assume that an investor borrows \(S_0\) at a risk-free rate and then purchases an asset at the price of \(S_0\). At the maturity date of the loan, the investor pays \(S_{FV\left(0,\ T\right)}\) and now the value of the contract is \(S(T)\) so that the payoff of the contract is:
$$S\left(T\right)-S_{FV\left(0,\ T\right)}$$
We say that it is fully leveraged since the initial cost to purchase the asset is zero. However, the profits from an outright purchase and fully leveraged cost must be equal to avoid arbitrage opportunity from arising.
This a type of agreement where you pay the prepaid forward amount today to receive an asset on maturity or delivery date. Denote the prepaid price by then the payoff from the contract is:
$$S\left(T\right)-F_{FV\left(0,\ T\right)}^p$$
Payoffs refer to the difference between the forward price \(F\) agreed at time 0 and security price \(S_T\) at time \(T\).
The buyer of the underlying in a forward contract is said to be in a long position.
The payoff to long forward is:
$$S_T-F$$
The seller of the underlying is said to be in a short position.
The payoff to a short forward is:
$$F-S_T$$
The standard forward contract is set up so that there is no payment by any party at the contract’s onset.
Thus, the forward contract has no value at the onset of the contract. For a standard contract, the long forward payoff is 0 at the beginning of the contract.
If \(F_0\) is the agreed forward price at time 0, \(S_0\) the spot price at time 0, \(r\) the risk-free continuously compounded rate of interest applicable over the term of the contract and \(T\) the time to maturity, then:
$$F_0=S_0e^{rT}$$
This is known as the forward-spot parity relationship, and we will use this to compute the forward price in the next few sections
A farmer has entered into a three-month forward contract to sell 100 tons of wheat to a miller for $185. Three months later, when delivering the contract, a ton of wheat trades in the market for $190.
Calculate the farmer’s payoff should the contract be exercised.
The farmer is in a short position; thus, the payoff on expiry will be:
$$100\left(185-190\right)=-500$$
Forwards and futures are based on some specified underlying assets. The underlying assets may be either investment assets or consumption assets.
An investment asset is an asset held to invest. The holder takes a position in the asset in the hope of earning an income or capital gain. Examples include stocks and bonds issued by various financial institutions.
A consumption asset is an asset primarily held for consumption, and not for investment or resale. Examples include oil, coffee, tea, corn, etc.
The spot price is the current market price at which an instrument or commodity is bought or sold for immediate payment and delivery.
If we assume that:
Then, the relationship between spot prices and forward prices can be expressed as follows:
$$F_0=S_0e^{rT}\ldots\ldots\ldots\ldots.(i)$$
Where:
\(F_0\) = Forward price at present that is \(t=0\)
\(S_0\) = Underlying asset (spot) price today
\(r\) = Continuously compounded risk-free rate
\(T\) = Time to maturity of the forward contract in years
The forward price (left side of \(Eq. (i)\)) must equal the right side, i.e., the cost of borrowing funds to buy the underlying asset and carrying it forward to time \(T\).
If \(F_0 < S_0e^{rT}\), an arbitrageur can make a risk-free profit by selling the asset, lending out the proceeds, and buying the forward.
If \(F_0 > S_0e^{rT}\), an arbitrageur can make a risk-free profit by selling the forward and buying the asset with borrowed funds.
The current price of a 6-month zero-coupon bond is $79.2 per $100 nominal. The yield on the comparative 6-month government bond is 8%.
Calculate the forward price.
The forward price is given as:
$$K=S_0e^{rT}=79.2\times e^{0.08\times\frac{6}{12}}=$ 82.43$$
Carrying costs are any cash flows associated with the underlying asset over the life of the forward contract. The owner of the forward contract does not receive any of these cash flows, and therefore, their present value, call it, must be deducted from the spot price when determining the forward price. Thus,
$$F_0=\left(S_0-P\right)e^{rT}$$
If the cash flows are in the form of dividends paid at a continuously compounded rate \(q\), then:
$$F_0=S_0e^{\left(r-q\right)T}$$
If the dividends are paid discretely, then:
$$F_0=S_0e^{rT}-\sum_{i=1}^{n}{D_ie^{r\left(T-t_i\right)} }$$
Where,
Dividends are of the amount \(D_1,\ldots,\ D_i,\ldots,\ D_n\) at times \(0 < t_1 < \ldots < t_i < t_n \le T\).
An investor has entered into a one-year forward contract to purchase a given holding of a fixed interest corporate bond. The bond pays a coupon in 6 months at a 6% rate per $100 nominal and currently trades in the market for $93.
You are given that the constant risk-free force of interest is 5%.
Calculate the forward price.
The forward price of a stock with a fixed income is given by:
$$K=S_0e^{rT}-De^{r(T-t_1)}$$
Substituting the formula for values, we get:
$$K=93e^{0.05}-6e^{0.05\times0.5}=$91.62$$
An investor has entered into a forward contract to purchase a dividend-paying stock in 3 years’ time. The stock currently has a market price of $120 and pays dividends continuously. The current dividend is $3 per annum.
You are given that the risk-free force of interest is 4%.
Calculate the forward price.
The forward price is given by:
$$F_0=S_0e^{\left(r-q\right)T}$$
Where \(r\) is the risk-free constant force of interest, \(q\) the dividend yield, and \(T\) the term of the contract.
Given the market price of the stock and the dividend, the dividend yield is computed as
$$q=\frac{3}{120}=2.5\%$$
The forward price \(F_0\) is thus;
$$F_0=120e^{\left(4\%-2.5\%\right)3}=$125.52$$
A forward contract’s value can be defined as the difference between the spot price and the present value of the forward price.
Let \(K_0\) represent the forward price at time \(t=0\) for a forward contract to be delivered at time \(T\) and \(K_r\) the forward price at time \(r\) where 0<r<T
Also, let \(V_s\) and \(V_l\) represent the value of a short and long forward at time r, respectively and \(\alpha\) the risk free rate of return, then:
$$V_s=(K_0-K_r)e^{\alpha(T-r)}$$
The above formulas give the value to the seller (i.e., the party in a short position). By convention, the value to the buyer is obtained by taking a negative of the short position.
$$V_l=-V_s$$
The formula applies to all three cases: asset with no income, asset with fixed income and an asset with continuous income
An investor has entered into a forward contract on 1 January 2015 to purchase a given asset in 5 years’ time for $455. The current market price of a unit of the asset is $420. On 1 July 2018, the asset had a price of $435.
You are given that the forwards market is a perfect market with no arbitrage opportunities and that a constant risk-free force of interest applies over the term of the contract.
Calculate the value of the long forward contract on 1 July 2018.
We first compute the constant risk-free force of interest. We know that:
$$K_0=S_0e^{\delta T}$$
Thus,
$$455=420e^{5\delta} \Rightarrow \delta=1.6\%$$
Let \(K_r\) represent the price of a forward contract set up on 1 July 2018 with a term of 1.5 years. Then.
$$K_r=435e^{1.6\%\times1.5}=$445.57$$
The value of the forward contract is thus:
$$\left(445.57-455\right)e^{-1.5\times1.6\%}=-$8.618$$
An investor has entered into a forward contract to sell a dividend-paying stock in five years’ time. The stock has a current dividend yield of 5% and has just paid a dividend of $7.5. Two years into the contract, the stock price rises to $160.
The applicable risk-free force of interest over the term of the contract is 8%.
Calculate the value of the short forward two years into the contract.
First, calculate the current price of the stock.
$$\text{Divided yield}=\frac{\text{Dividend}}{\text{Current Price}}$$
Thus,
$$\text{Curennt price}=\frac{7.5}{0.05}=$150$$
The investor has agreed to sell. Therefore, we estimate his value in the short position.
Let \(K_0\) and \(K_2\) represent the forward price at time 0 and time 2, respectively.
$$K_0=150e^{\left(0.08-0.05\right)\times5}=$174.28$$
$$ K_2=160e^{\left(0.08-0.05\right)\times3}=$175.07$$
$$V_s=\left(174.28-175.07\right)e^{-0.08\times3}=-$0.62$$
You can offset the risk of a forward contract by constructing a synthetic forward to offset a position in the actual forward contract.
To see this, assume that the continuous dividends yield rate \(d\) and the risk-free of interest be \(r\). Now recall that the payoff of a long forward is \(S_T-F_0\).
Now assume that you borrow \(S_0e^{-dt}\) to buy \(e^{-dt}\) shares of the index to generate the payoff of \(S_T-F_{0,T}\).
Consider the following table:
$$
\begin{array}{l|l|l} \textbf{Transaction} & \textbf{Time 0} & \textbf{Time T (Expiration Date)} \\ \hline
\text{Purchase } e^{-dt} \text{ units of the index} & {-S}_0e^{-dt} & {+S}_T \\ \hline
\text{Borrow } S_0e^{-dt} & S_0e^{-dt} & {-S}_0e^{(r-d)t} \\ \hline
\text{Total} & 0 & S_T -S_0e^{(r-d)t} \\
\end{array}
$$
From the table above, the total payoff is equal to the forward payoff. Construction of synthetic forwards is mainly done to take advantage of arbitrage opportunities.
We now know that for a non-dividend-paying stock:
$$F_0=S_0e^{rt}$$
Hence,
If \(F_0<S_0e^{rT}\), an arbitrageur can make a risk-free profit by selling the asset, lending out the proceeds, and buying the forward.
If \(F_0>S_0e^{rT}\), an arbitrageur can make a risk-free profit by selling the forward and buying the asset with borrowed funds.
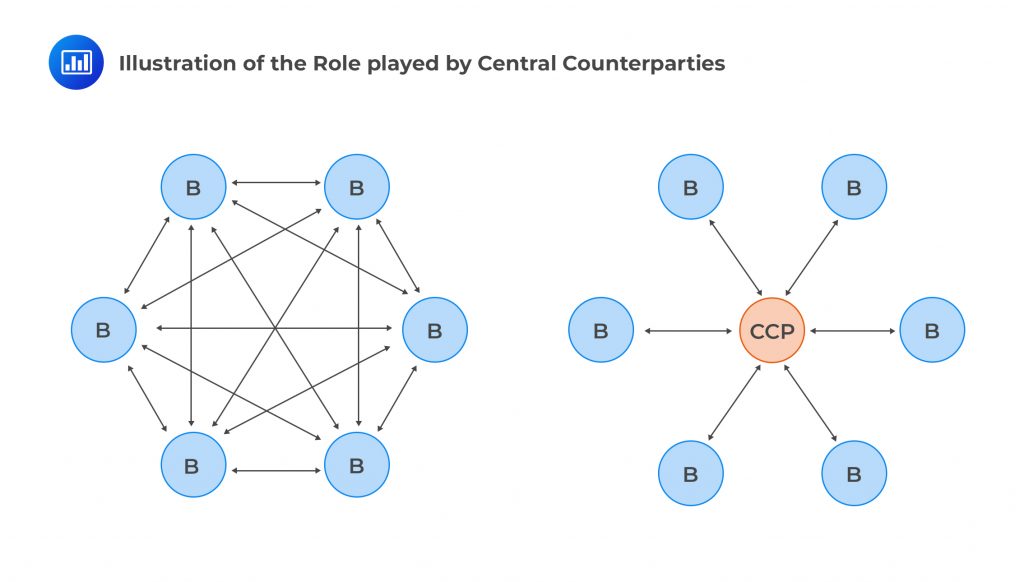
Futures contracts are traded through the clearinghouse. The clearinghouse is an interposed party between the buyer and the seller, ensuring the contract’s performance.
The clearinghouse acts as a counterparty between the buyer and the seller of the option guaranteeing each party security against credit risk and default. In essence, it acts as if it has sold to the buyer and bought from the seller removing the one on one interaction between the buyer and the seller.
The following view, although a bit simplistic, helps to show the role played by clearing houses (also called central counterparties or CCPs in over-the-counter markets):
 Margin
MarginIn exchange for this security, the futures contract parties are required to deposit a specified amount with the clearinghouse. This amount is known as a margin and is used to shoulder against potential losses; the parties may suffer due to price movements over the term of the contract.
Two types of Margins are required
Suppose that Mr. Donald has entered into a futures contract to purchase a given holding of fixed interest security in 6 months’ time from Mr. Brolin for $75 per $100 nominal.
The clearinghouse will, for example, demand that both Brolin and Donald deposit a refundable $10 to their accounts. This is known as the initial margin.
Over the term of the contract, the price of the underlying security may change. If the price falls to say $70, Mr. Brolin will more likely be happy and willing to honor the agreement as the price movement favors him.
On the other hand, Mr. Donald will be more likely to default as the price movement has been to his disadvantage as he will have to pay $75 for a security that is only worth $70.
However, because each party had deposited the initial margin of $10 at the start, the clearinghouse will deduct $5 from Mr. Donald’s account to balance the deficit and pay $5 to Mr. Brolin.
Suppose that the maintenance margin was set at 30% of the initial margin, and the underlying security prices further fell to $66. The clearinghouse will deduct a further $4 from Mr. Donald’s account to balance the deficit and leave his margin account with a balance of $1.
Because Mr. Donald’s margin account balance is below the maintenance margin level of $3, the clearinghouse will prompt Mr. Donald to deposit $9 to bring his margin account back to the initial margin level of $10.
When an investor’s margin balance falls below the maintenance margin, the clearinghouse will prompt the investor to deposit the deficit. This is referred to as a margin call.
Note: If the price rises on any given day, the long investor will profit, and the short will make a loss. Margin calls will always be made to the party that has made a loss, provided the maintenance margin is breached.
The daily settlement of gains and losses on the contracts by the clearing house is called marking to market.
Marking to market avoids the accumulation of large losses over time that would otherwise lead to a default by the party in the loss-making position.
Consider an investor who enters in a long gold futures contract at $300. Each contract is worth 100 trounces (with a market value of $30,000). The initial margin required is $5,000, while the maintenance margin is $3,000.
Day 0: Margin account balance = $5,000
Day 1: The price moves to $290. Hence, the investor makes a loss of $1,000(=$10×100). The ending balance of the margin account is now $4,000. Since this is above the maintenance of $3,000, no funds need to be added to the account, i.e., no margin call.
Day 2: The price moves further down to $278. The investor thus makes a further loss of $1,200(=$12×100). This leaves the margin account with just $2,800(= $ 4,000−$1,200). That is below the maintenance margin. Therefore, the investor will receive a margin call requiring it to deposit some $2,200 into the margin account to bring it up to the initial margin required. This amount (needed to bring the account back to the initial margin) is called the variation margin.
An investor enters into a short position in a coffee futures contract at $500. Each futures contract controls 100 bags. The initial margin is $10,200, and the maintenance margin is $9,100.
Determine the amount of variation margin required at the close of business on the second day.
A short will make a profit if the price of the instrument goes down. Conversely, they will make a loss if the price of the underlying rises.
Day 0: Margin account balance = $10,200
Day 1: The price moves up to $510. Hence, the investor makes a loss of $1,000(=$10×100). The ending balance of the margin account is now $9,200. Since this is above the maintenance of $9,100, no funds need to be added to the account, i.e., no margin call.
Day 2: The price moves further up to $517. The investor thus makes a further loss of $700(=$7×100). This leaves the margin account with just $8,500(= $ 9,200−$700). That is below the maintenance margin. Therefore, the investor will receive a margin call requiring them to deposit some $1,700 into the margin account to bring it up to the initial margin required.