General Properties of Options

After completing this reading, you should be able to:

1. Explain the cash flow characteristics and terms relating to various options

• • Define and recognize the following terms relating to option classification: call and put options, expiration date, strike price, moneyness, and option style.
  • Calculate the payoff and profit on both long and short positions with respect to both call and put options.
  • Calculate the payoffs on exotic options: Asian (Arithmetic and Geometric), barrier, compound, gap, and exchange.
  • Calculate the payoffs on exotic options, lookback, chooser, shout, rainbow, and forward start.

2. Apply option strategies in a risk management context

• • Recognize that a long put can be used as an insurance strategy for a long stock position, and a long call can be used as an insurance strategy for a short stock position.
  • Understand how the following option strategies can be used as tools to manage financial risk or speculate on price or volatility: option spreads (bull, bear, ratio), collar, straddle, strangle, and butterfly spread.
  • Evaluate the payoff and profit of the option strategies described above.

1. 3. Explain the general properties of options that affect option prices.

• • Apply put-call parity to European options on stocks with no dividends, stocks with continuous dividends, stock with discrete dividends, currencies, and bonds.
  • Compare options with respect to term to maturity and strike price.
  • Identify factors affecting the early exercise of American options and the situations where the values of European and American options are the same.

Cash Flow Characteristics and Terms Relating to Various Options

Definition of Options

An options contract is an agreement between two parties to trade an underlying security at a predetermined price called the strike price on or before a specified future date called the expiration/maturity date.

An option gives the holder the right but not the obligation to buy/sell the underlying asset at an agreed-upon future date at the strike price.

Types of Options

Two types of options exist

1. Call Option: Gives the holder the right but not obligation to buy the underlying asset at the strike price on a specified future date.
2. Put Option: Gives the holder the right but not obligation to sell the underlying asset at the strike price on a specified future date.

Terms Relating to Options Classification

Strike Price

An option is enforced when the holder buys or sells the specified underlying asset on the agreed date. The price at which the holder buys or sells the underlying asset is known as the strike price or exercise price.

Exercise Date

This is the date upon which the holder buys or sells the underlying asset. It is the date when the contract is actually exercised. 

Expiration Date

This refers to the last date upon which the option contract can be traded. Beyond this date, the contract becomes invalid and worthless.

For European options, this date is the same as the exercise date.

For an American-style option, the expiration date may be different from the exercise date. American style options allow the holders to exercise the option on any date before and up to the expiry date.

Moneyness

Moneyness of an option refers to the payoff the holder stands to gain or lose if the option was to expire today.

It is based on the intrinsic value of an option, which is derived from the difference between the prevailing market price of the underlying asset and the strike price. The difference between the intrinsic value and the option premium is known as the time value of an option.

The following three terms are used to describe the payoff position:

1. At the money: When the option’s strike price is the same as the market price of the security on a given date, the option is said to be at the money. The payoff from the option is, therefore, zero.
2. In the money: When an option has a positive intrinsic value, then it is said to be in the money. For a holder of a call, this is when the underlying asset’s market price is higher than the strike price. For a holder of a put, this is when the market price of the underlying asset is lower than the strike price
3. Out of the money: When the payoff from enforcing the option’s right is negative, the option is said to be out of the money. This is when the underlying asset’s price is lower than the strike price for a call holder. For a put holder, this is when the underlying asset’s price is higher than the strike price.

Graphically, the moneyness of a call option with a strike price of USD 150 can be represented as the following:

Option holders will only exercise their rights to buy or sell if they stand to benefit from the transaction. They would therefore not exercise an out-of-the-money option.

Option Style

Option style defines an option’s characteristics based on the dates upon which these options can be exercised.

Two common styles exist:

1. American style: This allows the holders to exercise the option on any date before or on the expiry date.
2. European style: Holders can only exercise their rights to buy or sell on the expiry date.

Payoff and Profit on Options

Options give the holder the right but not the obligation to trade the specified underlying asset at the strike price on maturity.

Therefore, an investor would only exercise their right to buy or sell the underlying asset if they stand to benefit from the deal.

To shoulder the writer from the possibility of default from the holders, options are sold at a price. This price is known as the option premium, and it represents the writer’s payoff should the holder choose not to exercise the option.

Long Call Option-Payoff and Profit

An investor who purchases a call option is said to be in a long position.

Let \(S_T\) denote the security price on the maturity date, \(X\) the strike price of the option, \(C_0\) the option premium, and \(C_T\) the option payoff.

At maturity, the holder would exercise their right if \(S_T>X\). Otherwise, they would walk away from the deal and lose the option premium. The payoff to the investor would thus be:

$$\begin{align}\text{Payoff}&=\begin{cases}S_T-X, &\text{if}\ S_T > X\\0, &\text{if}\ S_T\leq X\\ \end{cases}\\ &=\text{max}\left(0,S_T-X\right)\end{align}$$

And the profit can be represented as:

$$\begin{align}\text{Profit}&=\text{Payoff}-\text{Option Premium}\\ &=max(0,S_T-X)-C_0\end{align}$$

Graphically, the profit of a long call option will be represented as the following:

Short Call Option-Profit and Payoff

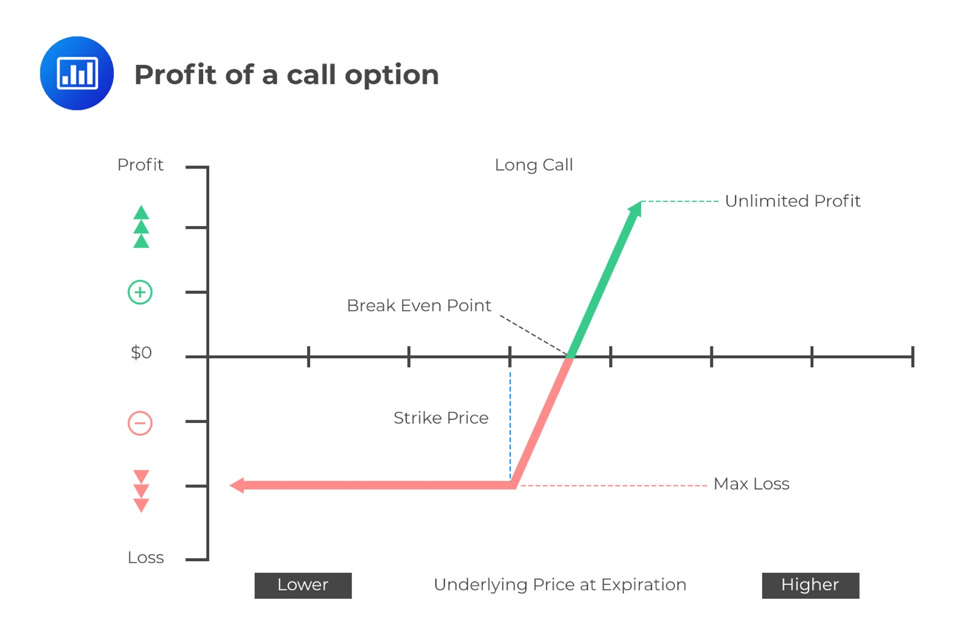
The writer of a call option is said to be in a short position. If the option is exercised, the payoff to the short position will be:

$$\begin{align}\text{Payoff}&=\begin{cases}-\left(S_T-X\right), &\text{if}\ S_T > X\\0, &\text{if}\ S_T\leq X\\ \end{cases}\\ &=-\text{max}\left(0,S_T-X\right)\end{align}$$

The payoff to the short call is just the opposite of the payoff to the long call position.

And the profit can be represented as:

$$\begin{align}\text{Profit}&=\text{Payoff}+\text{Option Premium}\\ &=-max(0,S_T-X)+C_0\end{align}$$

Graphically, the profit of a short call option will be represented as the following:

Example: Call Option Payoff and Profit to the Long and Short Positions

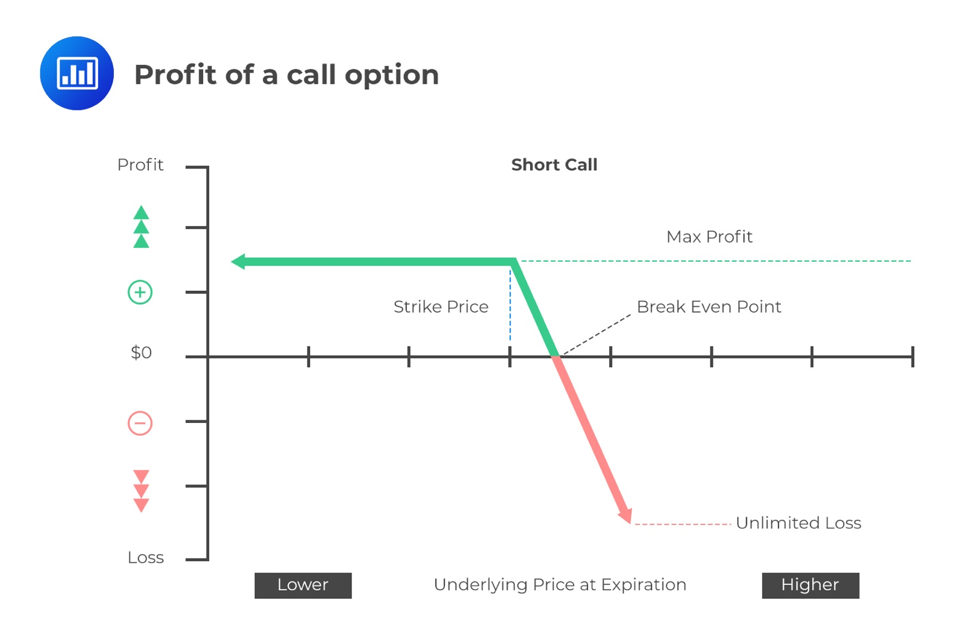
An investor has purchased a 6-month call option on the Nasdaq 500 with a strike price of $120. On maturity, the price of the Nasdaq 500 was $123. The investor paid the writer $1.50 for this option.

Calculate the payoff and profit to the investor and the short position. (Ignore interest on the premium)

Solution

The security price is greater than the strike price on maturity. The investor who is in a long position will thus exercise the option, and the payoff will be:

$$\begin{align}\text{Payoff}&=\text{max}\left({0,S}_T-X\right)\\ &=\text{max}(0,$123-120)=\$\ 3\end{align}$$

The profit to the long if the call is exercised is given as the difference between the payoff and the cost of setting up the contract (the option premium):

$$\text{Profit}=max[0, \$\ 123-\$\ 120 ]-\$\ 1.5$$

Since the option is exercised, the payoff to the short will be:

$$\text{Payoff}=-\text{max}\left(0,\$\ 120-\$\ 123\right)$$

So that:

$$Profit=-\text{max}\left[\left(0,\$\ 120-\$\ 123\right)\right]+\$\ 1.5=-\$\ 1.5$$

Long Put Option-Payoff and Profit

An investor who purchases a put option is said to be in a long position. Given that a put option gives the right but not the obligation to sell, the holder would only exercise their right if the security price is lower than the strike price on maturity.

The payoff will thus be:

$$\begin{align}\text{Payoff}&=\begin{cases}\left(X-S_T\right), &\text{if}\ S_T < X\\0, &\text{if}\ S_T\geq X\\ \end{cases}\\ &=\text{max}\left(0,X-S_T\right)\end{align}$$

Profit = Payoff – Option premium. That is:

$$\begin{align}\text{Profit}&=\text{Payoff}-\text{Option Premium}\\ &=max(0,X-S_T)-C_0\end{align}$$

Graphically, the profit of a long put option will be represented as the following:

Short Put Option

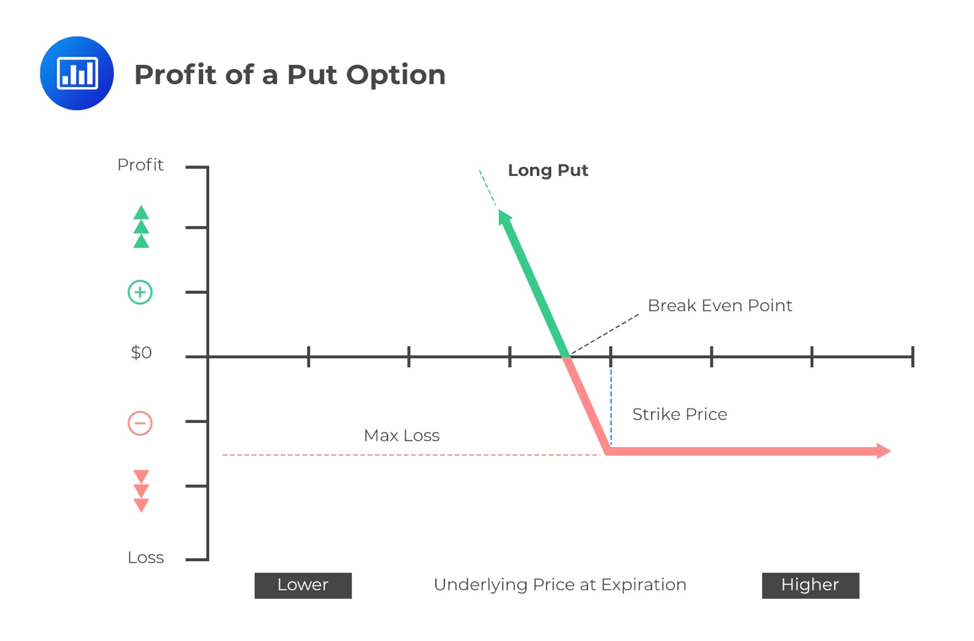
The writer of a put option is said to be in the short position. The payoffs for the writer are as follows:

$$\begin{align}\text{Payoff}&=\begin{cases}-\left(X-S_T\right), &\text{if}\ S_T < X\\0, &\text{if}\ S_T\geq X\\ \end{cases}\\ &=-\text{max}\left(0,X-S_T\right)\end{align}$$

Also,

$$\begin{align}\text{Profit}&=\text{Payoff}+\text{Option Premium}\\ &=-max(0,X-S_T)+C_0\end{align}$$

Example: Put Option Payoff to the Long and Short

Joe Cole has entered into a contract that gives him the right but not obligation to sell 100 shares of ABC limited to another investor in 6 months at a price of $4.50 per share. To lock in the contract, Joe has paid the investor $25 today. The continuously compounded risk-free rate of return is 2.5% p.a. applicable over the contract term.

In 6 months, the shares of ABC Limited are trading at a price of $4.30.

Calculate the payoff and profit to both Joe and the investor.

Solution

A put option gives the buyer the right but not the obligation to sell the specified underlying asset on maturity at the strike price.

The buyer, in this case, Joe will only exercise the put if the stock price is lower than the strike price on maturity.

Payoff to Joe

$$\begin{align}\text{Payoff}&=\max\left(X-S_T,0\right)\\ &=\max\left(\$\ 4.5-\$ 4.3,0\right)\times100=\$20\end{align}$$

Profit to Joe

$$\text{Profit}=\left[100\times\text{max}\left(\$\ 4.5-\$\ 4.3,0\right)\right]-\$\ 25e^{2.5\%\times 0.5}=-\$5.31$$

Thus even Joe obtains a positive payoff on the put. His overall profit is negative because the option premium is higher than the payoff from exercising the put

The payoff to the Investor

The investor is in a short position. His payoff will be:

$$100\times-\left[\max\left(\$4.5-\$4.3,0\right)\right]=-\$20$$

Profit to the investor

$$100\times-\left[\max\left((4.5-4.3,0\right))\right]+{25}^{0.025\times 0.5}=\$\ 5.31$$

The investor will obtain a positive profit because the accumulated premium plus interest is more than the payoff for the long.

Exotic Options

Exotic options are options that have non-standard characteristics and are only traded over the counter. They are typically sold by the investment banks and are set to meet a particular investor’s needs. Intuitively, due to their customization, they are rarely traded or rather not actively-traded, unlike other options.

Asian Options

In an Asian option, the payoff depends on the average price of the underlying asset over a period of time as opposed to standard options where the payoff is determined by the price of the underlying at a specific point in time.

Arithmetic Asian Options

The average can be calculated arithmetically as:

$$ \text{Arithmetic average}=\frac {s_1+s_2+ \cdots +s_n}{n} $$

While the payoff from the arithmetic Asian options is given by:

$$ \begin{align*} \text{Call Option} & =\text{max}\left[ 0,\left( \cfrac { 1 }{ n } \sum _{ i=1 }^{ n }{ { S }_{ i } } -K \right) \right] \\ \text{Put Option} & = \text{max}\left[ 0,K-\left( \cfrac { 1 }{ n } \sum _{ i=1 }^{ n }{ { S }_{ i } } \right) \right] \\ \end{align*} $$

Example: Arithmetic Average Asian Option

An investor has purchased a 6-month arithmetic average Asian call option on a portfolio of shares with a strike price of $67. The observed stock prices over the monthly time intervals are $55, $72, $66, $81, $62, and 78.

Calculate the payoff to the investor.

Solution

The payoff to the investor is given by:

$$\begin{align}\text{Payoff}&=\text{max}\left[ 0,\left( \cfrac { 1 }{ n } \sum _{ i=1 }^{ n }{ { S }_{ i } } -K \right) \right]\\ &=\text{max}\left(0,\frac{55+72+66+81+62+78}{6}-67\right)\\ &=\text{max}\left(0,69-67\right)=\$\ 2 \end{align}$$

Geometric Asian Options

The average can be calculated geometrically as:

$$ \sqrt [ n ]{ s_1 s_2 \cdots s_n } $$

The payoff from the geometric Asian options is given by:

$$ \begin{align*} \text{Call Option} & =\text{max}\left[ { \left( 0,\prod _{ i=1 }^{ n }{ { S }_{ i } } \right) }^{ \cfrac { 1 }{ n } }-K \right] \\ \text{Put Option} & =\text{max}\left[ 0,K-{ \left( 0,\prod _{ i=1 }^{ n }{ { S }_{ i } } \right) }^{ \cfrac { 1 }{ n } } \right] \\ \end{align*} $$

Example: Geometric Average Asian Option

An investor has purchased a 6-month geometric average Asian call option on a portfolio of shares with a strike price of $67. The observed stock prices over the monthly time intervals are $55, $72, $65, $81, $62, and 78.

Calculate the payoff to the investor.

Solution

The payoff for a geometric Asian option to the investor is given as:

$$\begin{align}\text{Call Option} & =\text{max}\left[  \left( 0,\prod _{ i=1 }^{ n }{ { S }_{ i } } \right)^{ \cfrac { 1 }{ n } }-K \right] \\ &=\text{max}\left(0,\left(55\times72\times66\times81\times62\times78\right)^\frac{1}{6}-67\right)\\&=\text{max}\left(0,68.397-67\right)=\$\ 1.397\end{align}$$

Barrier Options

A barrier option is an option whose existence depends upon the underlying asset’s price reaching a predetermined barrier level. It can be either:

• A knock-out, implying it expires worthless if the underlying exceeds a certain specified price, effectively limiting profits for the holder but limiting losses for the writer.
• A knock-in, implying it has no value until the underlying reaches a certain specified price.

Example: Barrier Option

Consider an up and out barrier call option with a strike price of $63 for an underlying asset with a barrier of $70. The asset currently trades in the market at $65. A long investor has paid a price of $3 to hold this option. During the lifetime of the option, the price of the underlying asset reaches $71.

Determine the payoff for a long call option holder.

Solution

The up and out option means that the option ceases to exist if the underlying asset’s price reaches a certain barrier. Given that the price of the underlying asset breached the barrier during the option’s lifetime, the option becomes worthless.

The long position (i.e., the holder) loses the premium paid ($3), and thus the payoff will be (0)

Compound options

A compound option is simply an option on an option, i.e., an option for which the underlying is another option. A compound option can take one of four different forms:

• A call on a call (CoC) gives the investor the right to buy a call option at a set price for a set period of time.
• A call on a put (CoP)gives the investor the right to buy a put option at a set price for a set period of time.
• A put on a call (PoC) gives the investor the right to sell a call option at a set price for a set period of time.
• A put on a put (PoP) gives the investor the right to sell a put option at a set price for a set period of time.

Given that a compound option is an option on an option, it will have two strike prices and exercise dates, one for the underlying option and the other for the compound option.

Suppose at time \(t_0\) we buy a call compound option, which gives us the right to purchase an underlying call option at time \(t\) which expires at time \(T\). Let \(X\) be the strike price of the compound and \(K\) be the strike price of the underlying call. Also, let \(S_t\) be the security price at time \(t\) when the investor exercises the compound call and \(S_T\) be the security price at time \(T\) when the underlying call matures.

The compound call option will only be exercised if at time \(t\) the security price \(S_t\) is greater than the compound option strike price, \(X\).

The payoff for the call on a call to an investor is thus given as:

$$\text{Payoff}=\text{max}[0,C\left(S_T,K,T-t\right)-X]$$

In the same way, we can write the payoff for the other compound options:

$$\begin{align}\text{Call on put} &=\text{Payoff}=\text{max}[0,P\left(S_T,K,T-t\right)-X]\\ \text{Put on call}&=\text{Payoff}=\text{max}[0,X-C\left(S_T,K,T-t\right)]\\ \text{Put on Put} &=\text{Payoff}=\text{max}[0,X-P\left(S_T,K,T-t\right)]\end{align}$$

Where \(C\) and \(P\) represent the price of the underlying call and put options, which can be computed using the Black-Scholes Option Pricing Model.

Gap Options

A gap option has a strike price, \(K_1\), and a trigger price, \(K_2\). The trigger price determines whether or not the option will have a nonzero payoff. The strike price determines the actual amount of the payoff.

For a gap call option, the payoff will always be nonzero (positive or negative) as long as the final stock price exceeds the trigger price. 

$$ \text{Gap call option payoff}=\begin{cases} \begin{matrix} { S }_{ T }-{ K }_{ 1 }\quad if\quad { S }_{ T }>{ K }_{ 2 } \end{matrix} \\ 0,\quad if\quad { S }_{ T }\le { K }_{ 2 } \end{cases} $$

If the trigger price is less than the strike price for a gap call option, negative payoffs are possible.

The payoff will always be non-zero for a gap put option as long as the final stock price is less than the trigger price.

$$ \text{Gap put option payoff}=\begin{cases} \begin{matrix} { { K }_{ 1 }-S }_{ T }\quad if\quad { S }_{ T }<{ K }_{ 2 } \end{matrix} \\ 0,\quad if\quad { S }_{ T }\ge { K }_{ 2 } \end{cases} $$

If the trigger price is greater than the strike price for a gap put option, negative payoffs could occur.

If \(K_1=K_2\), the gap option payoff will be the same as that of an ordinary option.

Example: Gap Put Option Payoff

The current market price of a security is $500. An investor has entered into a contract that will give him the right to sell this asset in 9 months for a price of $440 provided the price of the asset is less than $450. On maturity, asset trades in the market at a price of $430.The investor has paid a premium of $5 to buy this contract.

Calculate the payoff to the investor.

Solution

The trigger price is $450, and the asset price on maturity is $430. Because the investor is long on the contract, he will exercise his right. Thus, the payoff is given by:

$$\text{max}(440-430,0)=$10$$

Note: Payoff ignores the costs of setting up the contract (i.e., commissions, premiums, etc.)

We note that in this case, the trigger is higher than the strike price. Thus it is possible for the investor to have a negative payoff if the price of the underlying asset on maturity lies between $440 and $450

Such a case will usually result in the holder of the option to pay less premium for the contract because of the possibility of having a negative payoff.

For a gap call option, if the trigger price is less than the strike price, then a negative payoff to the holder would also be possible.

Exchange Options

An exchange option gives the right but not the obligation to exchange money denominated in one currency, say, the USD, into another currency, say, the Euro, at a pre-set exchange rate on a specified date.

Consider a European option to give up an asset worth \(X_T\) at time \(T\) and receive in exchange an asset worth \(Y_T\). The payoff from the option is simply:

$$ \text{max}⁡(X_T-Y_T,0) $$

Lookback Options

A lookback option is an option whose payoff at the expiration date depends on the maximum or the minimum value achieved by the option’s underlying asset during the option’s life.

There are two distinct types of lookback options

Floating Strike Lookback

The strike price is decided on maturity as the most favorable price of the underlying asset over the option’s life. Put simply, the strike price is allowed to vary over the contract term.

In this case, the payoff for a floating strike lookback call will be obtained from the current market price and the minimum possible price attained by the underlying over the option’s life as the strike price

$$\text{Payoff}=S_T-S_{min}$$

For a floating strike put, the payoff will be derived from the current market price and the maximum possible price attained by the underlying asset over the option’s life as the strike price.

$$\text{Payoff}=S_{max}-S_T$$

Fixed Strike Lookback

Here, the strike price is specified at the start of the contract. The payoff will thus be based on the minimum and maximum prices attained by the underlying asset over the term of the contract.

For a fixed strike call, the payoff will be computed as the maximum possible price attained by the underlying asset over the term of the contract minus the strike price 

$$\text{Fixed strike call payoff}=S_{max}-K$$

For a fixed strike put, the payoff will be computed as the strike price minus the minimum possible price attained by the underlying asset over the term of the contract

$$\text{Fixed strike put payoff}=K-S_{min}$$

Example: Lookback Option

An investor has purchased a put lookback option that gives him the right but not obligation to sell a specified underlying stock in 6-months at a strike price of $75 per share. The following are the share prices recorded at the end of each of the last 6 months: $58, $63, $71, $69, $72, and $74. The selected price is such that it is the maximum or minimum price over the term of the contract that gives the investor the best available payoff.

Calculate the payoff to the seller of this option.

Solution

The investor has purchased a put and would thus benefit if the minimum possible price is selected as the security price on maturity. The investor’s payoff is:

$$\text{max}(0,K-S_{min})=\text{max}(0,75-58)=17$$

The payoff to the short is the negative of the long position’s payoff.

The seller’s payoff will thus be:

$$-\text{max}\left(0,75-58\right)=-\$17$$

Chooser Options

This is a type of option that gives the buyer the right to choose after a predetermined period has elapsed, whether the option is a call or a put. The value of a chooser option at the time of the purchase should be higher than either a call or a put option.

The payoff from a simple chooser option is given by:

$$ \text{Payoff}=\text{max}⁡(C,P) $$

Where \(C\) and \(P\) denote the European call and put values of the underlying option respectively.

If the underlying call and put options are both European with the same time to expiry \(C\) and the strike price \(X\), the payoff at time \(t\) can be represented as follows assuming the put-call parity:

$$ \begin{align*} \text{Payoff} & =\text{max}⁡(C,P) \\ & =\text{max}\left( C,C+Xe^{-r(T-t) }-S_t e^{-q(T-t) } \right) \\ & =C+\text{ max }⁡\left( 0,Xe^{ -r(T-t) }-S_{ t }e^{ -q(T-t) } \right) \\ \end{align*} $$

Where:
\(S_t\) = share price at any time \(t\);
\(X\) = strike price;
\(t\) = the time at which the holder of the chooser decides whether the option will be a call or a put;
\(T\) = maturity of the option;
\(r\) = risk-free rate of return; and
\(q\) = dividend yield.

Example: Chooser Option

On 1 January 2019, Ben Davis paid $2 to purchase a 9-month contract that allows him to decide on 1 April 2019 whether the option is a call or a put. The exercise price agreed on 1 January 2019 was $55, and on 1 April 2019, the price of the underlying was $62 and thus elected to have a call option. The price of the underlying security on maturity was $58.

Calculate the payoff for Davis at the end of the contract.

Solution

The chooser period is before the maturity date. Davis selected to have a call option. Given that the underlying asset price is greater than the strike price on maturity, the option will be exercised. The payoff is therefore given by:

$$\text{Payoff}=\text{max}(0,$58-$53)=\$\ 5$$

Note on Chooser Options

If the chooser period is the same as the option maturity date, the simple chooser option will be equivalent to a straddle (which we will see later in this chapter). We can see this as follows:

Let \(T\) represent the maturity date and the chooser date. Also let, \(K\) be the strike price of the call and puts, and \(S_T \) be the price of the underlying at time \(T\). The payoff function for an investor would be:

$$\text{max}\left(C,P\right)=\text{max}\left[\max\left(S_T-K,0\right),\max\left(K-S_T,0\right)\right]=S_T-K$$

Shout Options

In a shout option, the holder can lock profits at defined intervals while maintaining the right to continue participating in gains without a loss of locked-in profits. When the purchaser exercises this right and the minimum payoff of the option is locked in, the buyer is said to “shout” these instructions to the option writer and hence the name.

As usual, let \(S_t\) be the value of the share for which the option is written,\(S^{\ast}\) be the value of the share when the buyer shouts to the writer and let \(K\) be the strike price and \(T\) denote the time expiration date. Then the payoff of the shout call option is as follows:

If the shout is exercised:

$$\text{max}(S_T-K,S^{\ast}-K,0)$$

If the shout is not exercised:

$$\text{max}(S_T-K,0)$$

For the case of the shout put option, the payoff is as follows:

If the shout is exercised:

$$\text{max}(K-S_T,K-S^{\ast},0)$$

If the shout is not exercised:

$$\text{max}(K-S_T,0)$$

From the above expressions, it is clear to see that if the shout option is not exercised, the payoffs are the same as that of standard put and call options.

Lastly, a shout call option allows the purchaser to lock in a one-time gain in the underlying share or any other asset while the shout put option allows the buyer to lock in a one-time loss in the underlying share. The shout call option will never be exercised if \(S_T \le K\), and the shout put option will never be exercised if \(S_T \ge K\).

For example, if the strike price of a call option is $75 but mid-way through the contract, the share trades at $80, the holder of a call option may exercise the shout and lock in the $5 profit. Additionally, the call option holder can still make additional profits if the prices of the underlying assets increase before expiry.

Say, for example, if at maturity the price of the underlying asset is $78, the investor will exercise the option and obtain a payoff of $5, i.e. the maximum of $5 and $3

Rainbow Option

This is a type of option whose value is dependent on two or more risky assets. Thus, the payoffs from a rainbow option are:

The payoff from the call on maximum asset value (in this case, share price):

$$  =\text{max}(\text{max}(S_1,S_2,…,S_m )-X,0). $$

The payoff from a call on minimum asset value (in this case, share price):

$$  =\text{max}(\text{min}(S_1,S_2,…,S_m )-X,0). $$

The payoff from put on maximum asset value (in this case, share price):

$$=\text{max}(X-\text{max}(S_1,S_2,…,S_m ),0).$$

The payoff from put on minimum asset value (in this, case share price):

$$  =\text{max}(X-\text{min}(S_1,S_2,…,S_m ),0). $$

The payoff from put B and call A:

$$ =\text{max}(S_A-S_B,0) $$

Example: Rainbow Call Option

An investor has entered into a contract that gives him the right but not obligation to buy the best of an asset from a portfolio of underlying government bonds at a strike price of $55. The writer has identified three bonds to deliver, and the bonds were trading at $49, $56, and $57.50 on maturity.

Calculate the payoff to the long investor from the call on maximum asset value.

Solution

The payoff from a call on maximum asset value is given as:

$$\begin{align}&=\text{max}[\text{max}\left(S_1,S_2,\ldots,S_m\right)-X,0] \\&=\text{max}{\left[\text{max}{\left(57.50,56,49\right)}-55,0\right]}=\$\ 2.50\end{align}$$

Forward Start Option

This is an option that is purchased and paid for now but becomes active later with a strike price determined at that time. The same basic principles as that standard options apply here, only that the timing is different.

Options Strategies in Risk Management

Use of a Long Put as an Insurance Strategy for a Long Stock Position

A long put, also known as a protective put, is a hedging strategy where the holder of security buys a put to protect themselves against a drop in that security’s stock price. This strategy is mostly employed, especially in insurance.

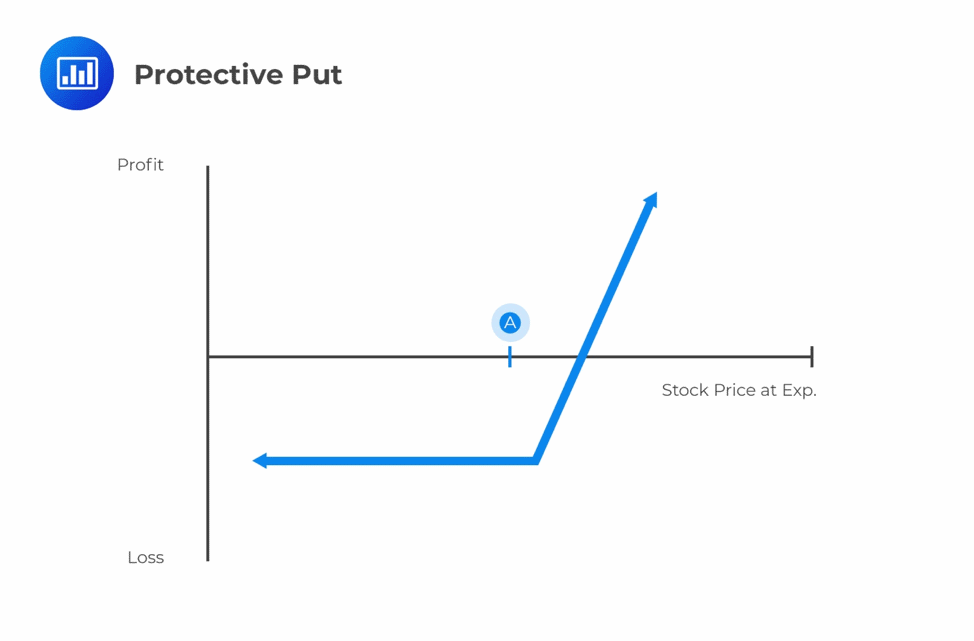For example, an investor may purchase a long put to sell the underlying asset at a strike price of $30. If the underlying asset price falls to say $20, the investor may still exercise his/her right and sell the underlying asset at $30. However, if the price of the underlying asset increases, to say $40, the investor will choose not to trade and only lose the premium paid.

A protective put has unlimited profit potential. A profit is achieved when the underlying stock price exceeds its purchase price, plus the premium paid for the option. On the other hand, the maximum loss is limited and is equal to the premium paid for buying the put option. In summary,

• Max profit = Unlimited
• Max Loss = Premium Paid + Purchase Price of Underlying – Put Strike + Commissions Paid

A protective put is taken by bullish investors worried about near-term uncertainties on a stock.

Use of a Long Call as an Insurance Strategy for a Short Stock Position

A long call is a strategy whereby an investor uses a call option in anticipation of an increase in the prices of the underlying asset.

The holder of a long call expects the price of the underlying asset to increase in the future. However, rather than holding the underlying asset, the investor purchases a call option on the underlying asset at a lower strike price.

If the security price increases, the investor exercises the right to buy at the lower price and resell at the market price to make a positive profit. However, if the security price falls, the investor chooses not to exercise the option and thus loses the premium paid for the call option.

Option strategies as tools to manage financial risk and their payoffs

Option Spreads

Spread strategies involve taking a position in two or more options of the same characteristics or type. That is two or more calls puts. They include:

Bull Spread

A bull spread is a bullish options strategy designed to take advantage of a moderate rise in the near term’s underlying asset price.

In a bull call spread, the bullish trader buys a call with a lower strike price and simultaneously sells a call with a higher strike price. The premium received from the sale of the higher strike call subsidizes the premium paid for the purchase of the lower strike call.

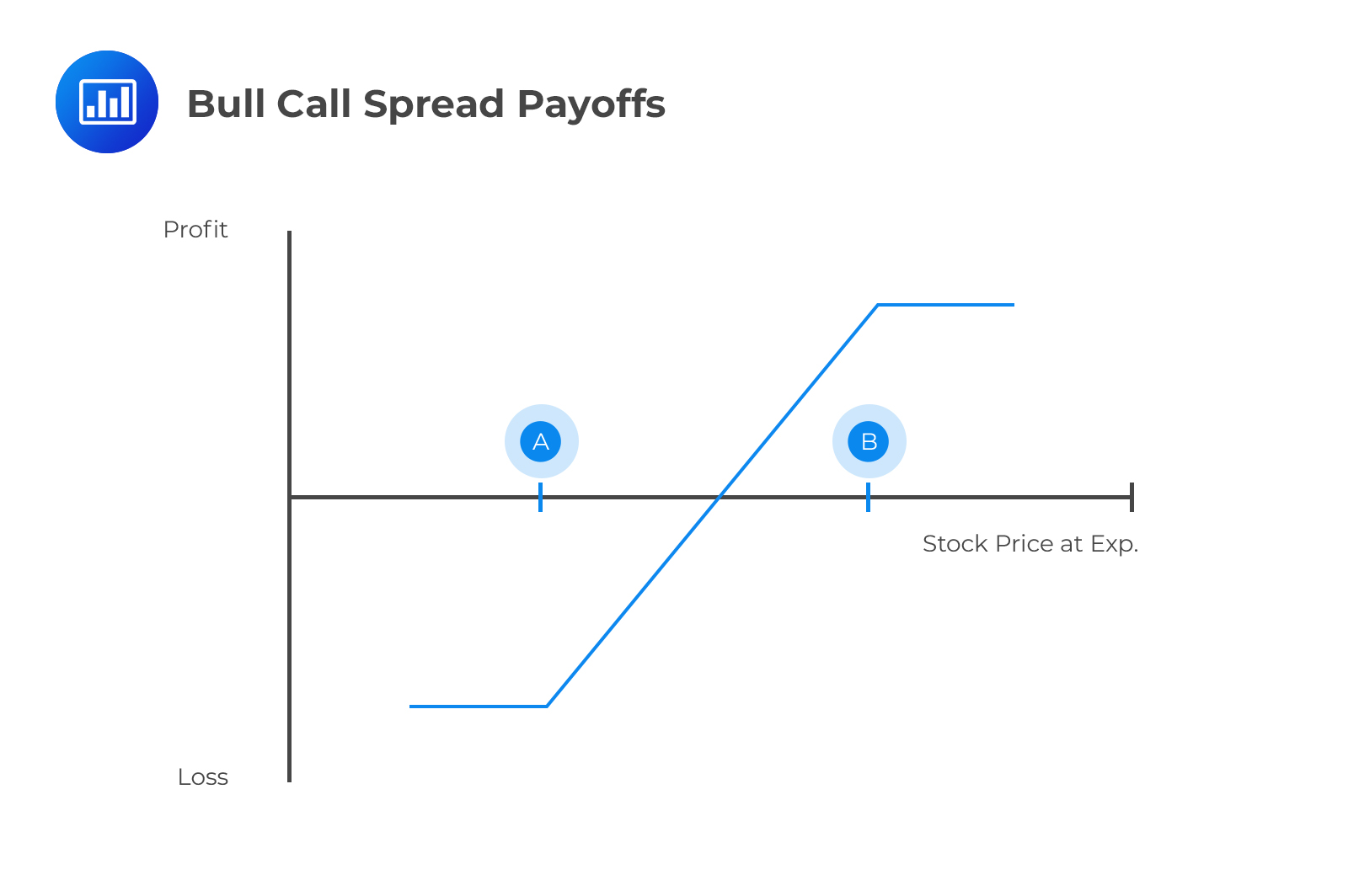
Being bullish, the buyer of a bull call spread expects the price of the underlying stock to rise but remain below the strike of the short call.

Example: Bull call spread

$$ \begin{array}{c|c} \text{Buy 1 ABC 100 call at} & \text{\$5.50} \\ \hline \text{Sell 1 ABC 105 call at} & \text{\$2.00} \\ \hline \text{Net cost} & \text{\$3.50} \\ \end{array} $$

The premium paid for the lower strike is higher than the premium received for the higher strike because the lower strike has higher chances of being attained in the near term.

In a bull put spread, the bullish trader buys a put with a lower strike and simultaneously sells a put with a higher strike. The premium received from the sale of the higher strike put is higher than the premium paid for the lower strike put. As such, the two positions generate a positive net income.

Example: Bull put spread

$$ \begin{array}{c|c} \text{Sell 1 ABC 100 put at} & \text{\$3.5} \\ \hline \text{Buy1 ABC 95 put at} & \text{\$1.8} \\ \hline \text{Net cost} & \text{\$1.70} \\ \end{array} $$

The cost of this spread is limited to the net premium received. The maximum loss, on the other hand, is capped by the long put.

Note: In both call and put spreads, the expiration date, as well as the underlying asset, must be the same for both positions.

A bull spread limits the investor’s upside as well as the downside risk. This can be explained as follows:

An investor has a call option with a strike price \(X_1\). He chooses to give some of higher potential by selling a call option with a strike price \(X_2 > X_1\). In return the investor earns a price of the option with a strike price \(X_2\).

Example: Bull spread payoff

Tony Adams has paid $2.50 to purchase a $50 strike call with an expiry of 6-months. To reduce his exposure to adverse price movements, he has entered into an alternative 6-month contract that obliges him to sell the underlying asset to the holder at a strike price of $54.

The holder of this second contract has paid Adams $1.40 to obtain the right to buy the underlying assets from Adams.

You are given that the continuously compounded risk-free rate of return applicable over the term of the contract is 5%, and the price of the underlying asset on maturity is $52.

Calculate Adams’s total payoff and profit.

Solution

Adams is long on the $50 strike call and will thus exercise his right on maturity because the underlying asset price is higher than the strike price. His payoff from this contract will be:

$$\text{Payoff}_{\$50\ strike\ call}=\max{\left(0,\$52-$50\right)}=\$\ 2$$

On the $54 strike call, Adams is in the short position. Because the underlying asset price on maturity is lower than the strike, the option expires out of the money, and Adams gets to keep the premium received at the onset.

The payoff would thus be:

$$\text{Payoff}_{\$54\ strike\ call}=-\max{\left(0,\$52-\$54\right)}=0$$

The total payoff will thus be:

$$\$\ 2+\$\ 0=\$\ 2$$

To compute the profit, we have to first compute the cost of setting up the two positions:

$$\text{Net cost}=-\$\ 2.5+\$\ 1.4=-\$\ 1.1$$

The accumulated cost on expiry

$$=-1.1e^{0.05\times0.5}=-\$\ 1.1278$$

The overall profit will thus equal to:

$$ 2- 1.1278=\$\ 0.872$$

Bear spread

A bear spread is a bearish options strategy designed to take advantage of a moderate decline in the price of the underlying in the near term. A bear call spread consists of one short call with a lower strike price and one long call with a higher strike price. On the other hand, a bear put spread consists of one long put with a higher strike price and one short put with a lower strike price.

Example: Bear Spread Strategy

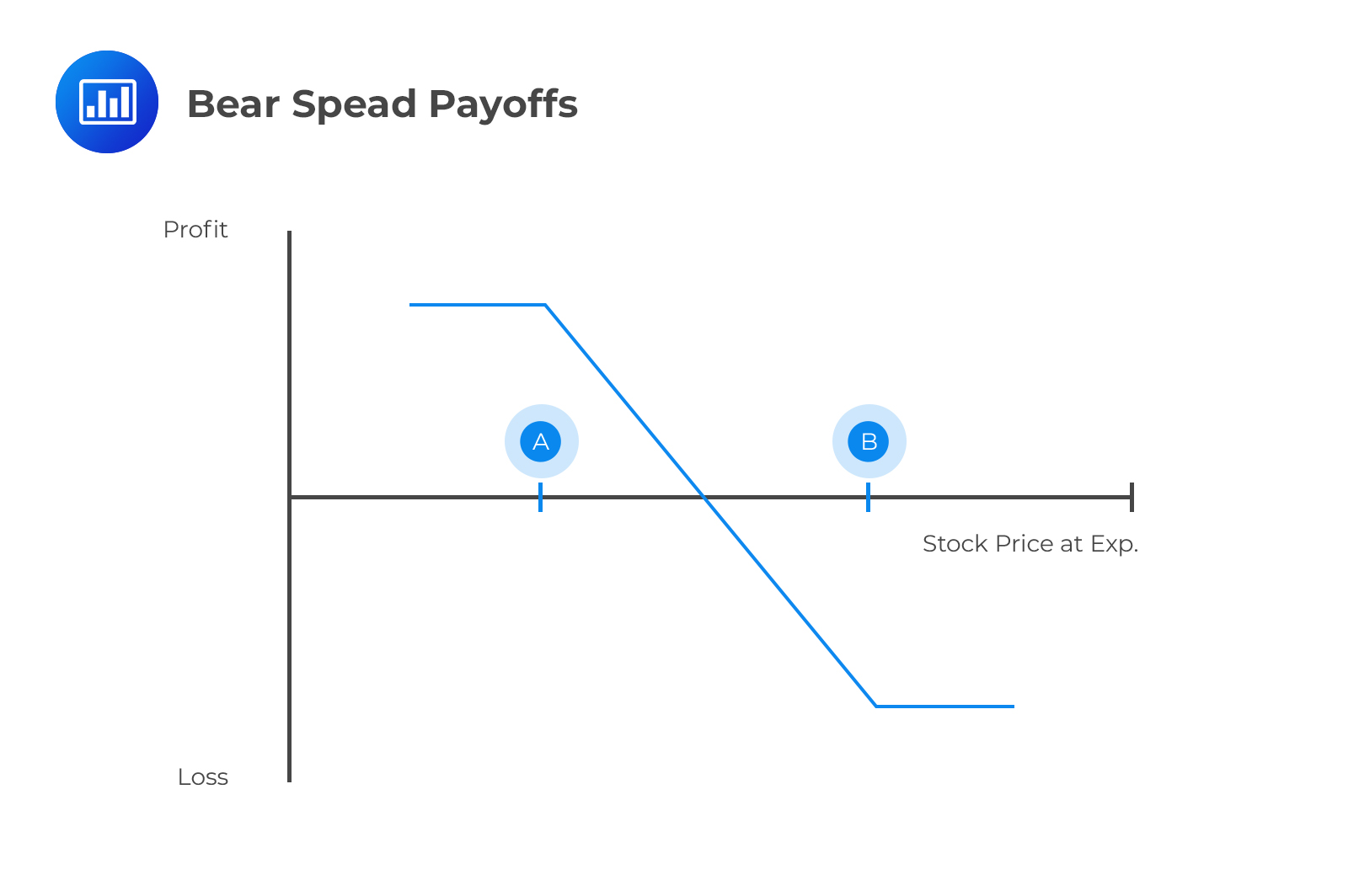
Tony Adams has paid $1.80 to purchase a $50 strike put with an expiry of 6-months. To reduce his exposure to adverse price movements, he has entered into an alternative 6-month contract that obliges him to buy the underlying asset from the holder at a strike price of $45.

The holder of this second contract has paid Adams $0.60 to obtain the right to sell the underlying assets to Adams.

You are given that the continuously compounded risk-free rate of return applicable over the term of the contract is 5%, and the price of the underlying asset on maturity is $46.

Calculate Adams’s total payoff and profit.

Solution

Adams is long on the $50 strike put and will exercise this option because the strike price is higher than the price of the underlying asset on maturity. His payoff from this contract will be:

$$\text{Payoff}_{\$50\ strike\ put}=\max{\left(0,\$50-\$46\right)}=\$4$$

On the $45 strike put, Adams is in the short position. Because the underlying asset price on maturity is higher than the strike, the option expires out of the money, and Adams keeps the premium received at the onset.

The payoff would thus be:

$$\text{Payoff}_{\$45\ strike\ call}=-\max{\left(0,\$52-\$54\right)}=0$$

The total payoff will thus be:

$$\$4+\$0=\$4$$

To compute the profit, we have to first compute the cost of setting up the two positions:

$$Net\ cost=-\$1.8+\$0.6=-\$1.2$$

The accumulated cost on expiry

$$=-1.2e^{0.05\times0.5}=-\$1.2304$$

The overall profit will thus equal to

$$\$4-\$1.2304=\$2.7696$$

Butterfly Spread

A butterfly spread is a neutral, limited risk strategy that involves a combination of various bull and bears spreads. The holder combines four options contracts having the same expiry date at three strike price points. Two option contracts are bought – one at a higher strike price and one at a lower strike price – and two option contracts are sold at a strike price in between. A butterfly trader has reason to believe the underlying asset will not move too far away from the current price.

Take for example an investor buying a call option at a lower strike price of \(X_1 (A)\), purchasing a call option at a relatively high strike price of \(X_3 (C)\), and selling two call options at a price of \(X_2 (B)\) in between \(X_1 (A)\) and \(X_3 (C)\).

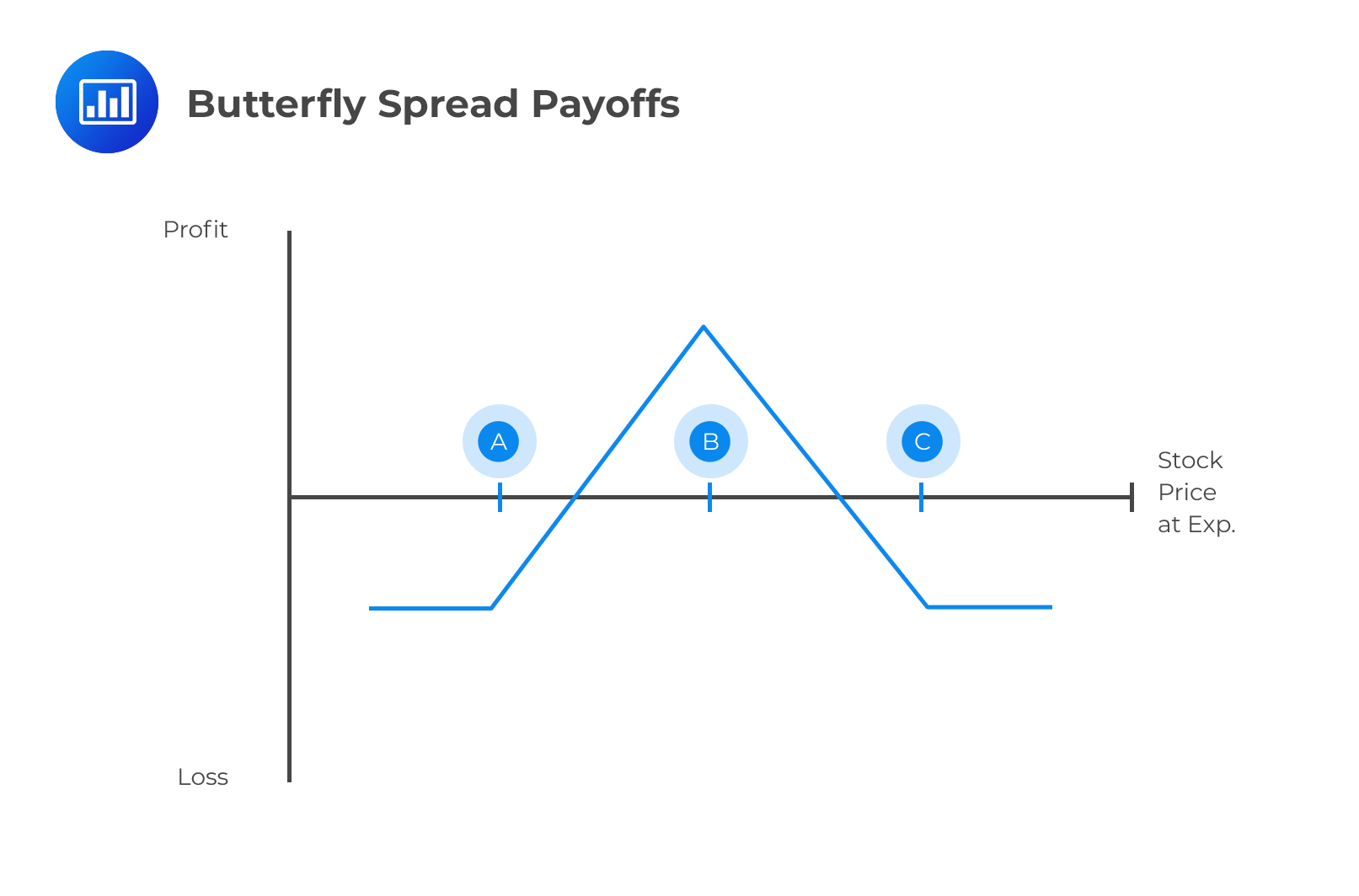Now the table below which shows the payoff from the butterfly spread.

$$ \begin{array}{c|c|c|c|c} \begin{array}{c} \text{Range of the} \\ \text{share price} \end{array} & \begin{array}{c} \text{The payoff from the} \\ \text{1st long call} \end{array} & \begin{array}{c} \text{The payoff from the} \\ \text{2nd long call} \end{array} & \begin{array}{c} \text{Payoff from the} \\ \text{(short call)} \end{array} & \begin{array}{c} \text{Total profit} \\ \text{(Payoff)} \end{array} \\ \hline {S_T \le X_1} & 0 & 0 & 0 & 0 \\ {X_1 < S_T < X_2} & {S_T-X_1} & 0 & 0 & {S_T-X_1} \\ {X_2 < S_T < X_3} & {S_T-X_1} & 0 & {-2(S_T-X_2)} & {X_3-S_T} \\ {S_T \ge X_3} & {S_T-X_1} & {S_T-X_3} & {-2(S_T-X_2)} & 0 \\ \end{array} $$

From the table above, it is easy to see that profits are realized if \(X_2\) stays close to the current share price. This strategy, therefore, is appropriate to an investor who feels that the share price movements are minimal or rather unlikely.

Example: Butterfly Spread

The following information is provided concerning certain options trading in the market

• The price of a $55 strike call is $12;
• The price of a $65 strike call is $6;
• The price of a $60 strike call is $8;
• All calls have a term of 6 months; and
• The continuously compounded risk-free rate of return applicable over the term of the contracts is 4% per annum.

Joseph Praise has created a strategy by selling two $60 strike calls and purchasing one of each of the $55 strike and $65 strike calls.

At maturity, the price of the underlying asset was $64.

Calculate Joseph’s overall payoff and profit from the strategy

Solution

Joseph is short on the $60 strike call. The holder will thus exercise and receive the following payoff:

$$\text{Payoff}_{\$60\ call}=2\times\left(\max{\left(0,64-60\right)}\right)=\$ 8$$

Joseph’s payoff will be:

$$2\times\left(-\max\left(0,64-60\right)\right)=-\$8$$

Joseph is long on the $55 strike call. His payoff will be:

$$\text{Payoff}_{\$55\ call}=\max{\left(0,64-55\right)}=\$9$$

Joseph is long also on the $65 call. Because the underlying security price is lower than the strike price, the option expires out of the money. Joseph’s payoff is thus:

$$\text{Payoff}_{\$65\ call}=\max{\left(0,64-65\right)}=\$0$$

The total payoff is thus:

$$\$9-\$8+\$0=\$1$$

To compute the profit, we determine the net cost of setting up the strategy:

$$cost=\left(2\times8\right)-12-6=-\$2$$

Joseph’s overall profit is thus:

$$\$1-\$2e^{-0.04\times0.5}=-\$0.6375$$

Ratio Spread

This is a strategy where options are traded in such a way that an investor buys a certain number of options (m) and sells (n) options of the same underlying asset and the exercise date at a different strike price. This strategy is taken when the investor has reason to believe that the stock price will be volatile in the near future.

Graphically, it can be represented in many different ways, but to calculate the payoff and profit, it is always the same process: Add up the payoffs or profits of the individual options bought or sold.

Example: Ratio Spread Payoff

An investor has constructed a put ratio spread by purchasing a $58 strike put for $1.50 and selling two $61 strike put options each at a price of $0.90. All the contracts have 6 months expiry term and are based on the shares of Footlink Limited.

On maturity, Footlink shares were trading at $59.50 per share, and the continuously compounded risk-free rate of return applicable over the contract term is 4%

Calculate the payoff and profit to the investor for holding this spread.

Solution

The investor is long on the $58 strike put and would not exercise the option as the strike price is lower than the price of the underlying on maturity. His payoff is thus:

$$\text{Payoff}_{\$58\ put}\max{\left(0,58-59.9\right)}=0$$

The investor is short on the $61 strike put and is thus obliged to sell the underlying assets to the holder.

His payoff will be:

$$\text{Payoff}_{\$61\ put}=\ -2[max(61-59.5,0)]=-\$3$$

The overall payoff from the two positions is thus -$3. The accumulated net cost of setting up the contracts is:

$$\left(1.8-1.5\right)e^{0.04\times0.5}=0.3061$$

The overall profit is, therefore:

$$0.3061-3=-\$2.6939$$

Payoff Functions of Combination Strategies

A combination is a type of option strategy that involves taking positions in both calls and puts on the same stock such as shares. We cover the different strategies below.

Straddle

A straddle involves two transactions on the same security, with positions that offset one another. A short straddle (left-side image) is created by selling a call and a put with the same strike price and expiration. A long straddle (right-side image) is created by purchasing a call and a put with the same strike price and expiration.

Example: Straddle

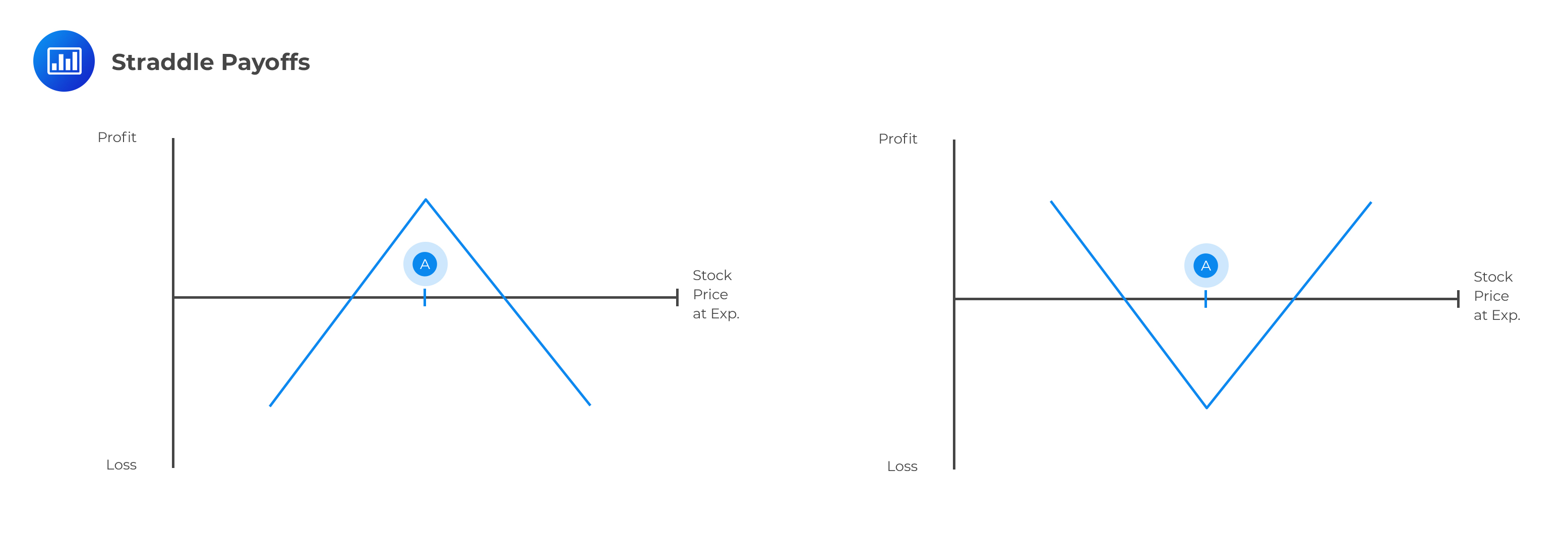
The strike price of a 3-month call and its identical put is $45. The prices of the call and the put are $1.80 and $1.20, respectively, and are based on the underlying ABC Limited shares. An investor has created a strategy by purchasing the 3-month call and the put.

On maturity, ABC shares were trading at the NYSE at a price of $43 per share, and you are given that the continuously compounded risk-free rate of return over the contract term was 5% per annum.

Calculate the investor’s payoff and profit.

Solution

The security price is lower than the strike price. The payoff to the call will be:

$$max\left(0,43-45\right)=\$0$$

The payoff to the put will be:

$$max\left(0,45-43\right)=\$2$$

The overall payoff will thus be \(2+0=\$2\).

The profit to the investor will be:

$$\left[\left(-1.80-1.20\right)^{0.05\times0.25}\right]+2=-\$1.00375$$

Strangle

Similar to the straddle, a long strangle consists of a long call and a long-put option on the same underlying asset and with the same expiration date. In a strangle, however, the two options have different exercise prices.

Example: Strangle

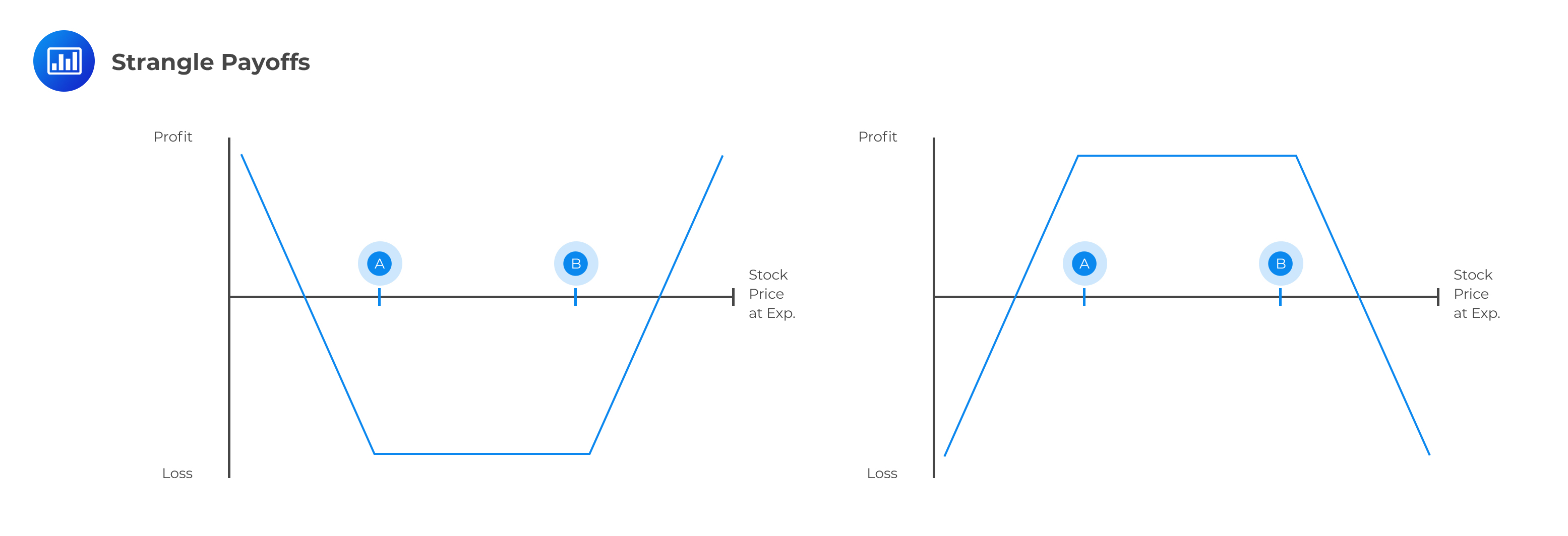
The price of a 3 month $50 strike call option is $2. The price of a 3 month $48 put is $4. An investor has set up a strategy by purchasing the two options.

At maturity, the price of the underlying asset was $53. The continuously compounded risk-free rate of return over the term is 4% per annum.

Calculate the payoff and profit to the investor.

Solution

The security price on maturity is higher than the strike price for the call. The option will therefore be exercised and would result in a payoff of:

$$\text{Payoff}_{\$50call}=max\left(0,53-50\right)=\$3$$

The put expires out of the money, and its payoff equals:

$$\text{Payoff}_{\$48\ put}=\text{max}\left(0,48-53\right)=0$$

The total payoff from the two positions is thus:

$$ \ $3+\$0=\$3$$

To compute the profit, we determine the cost of setting up the two positions:

$$\text{Cost of the strategy}=\left(2+3\right)e^{0.04\times0.25}=\$5.05$$

The overall profit from the strategy is thus:

$$ \begin{align}\text{Profit}&=\text{Payoff}-\text{Cost of Strategy}\\&=\$3-\$5.05=-\$2.05\end{align}$$

Collar

A collar is a strategy where an investor purchases a put and sells a call option with a higher strike on the same underlying assets. Both the call and the put have the same expiration date.

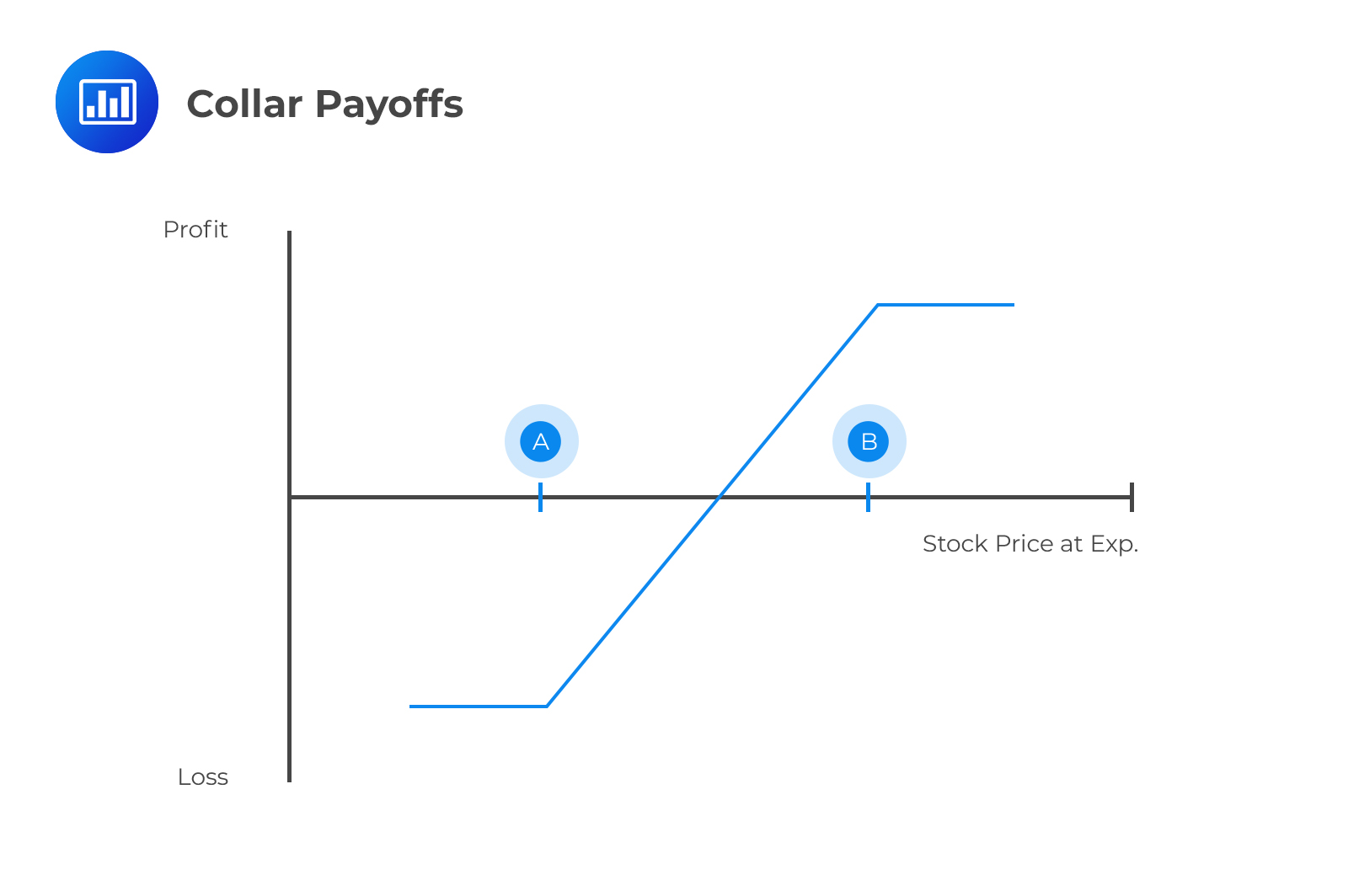
The difference between the put and call strikes is known as the collar width.

Example: Collar Strategy

Hannah Watkins currently holds 100 shares of ABC Limited. The shares are trading at the NYSE at $12 per share. ABC limited issued a profit warning and structural changes in management in their just-concluded half-year report and briefing. Hannah fears that this move may impact her holding and has thus paid $6.50 to enter into a contract that gives her the right but not obligation to sell all her shares in 6 months at a strike price of $11 per share.

However, to safeguard against her projections being wrong, she sells another contract that obliges her to sell to another investor the same shares at a price of $14 per share in 6 months. She has received $5 for the transaction.

The continuously compounded risk-free rate of return over the 6 months is 4% per annum, and we are given that ABC shares had a price of $10.5 per share on maturity.

Calculate Hannah’s payoff and profit.

Solution

The first contract is a put option; which is a contract that gives the holder the right but not obligation to sell a specified underlying asset at a given price on a given future date.

From the definition, we see that Hanna is in a long position on the put and will have the right to sell her shares at $11 on maturity. She pays a premium of $6.5 for this contract.

The second contract is a call option; which is a contract that gives the holder the right but not obligation to buy a specified underlying asset at a given price on a given future date.

Because Hannah has sold the contract, she is in a short position and will be obliged to sell her shares at a price of $14 per share. She receives a premium of $5 from this contract.

Call Option

Because the security price on maturity is lower than the strike price, the call expires out of the money. The resulting payoff is:

$$\text{Payoff}=100\times-(\max(\left(0,10.5-14\right))=0$$

Put Option

Hannah is long on the $11 strike put. Because the strike price is higher than the underlying asset price on maturity, she exercises her right to sell. Her payoff from the transaction is:

$$100\times\max{\left(0,11-10.5\right)}=$50$$

Her total payoff will thus be:

$$\$50+\$0=\$50$$

Note that payoff ignores the cost of setting up the strategy, that is, the option premium.

The accumulated net cost of setting up the collar strategy will be:

$$\left(-6.5+5\right)e^{0.04\times0.5}=-\$1.53$$

Her profit from the transaction is thus:

$$\begin{align} \text{Profit} &= \text{Payoff} – \text{Accumulated Net Cost of Strategy}\\ \$50-\$1.53 =\$48.47 \end{align}$$

If Hannah had instead held the shares without using a collar, her shares would be $150 less worthy. However, by using the collar, the potential loss is reduced by the ($48.47) profit from the two positions.

General Properties of Options that Affect Option Prices

Factors Affecting Option Prices

Let \(S_0\) denote the current stock price, \(K\) the strike price of the option,  \(r\) the short-term risk-free interest rate, \(D\) the present value of the dividends from the underlying stock, \(\alpha\) the expected volatility over  and \(T\) the time to expiration of the option.

Current Stock Price, \(S_0\)

The value of all call options increases (decreases) as \(S_0\) increases (decreases). For put options, the value of the put decreases (increases) as \(S_0\) increases (decreases).

The Strike Price of the Option, \(K\) or (\X\)

For call options, the value decreases (increases) as \(K\) increases (decreases). For put options, the value increases (decreases) as \(K\) increases (decreases).

Time Expiration

With American style options, as the time to expiration increases, the value of the option increases. With more time, there are higher chances of the option moving in-the-money.

However, the same does not apply to European-style options, precisely when the underlying has scheduled dividends. For example, assume we have a two-month call option, a four-month call with the same exercise price, and the same underlying stock. Assume further that a sizeable dividend is expected in three months. The ex-dividend stock price and call price will decrease. As such, the two-month call could be more valuable than the four-month call.

Risk-free Rate over the Lifespan of the Option, \(r\)

As the risk-free rate increases, the value of a call (put) increases (decreases).

Dividends, \(q\)

As the dividend increases, the value of a call (put) decreases (increases). The reason behind this is that immediately after payment of a dividend, the stock price falls. The call option holder has no access to the dividends because they do not own the underlying stock.

Expected Volatility of Stock Price Over Time, \(\sigma\)

Volatility is considered the most significant factor in the valuation of options. As volatility increases, the value of all options increase. In particular, the maximum loss on a call is limited to the premium paid. Thus, as volatility increases, there are higher chances of the option expiring in-the-money

Put-call Parity in European Options

Put-call parity states that the price of a call option implicitly informs a certain price for the corresponding put option with the same strike and expiration and vice versa.

Stocks with no Dividends

Consider the following portfolios:

• Portfolio A: One call option plus an amount of cash equivalent to \(Xe^{rT}\); and
• Portfolio B: One put option plus one share.

Let \(S_T\) be the security price at time \(T\), and \(X\) be the strike price of both the put and the call option.

The value of portfolio A at time \(T\) will be such that:

If \(S_T > X\) the value is given by:

$$S_T-X+X=S_T$$

If \(S_T < X\) the value of the portfolio is given by:

$$0+X=X$$

The value from portfolio A depending on whether the call has been exercised or not is:

$$\max(S_T,X)$$

The value of portfolio B at time \(T\) will be:

If \(S_T > X\);

$$0+S_T=S_T$$

If \(S_T < X\);

$$X+S_T-S_T=X$$

The value from portfolio B, depending on whether the put has been exercised or not, is:

$$\max(X,S_T)$$

Since the options are European, they cannot be exercised before maturity. Thus, put-call parity demands that the value of the two portfolios today is the same.

If we let \(c_t\) and \(p_t\) represent the price of the respective call and put options at time \(t\), we can express the relationship mathematically as,

$$ c_t+Xe^{-r(T-t)}=p_t+S_t $$

Example: Put-Call Parity – Stock with no dividends

A stock currently sells for $51. A 3-month call option on the stock, with a strike price of $50, has a price of $5. Assume a 10% continuously compounded risk-free rate.

Determine the price of the associated put option.

Solution

We know that:

$$ c_t+Xe^{-r(T-t)}=p_t+S_t $$ Making \(p_t\) the subject, $$ \begin{align*} p_t & =c_t+Xe^{-r(T-t)}-S_t \\ & =5+50e^{-0.1×0.25}-51 \\ & =2.77 \\ \end{align*} $$

If \(p_t\) is greater than or less than $2.77, there will be arbitrage opportunities.

For example, assume \(p_t=$3.50\). The following arbitrage opportunities would present themselves:

1. Buy call for $5;
2. Short a put to realize $3.50;
3. Short the stock to realize $51; and
4. Invest $49.5 (=51+3.5–5) for 3 months, making \($50.75(=49.5e^{0.1×0.25})\).

Let \(S_T\) be the price of the stock at expiry.

If \(S_T > 50\),

• Receive $50.75 from investment; annd
• Exercise call to buy stock for $50.
• Net profit = $0.75

If \(S_T < 50\),

• Receive $50.75 from investment;
• The put is exercised by the holder: buy the stock for $50.
• Net profit = $0.75

Put-call parity is only valid for European options. For American options with the possibility of early exercise, the relationship turns into an inequality:

$$ S_0-X \le C-P \le S_0-Xe^{-rT} $$

Example 2: Put-Call Parity – Stock with no dividends

A one-year European put option on a non-dividend-paying stock with the strike at USD50 currently trades at USD5.55. The current stock price is USD45. The stock exhibits an annual volatility of 30%. The annual risk-free interest rate is 5%, compounded continuously.

Determine the price of a European call option on the same stock with the same parameters as those of this put option.

Solution

According to put-call parity,

$$ c_t+Xe^{-r(T-t)}=p_t+S_t $$

Making \(c_t\) the subject,

$$ \begin{align*} c_t & =p_t+S_t-Xe^{-r(T-t)} \\ & =5.55+45-50e^{-0.05×1} \\ & =2.99 \\ \end{align*} $$

Stock with Discrete Dividends

In case the dividends are expected at discrete time intervals, the put-call parity formula changes to:

$$c_t+Xe^{-r(T-t)}=p_t+S_t-D$$

Where  represents the present value of the dividend payments

Stock with Continuous Dividends

For a stock with a continuous dividend yield \(q\) , the put-call parity formula changes to:

$$c_t+Xe^{-r(T-t)}=p_t+S_te^{-q(T-t)}$$

Example: Put Call Parity – Stock with continuous dividends

An investor purchases a 4-month European put option on a share currently trading at $109 for $0.50. The put’s strike price is $110, and the share pays dividends continuously at the rate of 12% per annum. The current risk-free force of interest is 9%.

Calculate the price of the corresponding European call option.

Solution

For a stock with continuously paid dividends, the put-call parity formula is given as:

$$c_t+Xe^{-r(T-t)}=p_t+S_te^{-q(T-t)}$$

Thus:

$$c_t+109e^{-0.09\times\frac{4}{12}}=0.5+110e^{-0.12\times\frac{4}{12}}$$

Solving for \(c_t\) we get:

$$c_t=0.4083$$

Options with Respect to Term to Maturity and Strike Price

Term to Maturity

The time to maturity of an option influences the value of an option. The longer the time, the higher the chance that the underlying asset’s prices will move to the buyer’s advantage.

This is because the buyer has unlimited upside potential. In the event of a price movement against the buyer, the buyer’s maximum loss is the option premium paid to the writer.

Thus, given two simple options with the same strike price, the value of the option with a longer-term will be higher than the value of the option with a shorter term, holding all other things constant.

Strike Price

The strike price of an option affects its intrinsic value. The intrinsic value of an option defines the profit that would be obtained if the option was to be exercised immediately.

For the call option, the higher the strike price, the lower the value of the option. On the other hand, for a put option, the higher the strike price, the higher the value of the option.

Factors Affecting the Early Exercise of American Options

Call option holders have the right but not the obligation to buy shares as per the terms of the contract, but they do not hold shares. As such, they cannot benefit from the rights of shareholders such as the right to receive dividends – as long as the call options have not been exercised.

When the underlying stock pays dividends, a call option holder will not receive it unless they exercise the contract before the dividend is paid. Whoever owns the stock as of the ex-dividend date receives the cash dividend, so an investor who owns in-the-money call options may exercise early to capture the dividend.

In summary, a call option should only be exercised early to take advantage of dividends if:

1. The option is in-the-money; and
2. The time value of the option needs to be less than the value of the dividend.

It wouldn’t make sense to exercise an out-of-the-money call option and pay an above-market price just to receive a dividend.

Suitable conditions for early exercise of a put option include:

1. The option must be deep in-the-money;
2. High interest rates are prevalent in the market; and
3. Sufficiently low volatility.

Provided these conditions have been met, the holder of an American put option can exercise early, but only after the dividend has been paid. Clearly, it would make a whole lot more sense to exercise the put option the day after the dividend is paid in order to collect the dividend, instead of exercising the day before and missing out.

The contrast between the American and European options is that, with American options, the holder can exercise the option before the expiry date not on the expiry date as in European options. This should imply that the values of European and American should be equal if the expiry date is equal, other factors kept constant.

From the valuation option intrinsic value, if we compare the call and put options in terms of the strike price, a higher strike price means that lower intrinsic value and premium for the call option and higher intrinsic value and premium for the put option.

For the case of the time to maturity, the longer the time to maturity means that there is a higher chance of the share price to move in favor of the option before the expiry, therefore, the value of a call option may increase. The reverse happens to put options, which is clearly intuitive.