Asset Pricing Models

After completing this chapter, the Candidate will be able to:

1. Explain the Capital Asset Pricing Model (CAPM).
   • Recognize the assumptions and properties of CAPM
   • Calculate the required return on a particular asset, a portfolio or a project using CAPM.
2. Explain factor models
   • Recognize the assumptions of a factor model for security returns.
   • Identify the expected return, factors, factor betas, and firm-specific components of a security from its factor equation.
   • Calculate the required return on a particular asset, a portfolio or a project using a single-factor and a multi-factor model.

Asset Pricing Models build on the ideas discussed in the Modern Portfolio Theory (MPT), single and Multifactor Models to characterize the entire investment markets assuming that investor behavior will be as predicted by these models.

Two such models, sometimes referred to as equilibrium models, which we will cover in this chapter are:

• The Capital Asset Pricing Model – which extends on the assumptions of the Modern Portfolio Theory (MPT)
• Factor models – which include single and multifactor models.

The Capital Asset Pricing Model (CAPM)

The Capital Asset Pricing Model (CAPM) was developed by Sharpe, Lintner, and Mossin. It builds on the assumptions of the MPT.

CAPM gives a linear expected return-beta relationship that determines the expected return given a beta of an asset. Thus CAPM provides a transition from the total risk (a used in CML) to systematic risk as to the primary determinant of expected return. CAPM is usually implemented through the security market line (discussed later).

The general expectation in a competitive market is that if securities/investments have the same level of risk, they should have the same level of expected return.

Assumptions of the Capital Asset Pricing Model

The extra assumptions introduced by CAPM include:

• A risk-free rate exists in the market, and investors can borrow and lend unlimited amounts at this rate.
• The markets for risky assets are perfect, meaning investors have access to all the information that can affect the price of a given security.
• Investors have the same estimates of the expected returns, standard deviations, and covariance over the one-period horizon.
• All investors have the same one-period horizon.
• All investors measure in the same “currency” for example dollars or in “real” or “money” terms.
• There are no transaction costs.
• There are no taxes.
• There is perfect divisibility of assets, i.e., assets can be bought and sold in very small quantities.
• All assets are marketable or liquid, i.e., investors can transact in large quantities with little or no impact on the price.
• Unlimited short-selling is permissible.
• Investors are price takers whose individual buy and sell decisions do not affect the price.
• Investors’ utility functions are based solely on the expected portfolio return and risk.

Properties of Capital Asset Pricing Model

Investors will, in general, hold investments in both the risk-free assets and risky assets based on their own levels of risk aversion.

Investors have the same expectations about the rate of return on risky assets, variances of those returns, and their covariances: If this holds, then all investors will end up selecting the same portfolios from the efficient frontier of risky assets resulting in the market portfolio.

The market portfolio will contain the portfolio of securities whose returns are sensitive to systematic risks.

Investors are subject to the same risk-free rate of return under CAPM: If this holds, then the tangent line to the efficient frontier of risky assets will intercept the y-axis at the risk-free rate of interest.

The Security Market Line

The security market line (SML) is a graphical representation of the capital asset pricing model where beta (reflecting the systematic risk) on the x-axis and the expected return on the y-axis. The SML is shown below:

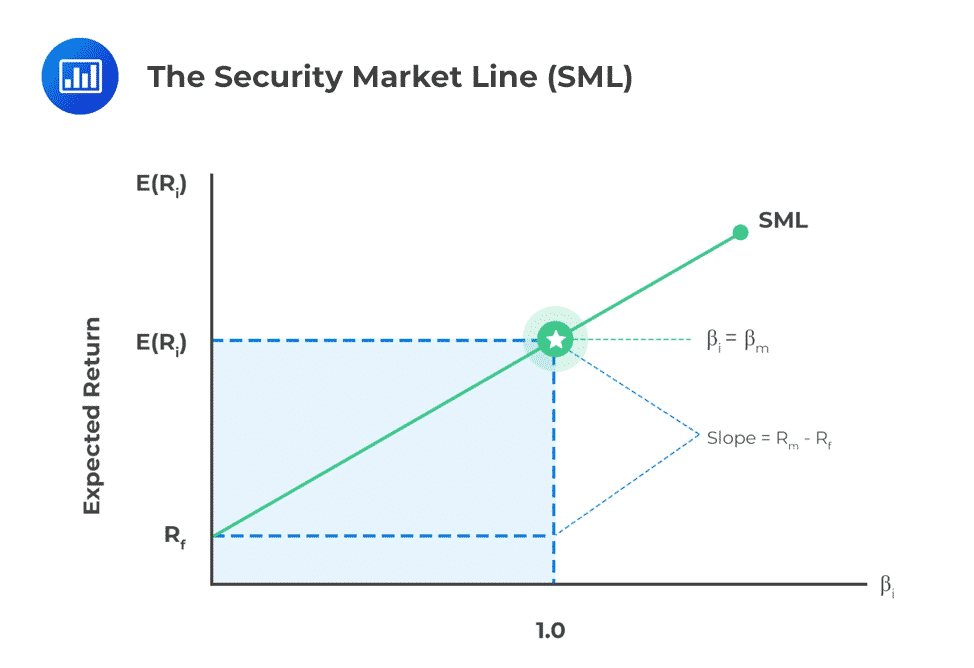
Note that the CML only considers efficient portfolios, whereas the security market line applies to both efficient and non-efficient portfolios.

The security market line equation is given by:

$$E_m=r+\beta_i(E_m-r)$$

This equation can be written as:

$$E_i=r+\beta_i(E_m-r)$$

Where:

\(E_i\)= the expected return on security \(i\)

\(r\)= the return on the risk-free asset

\(\beta_i\)= the beta factor of the security defined as \(\frac{Cov\left[R_i,R_m\right]}{Var(R_m)}\)

\(E_m\)= the expected return on the market portfolio

The Slope(\(E_m-r\)) of the security market is called the Equity Premium, as shown in the formula above.

The Beta of a Portfolio

Beta is a measure of systematic risk associated with a particular stock, asset, or portfolio. For a given asset, beta is given by:

$$B_i=\frac{Cov\left[R_i,R_m\right]}{Var(R_m)}$$

Where,

\(Cov(R_i, R_m)\) = covariance between the return of stock \(i\) and the return of the market

\(Var(R_m)\) = variance of the market portfolio.

Portfolio beta is then obtained as a weighted sum of the betas of the constituent securities making up the portfolio. That is:

$$\beta_p=\sum_{i=1}^{n}{w_i\beta_i}$$

Where

\(\beta_i\) = beta of asset \(i\) \(i=1,2,\ldots,n)\).

\(w_i\) = weight of asset \(i\)\ \((i=1,2,\ldots,n)\).

Note that:

$$\sum_{i=1}^{n}w_i=1$$

Therefore in the case of a two-asset portfolio (a risk-free asset and a risky asset), the portfolio beta is given by:

$$\beta_p=w_1\beta_1+w_2\beta_2$$

Therefore, the portfolio’s return as proposed by CAPM is given by:

$$E_p=r+\beta_p(E_m-r)$$

The equation above implies a linear relationship between the expected return of a portfolio and the systematic risk of the portfolio (\(\beta_p\)).

Example: Estimating the Beta of a Stock Using the CAPM

You are given the following information about a given market

• The risk-free rate is 4%;
• The expected return on the market portfolio is 10%;
• The standard deviation of the return of the market portfolio is 24%; and
• Stock A has a standard deviation of 30% and a correlation coefficient with the market of 0.45.

Calculate the Beta of Stock A.

Solution

Apply the formula we have defined above to estimate the Beta for Stock A.

$$\beta_A\ =\frac{Cov(R_A,R_M)}{Var(R_M)}$$

Where,

\(Cov(R_A, R_M)\) = The covariance between the return of stock A and the return of the market; and

\(Var(R_M)\) = The variance of the market portfolio.

Given the correlation coefficient between the return of stock and the market return, we can compute the covariance between stock A and the market return as:

$$COV\left(R_A,R_M\right)=\frac{\sigma_A\rho_{AB}}{\sigma_M}$$

Since

$$\text{Since Var} \left(R_M\right)=\sigma_M^2$$

Substituting the beta formula for values we get:

$$\beta_A\ =\frac{0.30\times0.45}{0.24}=0.5625$$

Interpreting this Result

The Beta for stock A is 0.5625. This means that for every 1% move of the market portfolio, stock A will move by 0.5625% in the same direction.

In general:

• A beta above 1 indicates a stock/asset/portfolio that has, historically, amplified the whole market (positive or negative). For example, a beta of 2 would mean that for every 1% move in the return of the market portfolio, the stock/asset will move twice as much.
• A beta of zero indicates the stock/asset or portfolio is insensitive to systematic risk. In this case, the return of this stock will equal the risk-free rate of return.
• A negative beta indicates that the stock return will move in the opposite direction with shocks in the market return arising from systematic risk.

Example: Calculating the Expected Return of a Portfolio using CAPM

Security A has a beta of 0.7, and Security B has a beta of 1.8. A risk-averse investor has invested 60% of his funds on Security A and 40% on security B. You are given that the risk-free rate of return is 5% and the expected return on the market portfolio is 12%.

Calculate the expected return on the portfolio made up of these two securities.

Solution

We are given the Beta of stocks A and B as 0.7 and 1.8, respectively.

$$\beta_p=\sum_{i} w_i\beta_i=0.7\times0.6+1.8\times0.4=1.14$$

$$E_p=r+\beta_p(E_m-r)$$

Using the formulas:

Where:

\(r\) = The risk-free rate of interest;

\(E_m\) = The expected return on the market portfolio.

Substituting the formula for values gives:

$$E_p=0.05+1.14\left(0.12-0.05\right)=12.98\%$$

Limitations of the Capital Asset Pricing Model

Some of the limitations of CAPM are outlined below:

• The assumption of a risk-free lending and borrowing rate may not hold in practice. Generally, investors in the real world will be subjected to different rates of lending and borrowing.
• CAPM assumes no taxes. In practice, investors will be subject to charges, such as the capital gains tax. If this is taken into account, then the expected return computed using CAPM may be underestimated.
• CAPM assumes that investors will select their portfolios from the market portfolio. In practice, investors will be open to a universe of opportunities to choose from and thus would not always select the said market portfolio.
• The expected returns of securities are based on historical performance, which may not reflect the future outcome.
• Assumptions of investor behavior like risk aversion may not hold in practice as normal markets will comprise investors with different risk appetites.

Factor Models

Factor models are financial models that incorporate different risk elements in the market to determine the expected return on an asset or security.

These models incorporate macroeconomic, fundamental, and statistical factors to characterize the market and help calculate the required return on an asset or security.

Below we describe macroeconomic, statistical, and fundamental factor models:

Macroeconomic factor models – These use observable historical time series factors such as interest rates, inflation, and economic growth in a bid to estimate the influence these factors may have on future returns of a portfolio or security.

Fundamental factor models – These use company-specific variables to compare the sensitivity of a portfolio to one of the factors within the factors of a benchmark portfolio. Some of these fundamental factors would include the price-earnings ratio, the industry the company is operating in, etc.

Statistical factor models – These make use of principal component analysis to determine as much as possible the set of factors or indices that explain as much as possible the relationship between the risk and return of a given portfolio.

Expected Return, Factors, Factor Betas, and Firm-Specific Components of a Security from its Factor Equation

A factor can be defined as a variable that explains the expected return of an asset.

A factor-beta measures the sensitivity of the return on a given asset to a specific factor. The bigger the factor, the more sensitive the asset return is to that factor.

Let  denote a component-specific factor affecting the return of an asset

Using a factor model, the required return of a stock return can be given as:

$$R_i=a_1+\beta_iF\cdots+e_{i\ }$$

Where,

\(R_i\)= rate of return on stock i

\(a\) = The constant factor with relation to security i

\(\beta_i\)= sensitivity of the stock’s return to a one-unit change in factor F

\(e_i\)= portion of the stock’s return unexplained by macro factors or, more generally, the error term. It usually has a mean of zero.

The part \(\beta_i+F+e_i\) of the formula above is called the systematic return of security \(i\). In contrast, the remaining factor is called the specific return, which is unique and independent of systematic return factors.

The expected return on the stock can then be expressed as:

$${E(R}_i)=E(a)+\beta_iE(F)+{E(e}_{i\ })=a+\beta_iF$$

The expected return from a factor model can thus be seen as a linear function of the security’s constant independent return and the sensitivity of the security returns to a specific factor.

Single-Factor and Multi-Factor Models

Suppose a factor model only incorporates one factor representing a single element of the systematic risk affecting the return on a security. In that case, the model will be said to be a single-factor model.

Using the single-factor model, the required return on an asset is given as:

$$R_i=a+\beta_iF+e_{i\ }$$

The expected return on an asset using a single factor model can be expressed as:

$${E(R}_i)=a+\beta_iF$$

The variable \(a\) here represents the constant independent return, \(\beta_i\) the sensitivity of the returns in response to a change in the factor, and \(F\) the market premium in response to the factor.

In this case, the systematic risk of the factor will equal the total risk of the asset.

An example of a single index model is the CAPM, which limits the risk to one source, that is, the covariance with the market portfolio.

If we combine more than one factor to construct our efficient portfolio, each factor will capture different elements of the systematic risk of the resulting asset return. Such a model is known as a multi-factor model.

Thus, a multi-factor model is a financial model that employs multiple factors in its calculations to explain asset prices. Such models introduce uncertainty stemming from multiple sources.

Using the multi-factor model, the required return on an asset is given as:

$${E(R}_i)=a+\beta_iF_1+\beta_2F_2+\ldots+\beta_nF_n+e$$

The expected return on an asset using a multi-factor model can be expressed as:

$${E(R}_i)=a+\beta_iF_1+\beta_2F_2+\ldots+\beta_nF_n$$

Where \(\beta_i\) represent the sensitivity of the asset returns to factor \(F\) and \(F_i(i=1,2\ldots n)\) the market premium with respect to the factor \(F\).

An example of a multi-factor model is the Arbitrage Pricing Theory

Example: Calculating the required Return of an Asset using the Single-factor Model

Assume the common stock of Blue Ray Limited (BRL) is examined with a single-factor model, using unexpected percent changes in GDP as the single factor. Assume the following data is provided:

• Risk-Free Rate = 10%
• GDP factor-beta = 1.50
• Expected GDP growth = 4%

Compute the required rate of return on BRL stock, assuming there’s no new information regarding firm-specific events.

Solution

$$R_i=a_1+\beta_iF+e_i$$

$$=10\%+1.5\times4\%$$
$$=16\%$$

Example: The Expected Return of an Asset Using the Multi-factor Model

Assume the common stock of BRL is examined using a multifactor model based on two factors: unexpected percent change in GDP and unexpected percent change in interest rates. Assume the following data is provided:

• Constant Mean specific return = 10%
• GDP factor-beta = 1.50
• Interest rate factor-beta = 2.0
• Expected growth in GDP = 2%
• Expected growth in interest rates = 1%

Compute the required rate of return on BRL stock, assuming there’s no new information regarding firm-specific events.

Solution

We know that our formula for a multifactor model is given as:

$$R_i=R_f+\beta_{i1}F_1+\beta_{i2}F_2$$

Substituting the formula for values we get:

$$R_i=10\%+1.5\times2\%+2.0\times1\% =15\%$$

The Arbitrage Pricing Theory

This model was developed by Stephen Ross in 1976. It assumes a market in equilibrium but does not rely on strong assumptions of CAPM. Its basis is built from multifactor models and assumes that the investment environment is arbitrage-free.

The APT theory describes expected returns as a linear function of exposures to common macroeconomic risk factors.

$$E(R_i)=R_F+\beta_{i1}RP_1+\beta i2RP_2+\beta_{i3}RP_3+\cdots+\beta_{iK}RP_K$$

Where,

\(RP_j\) = The excess return over the risk-free rate attached to a risk factor; and

\(\beta_{i1}\) = The sensitivity of the stock return to one unit change in factor \(j\).

Expanding the above formula, we get the APT equation as follows:

$$E\left(R_i\right)=R_F+\beta_{i1}\left[E\left(R_1\right)-R_F\right]+\beta_{i2}\left[E\left(R_2\right)-R_F\right]+\beta_{i3}\left[E\left(R_3\right)-R_F\right]+\cdots\ \ \ \ \ $$$$+\beta_{iK}[E(R_K)-R_F]$$

Assumptions of the APT Model

• Well-diversified portfolios can be formed.
• No arbitrage opportunities exist.
• Returns follow a -factor process.

The main strength of the APT approach is that it is based on the no-arbitrage investment world. However, it does not explain the best multifactor model and the size of the constants.

Example: Calculating the Expected Return using The Arbitrage Pricing Theory

The following data exists for asset A:

• Risk-free rate = 3%,
• GDP factor beta = 0.40,
• Consumer sentiment factor beta = 0.20,
• GDP risk premium = 2%,
• Consumer sentiment risk premium = 1%

Calculate the expected return for Asset using a 2-factor APT model.

$$E(R_A)=0.03+0.4(0.02)+0.2(0.01)=0.04=4\%$$

Note: Both CAPM and APT describe equilibrium expected returns for assets. CAPM can be considered a special case of the APT in which there is only one risk factor – the market factor.