Determinants of Interest Rates
After completing this chapter, the candidate will be able to: Define and... Read More
AnalystPrep’s Actuarial Exams Preparation Materials
For our question bank, study notes, quizzes, and all our video lessons: https://analystprep.com/shop/learn-practice-package-for-soa-exam-fm/
After completing this chapter, the candidate will be able to:
A bond is a financial instrument that promises to pay interest payments at the stated future time over a period of time (term of the bond) and pay lump sum value, also called redemption value, at the end of the term (maturity date).
The interest payments made at a regular interval of time is called coupon payments. These payments can be fixed, and hence the bond will be called fixed-rate bonds. However, some bonds do not have coupon payments and are called zero-coupon bonds or accumulation bonds. There are also those bonds that possess a characteristic where the interest rates fluctuate over its term, and those are called floating-rate bonds.
Bonds are usually issued by the government or companies to raise capital to maintain projects, pay an outstanding loan, or any other issue that requires finances. Think of a bond as a loan. The issuer (borrower) issues a bond with detailed information on the term of the bond, the interest payments (coupon payments), and the time at which the loan principle will make (maturity time). As you will realize, bond calculations are quite analogous to that of loans.
Determining the price of a bond involves three approaches:
This is a commonly used formula. Denote:
\(P\) – The price of the bond
\(i\) – The yield rate (as a periodic effective interest rate)
\(R\) – The redemption value
\(F\) – The face value of the bond (often called par value)
\(r\) – The coupon rate (as a periodic effective interest rate)
\(C\) – The coupon payment (C=F\( \cdot \) r)
The timeline of a bond is given below:
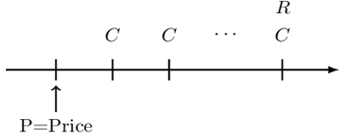
Then by basic formula, the price of a bond is given by:
$$ \text{P}=\text{Fr}.\text{a}_\overline { \text{n}| }+\text{R}\text{v}^{\text{n}} $$
Where
\( \text{v}^\text{n}=\left({1}+\text{i}\right)^{-\text{n}}\)
Note that \(Fr\) represents the annual coupon payments \((C)\). From this formula, it is clear to see that the price of the bond is equal to the present value of its future cash inflows. When the redemption value is equal to the face value, the bond is described as a par-value bond or redeemable at par. An important point here is to note that if no redemption is specified, either directly or indirectly, then you should assume a bond is a par-value bond.
An investor buys $10,000 nominal of a 5-year fixed-interest bond redeemable at par. The bond pays an 8% coupon semiannually in arrears.
What price should the investor pay to obtain a yield rate of 10%?
Consider the following timeline:
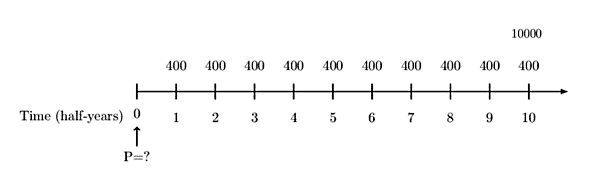 Using the basic formula, the price of a bond is given by:
Using the basic formula, the price of a bond is given by:
$$ \begin{align*} \text{P}&=\text{Fr}\text{a}_\overline { \text{n}| } +\text{R}\text{v}^\text{n} \\ \Rightarrow \text{P}&=10,000\times0.04.\text{a}_{\overline{10|}}@5\%+10,000\text{v}^{10}@5\%\\ & 9,227.83 \end{align*} $$
Alternatively, you could use your TVM buttons on your calculator, with the parameters N=10, I/Y=5, PMT=400, and FV=10,000, then CPT PV. However, your calculator should be in end mode with P/Y=C/Y=1.
The discount derived from the basic formula. We know that:
$$ \text{P}=\text{Fr}\text{a}_\overline { \text{n}| }+\text{R}\text{v}^\text{n} $$
But,
$$ \text{a}_\overline { \text{n}| }=\cfrac{1-\text{v}^{\text{n}}}{\text i}\Rightarrow \text{v}^\text{n}=1-\text{i}.\text{a}_\overline { \text{n}| } $$
Therefore the basic formula can be written as:
$$ \begin{align*} \text{P} & =\text{Fr}\text{a}_\overline { \text{n}| }+\text{R}\left(1- \text i\text{a}_\overline { \text{n}| }\right)\\ & =\text{R}+(\text{Fr}-\text{Ri})\text{a}_\overline { \text{n}| } \\ \therefore \text{P}-\text{R} & =(\text{Fr}-\text{Ri})\text{a}_\overline { \text{n}| } \end{align*} $$
The variables in this formula are defined as before. \( \text{Fr}-\text{R}.\text{i} \) represents the better “version” of Fr relative to expected interest rate payments \( \ \text{R}.\text{i}\).
If \( \text{Fr}-\text{R}.\text{i}> {0}\) then the bond will pay higher interest, and hence the buyer is willing to pay extra \( \text{P}-\text{R} \) that will be redeemed at maturity. This extra amount is called the premium, and thus, the bond is said to be bought at a premium. In other words, a bond sells at a premium if \(r>i \) and thus:
$$ \text{Premium}=\text{P}-\text{R}=(\text{Fr}-\text{Ri})\text{a}_\overline { \text{n}| } $$
On the other hand, if \( \text{Fr}-\text{R}.\text{i}<\text{0}\) ,then the buyer will not buy the bond unless it is offered at a discount, that is, when the price of the bond \((P\)) is less than redemption value \((R\)). In this case, we say that the bond bought at a discount. Conversely, a bond sells at a discount if \(r<i\) and thus:
$$ \text{Discount}=\left|\text{P}-\text{R}\right|=\text{R}-\text{P}=(\text{Fr}-\text{Ri})\text{a}_\overline{\text{n}| } $$
An investor buys $10,000 nominal of a 5-year fixed-interest bond redeemable at par. The bond pays an 8% coupon semiannually in arrears.
Calculate the premium of the bond at a yield rate of 5%.
$$ \begin{align*} \text{P}-\text{C} & =(\text{Fr}-\text{C} \text{i})\text{a}_\overline { \text{n}| }\\ & =\left(10000\times\frac{0.08}{2}-10000\times\frac{0.05}{2}\right)0.05\text{a}_{\overline{10|}}@\text{i}=\frac{5}{2}\%\\ & =\left(400-250\right)\text{a}_{\overline{10|}}@\text{i}=2.5\%=$1,312.81 \end{align*} $$
An 8-year 8% bond with a face value of $1,000 has a semiannual coupon. The price of the bond is such that the bond yields an 10% compounded semiannually.
Given that the discount on the bond is $250, calculate the price of the bond.
The discount of a bond is given by:
$$ \begin{align*} \text{R}-\text{P} & =(\text{Fr}-\text{Ri})\text{a}_\overline { \text{n}| } \\ \Rightarrow \text{R}-\text{P}& = 250\therefore \text{P}=\text{R}-250 \end{align*} $$
What remains is to calculate the amount of the redemption value, \(R\). By the basic formula, the price of a bond is given by:
$$ \text{P}=\text{Fr}.\text{a}_\overline { \text{n}| }+\text{R}\text{v}^\text{n} $$
In this case,
$$ \begin{align*} \text{P}&=1000\times\frac{0.08}{2}.\text{a}_{\overline {16|}@5\%}+\text{R}(1.05)^{-16}\\ \Rightarrow \text{R}-250&=1000\times\frac{0.08}{2}. \text{a}_\overline {16|}+\text{R}(1.05)^{-16} \\ &=40.\text{a}_{\overline {16|}@5\%}+\text{R}(1.05)^{-16}\\ \Rightarrow \text{R}&=\cfrac{250+40.\text{a}_\overline {16|}}{1-(1.05)^{-16}}=1,261.35 \end{align*} $$
Therefore the price of the bond is given by:
$$\text{P}=1,261.35-250=1,011.35$$
Using the same basic formula, we can derive the base formula. Let \(B\) be the base amount. The base amount is the amount such that when multiplied with the yield rate, it is equal to coupon payments of the bond. That is,
$$ \text{Bi}=\text{Fr} \\ \Rightarrow \text{B}=\frac{\text{Fr}}{\text{i}} $$
We know that,
$$ \begin{align*} \text{P} & =\text{Fr}\text{a}_\overline { \text{n}| }+\text{R}\text{v}^\text{n} \\ & =\left(\text{Bi}\right)\text{a}_\overline { \text{n}| }+\text{R}(1-\text{i}.\text{a}_\overline { \text{n}| })\\ & =\text{B}\left(1-\text{v}^\text{n}\right)+\text{R}\text{v}^\text{n}\\ \therefore \text{P} & =\text{B}+\left(\text{R}-\text{B}\right)\text{v}^\text{n} \\ \text{Where } \text{v}^\text{n} & =\left(1+\text{i}\right)^{-\text{n}} \end{align*} $$
From the formulation, if we let \(B\) be the amount of a loan, the excess amount that the bondholder will receive at maturity will be just a bonus. This makes the bond more valuable, and the buyer will be willing to pay the price greater than \(B\) otherwise, the bond buyer will not buy unless the price is less than the loan amount.
Intuitively, the redemption value \(R\) of the bond is equivalent to a loan for a certain period of time. The coupon payments \(Fr\) can be taken to be the interest payments that the borrower pays to prevent the loan from growing, and price \(P\) is the principal value of the loan.
The value \(P-R\) represents the extra value \(P-R>0\) (bond priced at a premium) or a shortfall \(P-R\).
A ten-year bond has annual coupons of $60 each and a redemption value of $2,400. The bond yields 10% per annum.
Calculate the price of the bond.
Using the base amount formula, we know that:
\( \therefore \text{P}=\text{B}+\left(\text{R}-\text{B}\right)\text{v}^\text{n} \)
Where:
$$ \Rightarrow \text{B}=\frac{\text{Fr}}{\text{i}}=\frac{60}{0.10}=600 $$
Thus,
$$ \text{P}=600+\left(2400-600\right)\text{v}^{10}=$\ 1,293.98 $$
The book value of a bond is the price of the bond at any time between the purchase and maturity date. Define:
\(\text{B}_\text{k}\) = The book value (amortized value) of bond immediately after the kth coupon.
Similar to loans, book value can be derived using prospective or retrospective methods.
Retrospectively, the book value of a bond is given by:
$$ \begin{align*} \text{B}_\text{k}&=\text{AV}\left(\text{P}\right)-\text{AV}\left(\text{Past Payments}\right)\\ &=\text{P}{(1+\text{i})}^\text{k}-\text{C}\cdot \text{s}_{\overline{\text{k}}|} \\ \therefore \text{B}_\text{k} & =\text{P}{(1+\text{i})}^\text{k}-\text{C}\cdot \text{s}_{\overline{\text{k}}|} \end{align*} $$
Prospectively, the book value of a bond is given by:
$$ \begin{align*} \text{B}_\text{k}&=\text{PV}(\text{Remaining Payments})\\ &=\text{C}\cdot \text{a}_{\overline{\text{n}-\text{k}|}}\ \ +\text{R}\cdot \text{v}^{\text{n}-\text{k}}\\ \therefore \text{B}_\text{k} & =\text{C}\cdot \text{a}_{\overline{\text{n}-\text{k}}|}+\text{R}\cdot \text{v}^{\text{n}-\text{k}} \end{align*} $$
Further, define the following:
\(\text{P}_\text{k}\) = The Amount of Principal Adjustment with the kth Coupon
Premium amortization in the case of bonds is equivalent to coupon payments minus the interest payments, which is basically \(\text{P}_\text{k}\). That is,
$$ \text{P}_\text{k}=\text{C}-\text{I}_\text{k} $$
The premium amortization can also be represented as (as shown above):
\( \text{P}_{ \text{k} }=\text{B}_{\text{k}-1}-\text{B}_\text{k}\)
Using the premium-discount formula, we can show that:
$$ \begin{align*} \text{P}_{ \textbf{k} }&=\text{B}_{\text{k}-1}-\text{B}_\text{k}\\ &=\left[\text{R}+(\text{Fr}-\text{Ri})\text{a}_\overline{\text n-\text k+1|}+\text{R}\right]-\left[\text{R}+(\text{Fr}-\text{Ri})\text{a}_\overline{\text{n}-\text{k}|}+\text{R}\right]\\ &=\left(\text{Fr}-\text{Ri}\right)\left[\text{a}_\overline{\text{n}-\text{k}+1|}-\text{a}_\overline{\text{n}-\text{k}|}\right]\\ &=\left(\text{Fr}-\text{Ri}\right)\text{v}^{\text{n}-\text{k}+1} \end{align*} $$
More interestingly, the amortization of premium over the kth period is presented by \( \text{P}_\text{k} \) and the accumulation of the discount is given by \( |\text{P}_\text{k} |\).
Recall that we denoted \( \text{P}_\text{k} \) as the amount of principal adjustment with the kth payment. What if now we need the amount of principal adjustment from time k to time m? We calculate this as the difference between the book values at times k and m. That is:
$$ \sum_{\text{j}=\text{k}+\text{1}}^{\text{m}}\text{P}_\text{j}=\text{B}_\text{k}-\text{B}_\text{m} $$
Recall that for loans, we defined \( \text{P}_\text{k} \) as the principal with kth payment so that:
$$ \sum_{\text{j}=1}^{\text{n}}\text{P}_\text{j}=\text{B}_0-\text{B}_\text{n}=\text{L}-0=\text{L} $$
Where \( \text{B}_0 \) is the loan balance at time 0 (which is basically the loan amount) and \( \text{B}_\text{n} \) is the loan balance after the nth payment and is equal to 0.
However, for the bonds, \( \text{B}_\text{n}=\text{R} \) so that
$$ \sum_{\text{j}=1}^{\text{n}}\text{P}_\text{j}=\text{B}_0-\text{B}_\text{n}=\text{P}-\text{R} $$
Where \( \text{B}_0 \) is the book value of a bond at time 0 (which is basically the price of a bond) and \( \text{B}_\text{n} \) is the book value at time n and is equal to R, the redemption value.
Additionally, the amount of interest earned from the time k to time m for a bond is equivalent to the sum of the payments after time k up to and including time m less the amount of principal adjustment from time k to time m. That is:
$$ \sum_{\text{j}=\text{k}+1}^{\text{m}}\text{I}_\text{j}= \sum_{\text{j}=\text{k}+1}^{\text{m}}\text{C}-\sum_{\text{j}=\text{k}+1}^{\text{m}}\text{P}_\text{j}\\ =\left(\text{m}-\text{k}\right)\cdot \text{C}-(\text{B}_\text{k}-\text{B}_\text{m}) $$
Similar to loans, we relate the “neighboring” book values. Consider the following timeline:
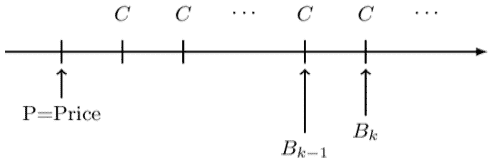
Where:
\( \text{B}_\text{k} \) = The book value just after the \(\text k^{\text{th}}\) coupon.
\( \text{B}_{\text{k}-1} \) = The book value just after \( \left(\text{k}-1\right)^{\text{th}} \) coupon.
Denote the book value of the bond before the kth coupon by \( \text{B}_\text{k}^{\text{bef}} \). Then,
$$ \text{B}_\text{k}^{\text{bef}}-\text{C}=\text{B}_\text{k}\Rightarrow \text{B}_\text{k}^{\text{bef}}=\text{B}_\text{k}+\text{C} $$
Similarly,
$$ \text{B}_\text{k}^{\text{bef}}=\text{B}_{\text{k}-1}\cdot\left(1+\text{i}\right) $$
Also, it is easy to see that,
$$ \text{B}_\text{k}=\text{B}_{\text{k}-1}\cdot\left(1+\text{i}\right)-\text{C} $$
Or
$$ \text{B}_\text{k}=\text{B}_{\text{k}-1}-\text{P}_\text{k} $$
Recall that we denoted coupon payment as \( \text{C}=\text{F}\cdot \text{r} \). Analogous to loans, the total payment, which in this case is the coupon payment, is given by:
$$ \begin{align*} \text{C}&=\text{I}_\text{k}+\text{P}_\text{k}\\ \Rightarrow \text{P}_\text{k} & =\text{C}-\text{I}_\text{k} \end{align*} $$
Note that \( \text{I}_\text{k} \) , the amount of interest earned during the kth period is defined as:
$$ \text{I}_\text{k}=\text{i}\cdot \text{B}_{\text{k}-1} $$
A bond amortization table for a bond is similar to that of a loan with a slight difference. We will consider a bond sold at a discount, premium, and at par.
You buy a 4-year 1,000 face value bond, redeemable at par, with 6% annual coupons.
Determine the price of the bond to yield a 3% annual effective.
The timeline for the bond is given below:
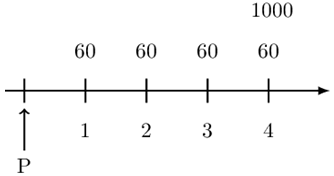
Using the basic formula, the price of a bond is given by:
$$ \begin{align*} \text{P} & =\text{Fr}.\text{a}_\overline{ \text{n}| }+\text{R}\text{v}^\text{n}\\ \Rightarrow \text{P} & =60\text{a}_{\overline{4}|0.03}+1000\text{v}_{0.03}^4=1,111.51] \end{align*} $$
Notice that \(P>R\) and thus the bond is said to be “bought at a premium” and the amount of the premium is:
$$ \text{P}-\text{R}=1,111.54-1,000=111.54 $$
Therefore, we say that a bond is sold at a premium of $111.54. The amortization table for the bond bought at a premium is given below:
$$ \begin{array}{c|c|c|c|l} {\textbf{Time} \\ \textbf{k} } & {\textbf{Payment} \\ \textbf{C} } & {\textbf{Interest } \\ \textbf{Earned} \\ \textbf{I}_\textbf{k} } & {\textbf{Principal} \\ \textbf{Adjustment} \\ \textbf{P}_\textbf{k} } & {\textbf{Book Value} \\ \textbf{B}_\textbf{k} } \\ \hline {0} & {} & {} & {} & {\text{B}_0=\text{P}=1111.51}\\ \hline {1} & {60} & {33.35} & {26.65} & {\text{B}_1=1084.86} \\ \hline {2} & {60} & {32.55} & {27.45} & {\text{B}_2=1057.41} \\ \hline {3} & {60} & {31.72} & {28.28} & {\text{B}_3=1029.13} \\ \hline {4} & {60} & {30.87} & {29.13} & {\text{B}_4=\text{R}=1000} \end{array} $$
We know that:
$$ \text{P}=\text{B}_0=1,111.51 $$
Assume that we lend a company $ 1,111.51 to earn 3% annually. We know that,
$$ \text{I}_\text{k}=\text{i}.\text{B}_{\text{k}-1} $$
And so,
$$ \text{I}_1=0.03\cdot1111.51=33.35 $$
However, at time 1, the company pays a coupon of $60. Therefore the company overpays the interest payments. And thus, the principal adjustment is given by:
$$ \begin{align*} \text{P}_\text{k} & =\text{C}-\text{I}_\text{k}\\ \text{P}_1& =60-33.35=26.65 \end{align*} $$
The principal adjustment is used to reduce the principal amount (the price of a bond). Thus,
$$ \text{B}_1=1111.51-26.65=1084.86 $$
Alternatively, we could calculate the book value of a bond retrospectively or prospectively. Retrospectively, the book value of a bond is given by:
$$ \begin{align*} \text{B}_\text{k} & =\text{P}\left(1+\text{i}\right)^\text{k}-\text{C}\cdot \text{s}_{\overline{\text{k}}|}\\ \Rightarrow \text{B}_1 & =1111.51(1.03)-60\text{s}_{\overline{1}|}=1084.86 \end{align*} $$
Prospectively,
$$ \begin{align*} \text{B}_\text{k} & =\text{C}\cdot \text{a}_{\overline{\text{n}-\text{k}}|}+\text{R}\cdot \text{v}^{\text{n}-\text{k}}\\ \Rightarrow \text{B}_1 & =60\text{a}_{\overline{3}|0.03}+1000\text{v}_{0.03}^3=1084.86 \end{align*} $$
A similar process is repeated until in time 4, where:
$$ \begin{align*} \text{P}_4 & =1029.13\\ \Rightarrow \text{I}_4 & =0.03\cdot1029.14=30.87 \end{align*} $$
And
$$ \text{B}_4=1029.14-29.12=1000 $$
Since for a bond \( \text{B}_\text{n}=\text{R} \), the bond above is completely repaid at time 4. Also, note that:
$$ \sum_{\forall \text{k}} \text{P}_\text{k}=\text{B}_0-\text{B}_\text{n}=\text{Premium} $$
For the case above, notice that:
$$ \sum \text{P}_\text{k}=111.51 $$
Moreover, \( \text{P}_\text{k} \) is a geometric sequence with the common ratio \(1+i\). In the case above, \( \text{P}_\text{k} \) is a geometric sequence with a common ratio
$$ \frac{27.45}{26.65}=\frac{28.28}{27.45}=\frac{29.13}{28.28}=1.03=1+\text{i} $$
When a bond is bought at a premium, we say it is written down since the book values are systematically decreasing from \( \text{B}_{0}=\text{P} \) to \( \text{B}_\text{n}=\text{R} \). The \( \text{P}_\text{k} \) values are positive and called the amortization of premium or amount of write down for a period (installment).
You buy a 4-year 1000 face value bond, redeemable at par, with 3% annual coupons.
Determine the price of the bond to yield 6% annual effective.
The timeline of the described bond is given below:
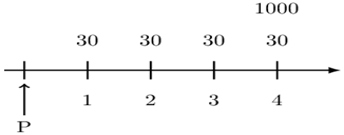
Using the basic formula, the price of the bond is:
$$ \text{P}=30\text{a}_{\overline{4}|0.06}+1000\text{v}_{0.06}^4=896.05 $$
Notice that \(P<R\) and thus the bond is said to “bought at a discount” and the amount of discount equals \(|P-R|\). Thus for the bond described above, the bond is bought at a discount of:
$$ \left|896.05-1000\right|=103.95 $$
$$ \begin{array}{c|c|c|c|l} {\textbf{Time} \\ \textbf{k} } & {\textbf{Payment} \\ \textbf{C} } & {\textbf{Interest } \\ \textbf{Earned} \\ \textbf{I}_\textbf{k} } & {\textbf{Principal} \\ \textbf{Adjustment} \\ \textbf{P}_\textbf{k} } & {\textbf{Book Value} \\ \textbf{B}_\textbf{k} } \\ \hline {0} & {} & {} & {} & {\text{B}_0=\text{P} =896.05}\\ \hline {1} & {30} & {53.76} & {-23.76} & {\text{B}_1 =919.81} \\ \hline {2} & {30} & {55.19} & {-25.19} & {\text{B}_2 =945.00} \\ \hline {3} & {30} & {56.70} & {-26.70} & {\text{B}_3 =971.70} \\ \hline {4} & {30} & {58.30} & {-28.30} & {\text{B}_4=\text{R} {=1000} } \end{array} $$
The same process to that of a bond bought at a premium is applied here. We know that:
$$ \text{I}_\text{k}={\text{i}.\text{B}}_{\text{k}-1} $$
So that:
$$ \text{I}_1=0.06\cdot896.05=53.76 $$
and
$$ \begin{align*} \text{P}_\text{k} & =\text{C}-\text{I}_\text{k}\\ \Rightarrow \text{P}_1 & =30-53.76=-23.76 \end{align*} $$
The idea here is that the borrower underpaid the lender by 23.76 at time 1. Thus, the book value at time 1 is:
$$ \text{B}_1=896.05-(-23.76)=919.81 $$
Note that you can calculate the book value of the bond using the prospective and retrospective methods.
We repeat the same process for times 2 and 3 so that at time 2:
$$ \begin{align*} \text{I}_2&=0.06\cdot919.81=55.19 \\ \Rightarrow \text{P}_2&=30-55.19=-25.19 \\ \therefore \text{B}_2&=919.81-(-25.19)=945.00 \end{align*} $$
For time 3,
$$ \begin{align*} \text{I}_3&=0.06\cdot945.00=56.70 \\ \Rightarrow \text{P}_3&=30-56.70=-26.70 \\ \therefore \text{B}_3&=945.00-(-26.70)=971.70 \end{align*} $$
At time 4, we expect the bond price to be completely paid. As such,
$$ \begin{align*} \text{I}_4&=0.06\cdot971.70=58.30 \\ \Rightarrow \text{P}_4&=30-58.30=-28.30 \\ \therefore \text{B}_4&=971.70-(-28.30)=1000 \end{align*} $$
Also, note that for a bond bought at a discount:
$$ \left|\sum_{\forall \text{k}} \text{P}_\text{k}\right|=\left|\text{B}_0-\text{B}_\text{n}\right|=\text{Discount} $$
For the case above, notice that:
$$ \left|\sum \text{P}_\text{k}\right|=-103.95 $$
Moreover, \( \text{P}_\text{k} \) is a geometric sequence with the common ratio \(1+i\).
When a bond is bought at a discount, we say it is written up since the book values are systematically increasing from \( \text{B}_0=\text{P} \) and \( \text{B}_\text{n}=\text{R} \). The \( \text{P}_\text{k} \) values are negative and |\( \text{P}_\text{k} \)| is called the accumulation of discount or amount of write up for period (installment) k.
You buy a 4-year 1000 face value bond, redeemable at 1,200, with 3% annual coupons.
Determine the price of the bond to yield 2.5% annual effective.
The timeline for the bond is:
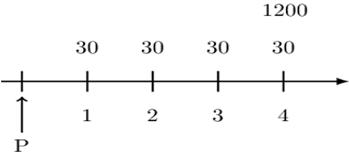
$$ \text{P}=30\text{a}_{\overline{4}|0.025}+1200\text{v}_{0.025}^4=1,200 $$
Since \(P=R\), we say that the bond is said to be “bought at par.” Note the difference with “redeemable at par.” Redeemable at par implies \(F=R\).
Following the same processes, the amortization table for a bond bought at par is given below:
$$ \begin{array}{c|c|c|c|l} {\textbf{Time} \\ \textbf{k} } & {\textbf{Payment} \\ \textbf{C} } & {\textbf{Interest } \\ \textbf{Earned} \\ \textbf{I}_\textbf{k} } & {\textbf{Principal} \\ \textbf{Adjustment} \\ \textbf{P}_\textbf{k} } & {\textbf{Book Value} \\ \textbf{B}_\textbf{k} } \\ \hline {0} & {} & {} & {} & {\text{B}_0=\text{P} =1200}\\ \hline {1} & {30} & {30} & {0} & {\text{B}_1 =1200} \\ \hline {2} & {30} & {30} & {0} & {\text{B}_2 =1200} \\ \hline {3} & {30} & {30} & {0} & {\text{B}_3 =1200} \\ \hline {4} & {30} & {30} & {0} & {\text{B}_4=\text{R} =1200} \end{array} $$
Notice that the coupon payments are exactly equal to the interest rate payments. Also, the following properties hold:
Generally, we know that a bond is bought at par if the coupon payments are equal to interest payments in each period so that:
$$ \text{F}\cdot \text{r}=\text{i}\cdot \text{B}_\text{k} $$
However, for a bond bought at par:
$$ \text{B}_0=\text{B}_1=\ldots \text{B}_\text{k}=\ldots\ =\text{B}_\text{n}=\text{R} $$
Therefore, a bond is bought at par if and only if
$$ \text{F}\cdot \text{r}=\text{R}\cdot \text{i} $$
A 20-year 1000 face value bond, redeemable at par, with 6% semiannual coupons, is bought to yield 4% compounded semiannually for the first ten years and 8% compounded semiannually after that. Determine the amount of the principal adjustment from the end of year 7 through the end of year 12.
Consider the following timeline:
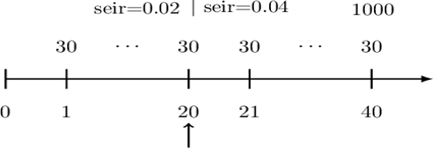
We need
$$ \text{P}_{14,24}=\text{B}_{14}-\text{B}_{24} $$
Now, using the prospective method:
$$ \text{B}_{24}=30\text{a}_{\overline{16}|0.04}+1000\text{v}_{0.04}^{16}=883.48 $$
To find \( \text{B}_{14} \) we need to find \( \text{B}_{20} \) which can be done in two ways. Consider the timeline below:
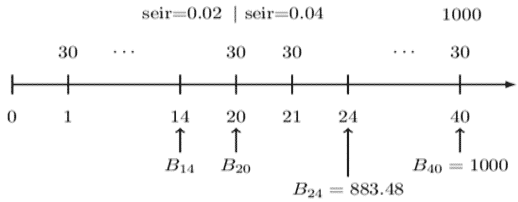
Prospectively,
$$ B_{20}=30a_{\overline{20}|0.04}+1000v_{0.04}^{20}=864.10 $$
Or
$$ \begin{align*} \text{B}_{20} & =30\text{a}_{\overline{4}|0.04}+883.48\text{v}_{0.04}^4=864.10 \\ \Rightarrow \text{B}_{14} & =30a_{\overline{6}|0.02}+\text{B}_{20}\cdot \text{v}_{0.02}^6=935.34 \end{align*} $$
Thus,
$$ \begin{align*} \text{P}_{14,24} & =\text{B}_{14}-\text{B}_{24}\\ & =935.34-883.48=51.86 \end{align*} $$
A callable bond is a bond in which the issuer reserves the right to redeem the bond at different discrete times (referred to as calling the bond), possibly for different redemption values.
When a callable bond is bought, no one knows when the bond will be called (redeemed); however, it can only be called at one of the times agreed upon at issue. Callable bond problems will be obvious by the wording of the problem. Unless told that the bond is callable within the wording of the problem, assume all bonds are held to maturity and redeemed for the stated or implied redemption value.
$$ \begin{array}{c|c} {\textbf{Time at which bond is called} \\ \textbf{n} } & {\textbf{Price in order to receive the desired yield rate} \\ {\textbf{P}(\textbf{i})} } \\ \hline {} & {} \\ \hline {} & {} \\ \hline {} & {} \\ \hline {} & {} \end{array} $$
$$ \begin{array}{c|c} {\textbf{Time at which bond is called} \\ \textbf{n} } & {\textbf{Yield rate that produces the given price } \\ {\textbf{i}}}\\ \hline {} & {} \\ \hline {} & {} \\ \hline {} & {} \\ \hline {} & {} \end{array} $$
A 1000 face value 20-year callable bond with 3% annual coupons can be redeemed according to the following schedule:
Determine the maximum price a buyer should pay in order to earn an annual yield of at least 5%.
We need to populate the following table and choose the lowest price at 5% yield rate:
$$ \begin{array}{c|c} {\textbf{Time at which bond is called} \\ \textbf{n} } & {\textbf{Price in order to receive the desired yield rate} \\ {\textbf{P}(\textbf{i})=\textbf{P}(\textbf{0}.\textbf{05})}} \\ \hline {10} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{10}}|}+\textbf{1000}\textbf{v}^{\textbf{10}}=\textbf{845}.\textbf{57}} \\ \hline {14} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{14}}|}+\textbf{1000}\textbf{v}^{\textbf{14}}=\textbf{802}.\textbf{03}} \\ \hline {15} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{15}}|}+\textbf{1075}\textbf{v}^{\textbf{15}}=\textbf{828}.\textbf{48}} \\ \hline {17} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{17}}|}+\textbf{1075}\textbf{v}^{\textbf{17}}=\textbf{807}.\textbf{24}} \\ \hline {18} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{18}}|}+\textbf{1125}\textbf{v}^{\textbf{18}}=\textbf{818}.\textbf{15}} \\ \hline {20} & {\textbf{P}=\textbf{30}\textbf{a}_{\overline{\textbf{20}}|}+\textbf{1125}\textbf{v}^{\textbf{20}}=\textbf{797}.\textbf{87}} \end{array} $$
Therefore, the maximum price is:
$$ \text{P}=797.87 $$
A 1000 face value 20-year callable bond with 3% annual coupons can be redeemed according to the following schedule:
You buy the bond for 797.87. Determine the effective annual yield if the bond is redeemed at the end of year 16.
According to the schedule given, the equation of value is given by:
$$ 797.87=30\text{a}_{\overline{16}|\text{i}}+1075\text{v}^{16}\\ \Rightarrow \text{i}=5.204\% $$
A 1000 face value 10-year callable bond with 8% semiannual coupons is bought for 1050. The bond can be redeemed at the end of any year, starting with year 7.
Determine the minimum annual effective yield for this bond.
Note that there is no redemption value stated or implied. For all bond problems, when this is the case, assume the bond is redeemable at par. Consider the following table:
$$ \begin{array}{c|c} {\textbf{Time at which bond is called} \\ \textbf{n} } & {\textbf{Yield rate to produce the given price} \\ {\textbf{i}:\ \textbf{P}(\textbf{i})=\textbf{1050}}} \\ \hline {14} & {1050=40\text{a}_{\overline{14}|}+1000\text{v}^{14}\ \ \ \ \Rightarrow\ \ \ \ \text{i}=3.54\%} \\ \hline {16} & {1050=40\text{a}_{\overline{16}|}+1000\text{v}^{16}\ \ \ \ \Rightarrow\ \ \ \ \text{i}=3.58\%} \\ \hline {18} & {} \\ \hline {20} & {} \end{array} $$
The interest rates will systematically increase or decrease (increase in this problem) when the redemption value remains the same. Therefore, we only need to check endpoints (the first column, i.e., n=14) for the same redemption values.
From the table, we choose the lowest yield rate:
$$ \Rightarrow \text{i}=3.54\% $$
However, notice that the above interest rate is a semiannual effective interest rate, but we need an annual effective interest rate.
$$ \Rightarrow \text{aeir}={1.0354}^2-1=7.21\% $$