Annuities/cash flows with non-contingent payments

AnalystPrep’s Actuarial Exams Preparation Materials

For our question bank, study notes, quizzes, and all our video lessons: https://analystprep.com/shop/learn-practice-package-for-soa-exam-fm/

After completing this chapter, the candidate will be able to:

1. Define and recognize the definitions of the following terms:annuity-immediate, annuity due, perpetuity, payable m-thly or payable continuously, level payment annuity, arithmetic increasing/decreasing annuity, geometric increasing/decreasing annuity, term of annuity.
2. For each of the following types of annuity/cash flows, given sufficient information of immediate or due, present value, future value, current value, interest rate, payment amount, and term of annuity, calculate any remaining item.
   • Level annuity, finite term.
   • Level Perpetuity.
   • Non-level annuities/cash flows.
     • Arithmetic progression, finite term and perpetuity.
     • Geometric progression, finite term and perpetuity.
     • Other non-level annuities/cash flows.

 

Definition and Terminology

An annuity is a series of regular payments. It is described as certain if it is payable for a known period of time (term of an annuity which can be an integer or not), and it is non-contingent, i.e., it does not depend on some factor such as death.

If the regular payments are equal amounts, then it is described as a level annuity. Otherwise, the annuities may vary, that is, it may be simply decreasing or increasing. For example, a payment of 50 dollars in five years, 100 in ten years, … , 400 dollars in forty years.

The annuity start date is at the beginning of the first period, and the annuity end date is at the end of the last period.

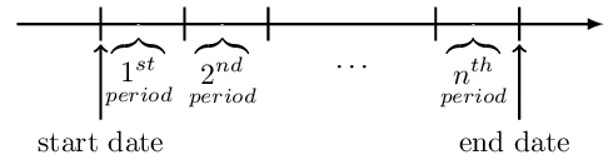
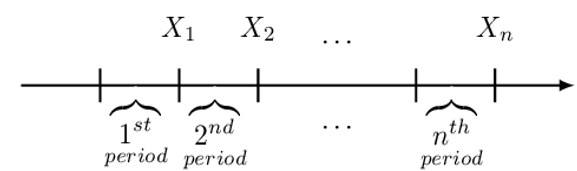
If the payments are paid at the end of each period, it described as paid in arrear, and it is called an annuity-immediate (or an ordinary annuity) as illustrated in the diagram below:

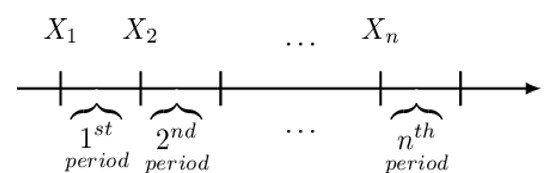
If the payments are made at the beginning of each period, they are paid in advance, and it is known as an annuity-due, as shown in the diagram below.

All financial calculations have a valuation date. The value of an annuity at the valuation date is the single sum value at the valuation date in which one is indifferent to receiving instead of receiving the periodic payments that form the annuity.

In this chapter, we will concentrate on the basic level annuity. A basic level annuity is a sequence of periodic payments, all of which are equal to 1.

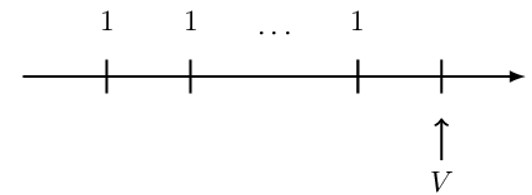
Where

\(V\) = The value at the valuation date of a basic level annuity.

A perpetuity is an annuity in which the payments continue forever. A perpetuity has no end date. Perpetuity is illustrated in the figure below:

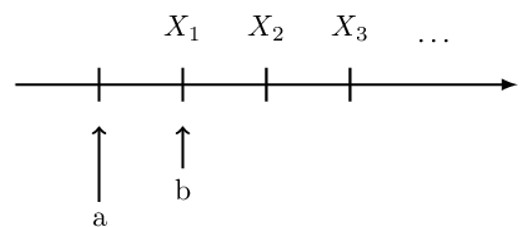
Where a is the start date for a perpetuity immediate

And b is the start date for perpetuity due.

Level Annuities

Basic Annuity-immediate

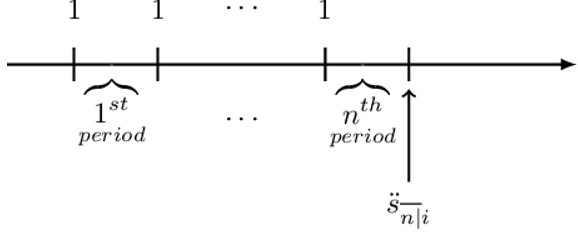
Consider n payments made at the end of each period. This means that the first payment is made at time 1, and the last payment is made at time n. The present value of these payments is denoted as. \( \text{a}_{\overline{\text{n}}|\text{i}} \) read as “a angle n at rate i”. .\( \ \text{a}_{\overline{\text{n}}|\text{i}} \) is defined as the value of a basic annuity immediate at the annuity start date (or equivalently the value of a basic level annuity, one (payment) period before the first payment).

It is illustrated by a timeline below:

Note that i is the periodic effective interest rate. If i=0, then clearly \(\textbf{a}_{\overline{\textbf{n}}|}={\textbf{0}}\). Otherwise, n payments of 1 unit made at the end of each of the next n time periods is given by (we shall drop the subscript i by assuming that there is no ambiguity in a given problem):

$$ \text{a}_{\overline{\text{n}}|}=\text{v}^1+\text{v}^2+\ldots+\text{v}^\text{n} $$

Note the above is a finite geometric expression given by:

$$ \text{S}_\text{n}=\frac{\text{a}_1(1-\text{r})}{1-\text{r}} $$

Where \(\text{a}_1\) is the first term, and r is the common ratio. Applying this formula in the annuity immediate expression, we have

$$ \begin{align*} &=\frac{\text{v}(1-\text{v}^\text{n})}{1-\text{v}} \\ &=\frac{\text{v}(1-\text{v}^\text{n})}{\text{v}{(\text{v}}^{-1}-1)} \text{ where } \text{v}=\frac{1}{1+\text{i}} \\ &=\frac{1-\text{v}^\text{n}}{1+\text{i}-1}=\frac{1-\text{v}^\text{n}}{\text{i}} \end{align*} $$

So the closed rule formula for the annuity immediate is:

$$ \text{a}_{\overline{\text{n}}|}=\frac{1-\text{v}^\text{n}}{\text{i}} $$

Example: Annuity Immediate

Calculate the present value of a series of payments of 1000 dollars payable at the end of each year from 2005 to 2010, assuming 10% effective rate of interest.

Solution

$$ \begin{align*} \text{a}_{\overline{\text{n}}|}&=\frac{1-\text{v}^\text{n}}{\text{i}}=1000a_{\overline{5}|}@10\% \\ &=1000\times\frac{1-{1.1}^{-5}}{0.1} \\ &=1000\times3.7908=3790.80 \text{ dollars} \end{align*} $$

Annuity-Immediate Payable m-thly

Now consider annuity payments of 1 made m times per year. The formulae changes by adding the superscript (m) at the right corner of the symbol. However, note that the annuity is still payable annual amount of 1 consisting of nm payments, with the amount of \( \frac{1}{\text{m}} \) each. Therefore,

$$ \text{a}_{\overline{\text{n}}|}^{(\text{m})}=\frac{1-\text{v}^\text{n}}{\text{i}^{(\text{m})}} $$

This can be proved from the first principles using the finite geometric formula.

$$ \begin{align*} \text{a}_{\overline{\text{n}}|}^{\left(\text{m}\right)}&=\sum_{\text{t}=1}^{\text{mn}}{\frac{1}{\text{m}}\text{v}^\frac{\text{t}}{\text{m}}} \\ &=\frac{1}{\text{m}}\left[\sum_{\text{t}=1}^{\text{mn}}\text{v}^\frac{\text{t}}{\text{m}}\right] \\ &=\frac{1}{\text{m}}\frac{\text{v}^\frac{1}{\text{m}}\left(1-\text{v}^\text{n}\right)}{1-\text{v}^\frac{1}{\text{m}}}=\frac{1}{\text{m}}\frac{\text{v}^\frac{1}{\text{m}})\left(1-\text{v}^\text{n}\right)}{\text{v}^\frac{1}{\text{m}}\left[\frac{1}{\text{v}^\frac{1}{\text{m}}}-1\right]} \\ &=\frac{1-\text{v}^\text{n}}{\text{m}\left[\left(1+\text{i}\right)^\frac{1}{\text{m}}-1\right]}=\frac{1-\text{v}^\text{n}}{\text{i}^{\left(\text{m}\right)}} \end{align*} $$

Notice that we used the relationship:

$$ \begin{align*} 1+\text{i}&=\left(1+\frac{\text{i}^{(\text{m})}}{\text{m}}\right)^\text{m} \\ \Rightarrow\text{i}^{\left(\text{m}\right)}&=\text{m}\left[\left(1+\text{i}\right)^\frac{1}{\text{m}}-1\right] \end{align*} $$

The main point here is to recall the relationship between effective and nominal interest rates.

Example: Basic Annuity Immediate Payable m-thly (Upper m)

Consider a 3-year annuity immediate paying 1 per year. The payments are made quarterly, the first payment made at the end of the first quarter. We need to find a closed rule expression for this annuity.

Solution

Consider the following timeline. Note that the arrow points the valuation date.

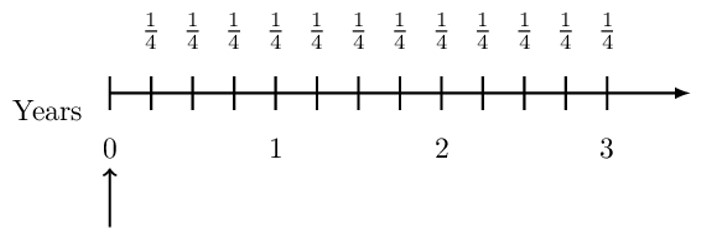
Therefore, the present value of the payments is given by:

$$ \text{PV}=\frac{1}{4}\text{v}^\frac{1}{4}+\frac{1}{4}\text{v}^\frac{1}{2}+\frac{1}{4}\text{v}^\frac{3}{4}+\cdots+\frac{1}{4}\text{v}^3 $$

Recognizing that the above expression is a sum of the finite geometric equation, we use the formula:

$$ \text{S}_\text{n}=\frac{\text{a}(1-\text{r}^\text{n})}{1-\text{r}} $$

Where a is the first term, r is the common ratio, and n is the number of terms. In this case, we have:

$$ \text{n}=12 \\ \text{r}=\frac{\frac{1}{4}\text{v}^\frac{1}{2}}{\frac{1}{4}\text{v}^\frac{1}{4}}=\text{v}^\frac{1}{4} $$

And

$$ \text{a}=\frac{1}{4}\text{v}^\frac{1}{4} $$

So,

$$ \text{PV}=\frac{1}{4}.\frac{\text{v}^\frac{1}{4}(1-\text{v}^{\frac{1}{4}\times12})}{1-\text{v}^\frac{1}{4}}=\frac{1}{4}.\frac{\text{v}^\frac{1}{4}(1-\text{v}^3)}{\text{v}^\frac{1}{4}\left(\frac{1}{\text{v}^\frac{1}{4}}-1\right)}=\frac{1-\text{v}^3}{4[\left(1+i\right)^\frac{1}{4}-1]} \\ =\frac{1-\text{v}^3}{\text i^{\left(4\right)}}{=\text{a}}_{\overline{3|}\text{i}}^{\left(4\right)} $$

Accumulation of Annuity-Immediate Payable Annually

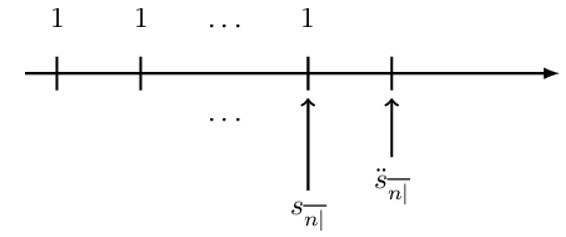
This is basically the value of a basic level annuity immediately after the last payment. More specifically, it is the value of a basic level annuity immediate at the annuity end date. It is denoted by \( \text{s}_{\overline{\text{n}}|\text{i}} \) read as “s, angle n at rate i,” where i is the periodic effective interest rate where the period matches the period of the payments. \( \textbf{s}_{\overline{\textbf{n}}|\textbf{i}} \) is illustrated by the following figure:

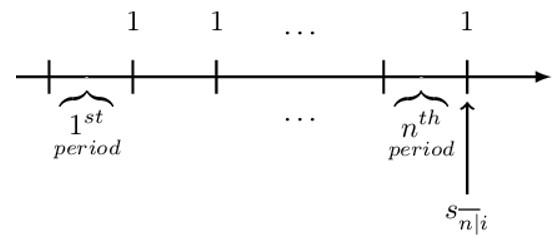
$$ \begin{align*} \text{s}_{\overline{\text{n}}|}&=\left(1+\text{i}\right)^{\text{n}-1}+\left(1+\text{i}\right)^{\text{n}-2}+\dots+1 \\ &=\left(1+\text{i}\right)^{\text{n}}\left[\left(1+\text{i}\right)^{-1}+\left(1+\text{i}\right)^{-2}+\dots\left(1+\text{i}\right)^{-\text{n}}\right] \\ &=\left(1+\text{i}\right)^{\text{n}}[\text{v}^{-1}+\text{v}^{-2}+\ldots\ \text{v}^{-\text{n}}] \\ &={\left(1+\text{i}\right)}^{\text{n}}\text{a}_{\overline{\text{n}|}} \\ &{=\left(1+\text{i}\right)}^{\text{n}}\left(\frac{1-\text{v}^\text{n}}{\text{i}}\right) \\ &=\frac{\left(1+\text{i}\right)^{\text{n}}-1}{\text{i}} \end{align*} $$

So,

$$ \text{s}_{\overline{\text{n}}|}=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{i}} $$

In the example above, if we want to find the accumulation of the present values at the last payment, then

$$ \begin{align*} \text{s}_{\overline{\text{n}}|}&=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{i}} \\ 1000\text{s}_{5\ \overline|}&=1000\times\frac{1.1^5-1}{0.1} \\ &=1000\times6.1051=6105.1\ \text{dollar} {\textbf{s}} \end{align*} $$

It is easy to see that:

$$ \text{s}_{\overline{\text{n}|}}=\text{a}_{\overline{\text{n}|}}\cdot {(1+\text{i})}^\text{n} $$

Where i is the period effective interest rate that matches the payment period.

Equivalently,

$$ \text{a}_{\overline{\text{n}}|}=\text{v}^\text{n}\text{s}_{\overline{\text{n}}|} $$

Where v is a periodic discount factor that matches the payment period.

Accumulation of Annuity-Immediate Payable m-thly

Consider a series of 1 unit payments paid in installments of \( \frac{1}{\text{m}} \), paid at the end of each mth period in the interval [0,n]. Then, the formula is quite straight forward. It is given by:

$$ \begin{align*} \text{s}_{\overline{\text{n}}|}^{(\text{m})} &=\left(1+\text{i}\right)^\text{n}(\text{a}_{\overline{\text{n}}|}^{\left(\text{m}\right)}) \\ &={\left(1+\text{i}\right)}^\text{n}\left(\frac{\text{i}}{\text{i}^\text{m}}\text{a}_{\overline{\text{n}}|}\right)=\frac{\text{i}}{\text{i}^\text{m}}\left[\left(1+\text{i}\right)^\text{n}.\text{a}_{\overline{\text{n}}|}\right] \\ &=\frac{\text{i}}{\text{i}^{(\text{m})}}\text{s}_{\overline{\text{n}}|}=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{i}^{(\text{m})}} \end{align*} $$

So,

$$ \text{s}_{\overline{\text{n}}|}^{(\text{m})}=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{i}^{(\text{m})}} $$

Computation of these annuities is quite straightforward in that; you have to know the conversion of effective interest rates to nominal rates.

Example: Accumulation of Annuity Immediate Payable m-thly

Represent symbolically, using upper m notation, and give the closed rule formula for the value of a 10-year annuity that pays 500 every month using a valuation date that is immediately after the final payment.

Solution

Since the valuation date is immediately after the final payment, we are asked to represent the accumulated value of an annuity immediate symbolically.

The payments are monthly, m=12. Denoting the accumulated value of the annuity by AV, then: 

$$ \text{AV}=\text{R}\cdot \text{s}_{\overline{10|}\text{i}}^{(12)} $$

Note that R is the annualized payment amount, and i is the effective interest rate so that from the information given in the question, we have:

$$ \text{AV}=500\times{12}\cdot \text{s}_{\overline{10|}\text{i}}^{(12)} \\ =6000.\text{s}_{\overline{10|}\text{i}}^{\left(12\right)} $$

Where

$$ \text{s}_{\overline{10|}\text{i}}^{(12)}=\frac{{(1+\text{i})}^{10}-1}{\text{i}^{(12)}} \\ \therefore \text{AV}=6000\cdot \frac{{(1+\text{i})}^{10}-1}{\text{i}^{(12)}} $$

Annuity-Due Paid Annually (Payments Made in Advance)

Consider a series of n payments made at the beginning of each period; that is, the first payment is made at time zero and the last payment at time n-1. It is represented by the symbol, \( {\ddot{\text{a}}}_{\overline{\text{n}}|\text{i}} \), is read as “a double dot, angle n at rate i” and defined as the value of a basic level annuity due at the annuity start date (or equivalently the value of a basic level annuity immediately before the first payment). The following timeline illustrates the basic annuity due:

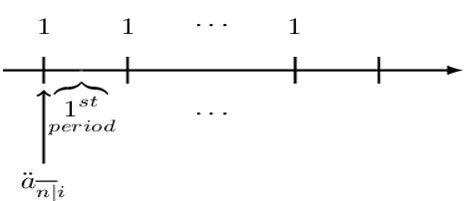
\( {\ddot{\text{a}}}_{\overline{\text{n}}|}\)is the present value of all the payments algebraically represented as:

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}=1+\text{v}^1+\text{v}^2+\dots+\text{v}^{\text{n}-1} $$

The expression above is a finite geometric sum with the common ratio v. Recall that the sum of a finite geometric sum is given by:

$$ S_n=\frac{\text{first term}-\text{first omitted term}}{1-\text{ratio}}$$

So in our case above, it must be true that:

$${\ddot{\text{a}}}_{\overline{\text{n}}|}=\frac{1-\text v^{\text n}}{1-\text v} $$

But \(d=1-v\) so that:

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}=\frac{1-\text{v}^\text{n}}{\text{d}}\ \ $$

The formula above is termed as a closed rule for the annuity due valuation.

Example: Basic Annuity Immediate

Calculate the present value of a series of payments of 1000 dollars payable at the beginning of each year from 2000 to 2010, assuming a 6% effective rate of interest.

Solution

$$ \begin{align*} {\ddot{\text{a}}}_{\overline{\text{n}}|}&=\frac{1-\text{v}^\text{n}}{\text{d}} \text{ where } \text{ d}=\frac{\text{i}}{1+\text{i}} \text{ and } \text{ v}=\frac{1}{1+\text{i}} \\ \Rightarrow 1000{\ddot{\text{a}}}_{\overline{10}|} & =1000\times\frac{1-1.06^{-10}}{\frac{0.06}{1.06}}\\ &=1000\times7.80169=7801.69 \end{align*} $$

(Note that you could have easily used the financial calculator here.)

It is also true that:

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}=1+\text{a}_{\overline{\text{n}-1}|} $$

which can be derived by general reasoning or algebraically. Moreover, it is easy to see that:

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}=(1+\text{i})\text{a}_{\overline{\text{n}}|} $$

Where i is the periodic effective interest rate that matches the payment period.

This can be seen by reasoning that \({\ddot{\text{a}}}_{\overline{\text{n}}|} \) and \(\text{a}_{\overline{\text{n}}|}\) are just single values which are one period apart as shown by the diagram below:

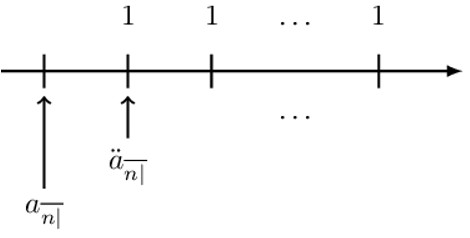
Therefore, if we had \(\text{a}_{\overline{\text{n}}|} \) and we wished to calculate \({\ddot{\text{a}}}_{\overline{\text{n}}|} \), we will need to accumulate \(\text{a}_{\overline{\text{n}}|} \) one period forward. Equivalently, we can write:

$$ \text{a}_{\overline{\text{n}}|}={\ddot{\text{a}}}_{\overline{\text{n}}|}.\text{v} $$

Where v is the periodic discount factor (pdf) that matches the payment period.

We can also illustrate the basic relationship between a ̈ \({\ddot{\text{a}}}_{\overline{\text{n}}|} \) and \( {\ddot{\text{s}}}_{\overline{\text{n}}|} \). Consider the following diagram:

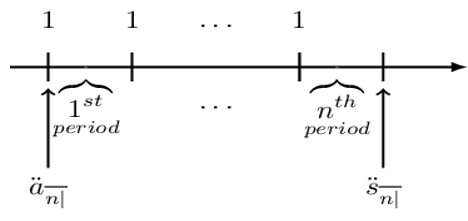
It is easy to see that

$$ {\ddot{\text{s}}}_{\overline{\text{n}|}}={\ddot{\text{a}}}_{\overline{\text{n}|}}\cdot {(1+\text{i})}^\text{n} $$

Where i is the periodic effective interest rate matching with the payment period. Equivalently,

$$ {\ddot{\text{a}}}_{\overline{\text{n}|}}={\ddot{\text{s}}}_{\overline{\text{n}|}}\cdot \text{v}^\text{n} $$

Where v is the periodic discount factor that matches the payment period.

Annuity-Due Payable m-thly

Consider the present value of a level annuity-due payable m-thly at a rate of 1 per unit time over an interval \( \left[0,\text{n}\right] \) in installments of \(\frac{1}{\text{m}}\) at the beginning of each pth time.

That is, a series of payments of an amount \(\frac{\text{d}^{\left(\text{m}\right)}}{\text{m}} \) in advance. This implies that:

$$ \begin{align*} {\ddot{\text{a}}}_{\overline{\text{n}}|}^{\left(\text{m}\right)} & =\frac{\text{i}}{\text{d}^{\left(\text{m}\right)}}\text{a}_{\overline{\text{n}}|}=\frac{\text{i}}{\text{d}^{\left(\text{m}\right)}}\left[\frac{1-\text{v}^\text{n}}{\text{i}}\right] \\ & =\frac{1-\text{v}^\text{n}}{\text{d}^{(\text{m})}} \end{align*} $$

So,

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}^{\left(\text{m}\right)}=\frac{1-\text{v}^\text{n}}{\text{d}^{(\text{m})}} $$

where

$$ \text{d}^{(\text{m})}=\text{m}\left[1-\left(1+\text{i}\right)^{-\left(\frac{1}{\text{m}}\right)}\right] $$

Also,

$$ \text{a}_{\overline{\text{n}}|}^{(\text{m})}=\text{v}^\frac{1}{\text{m}}{\ddot{\text{a}}}_{\overline{\text{n}}|}^{\left(\text{m}\right)} $$

Which can be algebraically proven to be equal to:

$$ \frac{1-\text{v}^\text{n}}{\text{d}^{(\text{m})}} $$

Example: Annuity Due Payable m-thly

Consider a 3-year annuity due paying 1 per year. The payments are made semi-annually, the first payment made at the beginning of the first half. We need to find a closed rule expression for this annuity.

Solution

Consider the following diagram:

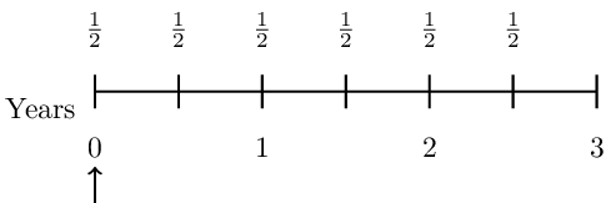
Therefore, the present value of the annuity is given by:

$$ \text{PV}=\frac{1}{2}+\frac{1}{2}\text{v}^\frac{1}{2}+\frac{1}{2}\text{v}+\frac{1}{2}\text{v}^\frac{3}{2}+\frac{1}{2}\text{v}^2+\frac{1}{2}\text{v}^\frac{5}{2} $$

Using the formula of the geometric sum given by:

$$ \begin{align*} \text{V}\text{alue of Geometric Sum} & =\frac{\text{a}_1(1-\text{r}^\text{n})}{1-\text{r}} \\ & =\frac{\frac{1}{2}\left(1-\text{v}^{6\times\frac{1}{2}}\right)}{1-\text{v}^\frac{1}{2}}=\frac{1-\text{v}^3}{2(1-\text{v}^\frac{1}{2})\ }=\frac{1-\text{v}^3}{\text{d}^{(2)}}={\ddot{\text{a}}}_{\overline{3|}\text{i}}^{\left(2\right)} \end{align*} $$

Note that we have used the relationship that:

$$ 1-\text{d}=\left(1-\frac{\text{d}^{(\text{m})}}{\text{m}}\right)^\text{m} \\ \Rightarrow\ \text{d}^{(\text{m})}=\text{m}\left[1-\left(1-\text{d}\right)^\frac{1}{\text{m}}\right] $$

But \(1-d=v\)

$$ \therefore \text{d}^{(\text{m})}=\text{m}\left[1-\text{v}^\frac{1}{\text{m}}\right] $$

Accumulation of Annuity-due Payable Annually

The value of a basic level annuity, one (payment) period after the last payment is denoted by \({\ddot{\textbf{s}}}_{\overline{\textbf{n}}|\textbf{i}}\) and read as “s, double dot, angle n at a rate i. “ i is the periodic effective interest rate where the period matches the period of the payment. More specifically, \({\ddot{\textbf{s}}}_{\overline{\textbf{n}}|\textbf{i}}\) is defined as the accumulated value of a basic level annuity due. It isillustrated as follows:

$$ \begin{align*} {\ddot{\text{s}}}_{\overline{\text{n}}|}&=\left(1+\text{i}\right)^\text{n}+\left(1+\text{i}\right)^{\text{n}-1}+\dots+(1+\text{i}) \\ &=\left(1+\text{i}\right)^\text{n}\left[1+\left(1+\text{i}\right)^{-1}+\left(1+\text{i}\right)^{-2}+\dots+\left(1+\text{i}\right)^{1-\text{n}}\right] \\ &=\left(1+\text{i}\right)^\text{n}\left[1+\text{v}^{-1}+\text{v}^{-2}+\dots+\text{v}^{1-\text{n}}\right] \end{align*} $$

The expression in the square brackets is the present value of the annuity due. That is:

$$ {\ddot{\text{a}}}_{\overline{\text{n}}|}=1+\text{v}^{-1}+\text{v}^{-2}+\dots+\text{v}^{1-\text{n}} $$

So,

$$ \begin{align*} {\ddot{\text{s}}}_{\overline{\text{n}}|}&=\left(1+\text{i}\right)^\text{n}{\ddot{\text{a}}}_{\overline{\text{n}}|}=\left(1+\text{i}\right)^\text{n}\left[\frac{1-\text{v}^\text{n}}{\text{d}}\right] \\ &=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{d}} \end{align*} $$

So,

$$ {\ddot{\text{s}}}_{\overline{\text{n}}|}=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{d}}\ $$

Also, notice that

$$ \text{s}_{ \overline{ \text{n}+1 }| }={\ddot{\text{s}}}_{\overline{\text{n}}|}+1 $$

We can illustrate the relationship between \({\ddot{\text{s}}}_{\overline{\text{n}}|} \) and \(\text{s}_{\overline{\text{n}}|}\). Consider the following diagram:

We can see clearly see that:

$$ {\ddot{\text{s}}}_{\overline{\text{n}}|}=\text{s}_{\overline{\text{n}}|}.(1+\text{i}) $$

Where i is the periodic effective interest rate that matches the payment period.

This is true because we need to accumulate \( \text{s}_{\overline{\text{n}}|}\) one period forward to get \({\ddot{\text{s}}}_{\overline{\text{n}}|}\). Equivalently,

$$ \text{s}_{\overline{\text{n}}|}={\ddot{\text{s}}}_{\overline{\text{n}}|}.\text{v} $$

Where v is the periodic discount factor that matches the payment period.

Accumulation of Annuity-Due payable m-thly

Consider a series of payment of 1 paid in installments of \(\frac{1}{\text{m}}\) at the beginning of each mth period, the accumulation is given by:

$$ \begin{align*} {\ddot{\text{s}}}_{\overline{\text{n}}|}^{(\text{m})}&=\left(1+\text{i}\right)^\text{n}({\ddot{\text{a}}}_{\overline{\text{n}}|}^{\left(\text{m}\right)}) \\ &=\left(1+\text{i}\right)^\text{n}\left(\frac{\text{i}}{\text{d}^{\left(\text{m}\right)}}\text{a}_{\overline{\text{n}}|}\right) \\ &=\frac{\text{i}}{\text{d}^{\left(\text{m}\right)}}\left[\left(1+\text{i}\right)^\text{n}.\text{a}_{\overline{\text{n}}|}\right]=\frac{\text{i}}{\text{d}^{\left(\text{m}\right)}}\text{s}_{\overline{\text{n}}|} \\ &=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{d}^{(\text{m})}} \end{align*} $$

So,

$$ {\ddot{\text{s}}}_{\overline{\text{n}}|}^{(\text{m})}=\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{d}^{(\text{m})}} $$

Continuously Payable Annuities

Assume that n is a non-negative number, the present value of the continuously payable annuity at the rate of 1 is denoted by \( {\overline{\textbf{a}}}_{\overline{\textbf{n}}|}\)(pronounced as “a bar n”).

Intuitively,

$$ \begin{align*} {\overline{\text{a}}}_{\overline{\text{n}}|}&=\int_{0}^{\text{n}}{1.\text{v}^\text{t}\text{dt}=\int_{0}^{\text{n}}{1.\text{e}^{-\delta \text{t}}\text{dt}=\left[-\frac{1}{\delta}\text{e}^{-\delta \text{t}}\right]\begin{matrix}\text{n}\\0\\\end{matrix}}} \\ &=\frac{1-\text{e}^{-\text{n}\delta}}{\delta}=\frac{1-\text{v}^\text{n}}{\delta}\ \ where\ \delta=\text{ln}(1+\text{i}) \end{align*} $$

So,

$$ {\overline{\text{a}}}_{\overline{\text{n}}|}=\frac{1-\text{v}^\text{n}}{\delta}\ \forall\ \delta\ \neq0 \text{ non-integral values of } \text{n} $$

Therefore, \({\overline{\text{a}}}_{\overline{\text{n}}|} \) is the present value of the n-year continuous annuity paying 1 per year.

Given that \(\frac{1-\text{v}^\text{n}}{\delta}\) can be written as:

$$ \frac{\text{i}}{\delta}\left(\frac{1-\text{v}^\text{n}}{\text{i}}\right) $$

It immediately follows that:

$$ {\overline{\text{a}}}_{\overline{\text{n}}|}=\frac{\text{i}}{\delta}\text{a}_{\overline{\text{n}}|} $$

This relationship is very useful when it comes to using actuarial tables because\({\overline{\text{a}}}_{\overline{\text{n}}|} \) is not tabulated while \(\text{a}_{\overline{\text{n}}|}\) and \(\frac{\text{i}}{\delta}\) is tabulated.

Example: Continuously Payable Annuity

Compute an approximate value for the future value of a series of payments of 100 dollars each payable for 1 year at the beginning of each week, taking an effective rate to be 8% per annum.

Solution

Assuming that there are 52.18 weeks in a year, we can approximate weekly payments to be continuous payments. Thus,

$$ \begin{align*} 52.18\times100\text{a}_{\overline{1}|}^{@8\%}&=5218\times\frac{1-\text{v}}{\delta} \\ &=5218\times\frac{1-0.92593}{0.076961}=5021.99. \end{align*} $$

Accumulation of a Continuously Payable Annuity

The accumulated amount of a continuously payable annuity when the payments cease is denoted by \({\overline{\text{s}}}_{\overline{\text{n}}|} \) and defined by:

$$ \begin{align*} {\overline{\text{s}}}_{\overline{\text{n}}|}&=\left(1+\text{i}\right)^\text{n}({\overline{\text{a}}}_{\overline{\text{n}}|}) \\ &=\frac{\left(1+\text{i}\right)^\text{n}-1}{\delta}=\frac{\text{i}}{\delta}\ \left(\frac{\left(1+\text{i}\right)^\text{n}-1}{\text{i}}\right)=\frac{\text{i}}{\delta}\text{s}_{\overline{\text{n}}|} \\ \therefore{\overline{\text{s}}}_{\overline{\text{n}}|} & =\frac{\left(1+\text{i}\right)^\text{n}-1}{\delta}=\frac{\text{i}}{\delta}\text{s}_{\overline{\text{n}}|} \end{align*} $$

Similarly, we can note that:

$$ \begin{align*} {\overline{\text{s}}}_{\overline{\text{n}}|}&={\overline{\text{a}}}_{\overline{\text{n}}|}\cdot \left(1+\text{i}\right)^\text{n}=\int_{0}^{\text{n}}{{(1+\text{i})}^{\text{n}-\text{t}}\text{dt}=\int_{0}^{\text{n}}{\text{e}^{\delta(\text{n}-\text{t})}\text{dt}}} \\ &=\frac{\left(1+\text{i}\right)^\text{n}-1}{\delta} \end{align*} $$

Which is the closed rule formula for a continuously paid annuity.

In the example above, the accumulated value when the payments terminate will be:

$$ {\overline{\text{s}}}_{\overline{1}|}=52.18\times100\times\left[\frac{\left[\left(1.08\right)^1-1\right)}{\text{ln} \left(1.08\right)}\right]=5424.043 $$

Perpetuities

Consider an annuity payable forever, which is consequently called a perpetuity. We shall consider basic perpetuity immediate and due.

Basic Perpetuity Immediate

The following timeline illustrates basic perpetuity immediate:

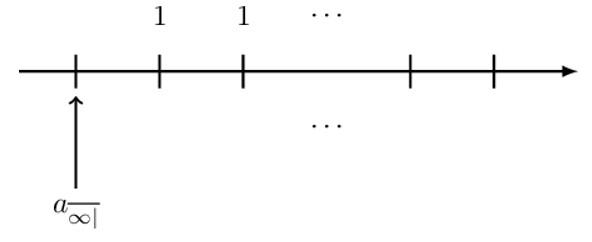
Therefore, the present value of the perpetuity immediate is given by:

$$ \text{a}_{\overline{\infty|}}=\text{v}+\text{v}^2+\text{v}^3+\dots $$

Using infinite geometric progression,

$$ \begin{align*} \sum_{\text{i}=1}^{\infty}{\text{ax}^\text{i}}&=\text{ax}+\text{ax}^2+\text{ax}^3+\dots=\frac{\text{a}}{1-\text{x}} \\ &\Rightarrow \text{v}+\text{v}^2+\text{v}^3+\dots=\frac{\text{v}}{1-\text{v}}=\frac{\text{v}\left(1\right)}{\text{v}\left(\frac{1}{\text{v}}-1\right)}=\frac{1}{\text{i}} \end{align*} $$

Alternatively, we can view this as follows:

We know that the present value of payments of 1 per annum payable at the end of each year for n years is:

$$ \text{a}_{\overline{\text{n}|}}=\frac{1-\text{v}^\text{n}}{\text{i}} $$

Now let \( \text{n}\rightarrow\infty \), i.e.,

$$ \underset { \text{n}\rightarrow \infty }{ \text{lim} } {\frac{1-\text{v}^\text{n}}{\text{i}}}=\frac{1}{\text{i}} $$

Therefore,

$$ \text{a}_{\overline{\infty}|}=\frac{1}{\text{i}} $$

Basic Perpetuity Due

The basic perpetuity due is illustrated below:

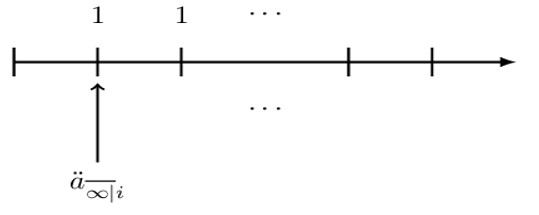So, the perpetuity due is given by:

$$ {\ddot{\text{a}}}_{\overline{\infty}|}=1+\text{v}+\text{v}^2+\dots $$

Similarly, the present value of payments of 1 per annum payable at the beginning of each year for n years is:

$$ \frac{1-\text{v}^\text{n}}{\text{d}} $$

Now let \(\text{n}\rightarrow\infty \), i.e.,

$$ \begin{align*} \underset { \text{n}\rightarrow \infty }{ \text{lim} }{\frac{1-\text{v}^\text{n}}{\text{d}}}&=\frac{1}{\text{d}} \\ \therefore{\ddot{\text{a}}}_{\overline{\infty}|}&=\frac{1}{\text{d}} \end{align*} $$

Example: Perpetuity immediate

An annuity pays 1500 dollars annually in arrears without termination. Using an annual effective interest of 8%, calculate the present value.

Solution

$$ {\text{a}}_{\overline{\infty}|}=\frac{1}{\text{i}}\ \ \Rightarrow 1500\text{a}_{\overline{\infty}|}=\frac{1500}{0.08}=18750 \text{ dollars} $$

The following diagram illustrates the relationship between the annuities and their accumulations:

1.5. Deferred Annuities

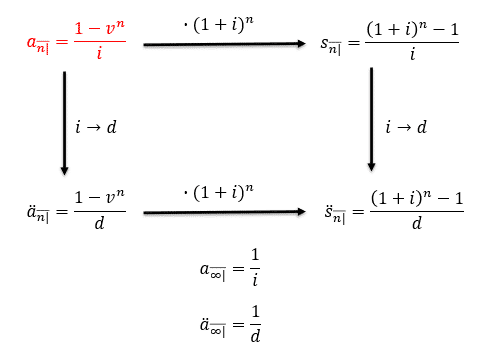
A deferred annuity is a type of annuity where there is no payment made during the first period. In other words, payments are made some other time.

Deferred Annuity Immediate

Let m and n be non-negative integers, then the present value of series of n payments each of amount 1 due at \(\left(\text{m}+1\right),\left(\text{m}+2\right),\dots,\ (\text{m}+\text{n})\) is denoted by \(\text{m}|\text{a}_{\overline{\text{n}}|} \) and referred to as deferred annuity immediate. It is defined as:

$$ \begin{align*} \text{m}|\text{a}_{\overline{\text{n}}|}&=\text{v}^{\text{m}+1}+\text{v}^{\text{m}+2}+\dots+\text{v}^{\text{m}+\text{n}} \\ &=\left(\text{v}+\text{v}^2+\text{v}^3+\dots+\text{v}^{\text{m}+\text{n}}\right)-\left(\text{v}+\text{v}^2+\text{v}^3+\dots \text{v}^\text{m}\right) \\ &=\text{a}_{\overline{\text{m+n}}|}-\text{a}_{\overline{\text{n}}|} \end{align*} $$

Note also that:

$$ \begin{align*} \text{m}|\text{a}_{\overline{\text{n}}|}&=\text{v}^{\text{m}+1}+\text{v}^{\text{m}+2}+\dots+\text{v}^{\text{m}+\text{n}} \\ &=\text{v}^\text{m}\left(\text{v}+\text{v}^2+\text{v}^3+\dots \text{v}^\text{n}\right) \\ &=\text{v}^\text{m}\text{a}_{\overline{\text{n}}|} \end{align*} $$

Therefore,

$$ \text{m}|\text{a}_{\overline{\text{n}}|}=\text{a}_{\overline{\text{m}+\text{n}}|}-\text{a}_{\overline{\text{n}}|} $$

And

$$ \text{m}|\text{a}_{\overline{\text{n}}|}=\text{v}^\text{m}\text{a}_{\overline{\text{n}}|} $$

Either of these equations might be used to evaluate the deferred annuity.

Deferred Annuity Due

Using similar arguments, we can define deferred annuity due as follows:

$$ \text{m}|{\ddot{\text{a}}}_{\overline{\text{n}}|}=\text{v}^\text{m}{\ddot{\text{a}}}_{\overline{\text{n}}|} $$

Continuously Payable Deferred Annuities

Given that m is non-negative, a continuously payable deferred annuity is denoted by \( {\textbf{m}}|{\overline{\textbf{a}}}_{\overline{\textbf{n}}|}.. \) It is a representation of value at time 0 of a continuously payable annuity of 1 per unit, which is paid at time m units. Mathematically,

$$ \begin{align*} \text{m}|{\overline{\text{a}}}_{\overline{\text{n}}|} &=\int_{\text{m}}^{\text{m}+\text{n}}{\text{e}^{-\delta \text{t}}\text{dt}} \\ &=\text{e}^{-\delta \text{m}}\int_{0}^{\text{n}}{\text{e}^{-\delta \text{s}}\text{ds}=\int_{0}^{\text{m}+\text{n}}{\text{e}^{-\delta \text{t}}\text{dt}}}-\int_{0}^{\text{m}}{\text{e}^{-\delta \text{t}}\text{dt}} \\ \Rightarrow \text{m}|{\overline{\text{a}}}_{\overline{\text{n}}|} & ={\overline{\text{a}}}_{\overline{\text{m}+\text{n}}|}-{\overline{\text{a}}}_{\overline{\text{n}}|} \\ &=\text{v}^\text{m}{\overline{\text{a}}}_{\overline{\text{n}}|} \end{align*} $$

Deferred Annuity Payable m-thly

The present value of the annuity due and immediate payable m-thly at a rate of 1 per unit time in n times and deferred for time m units are given by:

$$ \text{m}|\text{a}_{\overline{\text{n}}|}^{(\text{m})}=\text{v}^\text{m}\text{a}_{\overline{\text{n}}|}^{(\text{m})} $$

and

$$ \text{m}|{\ddot{\text{a}}}_{\overline{\text{n}}|}^{(\text{m})}=\text{v}^\text{m}{\ddot{\text{a}}}_{\overline{\text{n}}|}^{(\text{m})} $$

Symbolic Examples of Level Annuities

In this section, we will discuss some of the symbolic examples built from level annuities we have been discussing above. These should build a concrete foundation in understanding annuity symbols.

Example 1: Symbolic Representation

Symbolically represent the value of the annuity shown at the valuation date shown.

Solution

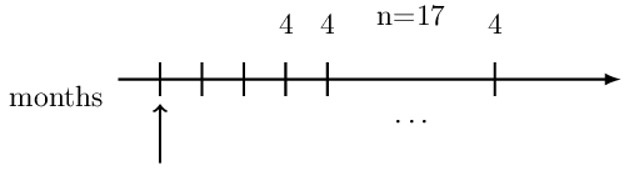
Notice the timeline above illustrates 17 monthly payments of 4. At the valuation date shown, we do not have a definite symbol that we could use since the payments are monthly, and the first payment is made after three periods (months) from the valuation date.

To represent the valuation, we need to choose an intermediate payment period. Now, if we choose one month before the first payment (shown by the dotted arrow), we would have a definite symbol (annuity immediate).

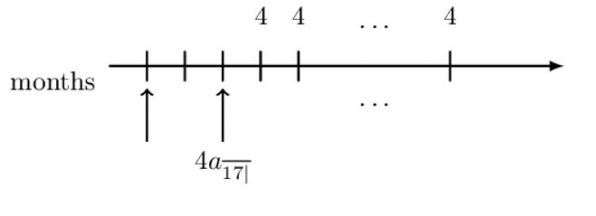The present value of the monthly payments at the chosen intermediate date is:

$$ {4\text{a}}_{\overline{17|}} $$

However, we need to discount (by two periods) this value to our desired valuation date, so we have:

$$ \text{V}={4\text{a}}_{\overline{17|}}.\text{v}^2 $$

But from the definition deferred annuity immediate, we know that:

$$ \text{m}|\text{a}_{\overline{\text{n}}|}=\text{v}^\text{m}\text{a}_{\overline{\text{n}}|} $$

Therefore

$$ \text{V}={4\text{a}}_{\overline{17|}}.\text{v}^2={4}\times{2}|\text{a}_{\overline{\text{17}}|} $$

Alternatively, if we choose the intermediate valuation date to be at the time of the first payment (as shown in the diagram below), then we would have an annuity due.

Hence, we can use the symbols we have been discussing.

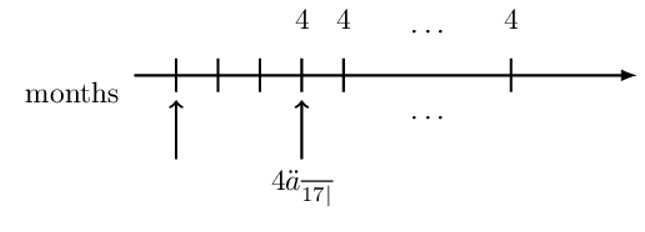The present value of the monthly payments at the chosen intermediate date is:

$$ {4\ddot{\text{a}}}_{\overline{17|}} $$

However, we need to discount (by three periods) this value to our desired valuation date, so we have:

$$ \text{V}={4\ddot{\text{a}}}_{\overline{17|}}.\text{v}^3 $$

Now using the definition of deferred annuity we have:

$$ \text{V}={4\ddot{\text{a}}}_{\overline{17|}}.\text{v}^3=4\left(3|{\ddot{\text{a}}}_{\overline{17|}}\right) $$

Example 2: Symbolic Representation

Symbolically represent the value of the perpetuity shown at the valuation date shown.

Solution

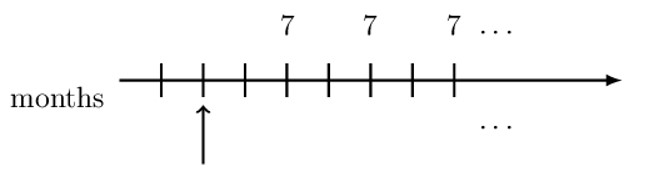
Note that the timeline represents the quarterly payments of 7 forever (perpetuity). Also, the valuation date is two months before the first payment. Since we are dealing with quarterly payments, we will work with a quarterly effective interest rate.

Since we do not have a symbol to represent the value of the perpetuity at the valuation date, we will use an intermediate valuation date. Let us take the intermediate valuation date to be at the time of the first payment so that we have “perpetuity due.” Consider the following diagram:

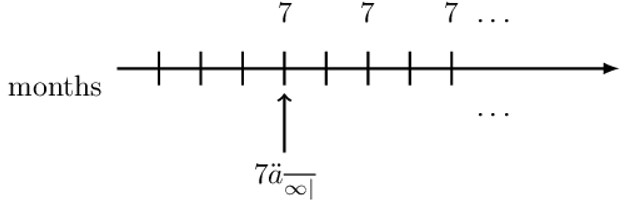
So at the intermediate valuation date, the value of the perpetuity is \( {7\ddot{\text{a}}}_{\overline{\infty|}\text{q}}\) where q is the quarterly effective rate of interest. To get the value of the perpetuity at our desired valuation date (shown by solid upward arrow), we will need to discount \({7\ddot{\text{a}}}_{\overline{\infty|}\text{q}}\) back by two months using the monthly effective interest rate m. That is:

$$ \text{V}={7\ddot{\text{a}}}_{\overline{\infty|}\text{q}}\cdot \ \text{v}_\text{m}^2 $$

Example 3: Symbolic Representation

Symbolically represent the value of the annuity shown at the valuation date shown.

Solution

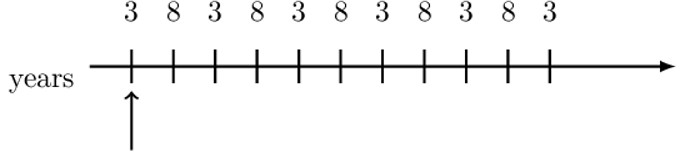
Note that the timeline is in years so that we have non-level yearly payments but with some kind of pattern. Since we have chosen our valuation date to be at the first payment, a natural thing to do is split the payments as follows:

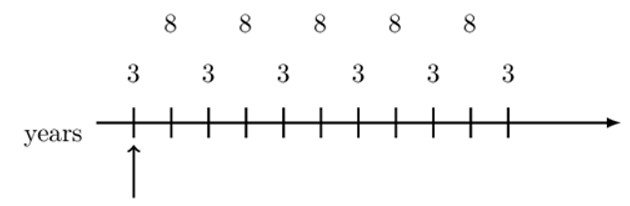
Therefore, the value of the annuity at the chosen valuation date is equivalent to the present value of each annuity . That is:

$$ \begin{align*} \text{V}&=3{\ddot{\text{a}}}_{\overline{6|}\text{b}}+8{\ddot{\text{a}}}_{\overline{5|}\text{b}}\cdot \text{v}_\text{a} \\ &=3{\ddot{\text{a}}}_{\overline{6|}\text{b}}+8\text{a}_{\overline{5|}\text{b}}\cdot (1+\text{a}) \end{align*} $$

Where a is the annual effective interest rate, and b is the biannual interest rate.

Alternatively, we can arrange the payments as follows:

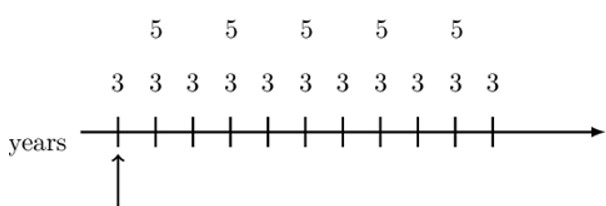
So the value of the annuity is given by:

$$ \begin{align*} \text{V}&=3{\ddot{\text{a}}}_{\overline{11|}\text{a}}+5{\ddot{\text{a}}}_{\overline{5|}\text{b}}\cdot \text{v}_\text{a} \\ &=3{\ddot{\text{a}}}_{\overline{11|}\text{a}}+5\text{a}_{\overline{5|}\text{b}}\cdot (1+\text{a}) \end{align*} $$

Where a is the annual effective interest rate, and b is the biannual interest rate.

Example 4: Symbolic Representation

Symbolically represent the value of the annuity shown at the valuation date shown

Solution

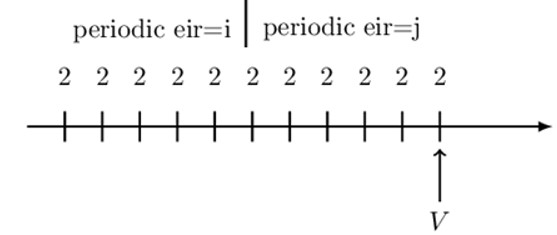
Notice that we have 11 level payments of 2 where the periodic effective interest changes from i to j at the sixth payment. We need to use the period at which the periodic interest rate changes as the intermediate valuation date. Consider the following timeline:

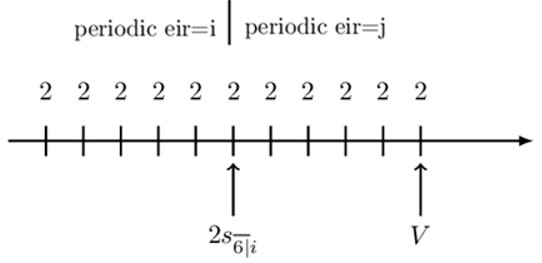
Therefore, the value of the annuity at the chosen valuation date is given by:

$$ \text{V}=2\text{s}_{\overline{6|}\text{i}}\cdot \left(1+\text{j}\right)^5+2\text{s}_{\overline{5|}\text{j}} $$

Alternatively, consider the following arrangement:

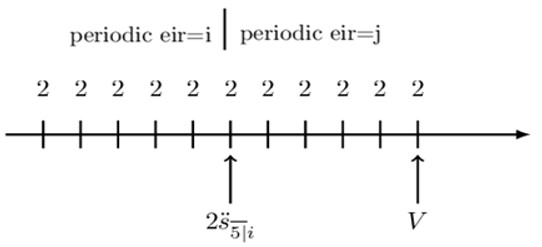
Therefore the value of the annuity will be:

$$ \text{V}=2{\ddot{\text{s}}}_{\overline{5|}\text{i}}\cdot \left(1+\text{j}\right)^5+2\text{s}_{\overline{6|}\text{j}} $$

Example 5: Symbolic Representation

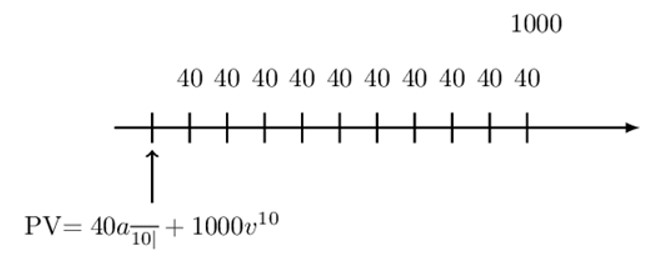
Draw the timeline, including the valuation datethat corresponds to the equation \( \text{PV}=40\text{a}_{\overline{10|}} +1000\text{v}^{10} \).

Solution

To answer this question effectively, look at the term that has an annuity symbol, in this case, \(40\text{a}_{\overline{10|}} \). That is, we have ten payments (annuity immediate) of 40 and a lump sum of 1000 at time ten. So the timeline of the payments is given by:

Example 6: Symbolic Representation

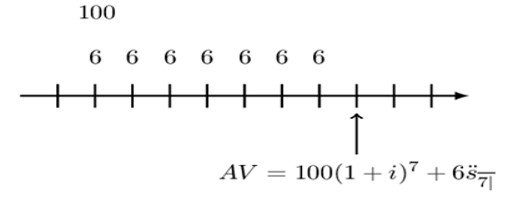
Draw the timeline, including the valuation date that corresponds to the following equation:

$$ \text{AV}=100{(1+\text{i})}^7+ 6{\ddot{\text{s}}}_{\overline{7|}} $$

Solution

Using the same analogy as in example 5, the timeline for the above payment is given by:

Non-Level Annuities

Geometric Annuities

Let n denote the number of payment periods, with a common ratio (1+r) and the first payment to be 1 unit. Then using the geometric progression formulation, the present value is given:

$$ \text{PV}=\text{v}+\text{v}^2\left(1+\text{r}\right)+\dots+\text{v}^\text{n}\left(1+\text{r}\right)^{\text{n}-1} $$

Note that the right-hand side of the equation above is the sum of finite geometric series. Therefore, we can use the formula:

$$ \text{S}_\text{n}=\frac{\text{a}_1\left(1-\text{r}^\text{n}\right)}{1-\text{r}} $$

Where

\(\text{a}_1\) = first term of the geometric series

\(\text{r}\) = percentage change in the subsequent payments.

\(\text{n}\) = number of terms

Then, for the geometric annuities, note that \(\ \text{v}=\frac{1}{1+\text{i}} \) so that

$$ \begin{align*} \text{PV}&=\text{v}\left[\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{1-\frac{1+\text{r}}{1+\text{i}}}\right]=\text{v}\left[\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\frac{\text{i}-\text{r}}{1+\text{i}}\ }\right] \\ &=\text{v}\left[\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\text{v}(i-\text{r})}\right]\\ \therefore\text{PV}&=\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\text{i}-\text{r}} \end{align*} $$

Example: Geometric Annuity

An annuity provides 20 annual payments where the first payment is 1000 dollars. The subsequent payments are such that it is 4% more than the preceding payment.

Calculate the present value of the payments at 7% effective interest.

Solution

$$ \begin{align*} \text{PV}&=\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\text{i}-\text{r}}\Rightarrow \text{PV}=1000\left[\frac{1-\left(\frac{1+0.04}{1+0.07}\right)^{20}}{0.07-0.04}\right] \\ &=1000\times14.459071=14459.071\ dollars \end{align*} $$

Alternatively, recall that a geometric annuity is an annuity in which the payments form a geometric progression. It illustrated by the following timeline:

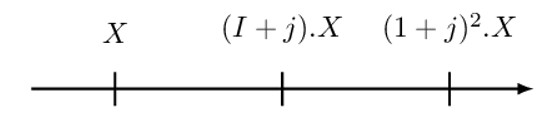
Note that the above timeline is a geometric annuity with a common ratio of (1+j). To value a geometric annuity, we follow a three-step process:

Step 1: Value each payment at the valuation date.

Step 2: Factor out the first term.

Step 3: Recognize the remaining factor as \({\ddot{\text{a}}}_{\overline{\text{n}|}} \text{ or } \text{s}_{\overline{\text{n}|}}\).

Example: Geometric Annuity

Consider a geometric annuity where the first payment is 10 with subsequent payments being 10% more than the preceding payments. What is the present value of the annuity immediately before the first payment if the periodic effective interest rate is 8%?

Solution

The timeline and the valuation date of the annuity are as shown below:

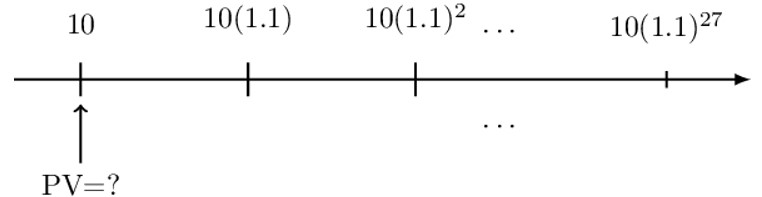
We shall follow the three-step process:

Step 1: Value each payment at the valuation date.

$$ \text{PV}=10+10\left(1.1\right)\text{v}+10{(1.1)}^2\text{v}^2\cdots+10{(1.1)}^{27}\text{v}^{27} $$

But

$$ \begin{align*} \text{v}&=\frac{1}{1.08} \\ &\Rightarrow\text{PV}=10+10\left(\frac{1.1}{1.08}\right)+10\left(\frac{1.1}{1.08} \right)^2\cdots+10\left(\frac{1.1}{1.08}\right)^{27} \end{align*} $$

Step 2: Factor out the first term.

$$ \text{PV}=10\left[1+\left(\frac{1.1}{1.08}\right)+\left(\frac{1.1}{1.08}\ \right)^2\cdots+\left(\frac{1.1}{1.08}\right)^{27}\right] $$

Step 3: Recognize the remaining factor as \( {\ddot{\text{a}}}_{\overline{\text{n}|}} \text{ or } \text{s}_{\overline{\text{n}|}}\).

The expression in the square bracket is a sum of a finite geometric series (with 28 terms) with a common ratio of \( \text{r}=\frac{1.1}{1.08} \). Now since

$$ \text{r}=\frac{1.1}{1.08} > 1 $$

We can let

$$ \begin{align*} \frac{1.1}{1.08}&=1+\text{i} \\ \Rightarrow\ \text{i}&=0.0185 \end{align*} $$

And therefore,

$$ \begin{align*} \text{PV}&=10\left[1+\left(\frac{1.1}{1.08}\right)+\left(\frac{1.1}{1.08}\ \right)^2\cdots+\left(\frac{1.1}{1.08}\right)^{27}\right] \\ &=10\left[1+\left(1+\text{i}\right)+\left(1+\text{i} \right)^2\cdots+\left(1+\text{i}\right)^{27}\right] \\ \text{PV}&=10\cdot \text{s}_{\overline{28|}i=0.0185}=362.56 \end{align*} $$

Example: Geometric Annuity

Consider a geometric annuity where the first payment is 10 with subsequent payments being 10% more than the preceding payments.

What is the present value of the annuity immediately before the first payment if the periodic effective interest rate is 12%?

Solution

The timeline and the valuation date of the annuity are as shown below:

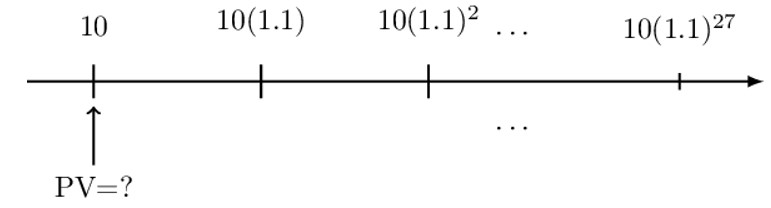
We shall follow the three-step process:

Step 1: Value each payment at the valuation date.

$$ \text{PV}=10+10\left(1.1\right)\text{v}+10{(1.1)}^2\text{v}^2\cdots+10{(1.1)}^{27}\text{v}^{27} $$

But

$$ \begin{align*} \text{v}&=\frac{1}{1.12}\\ \Rightarrow\text{PV}&=10+10\left(\frac{1.1}{1.12}\right)+10\left(\frac{1.1}{1.12}\ \right)^2\cdots+10\left(\frac{1.1}{1.12}\right)^{27} \end{align*} $$

Step 2: Factor out the first term.

$$ \text{PV}=10\left[1+\left(\frac{1.1}{1.12}\right)+\left(\frac{1.1}{1.12}\ \right)^2\cdots+\left(\frac{1.1}{1.12}\right)^{27}\right] $$

Step 3: Recognize the remaining factor as \({\ddot{\text{a}}}_{\overline{\text{n}|}} \text{ or } \text{s}_{\overline{\text{n}|}}\).

Notice that the expression in the square bracket is a sum of a finite geometric series (28 terms) with

$$ \text{r}=\frac{1.1}{1.12} $$

Now since

$$ \text{r}=\frac{1.1}{1.12} < 1 $$

We can let

$$ \begin{align*} \frac{1.1}{1.12}&=\frac{1}{1+\text{i}}=\text{v}^{\text{new}} \\ \Rightarrow\text{i}&=0.0182 \end{align*} $$

And

$$ \begin{align*} \text{PV} & =10\left[1+\text{v}+\text{v}\cdots+\text{v}^{27}\right] \\ \text{PV} & =10\cdot {\ddot{\text{a}}}_{\overline{28|}\text{i}}=221.83 \end{align*} $$

Example 1: Geometric Annuity (Unknown Interest Rate)

A 10-year annuity immediate with annual payments has an initial payment of 11. Each subsequent payment is 10% more than its preceding payment. The accumulated value of the annuity is 220.8 using an annual effective interest rate, i.

Determine i.

Solution

As a norm, we will start with the timeline:

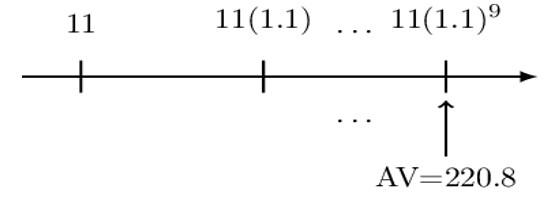
Again we will use the three-step process:

Step 1: Value each payment at the valuation date.

$$ \text{AV}=11{(1.1)}^9+11\left(1.1\right)^8(1+\text{i})+\cdots(10 \text{ terms}) $$

Step 2: Factor out the first term.

$$ 220.8=11{(1.1)}^9\cdot \left(1+\frac{1+\text{i}}{1.1}+\cdots(10 \text{ terms})\right) $$

Step 3: Recognize the remaining factor.

Note that if \( \frac{1+\text{i}}{1.1}>1 \) we use \( \text{s}_{\overline{10|}\text{j}}=\left(1+\frac{1+\text{i}}{1.1}+\cdots(10 \text{ terms})\right) \) where \(\text{j}=\frac{1+\text{i}}{1.1}-1 \). On the other hand, if \( \frac{1+\text{i}}{1.1}<1\) we use \( {\ddot{\text{a}}}_{\overline{10|}\text{j}}=\left(1+\frac{1+\text{i}}{1.1}+\cdots(10 \text{ terms})\right) \) where \( \text{j}=\frac{1.1}{1+\text{i}}-1 \). Now, note that \( \left(1+\frac{1+\text{i}}{1.1}+\cdots(10 \text{ terms})\right) < 10. \)since we must multiply it with \(11\left(1.1\right)^9(=25.93)\) to get 220.8. Therefore, \({\ddot{a}}_{\bar{10|}j}<10\ and\ s_{\bar{10|}j}>10.\) Therefore, we have that:

$$ 220.8=11{(1.1)}^9\cdot {\ddot{\text{a}}}_{\overline{10|}\text{j}} $$

Using a financial calculator we get:

$$ \begin{align*} \text{j}&=0.03773 \\ \Rightarrow 0.03773 & =\frac{1.1}{1+i}-1 \\ \therefore \text{i} & =0.06 \end{align*} $$

Example 2: Geometric Annuity (Unknown Interest Rate)

A 10-year annuity immediate with annual payments has an initial payment of 7. Each subsequent payment is 10% more than its preceding payment. The present value of the annuity is 70.49 using an annual effective interest rate, i.

Determine i.

Solution

As usual, we start with the number line:

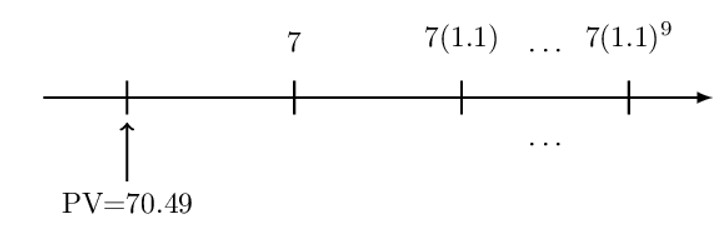
We apply the three-step process:

Step 1: Value each payment at the valuation date.

$$ \text{PV}=\frac{7}{1+\text{i}}+\frac{7(1.1)}{{(1+\text{i})}^2}+\cdots(10 \text{ terms} ) $$

Step 2: Factor out the first term.

$$ 70.49=\frac{7}{1+\text{i}}\cdot \left(1+\frac{1.1}{1+\text{i}}+\cdots(10 \text{ terms} )\right) $$

Step 3: Recognize the remaining factor.

We can rewrite the above equation as:

$$ 70.49=7\left(\frac{1}{1+\text{i}}+\frac{1.1}{\left(1+\text{i}\right)^2}+\cdots(10 \text{ terms })\right) $$

Now multiply the right-hand side of the above equation by \(\frac{1.1}{1.1} (=1)\).

$$ 70.49=\frac{7}{1.1}\cdot \left(\frac{1.1}{1+\text{i}}+\frac{{1.1}^2}{\left(1+\text{i}\right)^2}+\cdots(10 \text{ terms})\right) $$

Note \( (\frac{1.1}{(1+i)}+ \frac{1.1^2}{(1+i)^2} +⋯(10 \text{ terms }))≥10 \) since we must multiply it with \( \frac{7}{1.1} (=6.36) \) to get 70.49 (in fact, it is 11.08). In other words, \( {\ddot{\text{a}}}_{\overline{10|}\text{j}}10 \) with \( \text{j}=\frac{(1+\text{i})}{1.1}-1\). Therefore,

$$ 70.49=\frac{7}{1.1}\cdot {\ddot{\text{s}}}_{\overline{10|}\text{j}} $$

Using a financial calculator, we get:

$$ \begin{align*} \text{j}&=0.01851 \\ \Rightarrow0.01851&=\frac{1.1}{1+\text{i}}-1 \end{align*} $$

Solving for i we get:

$$ \text{i}=0.08 $$

Geometric Perpetuities

Recall that the present value of geometric annuities is given by

$$ \text{PV}=\frac{1- \left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\text{i}-\text{r}} $$

If we find the limit as \( \text{n}\rightarrow\infty \) of the above equation, that is,

$$ \underset { \text{n}\rightarrow\infty }{ lim } {\frac{1-\left(\frac{1+\text{r}}{1+\text{i}}\right)^\text{n}}{\text{i}-\text{r}}=}\frac{1}{\text{i}-\text{r}} $$

So that the present value of geometric progression annuities with common ratio r will be:

$$ \text{PV}=\frac{1}{\text{i}-\text{r}} $$

Alternatively, note that a geometric perpetuity is perpetuity in which the payments form a geometric progression. We can value a geometric perpetuity using two steps:

Step 1: Value each payment at the valuation date

Step 2: Value the resulting geometric series using:

$$ \text{Value of Geometric Annuity } =\frac{\text{first term}}{1-\text{ratio}} $$

Example: Geometric Perpetuity

A perpetuity immediate with annual payments has an initial payment of 12. Each subsequent payment is k% more than its preceding payment. The present value of the perpetuity is 600, using a 5% annual effective interest rate.

Determine the present value of the perpetuity using a 7% annual effective interest rate.

Solution

We start by drawing the timeline:

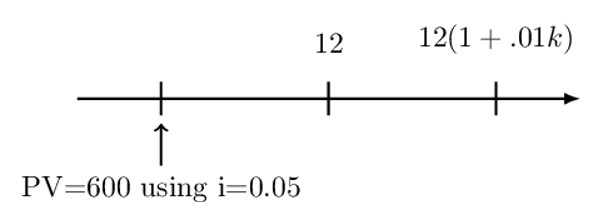
Now, we follow the two-step process:

Step 1: Value each payment at the valuation date

$$ \text{PV}=\frac{12}{1.05}+\frac{12(1+.01\text{k})}{{(1.05)}^2}+\cdots $$

Note that the payments are a sum of infinite perpetuity with the common ratio:

$$ \text{r}=\frac{1+.01\text{k}}{1.05} $$

Step 2: Value the resulting geometric series using:

$$ \begin{align*} \text{Value of Geometric Series } &=\frac{\text{first term}}{1-\text{ratio}} \\ 600&=\frac{\frac{12}{1.05}}{1-\frac{1+.01\text{k}}{1.05}}=\frac{\frac{12}{1.05}}{\frac{1.05}{1.05}-\frac{1+.01\text{k}}{1.05}}=\frac{\frac{12}{1.05}}{\frac{.05-.01\text{k}}{1.05}} \\ \Rightarrow\text{k} & =3 \end{align*} $$

Now, we can value the present value of the annuity at i=7% (intuitively using the three-step process).

$$ \text{PV}=\frac{12}{1.07}+\frac{12(1.03)}{{(1.07)}^2}+\cdots $$

The common ratio is:

$$ \text{r}=\frac{1.03}{1.07} $$

So that the present value of the annuity is:

$$ \begin{align*} \text{PV}&=\frac{\text{First Term}}{1-\text{ratio}} \\ &=\frac{\frac{12}{1.07}}{1-\frac{1.03}{1.07}}=\frac{\frac{12}{1.07}}{1-\frac{1.03}{1.07}}=300 \end{align*} $$

Alternatively, we could have used the result:

$$ \text{PV}=\frac{1}{\text{i}-\text{r}} $$

So that:

$$ \begin{align*} 600&=12\left(\frac{1}{0.05-\text{r}}\right) \\ \Rightarrow \text{r}&=\text{k}=0.03=3\% \end{align*} $$

And thus the present value of the annuity at a 7% annual rate is:

$$ \text{PV}_{0.07}=12(\frac{1}{0.07-0.03})=300 $$

Arithmetically Increasing Annuities

An arithmetic annuity is an annuity in which the payments form an arithmetic progression. A “basic” arithmetic annuity has a common difference equal to 1.

Increasing Annuity-Due

Basic increasing annuity due is denoted by \( (({\text{I}\ddot{\text{a}})}_{\overline{\text{n}}|} \). It represents the present value of increasing annuity due, which is paid at the beginning of each n-times. The timeline of the basic increasing annuity due is given below:

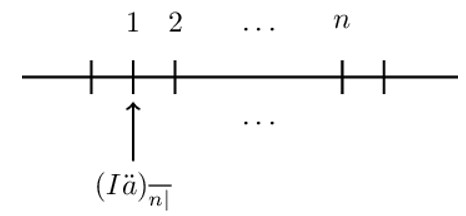
Mathematically it is defined as:

$$ {(\text{I}\ddot{\text{a}})}_{\overline{\text{n}}|}=1+2\text{v}+3\text{v}^2+\dots+\text{nv}^{\text{n}-1}\dots\dots(Eq\ 1) $$

Now multiply both sides of Eq 1 by \( \text{v}=(1+\text{i})^{-1} \) so that:

$$ \text{v}.{(\text{I}\ddot{\text{a}})}_{\overline{\text{n}}|}=\text{v}+2\text{v}^2+3\text{v}^3+\dots+\text{nv}^\text{n}\dots\dots(Eq\ 2) $$

Now subtracting Eq 2 from Eq 1 to get:

$$ {(\text{I}\ddot{\text{a}})}_{\overline{\text{n}}|}-\text{v}.\left(\text{I}\ddot{\text{a}}\right)_{\overline{\text{n}}|}=1+\text{v}+\text{v}^2+\ \ \ \ \cdots\ \ \ \ +\text{v}^{\text{n}-1}\ \ \ -\text{nv}^\text{n} \\ {\Rightarrow\left(\text{I}\ddot{\text{a}}\right)}_{\overline{\text{n}}|}\left(1-\text{v}\right)=1+\text{v}+\text{v}^2+\ \ \ \ \ \ \ \cdots\ \ +\ \text{v}^{\text{n}-1}\ \ \ -\text{nv}^\text{n} $$

Now since \( \text{d}=1-\text{v} \) and \( {\ddot{a}}_{\overline{\text{n}|}}=1+\text{v}+\text{v}^2+ \ \ \ \ \cdots\ \ \ \ +\text{v}^{\text{n}-1} \) the above equation reduces to:

$$ \begin{align*} {\text{d}.\left(\text{I}\ddot{\text{a}}\right)}_{\overline{\text{n}}|}&=({\ddot{\text{a}}}_{\overline{\text{n}|}})\ \ -\text{nv}^\text{n} \\ {\Rightarrow}\left(\text{I}\ddot{\text{a}}\right)_{\overline{\text{n}}|}&=\frac{{\ddot{\text{a}}}_{\overline{\text{n}|}}\ -\text{nv}^\text{n}}{\text{d}} \end{align*} $$

The formula above is the closed rule formula for the arithmetically increasing annuity due.

Accumulation of an Increasing Annuity Due

The following timeline illustrates the accumulation of the arithmetically increasing annuity due:

Mathematically, a basic increasing annuity due is represented as:

$$ (\text{I}{\ddot{\text{s}})}_{\overline{\text{n}|}}{=(1+\text{i})}^\text{n}+2{(1+\text{i})}^{\text{n}-1}\cdots+\text{n}(1+\text{i}) $$

Which can be proven to be:

$$ (\text{I}{\ddot{\text{s}})}_{\overline{\text{n}|}}=\frac{{\ddot{\text{s}}}_{\overline{\text{n}|}}\ -\text{n}}{\text{d}} $$

Example: Arithmetically Increasing Annuity

An annuity due with annual payments has an initial payment of 3. Each subsequent payment is 3 more than its preceding payment until reaching a final payment of 45.

Determine the present value of the annuity using a 6% annual effective interest rate.

Solution

The timeline corresponding to the question is as shown below:

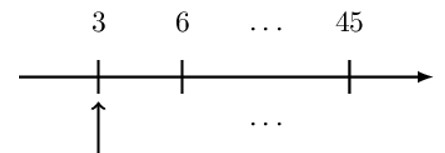
Note that the payments form an increasing annuity due with a common difference of 3 and the first payment of 3. Also, the last payment is 45 (=3×15), so that that we have 15 payments. Therefore, the present value of the annuity is given by:

$$ \text{PV}=3(\text{I}{\ddot{\text{a}})}_{\overline{15|}}=3\left[\frac{{\ddot{\text{a}}}_{\overline{15|}}-{15\text{v}}^{15}}{\text{d}}\right] $$

However, \(\text{d}=\frac{1}{1+\text{i}}\) so that:

$$ \begin{align*} \text{PV}&=3\left[\frac{{\ddot{\text{a}}}_{\overline{15|}}-{15\text{v}}^{15}}{\text{d}}\right]=3\left[\frac{{\ddot{\text{a}}}_{\overline{15|}}-{15\text{v}}^{15}}{\text{i}}\right](1+\text{i}\ ) \\ &=3\left[\frac{4.0360}{0.06}\right]\left(1.06\right) \\ \therefore \text{PV} & =213.91 \end{align*} $$

Increasing Annuity Immediate

The present value of a basic increasing annuity immediate is denoted by \(({\text{Ia})}_{\overline{\text{n}}|}\). The timeline of the increasing annuity immediate is as given below:

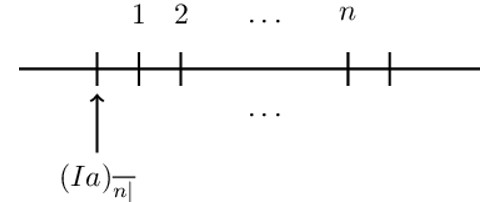
Mathematically it is defined as:

$$ \begin{align*} ({\text{Ia})}_{\overline{\text{n}}|}&=\text{v}+2\text{v}^2+3\text{v}^3+\dots+\text{nv}^\text{n} \\ &=\text{v}(1+2\text{v}+3\text{v}^2+\cdots+\text{nv}^{\text{n}-1}) \\ &=\text{v}({(\text{I}\ddot{\text{a}})}_{\overline{\text{n}|}}) \\ &=\frac{{\ddot{\text{a}}}_{\overline{\text{n}|}}\ -\text{nv}^\text{n}}{\text{d}}\cdot \text{v} \\ &=\frac{({\ddot{\text{a}}}_{\overline{\text{n}|}}\ -\text{nv}^\text{n})}{\text{iv}}\cdot \text{v} \\ &=\frac{{\ddot{\text{a}}}_{\overline{\text{n}|}}\ -\text{nv}^\text{n}}{\text{i}} \end{align*} $$

Therefore,

$$ ({\text{Ia})}_{\overline{\text{n}}|}=\frac{{\ddot{\text{a}}}_{\overline{\text{n}}|}-\text{nv}^\text{n}}{\text{i}} $$

For instance, consider an annuity-immediate with an initial payment of I (say) with increments D. therefore, the payments will be in the form \(\text{I}+\text{D},\text{I}+2\text{D} \), …. The present value of an increasing annuity immediate can be shown to be:

$$ ({\text{Ia})}_{\overline{\text{n}}|}=\left(\text{I}-\text{D}\right)\text{a}_{\overline{\text{n}}|}+\text{D}\left(\frac{{\ddot{\text{a}}}_{\overline{\text{n}}|}-\text{nv}^\text{n}}{\text{i}}\right) $$

Accumulation of an Increasing Annuity Due

The following timeline illustrates the accumulation of an annuity due:

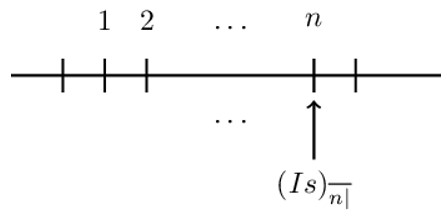
Accumulation of the arithmetically increasing annuity due is mathematically shown to be:

$$ (\text{I}{\text{s})}_{\overline{\text{n}|}}={(1+\text{i})}^{\text{n}-1}+2{(1+\text{i})}^{\text{n}-2}\cdots+\text{n} $$

And it can be proven to be:

$$ (\text{I}{\text{s})}_{\overline{\text{n}|}}=\frac{{\ddot{\text{s}}}_{\overline{\text{n}|}}\ -\text{n}}{\text{i}} $$

A summary of the relationship between arithmetically increasing annuity closed rule formula is summarized below:

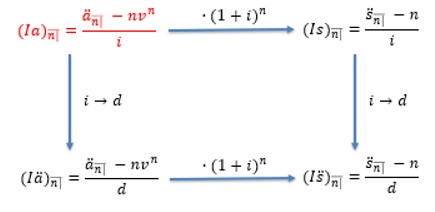
For example, the figure above implies that if we wish to move from \( \left(\text{Ia}\right)_{\overline{\text{n}|}} \text{ to } \left(\text{I}\ddot{\text{a}}\right)_{\overline{\text{n}|}} \) we change i to d respectively. Similarly, if we wish to move from \( \left(\text{Ia}\right)_{\overline{\text{n}|}}\) to \( \left(\text{Is}\right)_{\overline{\text{n}|}} \), then we accumulate the former by \( \left(1+\text{i}\right)^\text{n} \).

Arithmetically Increasing Perpetuities

In general in an increasing perpetuity, there is a first payment P and thereafter payments increase by Q (common difference) forever. The timeline is as shown below:

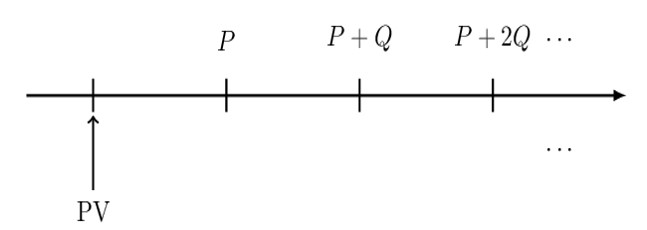
In order to derive the formula for arithmetically increasing annuity, we rearrange the increasing perpetuity as follows:

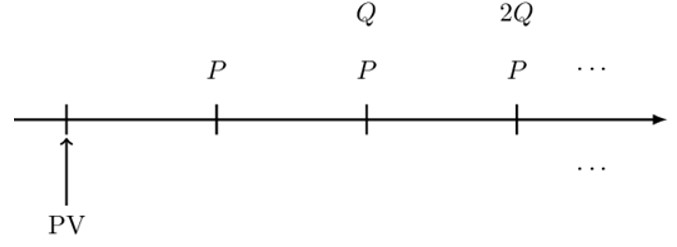
Therefore, considering the valuation date shown, we can value the arithmetic perpetuity as:

$$ \text{PV}=\text{Pa}_{\overline{\infty|}}+\text{Q}(\text{I}{\text{a})}_{\overline{\infty|}}\cdot \text{v} $$

But we know that:

$$ \text{a}_{\overline{\infty|}}=\frac{1-\text{v}^\infty}{\text{i}}=\frac{1}{\text{i}} $$

And

$$ \begin{align*} (\text{I}{\text{a})}_{\overline{\infty|}}\cdot \text{v}&=\frac{{\ddot{\text{a}}}_{\overline{\infty|}}-\infty\cdot \text{v}^\infty}{\text{i}}\cdot \text{v}=\frac{\frac{1}{\text{d}}-\infty\cdot \text{v}^\infty}{\text{i}}\cdot \text{v} \\ &=\frac{\frac{1}{\text{d}}}{\text{i}}\cdot \text{v}=\frac{\frac{1}{\text{iv}}}{\text{i}}\cdot \text{v}=\frac{1}{\text{i}^2} \\ \Rightarrow \text{PV} & =\frac{\text{P}}{\text{i}}+\frac{\text{Q}}{\text{i}^2} \end{align*} $$

Example: Arithmetically Increasing Perpetuity

Sherry has 100,000 with which to fund a scholarship to the Naval Academy. The first scholarship payment, to be made one year from now, is 3000. Subsequent annual scholarship payments are to increase by 100 each year into perpetuity.

Determine the minimum annual effective interest rate at which the money is invested, such that there will be sufficient funds to pay the scholarship payments.

Solution

The corresponding timeline for the questions is:

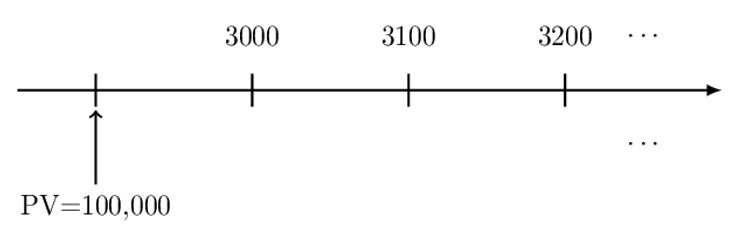
Recall that the present value (PV) of arithmetic perpetuity is given by:

$$ \text{PV}=\frac{\text{P}}{\text{i}}+\frac{\text{Q}}{\text{i}^2} $$

In this case, P=3000 and Q=100 so that:

$$ 100,000=\frac{3000}{\text{i}}+\frac{100}{\text{i}^2} $$

Forming a quadratic equation, we have:

$$ 100000\text{i}^2=3000\text{i}+100 $$

And using quadratic formula with a=100,000, b=-3000 and c=-100, we have that:

$$ \begin{align*} \text{i}&=\frac{3000\pm\sqrt{{3000}^2+4\times100,000\times100}}{2\times100,000} \\ \text{i}&=0.05,-0.02 \\ \Rightarrow\text{i}&=0.05 \end{align*} $$

Arithmetically Decreasing Annuities

Decreasing Annuity Immediate

For a decreasing annuity immediate, the timeline is as shown below:

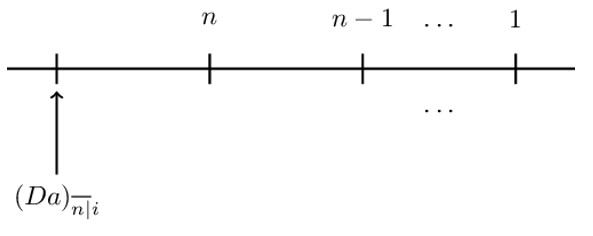
Mathematically, an arithmetically decreasing annuity immediate can be defined to be:

$$ \text{D}{\text{a}}_{\overline{\text{n}|}}=\text{nv}+(\text{n}-1)\text{v}^2+\cdots+\text{v}^\text{n} $$

It can be shown that:

$$ ({\text{Da})}_{\overline{\text{n}}|}=\frac{\text{n}-\text{a}_{\overline{\text{n}}|}}{\text{i}} $$

And the accumulation of arithmetically decreasing annuity immediate is defined as (consider the timeline below):

$$ {(\text{Ds})}_{\overline{\text{n}}|}=1+2\left(1+\text{i}\right)+\cdots+{\text{n}(1+\text{i})}^{\text{n}-1}=\frac{\text{n}\left(1+\text{i}\right)^\text{n}-\text{a}_{\overline{\text{n}}|}}{\text{i}} $$

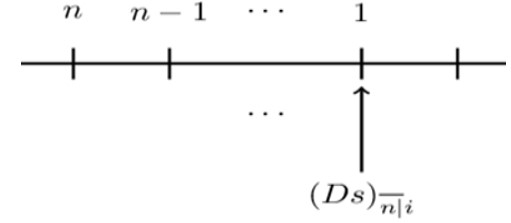
$$ \therefore{(\text{Ds})}_{\overline{\text{n}}|}=\frac{\text{n}\left(1+\text{i}\right)^\text{n}-\text{a}_{\overline{\text{n}}|}}{\text{i}} $$

Decreasing Annuity Due

For arithmetically decreasing annuity due, the timeline is as shown below:

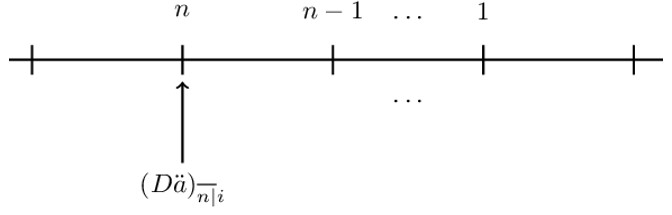
Algebraically, it can be shown that:

$$ (\text{D}{\ddot{\text{a}})}_{\overline{\text{n}|}}=\text{n}+\left(\text{n}-1\right)\text{v}+\cdots+\text{v}^{\text{n}-1}=\frac{\text{n}-\text{a}_{\overline{\text{n}|}}\ }{\text{d}} $$

For the accumulation of the basic decreasing annuity due, the timeline is as shown below:

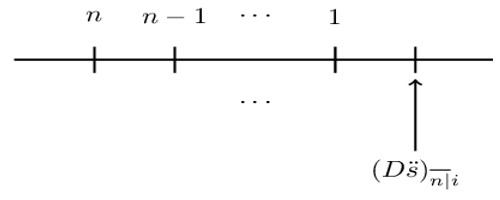
It can be shown that:

$$ (\text{D}{\ddot{\text{s}})}_{\overline{\text{n}|}}=(1+\text{i})+2\left(1+\text{i}\right)^2+\cdots+{\text{n}\left(1+\text{i}\right)}^\text{n}=\frac{\text{n}{(1+\text{i})}^\text{n}-\text{s}_{\overline{\text{n}|}}\ }{\text{d}} $$

Example: Arithmetically Decreasing Annuity Due

An annuity due with annual payments has an initial payment of 75. Each subsequent payment is 4 less than its preceding payment until reaching a final payment of 27.

Determine the accumulated value of the annuity using a 9% annual effective interest rate.

Solution

Given the information in the question, the timeline corresponding to the question is:

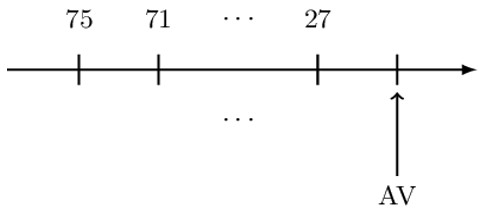
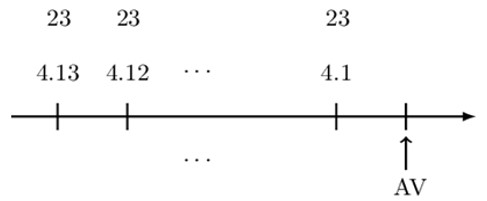
Note that the payments represent an arithmetically increasing annuity due with a common difference of (-)4. At this point, we cannot use the valuation symbols, and thus we need to modify our payments. Note that the last payment can be modified as:

$$ 27=4\ast1+23 $$

Similarly to the first and the second payments, we have that:

$$ 75=4\cdot 13+23 \left(\text{ Hence we have 13 payments } \right) $$

And

$$ 71=4\ast12+23 $$

The timeline is therefore modified to:

So the accumulated value of the annuity is:

$$ \begin{align*} \text{AV}&=23{\ddot{\text{s}}}_{\overline{13|}}+4(\text{D}{\ddot{\text{s}})}_{\overline{13|}} \\ &=23{\ddot{\text{s}}}_{\overline{13|}}+4\left[\frac{13\left(1+\text{i}\right)^{13}-\text{s}_{\overline{13|}}}{\text{d}}\right] \\ &=23{\ddot{\text{s}}}_{\overline{13|}}+4\frac{13\left(1+\text{i}\right)^{13}-\text{s}_{\overline{13|}}}{\text{i}}(1+\text{i})\\ \therefore \text{AV} & =1,394.25 \end{align*} $$

Alternatively, we could arrange the payments as follows:

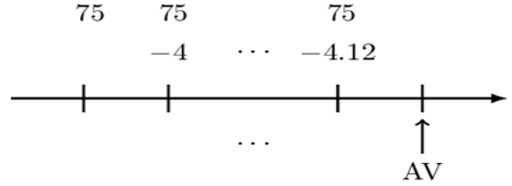
So that the accumulation of the annuity is given by:

$$ \begin{align*} \text{AV}&=75{\ddot{\text{s}}}_{\overline{13|}}-4(\text{I}{\ddot{\text{s}})}_{\overline{12|}}=75{\ddot{\text{s}}}_{\overline{13|}}-4\frac{{\ddot{\text{s}}}_{\overline{12|}}-12}{\text{d}} \\ &=75{\ddot{\text{s}}}_{\overline{13|}}-4\frac{{\ddot{\text{s}}}_{\overline{12|}}-12}{\text{i}}(1+\text{i}) \\ &=75{\ddot{\text{s}}}_{\overline{13|}}-4\frac{{\ddot{\text{s}}}_{\overline{12|}}-12}{0.09}\left(1+0.09\right) \\ &=1,394.25 \end{align*} $$

The relationship between the decreasing annuities is shown in the diagram below:

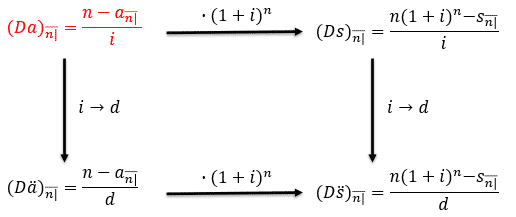
The interpretation is similar to that of arithmetically increasing annuities.

Increasing Annuity Paid Continuously

It is very important to distinguish between two cases of annuities of this type:

1. An annuity that is continuous and increases at the rate r per unit time throughout the rth time period denoted by \( {(\text{I}\overline{\text{a}})}_{\overline{\text{n}}|} \).

It is defined to be:

$$ {(\text{I}\overline{\text{a}})}_{\overline{\text{n}}|}=\sum_{\text{r}=1}^{\text{n}}\left(\int_{\text{r}-1}^{\text{r}}{\text{rv}^\text{t}}\text{dt}\right) $$

Which can be shown to be:

$$ {(\text{I}\overline{\text{a}})}_{\overline{\text{n}}|}=\frac{{\ddot{\text{a}}}_{\overline{\text{n}}|}-\text{nv}^\text{n}}{\delta} $$

An annuity that is continuous and increases at the rate t at time t denoted by \({(\overline{\textbf{Ia}})}_{\overline{\textbf{n}}|}\).

It is defined as :

$$ {(\overline{\text{Ia}})}_{\overline{\text{n}}|}.=\int_{0}^{\text{n}}{\text{tv}^\text{t}\text{dt}} $$

And it can be proved to be:

$$ {(\overline{\text{Ia}})}_{\overline{\text{n}}|}=\frac{{\overline{\text{a}}}_{\overline{\text{n}}|}-\text{nv}^\text{n}}{\delta} $$

(NOTE: distinguish the position of the bars.)

Example: Increasing Annuity Paid Continuously

A tenant pays the rent continuously for 5 years. He pays 3000 dollars for the first year, and thereafter the rent increases by 500 dollars per year.

Find the present value of the rent at the start of 5 years, assuming the effective rate of interest to be 6%.

Solution

Clearly, the present value will be:

$$ \begin{align*} &=2500{\overline{\text{a}}}_{\overline{5}|}+500{(\text{I}\overline{\text{a}})}_{\overline{5}|} \\ &=2500\left[\frac{1-1.06^{-5}}{\text{ln} \left(1.06\right)}\right]+500\left[\frac{{\ddot{\text{a}}}_{\overline{5}|}-5\text{v}^5}{\text{ln}\left(1.06\right)}\right] \\ &=2500\times4.375+500\times12.5078 \\ &=17191.40 \text{ dollars}. \end{align*} $$

2.5. Rainbow Annuity

A basic rainbow annuity is an annuity in which the payments are:

$$ 1, 2,\cdots,\left(\text{n}-1\right), \text{n} , \left(\text{n}-1\right), \cdots, 2, 1 $$

A basic rainbow annuity increases up to the peak n, and it starts to decrease. The timeline of the rainbow annuity is shown below:

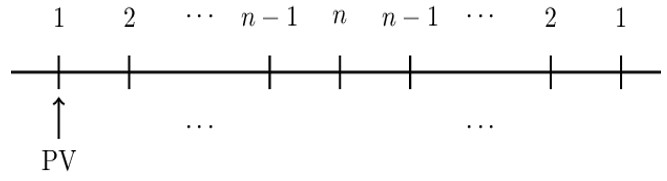
The present value of the basic rainbow annuity due is given by:

$$ \text{PV}=\left({\ddot{\text{a}}}_{\overline{\text{n}|}}\right)^2 $$

This is a very important equation worth to remember. However, we can value rainbow annuity by grouping the payments as follows:

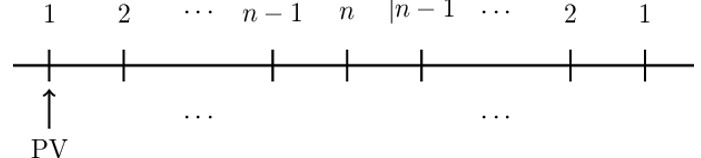
So that the present value of the basic rainbow annuity is given by:

$$ \text{PV}=(\text{I}{\ddot{\text{a}})}_{\overline{\text{n}|}}+(\text{D}{\ddot{\text{a}})}_{\overline{\text{n}-1|}}\cdot \text{v}^\text{n} $$

However, this is a correct way of valuing rainbow annuity, but it is important to remember the basic formula, \( \text{PV}=\left({\ddot{\text{a}}}_{\overline{\text{n}|}}\right)^2\) since it is applicable to many questions.

Example: Rainbow Annuity

Using i=0.06, determine the present value at the valuation date shown by the arrow.

Solution

To value the rainbow annuity, we need to choose an intermediate valuation date \({\text{PV}}_{1}\) as shown on the timeline below:

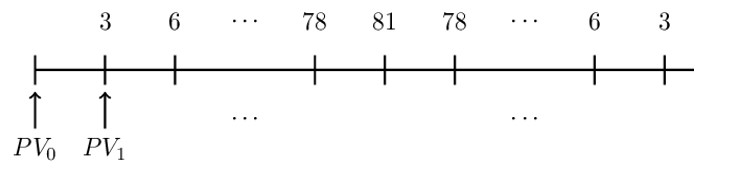So that,

$$ {\text{PV}}_0={\text{PV}}_1\cdot \text{v}_{0.06} $$

But

$$ \begin{align*} {\text{PV}}_1&=3\cdot \left({\ddot{\text{a}}}_{\overline{\text{n}|}}\right)^2 \\ \Rightarrow{\text{PV}}_0&=\left[3\cdot \left({\ddot{\text{a}}}_{\overline{\text{n}|}}\right)^2\right]\cdot \text{v}_{0.06} \end{align*} $$

However, we need to find the value n. Recall that n is the peak of the rainbow annuity. In this case, the peak is 81 (=3×27), so that n=27. Therefore,

$$ {\text{PV}}_0=\left[3\cdot \left({\ddot{\text{a}}}_{\overline{27|}}\right)^2\right]\cdot \text{v}_{0.06}=\frac{3\cdot \left({\ddot{\text{a}}}_{\overline{27|}}\right)^2}{1.06}=554.97 $$

Example: Rainbow Annuity (Tricky)

An annuity immediate with annual payments has the first payment of 1. Subsequent payments increase by 1 until reaching a payment of 12. The next payment is also 12, and then payments decrease by 1 until reaching a payment of 1.

Determine an expression for the present value of this annuity.

Solution

The first step is to draw a timeline:

A natural approach to this problem is to group the payments into two groups: one group up to the first payment of 12 and the second group from the second payment of 12 as shown below:

So that the present value of the annuity is:

$$ \text{PV}=(\text{I}{\text{a})}_{\overline{12|}}+(\text{D}{\text{a})}_{\overline{12|}}\cdot \text{v}^{12} $$

However, if we were asked to calculate the value of i (periodic effective interest rate), it will be very complex using the equation above.

An easy way is to rearrange the payments is as follows:

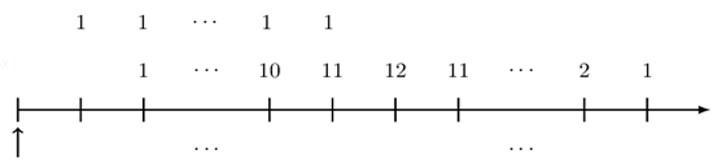
Note that the arrangement is such that, we subtract 1 (and move up) from each payment up to the first payment of 12. The payments of 1 is a basic annuity immediate, and the remaining payments are a basic rainbow annuity. From the rearrangement, the present value of the annuity is:

$$ \begin{align*} \text{PV}&=\text{a}_{\overline{12|}}+{({\ddot{\text{a}}}_{\overline{12|}})}^2\cdot \text{v}^2 \\ &{=\text{a}}_{\overline{12|}}+{({\ddot{\text{a}}}_{\overline{12|}}\cdot \text{v})}^2 \\ \Rightarrow \text{PV}&=\text{a}_{\overline{12|}}+{(\text{a}_{\overline{12|}})}^2 \end{align*} $$

Therefore, we can calculate the value of i easily from this equation. For example, let

PV=82.9. Then,

$$ 82.9=\text{a}_{\overline{12|}}+{(\text{a}_{\overline{12|}})}^2 $$

Note that the resulting equation is a quadratic equation which when solved,

$$ \text{a}_{\overline{12|}}=8.61866 $$

Using a financial calculator, you should find:

$$ \text{i}=0.055 $$

Term of an Annuity

All along, we have been assuming that the term of the annuity n is an integer. We now consider a case where n may not be an integer. For instance, consider an annuity-immediate \( \text{a}_{\overline{\text{n+t}}|} \) where t is such that 0<t<1.

We know that:

$$ {\text{a}}_{\overline{\text{n+t}}|}=\frac{1-\text{v}^{\text{n+t}}}{\text{i}} $$

This can be simplified as:

$$ \begin{align*} {\text{a} }_{\overline{\text{n+t}}|}&=\frac{1-\text{v}^{\text{n+t}}}{\text{i}} \\ &=\frac{\left(1-\text{v}^\text{n}\right)+(\text{v}^\text{n}-\text{v}^{\text{n+t}})}{\text{i}} \\ &=\frac{\left(1-\text{v}^\text{n}\right)}{\text{i}}+\frac{\text{v}^\text{n}-\text{v}^{\text{n}+\text{t}}}{\text{i}} \\ &{=\text{a}}_{\overline{\text{n}}|}+\text{v}^{\text{n+t}}\left(\frac{\left(1+\text{i}\right)^\text{t}-1}{\text{i}}\right){=\text{a}}_{\overline{\text{n}}|}+\text{v}^{\text{n+t}}\text{s}_{\overline{\text{t}}|} \end{align*} $$

So,

$$ {\text{a}}_{\overline{\text{n+t}}|}={\text{a}}_{\overline{\text{n}}|}+\text{v}^{\text{n+t}}\text{s}_{\overline{\text{t}}|} $$

which can be evaluated easily.

Example: Term of an Annuity

Evaluate \( {\text{a}}_{\overline{3.25}|}@10\%\) per annum.

Solution

Clearly,

\(\text{t}=0.25 \text{ and } \text{n}=3\)

$$ \begin{align*} {\Longrightarrow}{\text{a}}_{\overline{\textbf{3}.\textbf{25}}|} &={\textbf{a}}_{\overline{\textbf{3}}|}+\textbf{v}^{\textbf{3}.\textbf{25}}({\textbf{s}}_{\overline{\textbf{0}.\textbf{25}}|}) \\ &=\frac{1-1.10^{-3}}{0.10}+1.10^{-3.25}\left(\frac{1.10^{0.25}-1}{0.10}\right)\\&=2.66375 \end{align*} $$

Similar simplifications are applied to annuity-due.

Other Non-level Annuities

There are those annuities which are not of an equal amount. To find the present value of discrete cash flow, we use the first principle method. That is:

$$ \text{PV}=\sum_{\text{i}}^{\text{N}}{\text{x}_\text{i}\text{v}^{\text{t}_\text{i}}} $$

where \(\text{x}_\text{i}\) is the annual payment. If there is a mixture of both continuous and discrete cash flows, then we can use the following formula:

$$ \text{PV}=\sum_{\text{i}}^{\text{N}}{\text{x}_\text{i}\text{v}^{\text{t}_\text{i}}}+\int_{-\infty}^{\infty}{\rho\left(\text{t}\right)\text{v}^\text{t}} $$

Where \(\rho (t)\) is the amount of payment per unit time t.