Interest Rate Swaps

AnalystPrep’s Actuarial Exams Preparation Materials

For our question bank, study notes, quizzes, and all our video lessons: https://analystprep.com/shop/learn-practice-package-for-soa-exam-fm/

After completing this chapter, you should be able to:

1. Define and recognize the definitions of the following terms: swap rate, swap term or swap tenor, notional amount, market value of a swap, settlement dates, settlement period, counterparties, deferred swap, amortizing swap, accreting swap, interest rate swap net payments.
2. Given sufficient information, calculate the market value, notional amount, spot rates or swap rate of an interest rate swap, deferred or otherwise, with either constant or varying notional amount.

General Swaps

A swap is an agreement between two counterparties to exchange cash flows in the future. The counterparties are the two parties that participate in the swap transaction. The terms most used in swap contracts are as follow:

• Swap Term (or Swap Tenor): An interest rate swap tenor is the period of the swap contract. The swap term can be short, such a few months or longer, as ten years.
• Settlement Date: The settlement date is the agreed date that the counterparties will exchange the cash flows (interest rate payments).
• Settlement Period: The settlement period is the length of time between two settlement dates. The settlement periods depend on the agreement of the counterparties. The settlement can be monthly, quarterly, or even shorter periods agreed by the counterparties.
• Swap Rate: Mostly defined in the interest rate swaps, the swap rate is a fixed interest rate given in an interest swap contract. The swap rate is a fixed interest rate, i, that one counterparty demands in exchange for the uncertainty of having to pay the variable rate (floating interest rate) over time.
• Floating Interest Rate: Also defined in interest rate swaps, the floating interest rate is the basis for computing floating interest payments at each settlement date. Examples of the floating interest rates include LIBOR (London Interbank Offer Rate) and the Treasury Bill Rate. The floating rate is stated with a predetermined spread to the reference rate, such as 1-year LIBOR plus 30 basis points.

General Set-up of a Swap

By the definition of a swap, one set of payments (level) is “swapped” for another set of payments (non-level, or floating). Consider the following three-period timeline:

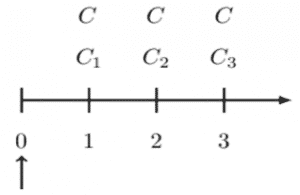
On the timeline above, the level payment \(C\) at each period is swapped with non-level payments,\(C_k\) where \((k=1,2,3)\). The swap transactions are done in a “fair way.” That is, the present value at time 0 of interest rate payments are equal to each other. Note that swaps are in the context of the term structure of interest rates. Using the timeline above, it implies that:

$$ C_1\cdot\ v_1+C_2\cdot\ v_2^2+C_3\cdot\ v_3^3=C\cdot\ v_1+C\cdot\ v_2^2+C\cdot\ v_3^3 $$

In the equation above, the level payments are usually known. On the other hand, non-level payments are unknown. If we make \(C\) the subject of the formula, we have:

$$ C=\frac{C_1\cdot v_1+C_2\cdot v_2^2+C_3\cdot v_3^3}{v_1+v_2^2+v_3^3} $$

The value given by the equation above is called the swap price.

In a swap contract, there are two counterparties: the payer and the receiver. The payer pays the fixed swap price and receives the non-level payments while the receiver receives the fixed swap price and pays the non-level payments.

The net swap payment (NSP) is the amount received minus the amount paid. As such, for the payer, the net swap payment at time \(k\) is given by:

$$ NSP_K=C_k-C $$

On the other hand, the net swap payment for the receiver at time k is given by:

$$ NSP_K=C-C_k $$

As an example, assume that in the timeline above, the payments are as follows:

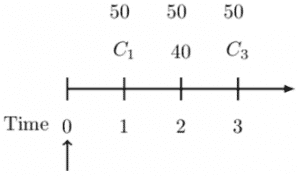
Therefore, the net swap payment for the payer at time 2 is:

$$ NSP_2=C_2-C=40-50=-10 $$

That is, the payer owes 10 at time 2. Intuitively, the net swap payment for the receiver is

$$ NSP_2=C-C_2=50-40=10 $$

Interest Rate Swaps

An interest rate swap is a scheme where you exchange a payment stream at a predetermined fixed rate of interest for a payment stream at a variable (or floating) rate. In other words, interest payments are only exchanged. Consider that following illustration:

Illustration: Interest Rate Swap

The diagram above is an interest rate swap between two counterparties A and B. Counterparty A pays a fixed rate of 4.5% to B, whereas B pays a variable rate linked to LIBOR of LIBOR + 100 bps.

The counterparties in the transaction are parties A and B, and the swap rate is the fixed rate in the interest rate swap, in this case, 4.5%.

Mathematics of Interest Rate Swaps

Consider the following timeline:

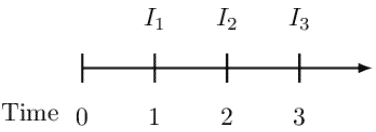
Note that the interest rate amounts are based on the notional amount. The notional amount at time \(k\), denoted by \(N_k\), is the amount of money on which interest amounts are calculated for the following period.

As a matter of emphasis, swaps are transacted in the context of the term structure of interest rates. As such, using the timeline above, from time 0 to time 1, we use a one-year spot rate \(s_1\) (equivalent to one-year forward rate from time 0 to time 1) so that the interest amount at time 1 is:

$$ I_1=N_0\cdot\ s_1 $$

From time 1 to time 2, we use a one-year forward rate from time 1 to time 2, \(f_{[1,2]}\) so that the interest payment at time two is:

$$ {I_2=N}_1\cdot {f_{[1,2]}} $$

Intuitively, from time two to time three, we use a one-year forward rate from time 2 to time 3, \(f_{[2,3]}\) so that the interest payment is:

$$ I_3=N_2\cdot {f_{[2,3]}} $$

The following timeline summarizes the above interest payments:

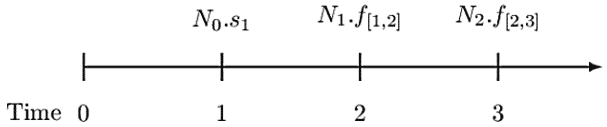
Note that an interest rate swap exchanges a non-flat yield curve for a flat yield curve. As such, notice that the payments above are based on the non-flat yield curve (variable interest amounts). Thus, the payment at time \(k\) is swapped with a payment of \(N_{k-1}.i\) where \(i\) is a fixed interest rate. Therefore, for the timeline above, the fixed interest amounts for times 1, 2, and 3 are \(N_0.i\), \(N_1.i\) and \(N_2.i\) respectively. Consider the following timeline:

The fixed interest \(i\) is called a swap rate.

In the context of the interest rate swaps, the payer pays the fixed-rate and receives the variable interest rate while the receiver receives a fixed interest rate and pays the variable interest rate. Also, recall that the net swap payment is defined as the amount received minus the amount paid. Thus, the net swap payment for the payer at time \(k\) is given by:

$$ \begin{align*} NSP_k&=N_{k-1}\cdot\ f_{\left[k-1,k\right]}-N_{k-1}\cdot i\\ &=N_{k-1}\cdot\left(f_{\left[k-1,k\right]}-i\right) \end{align*} $$

On the other hand, the net swap payment for the receiver at time \(k\) is given by:

$$ \begin{align*} NSP_k&=N_{k-1}\cdot\ i-N_{k-1}\cdot\ f_{\left[k-1,k\right]}\\ &=N_{k-1}\cdot(i-f_{\left[k-1,k\right]}) \end{align*} $$

Continuing with our timeline example, swaps are usually transacted in a fair way. That is, the present values of the payments at time 0 must be equal. In the case of our interest rate swap illustration, it implies that:

$$ N_0\cdot\ f_{\left[0,1\right]}\cdot v_1+N_1\cdot f_{\left[1,2\right]}\cdot v_2^2+N_2\cdot f_{\left[2,3\right]}\cdot v_3^3=N_0\cdot i\cdot v_1+N_1\cdot i\cdot v_2^2+N_2\cdot i\cdot v_3^3 $$

If we make \(i\) the subject of the formula, we get:

$$ i=\cfrac{N_0\cdot f_{[0,1]}\cdot v_1+N_1\cdot f_{[1,2]} \cdot v^2_2+N_2 \cdot f_{[2,3]} \cdot v^3_3}{N_0 \cdot v_1+N_1 \cdot v^2_2+N_2 \cdot v^3_3} $$

Note that the notional amount needs not be equal at each period. The notional amount can be level or varying at each period.

Level Notional Swaps

Level notional swaps are a special case swap where the notional amount is level for all periods. We shall base our discussion on the interest rate swaps, which is the main aim of the chapter. Now recall that an interest rate swap involves exchanging fixed interest payments \((N_{\left(K-1\right)}.i)\) for the variable interest payments \((N_{k-1}\cdot\ f_{\left[k-1,k\right]})\). Recall the following timeline:

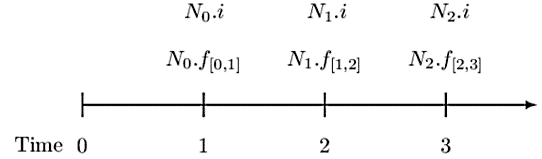
The interest rate swap is done in a fair way so that:

$$ N_0\cdot\ f_{\left[0,1\right]}\cdot v_1+N_1\cdot f_{\left[1,2\right]}\cdot v_2^2+N_2\cdot f_{\left[2,3\right]}\cdot v_3^3=N_0\cdot i\cdot v_1+N_1\cdot i\cdot v_2^2+N_2\cdot i\cdot v_3^3 $$

If we make \(i\) the subject of the formula, we get:

$$ i=\cfrac{N_0\cdot f_{[0,1]}\cdot v_1+N_1\cdot f_{[1,2]} \cdot v^2_2+N_2 \cdot f_{[2,3]} \cdot v^3_3}{N_0 \cdot v_1+N_1 \cdot v^2_2+N_2 \cdot v^3_3} $$

If the notional amount is level at each period is level at N, then the timeline changes to:

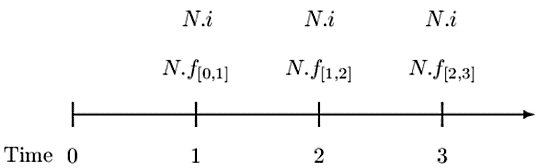
Also, the formula for the swap rate is given by:

$$ \begin{align*} i&=\frac{N\cdot f_{\left[0,1\right]}\cdot v_1+N\cdot f_{\left[1,2\right]}\cdot v_2^2+N\cdot f_{\left[2,3\right]}\cdot v_3^3}{N\cdot v_1+N\cdot v_2^2+N\cdot v_3^3}\\ \Rightarrow i&=\cfrac{f_{[0,1]}\cdot v_1+f_{[1,2]}\cdot v^2_2+f_{[2,3]} \cdot v^3_3}{v_1+v^2_2+v^3_3} \end{align*} $$

The formula above is computationally intensive. Fortunately, there is a way to simplify the formula.

Now recall the formula for calculating forward rates:

$$ \left(1+f_{\left[k,n\right]}\right)^{n-k}=\frac{\left(1+s_n\right)^n}{\left(1+s_k\right)^k} $$

Where

\(f_{\left[k,n\right]}\) = forward rate for times \(k\) to time \(n\)

\(s_n\) = \(n\)-year spot rate

\(s_k\) = \(k\)-year spot rate

Therefore,

$$ \begin{align*} \left(1+f_{\left[0,1\right]}\right)^{1-0}&=\frac{\left(1+s_1\right)^1}{\left(1+s_0\right)^0} \\{\therefore f}_{\left[0,1\right]}&=\left(1+s_1\right)^1-1 \end{align*} $$

It, therefore, implies that,

$$ f_{[0,1]}\cdot v_1=[(1+s_1)^1-1]v^1=v^0-v^1=1-v^1 $$

Similarly,

$$ f_{[1,2]}=\cfrac {(1+s_2)^2}{(1+s_1)}-1 $$

Thus,

$$ \begin{align*} \Rightarrow\ f_{\left[1,2\right]}\cdot v_2^2&=\left[\frac{\left(1+s_2\right)^2}{\left(1+s_1\right)}-1\right]\cdot v_2^2 \\ &=\frac{{v_2^2\left(1+s_2\right)}^2}{\left(1+s_1\right)}-v_2^2\\ &=\frac{1}{\left(1+s_1\right)}-v_2^2=v_1^1-v_2^2 \end{align*} $$

Also,

$$ \begin{align*} f_{\left[2,3\right]}&=\frac{\left(1+s_3\right)^3}{\left(1+s_2\right)^2}-1\\ \Rightarrow\ f_{\left[2,3\right]}\cdot v_3^3 &=\left[\frac{\left(1+s_3\right)^3}{\left(1+s_2\right)^2}-1\right]\cdot v_3^3\\ &=\left[\frac{{v_3^3\left(1+s_3\right)}^3}{\left(1+s_2\right)^2}-v_3^3\right]\\ &=\left[\frac{1}{\left(1+s_2\right)^2}-v_3^3\right]=v_2^2-v_3^3 \end{align*}$$

If we restate the formulas, we have:

$$ \begin{align*} f_{\left[0,1\right]}\cdot v_1&=v_0^0-v_1\\ f_{\left[1,2\right]}\cdot v_2^2&=v_1^1-v_2^2\\ f_{[2,3]}\cdot v^3_3&=v^2_2-v^3_3 \end{align*} $$

It is easy to see that pattern, and thus the formula for swap rate changes to:

$$ \begin{align*} i&=\frac{\left[f_{\left[0,1\right]}\cdot v_1\right]+\left[f_{\left[1,2\right]}\cdot v_2^2\right]+\left[f_{\left[2,3\right]}\cdot v_3^3\right]}{v_1+v_2^2+v_3^3}\\ &=\frac{\left[1-v_1\right]+\left[v_1-v_2^2\right]+\left[v_2^2-v_3^3\right]}{v_1+v_2^2+v_3^3}\\ \therefore i&=\frac{1-v_3^3}{v_1+v_2^2+v_3^3} \end{align*} $$

The last result is seemingly easier to calculate. To get a better grip on level notional interest rate swap, assume now that we are dealing with a four-period timeline:

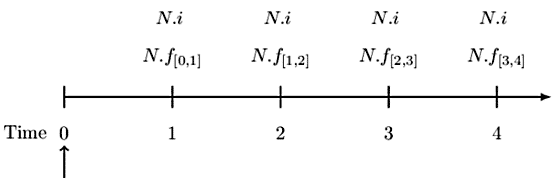
Then,

$$ \begin{align*} &N\cdot\ f_{\left[0,1\right]}\cdot v_1+N\cdot f_{\left[1,2\right]}\cdot v_2^2+N\cdot f_{\left[2,3\right]}\cdot v_3^3+N\cdot f_{\left[2,3\right]}\cdot v_3^3\\ &=N\cdot i\cdot v_1+N\cdot i\cdot v_2^2+N\cdot i\cdot v_3^3+N\cdot i\cdot v_4^4\\ \Rightarrow\ i&=\frac{\left[f_{\left[0,1\right]}\cdot v_1\right]+\left[f_{\left[1,2\right]}\cdot v_2^2\right]+\left[f_{\left[2,3\right]}\cdot v_3^3\right]+\left[f_{\left[3,4\right]}\cdot v_4^4\right]}{v_1+v_2^2+v_3^3+v_4^4}\\ &=\frac{\left[1-v_1\right]+\left[v_1-v_2^2\right]+\left[v_2^2-v_3^3\right]+\left[v_3^3-v_4^4\right]}{v_1+v_2^2+v_3^3+v_4^4}\\ \Rightarrow i&=\frac{1-v_4^4}{v_1+v_2^2+v_3^3+v_4^4} \end{align*} $$

So generally, for level notional interest swap the swap rate is given by:

$$ i=\frac{1-v_n^n}{\sum_{j=1}^{n}v_j^j}\ $$

Example: Determining Net Swap Payment for the Interest Rate Swap

Beth has a four-year variable rate loan of 1,000, where the interest rate is reset annually to the one-year spot interest rate. She pays interest only at the end of each year and repays the principal of 1000 at the end of year 4. Beth enters into a four-year interest rate swap with an annual settlement wherein she pays a fixed rate and receives the variable rate. At the time that the swap is entered into, spot rates are \(s_k=k%\) for \(k=1, 2, 3, 4\).

Determine Beth’s net swap payments for each year.

Solution

Let the swap rate be \(i\). Then from the given information in the question, we have the following spot rates: \(s_1\)=0.01, \(s_2\)=0.02, \(s_3\)=0.03 and \(s_4\)=0.04.

The appropriate timeline is given by:

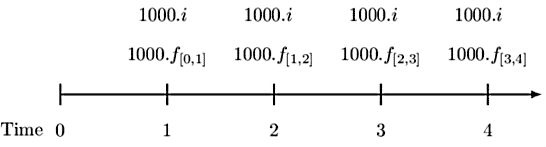
Consider time 2. Since Beth pays a fixed interest payment each year, we need:

$$ NSP_2=1000.f_{\left[1,2\right]}-1000.i=1000(f_{\left[1,2\right]}-i) $$

Thus, we need to determine the swap rate \(i\) and the one-year forward rate from time 1 to time 2. Now, since this is a four-year level notional interest rate swap, we can use the formula:

$$ \begin{align*} i&=\frac{1-v_4^4}{v_1+v_2^2+v_3^3+v_4^4}\\ &=\frac{1-\left(1.04\right)^{-4}}{\left(1.01\right)^{-1}+\left(1.02\right)^{-2}+\left(1.03\right)^{-3}+\left(1.04\right)^{-4}}\\ &=0.03901 \end{align*} $$

Now, using the formula,

$$ \left(1+f_{\left[k,n\right]}\right)^{n-k}=\frac{\left(1+s_n\right)^n}{\left(1+s_k\right)^k} $$

Where

\(f_{\left[k,n\right]}\)= forward rate for times \(k\) to time \(n\)

\(s_n\) = \(n\)-year spot rate

\(s_k\) = \(k\)-year spot rate

Then,

$$ \begin{align*} \left[1+f_{\left[1,2\right]}\right]^{2-1}&=\frac{\left(1+s_2\right)^2}{\left(1+s_1\right)}\\ \Rightarrow f_{\left[1,2\right]}&=\frac{\left(1+s_2\right)^2}{\left(1+s_1\right)}-1=\frac{\left(1.02\right)^2}{\left(1.01\right)}-1\\ &=0.03009 \end{align*} $$

Thus we need,

$$ \begin{align*} NSP_2&=1000\left(f_{\left[1,2\right]}-i\right)\\ &=1000\left(0.03009-0.03901\right)\\ &=-8.92 \end{align*} $$

Similarly, we can calculate Beth’s net swap payments in other periods. Consider the following timeline with the corresponding information:

Note that the forward rates are calculated as follows:

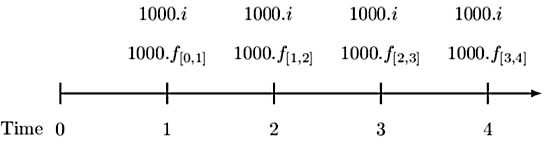
$$ \begin{align*} f_{\left[0,1\right]}&=s_1=0.01\\ f_{\left[2,3\right]}&=\frac{\left(1.03\right)^3}{\left(1.02\right)^2}-1=0.05029\\ f_{\left[3,4\right]}&=\cfrac {(1.04)^4}{(1.03)^3}-1=0.07058 \end{align*} $$

Beth’s net swap payment at time 1 is:

$$ {NSP}_1=1000\left(s_1\right)-1000\left(i\right)=10-39.01=-29.01 $$

That is, at time 1, Beth owes 29.01.

At time 3, the net swap payment is:

$$ {NSP}_3=1000\left(f_{\left[2,3\right]}\right)-1000\left(i\right)=50.29-39.01=11.28 $$

Therefore at time 3, Beth is paid 11.28.

Lastly, at time 4, the net swap payment is given by:

$$ {NSP}_4=1000\left(f_{\left[3,4\right]}\right)-1000\left(i\right)=70.58-39.01=31.57 $$

Thus, Beth is paid 31.57 at time 4.

It is crucial to note that the present value of the net swap payments is always 0. That is,

$$ \begin{align*} PV&=-29.01v_1-8.92v_2^2+11.28v_3^3+31.57v_4^4\\ &=\frac{-29.01}{1.01}+\frac{-8.92}{{1.02}^2}+\frac{11.28}{{1.03}^3}+\frac{31.57}{{1.04}^4}\\ &=0 \end{align*} $$

As such, a swap can be defined as the fixed interest rate that makes the present value of the net swap payments equal to zero.

Market Value of an Interest Rate Swap

The market value of a swap is the present value of the future net swap payments using the current term structure of interest rates. The market value of interest rate swaps is mostly calculated when a party in a swap contract transfers all rights and obligations to another party or cancels a swap with another counterparty at any time within the swap tenor.

The market value of an interest rate swap can be negative or positive. A negative swap market value implies that the outstanding swap is not competitive under the prevailing term structure of interest rate, and thus the seller must compensate the buying counterparty. Note that the seller could be a fixed-rate-payer or floating-rate-payer of the interest swap. Lastly, it important to note that the market values of the counterparties in an interest rate swap have the same absolute value (but opposite signs).

Example: Market Value of an Interest Rate Swap

Beth has a four-year variable rate loan of 1,000, where the interest rate is reset annually to the one-year spot interest rate. She pays interest only at the end of each year and repays the principal of 1000 at the end of year 4. Beth enters into a four-year interest rate swap with an annual settlement wherein she pays a fixed rate and receives the variable rate. At the time that the swap is entered into, spot rates are \(s_k\)=k% for k=1, 2, 3, 4.

One year has passed since Beth entered into the swap. The 1-year spot rate is now 4.5%. The 2-year spot rate is now 5.5%, and the 3-year spot rate is 6.5%.

Determine the current market value of Beth’s position in the swap.

Solution

The first step is to calculate the swap rate. Note that we shall be using the original information given. The timeline is given by:

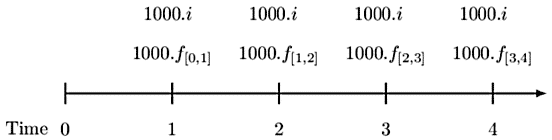
Now, since this is a four-year level notional interest rate swap, we can use the formula:

$$ \begin{align*} i&=\frac{1-v_4^4}{v_1+v_2^2+v_3^3+v_4^4}\\ &=\frac{1-\left(1.04\right)^{-4}}{\left(1.01\right)^{-1}+\left(1.02\right)^{-2}+\left(1.03\right)^{-3}+\left(1.04\right)^{-4}}\\ &=0.03901 \end{align*} $$

Now, after one year, the term structure of interest rate has changed. In other words, the spot and forward rates have changed, and the valuation date has now shifted to time 1 (our new time, 0). Thus, the new timeline is as follows:

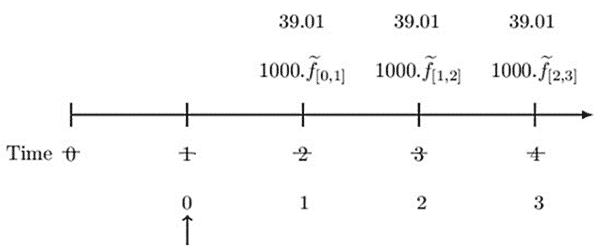
Notice the crossed-out times and the updated time. The one-, two- and three-year spot rates are 0.045, 0.055, and 0.065, respectively. That is, \({\widetilde{s}}_1=0.045,\ {\widetilde{s}}_2=0.055\) and \({\widetilde{s}}_3=0.065\).

The market value of a swap is the present value of the future net swap payments using the current term structure of interest rates. Since Beth is a payer, then, the market value is given by:

$$ \begin{align*} {MV}_1&=\left(1000\cdot{\widetilde{f}}_{\left[0,1\right]}-39.01\right){\widetilde{v}}_1+\left(1000\cdot{\widetilde{f}}_{\left[1,2\right]}-39.01\right){\widetilde{v}}_2^2\\ &+\left(1000\cdot{\widetilde{f}}_{\left[2,3\right]}-39.01\right){\widetilde{v}}_3^3\\ &=1000\left({\widetilde{f}}_{\left[0,1\right]}\cdot{\widetilde{v}}_1+{\widetilde{f}}_{\left[1,2\right]}\cdot{\widetilde{v}}_2^2+{\widetilde{f}}_{\left[2,3\right]}\cdot{\widetilde{v}}_3^3\right)-39.01\left({\widetilde{v}}_1+{\widetilde{v}}_2^2+{\widetilde{v}}_3^3\right)\\ &=1000\left(\left(1-{\widetilde{v}}_1\right)+\left({\widetilde{v}}_1-{\widetilde{v}}_2^2\right)+\left({\widetilde{v}}_2^2-{\widetilde{v}}_3^3\right)\ \right)-39.01\left({\widetilde{v}}_1+{\widetilde{v}}_2^2+{\widetilde{v}}_3^3\right)\\ &=1000\left(1-{\widetilde{v}}_3^3\ \right)-39.01\left({\widetilde{v}}_1+{\widetilde{v}}_2^2+{\widetilde{v}}_3^3\right)\\ &=67.48 \end{align*} $$

Therefore, if Beth wants to sell her position in the swap, she should be paid $67.48.

Deferred Interest Rate Swaps

A deferred swap is a swap in which the payments are put off for a specified period in the future, but the swap rate is agreed upon today. The parties to the swap do not begin to exchange interest payments until some future date. For instance, a company wanting to enter a swap, but not wanting cash flows until a future period, may want to defer payment.

Example: Deferred Interest Swap

You are given that one-, two-, three- and four-year spot rates are 1%, 2%, 3%, and 4%, respectively.

Determine the swap rate for a two-year deferred, two-year interest rate swap.

Solution

Note that swap transactions start at the end of year 2. Thus, the timeline is as shown below:

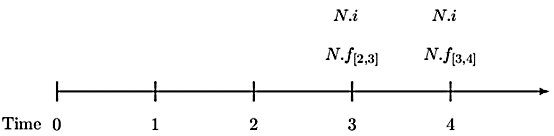
Since interest rates swaps are done in a fairway, the present value of the interest rate payments must be equal (Note that we are assuming unit notional amount). Thus the equation of value is given by:

$$ \begin{align*} &f_{\left[2,3\right]}\cdot v_3^3+f_{\left[3,4\right]}\cdot v_4^4=i\cdot v_3^3+i\cdot v_4^4\\ \Rightarrow i&=\frac{f_{\left[2,3\right]}\cdot v_3^3+f_{\left[3,4\right]}\cdot v_4^4}{v_3^3+v_4^4}\\ &=\frac{\left[f_{\left[2,3\right]}\cdot v_3^3\right]+\left[f_{\left[3,4\right]}\cdot v_4^4\right]}{v_3^3+v_4^4}\\ &=\frac{\left[v_2^2-v_3^3\right]+\left[v_3^3-v_4^4\right]}{v_3^3+v_4^4}\\ &=\frac{v_2^2-v_4^4}{v_3^3+v_4^4}=\frac{{(1.02)}^{-2}-{(1.04)}^{-4}}{{(1.03)}^{-3}+{(1.04)}^{-4}}=0.06009\approx6\% \end{align*} $$

Amortizing and Accreting Swaps

An amortizing swap is a swap where the notional value is declining over time. This swap would be useful to an investment property owner financing real estate with a mortgage tied to a variable interest rate.

An accreting swap is a swap where the notional value is growing over time. This allows an investor to match swap payments with its cash flow. For instance, a construction company can use this type of swap to finance a project in stages and lock in their funding costs by increasing the notional amount for increased cash flows, as more funding is needed for the next stage.

Example: Accreting Deferred Interest Rate Swaps

You are given that one-, two-, three- and four-year spot rates are 1%, 2%, 3%, and 4%, respectively.

Determine the swap rate for a two-year deferred, two-year interest rate swap, where the notional amount for year 3 is 100,000, and the notional amount for year 4 is 200,000.

Solution

From the information given, we have the following spot rates:

$$ s_1=0.01, s_2=0.02, s_3=0.03, s_4=0.04 $$

We are also given the notional amounts for year 3 and year four. That is, \(N_2\)=100,000 and \(N_3\)=200,000.

Consider the following timeline:

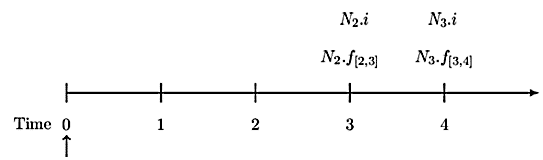
Since swaps are done in a fair way, the present value of the fixed interest rate payments must be equal to the present value of the variable interest rate payments. Denoting the fixed interest rate by \(i\), the equation of value must be:

$$ \begin{align*} & N_2\cdot\ f_{\left[2,3\right]}\cdot v_3^3+N_3\cdot f_{\left[3,4\right]}\cdot v_4^4=N_2\cdot i\cdot v_3^3+N_3\cdot i\cdot v_4^4\\ \Rightarrow i&=\frac{{N_2\cdot f}_{\left[2,3\right]}\cdot v_3^3+N_3\cdot f_{\left[3,4\right]}\cdot v_4^4}{N_2\cdot v_3^3+N_3\cdot v_4^4}\\ &=N_2\cdot [f_{[2,3]} \cdot v^3_3]+N_3 \cdot [f_{[3,4]} \cdot v^4_4]N_2 \cdot v^3_3+N_3 \cdot v^4_4\\ &=\frac{N_2\cdot\left[v_2^2-v_3^3\right]+N_3\cdot\left[v_3^3-v_4^4\right]}{N_2\cdot v_3^3+N_3\cdot v_4^4}\\ &=\frac{100000\cdot\left[\left(1.02\right)^{-2}-\left(1.03\right)^{-3}\right]+200000\cdot\left[\left(1.03\right)^{-3}-\left(1.04\right)^{-4}\right]}{100000\cdot\left(1.03\right)^{-3}+200000\cdot\left(1.04\right)^{-4}}\\ &=0.0635\approx6.35\% \end{align*} $$