Annuities/cash flows with non-continge ...
[vsw id=”vIQKtXXGqhc” source=”youtube” width=”611″ height=”344″ autoplay=”no”] AnalystPrep’s Actuarial Exams Preparation Materials For our question... Read More
[vsw id=”sFSv5ESO930″ source=”youtube” width=”611″ height=”344″ autoplay=”no”]
AnalystPrep’s Actuarial Exams Preparation Materials
For our question bank, study notes, quizzes, and all our video lessons: https://analystprep.com/shop/learn-practice-package-for-soa-exam-fm/
After completing this chapter, the candidate will be able to:
- Define and recognize the definitions of the following terms: principal, interest, term of loan, outstanding balance, final payment (drop payment, balloon payment), amortization.
- Calculate:
- The missing item, given any four of: term of loan, interest rate, payment amount, payment period, principal.
- The outstanding balance at any point in time.
- The amount of interest and principal repayment in a given payment.
- Similar calculations to the above when refinancing is involved.
A loan can be considered a compound interest transaction where the amount borrowed (Principal) is paid by regular payments at a fixed rate of interest for a predetermined period (term of the loan). The payment of the loan can sometimes involve drop payment, which is a short term payment (usually less than other payments) made at the end of the loan term. Also, a balloon payment is a payment made, usually a lump sum made towards the end of a loan. A balloon payment is usually higher than a periodic payment of a loan.
Individuals or companies raise funds by taking loans from financial institutions such as banks.
Let
\(\text{L}\) = The loan amount
\(\text{i}\) = The periodic effective interest rate on the loan
\(\text{n}\) = The number of periodic payments
\(\text{C}_\text{k}\)= The amountof the kth payment
Then if the loan is paid in n installments of annuity-immediate, the equation of value for a loan transaction is given by:
$$ \begin{align*} \text{C}_\text{k}\text{a}_{\overline{\text{n}}|}&=\text{L} \\ \Rightarrow\text{C}_\text{k}&=\frac{\text{L}}{\text{a}_{\overline{\text{n}}|}} \end{align*} $$
Note that for this case, we have level installments so that:
$$ \text{C}=\text{C}_1=\text{C}_2=\ldots\ \text{C}_\text{k}\ldots=\text{C}_\text{n} $$
The timeline for a loan is as shown below:
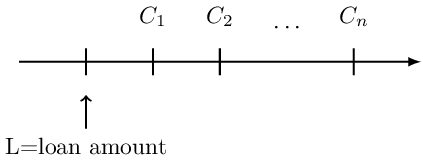
A cooperative society lends a farmer $1000, which is supposed to be paid at the end of each year for 3 years. The interest rate charged on loan is 10%.
Calculate the amount of each annual payment.
The equation of value is:
$$ Ca_{\overline{3}|}=1000\Rightarrow\ C=\frac{1000}{a_{\overline{3}|}}=\frac{1000}{2.486852}=402.1148 $$
Therefore, the farmer pays 402.11 at the end of the first, second, and third year. It is important to note that this amount covers the interest and capital repayment parts of the loan.
Consider a loan paid for n years and that the last payment of the loan exactly covers the capital outstanding and the interest due. Now, let
\(\text{I}_\text{k}\) = The amount of interest during the kth period
\(\text{P}_\text{k}\) = The capital (principal) repaid with kth payment
\(\text{B}_\text{k}\) = The outstanding balance immediately after the kth period payment, where \( \text{k} =0,1,2,\ldots \text{n} \)
Note that at any time \( \text{k}=1,2,\ldots,\text{n} , \)
$$ \text{C}_\text{k}=\text{I}_\text{k}+\text{P}_\text{k} $$
Moreover, the equation of value is given by:
$$ \text{L}=\text{B}_0=\text{C}_1\text{v}+\text{C}_2\text{v}^2+\ldots+\text{C}_\text{n}\text{v}^\text{n} $$
Which is intuitive.
Note also that:
$$ \text{I}_\text{k}=\text{iB}_{\text{k}-1} $$
So that:
$$ \begin{align*} \text{C}_\text{k}&=\text{I}_\text{k}+\text{P}_\text{k} \\ &=\text{iB}_{\text{k}-1}+\text{P}_\text{k} \end{align*} $$
\( \text{B}_\text{k} \) is the outstanding balance just after the \(\text{k}^\text{th}\) payment. But what about the balance before the kth payment? Denote the balance before the \(\text{k}^\text{th}\) and \( \text{B}_\text{k}^{\text{bef}} \). Intuitively, we can see that:
$$ \begin{align*} \text{B}_\text{k}^{\text{bef}}-\text{C}_\text{k}&=\text{B}_\text{k}\\ \Rightarrow \text{B}_\text{k}^{\text{bef}} & =\text{B}_\text{k}+\text{C}_ \text{k} \end{align*} $$
Another line of thought for calculating the balance before the payment is to go back one period to balance after \( (\text{k}-1)^\text{th} \) payment and accumulate it one period forward. Consider the following timeline:
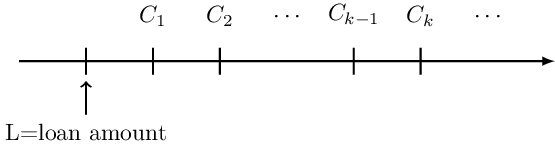
Therefore, the balance before the first payment is given by:
$$ \text{B}_\text{k}^{\text{bef}}=\text{B}_{\text{k}-1}\cdot\left(1+\text{i}\right) $$
Note also that:
$$ \text{L}=\sum_{\text{k}=1}^{\text{n}}\text{P}_\text{k} $$
Before we go into the methods of calculating loan balance, consider the example above (that of a farmer and cooperative society):
The initial amount of loan borrowed is $1000. The first payment of the loan is at time 1, and the interest due is \( {\textbf{0}}.{\textbf{1}}\times{\textbf{1000}}=${\textbf{100}}, \) which is the interest part of the payment \( {\textbf{402}}.{\textbf{1148}} \) so the capital repayment is \({\textbf{402}}.{\textbf{1148}}-{\textbf{100}}={\textbf{302}}.{\textbf{1148}}\). Therefore, the capital outstanding just after the first payment is \({\textbf{1000}}-{\textbf{302}}. {\textbf{1148}}={\textbf{697}}.{\textbf{8852}}\).
In the second year, the interesting part will be \( {\textbf{0}}.{\textbf{1}}\times{\textbf{697}}.{\textbf{8852}}={\textbf{69}}.{\textbf{78852}}\). The capital repayment part is \({\textbf{02}}.{\textbf{1148}}-{\textbf{69}}.{\textbf{78852}}={\textbf{332}}.{\textbf{32628}}\). So, the outstanding capital after the second payment is \({\textbf{697}}.{\textbf{8852}}-{\textbf{332}}.{\textbf{32628}}={\textbf{365}}.{\textbf{559}}\)
At the end of the loan term, the interest due will be \( {\textbf{0}}.{\textbf{1}}\times{\textbf{365}}.{\textbf{55892}}={\textbf{36}}.{\textbf{555892}}. \) So, the capital repayment is \({\textbf{402}}.{\textbf{1148}}-{\textbf{36}}.{\textbf{555892}}={\textbf{365}}.{\textbf{559}} \) and thus, the capital is exactly repaid at the last payment.
The above example should set a way of understanding how loans are transacted. It is worth noting that knowledge from the annuities is important here.
There are two methods in calculating the Loan Balance:
This approach can be described as “backward-looking.” It computes the capital outstanding as the accumulated amount of the loan at the time of valuation less the accumulated value of all regular payments (installments) that have been paid up to the time of valuation. That is:
$$ \text{B}_\text{k}=\text{AV}\left(\text{L}\right)-\text{AV}(\text{Past payments}) $$
Using the same notation defined above, we know that:
$$ \text{I}_\text{k}=\text{iB}_{\text{k}-1} $$
So that:
$$ \text{I}_1=\text{iB}_0, \text{I}_2=\text{iB}_2,\ldots $$
We also know that:
$$ \begin{align*} \text{C}_\text{k} & =\text{iB}_{\text{k}-1}+\text{P}_\text{k} \\ \Rightarrow \text{P}_\text{k} & =\text{C}_\text{k}-\text{iB}_{\text{k}-1} \end{align*} $$
So that the principal repaid at time \(\text{k}=1\) is:
$$ \text{P}_1=\text{C}_1-\text{iB}_0 $$
So the loan balance after the first payment will be:
$$ \begin{align*} \text{B}_1 & =\text{B}_0-\left(\text{C}_1-\text{iB}_0\right)\\ & =\text{B}_0\left(1+\text{i}\right)-\text{C}_1 \end{align*} $$
Intuitively, at any time \( \text{k} \geq 1 \) the interest due at that point will be:
$$ \text{I}_\text{k}=\text{iB}_{\text{k}-1} $$
And the capital repaid is:
$$ \text{P}_\text{k}=\text{C}_\text{k}-\text{iB}_{\text{k}-1} $$
So, the loan balance at any time k will be:
$$ \begin{align*} \text{B}_\text{k}&=\text{B}_{\text{k}-1}-\text{P}_\text{k}\\ &=\text{B}_{\text{k}-1}-\left(\text{C}_\text{k}-\text{iB}_{\text{k}-1}\right)\\ &=\text{B}_{\text{k}-1}+\text{iB}_{\text{k}-1}-\text{C}_\text{k}\\ &=\text{B}_{\text{k}-1}\left(1+\text{i}\right)-\text{C}_\text{k}\\ \therefore\text{B}_\text{k}&=\text{B}_{\text{k}-1}\left(1+\text{i}\right)-\text{C}_\text{k} \end{align*} $$
At this point, it is easy to see that, if we work from time k to time 0,
$$ \begin{align*} \text{B}_\text{k}&=\text{B}_{\text{k}-1}\left(1+\text{i}\right)-\text{C}_\text{k}\\ &={[\text{B}}_{\text{k}-2}\left(1+\text{i}\right)-\text{C}_{\text{k}-1}](1+\text{i}) -\text{Ck} \\ &=\text{B}_{\text{k}-2}\left(1+\text{i}\right)^2-\text{C}_{\text{k}-1}\left(1+\text{i}\right)-\text{C}_\text{k}\\ &=\text{B}_0\left(1+\text{i}\right)^\text{k}-\left[\text{C}_1\left(1+\text{i}\right)^{\text{k}-1}+\text{C}_2\left(1+\text{i}\right)^{\text{k}-2}+\ldots+\text{C}_{\text{k}-1}\left(1+\text{i}\right)+\text{C}_\text{k}\right] \end{align*} $$
So,
$$ \text{B}_\text{k}=\text{B}_{0}\left(1+\text{i}\right)^\text{k}-\text{C}_\text{k}\text{s}_{\overline{\text{k}}|} $$
Which completes the definition of calculating loan balances using the retrospective method.
A cooperative society lends a farmer $1000, which is supposed to be paid at the end of each year for 3 years. The interest rate charged on loan is 10%.
Calculate the capital outstanding after the first payment using the retrospective method.
Using the retrospective method, the loan is:
$$ \text{B}_\text{k}=\text{B}_0\left(1+\text{i}\right)^\text{k}-\text{C}\text{s}_{\overline{\text{k}}|} $$
We need:
$$ \text{B}_1=\text{B}_0\left(1+\text{i}\right)^1-\text{C}\text{s}_{\overline{1}|} $$
Now, let the annual payments be $C. Then the equation of value is:
$$ \begin{align*} \text{Ca}_{\overline{3}|}&=1000\Rightarrow\text{C}=\frac{1000}{\text{a}_{\overline{3}|}}=\frac{1000}{2.486852}=402.1148 \\ \Rightarrow\text{B}_1 & =1000\left(1.1\right)^1-402.1148\left(1\right) \\ &=1100-402.1148=697.885 \end{align*} $$
This method calculates the loan balance as the present value of the future payments that will be made at a given interest rate within the term of the loan. That is,
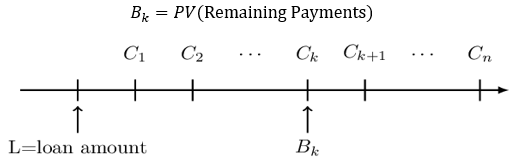
Where \(\text{B}_\text{k}\)= balance just after the \(\text{k}^\text{th}\) payment.
Consider a loan transaction at time n (end of the loan term). Intuitively, when the last payment (consisting of the principal repayment and interest), the loan is exactly repaid. The final payment \(\text{C}_\text{n}\) must cover the principal repayment after the repayment at time n-1 and the interest due on that capital. Therefore, at the last payment:
$$ \text{I}_\text{n}=\text{iB}_{\text{n}-1} $$
And
$$ \text{P}_\text{k}=\text{B}_{\text{n}-1} $$
So that
$$ \begin{align*} \text{C}_\text{n}&=\text{I}_\text{n}+\text{P}_\text{n}=\text{iB}_{\text{n}-1}+\text{B}_ {\text{n}-1}\\ &=\text{iB}_{\text{n}-1}+\text{B}_{\text{n}-1}\\ &=\left(1+\text{i}\right)\text{B}_{\text{n}-1} \\ \Rightarrow\text{B}_{\text{n}-1}&=\text{v}\text{C}_\text{n} \end{align*} $$
From the last expression, it is easy to see that the capital outstanding at time n-1 is equivalent to the present value of the future payment at time n.
From the above result, we are comfortable to see that, at any time k+1 where \( \text{k}\le \text{n}-2 \) , the principal repaid is \(\text{B}_\text{k}-\text{B}_{\text{k}+1}\) so that the payment \( \text{C}_{\text{k}+1}\) is:
$$ \begin{align*} \text{C}_{\text{k}+1}&=\text{iB}_\text{k}+(\text{B}_\text{k}-\text{B}_{\text{k}+1})\\ \Rightarrow \text{B}_\text{k}&=\left(\text{B}_{\text{k}+1}+\text{C}_{\text{k}+1}\right)\text{v} \end{align*} $$
Maintaining this line of thought, it implies that:
$$ \text{B}_{\text{k}+1}=\left(\text{B}_{\text{k}+2}+\text{C}_{\text{k}+2}\right)\text{v} $$
Therefore, working forwardly, while substituting for \(\text{B}_{\text{k}+\text{r}} \) until we reach \(\text{B}_\text{n}=0\) ,we have:
$$ \begin{align*} \text{B}_\text{k} & =\left(\text{B}_{\text{k}+1}+\text{C}_{\text{k}+1}\right)\text{v} \\ & =\left[\left(\text{B}_{\text{k}+2}+\text{C}_{\text{k}+2}\right)\text{v}+\text{C}_{\text{k}+1}\right]\text{v}=\text{C}_{\text{k}+1}\text{v}+\text{C}_{\text{k}+2}\text{v}^2+\text{B}_{\text{k}+2}\text{v}^2\\ & =\text{C}_{\text{k}+1}\text{v}+\text{C}_{\text{k}+2}\text{v}^2+\text{C}_{\text{k}+3}\text{v}^3+\text{B}_{\text{k}+3}\text{v}^3 \\ & =\vdots\\ & =\text{C}_{\text{k}+1}\text{v}+\text{C}_{\text{k}+2}\text{v}^2+\text{C}_{\text{k}+3}\text{v}^3+\ldots \text{C}_\text{n}\text{v}^{\text{n}-\text{k}} \end{align*} $$
If we assume that periodic payments are constant so that:
$$ \text{C}_{\text{k}+1}=\text{C}_{\text{k}+2}=\text{C}_{\text{k}+3}=\ldots=\text{C}_\text{n}=\text{C} $$
Then,
\( \text{B}_\text{k}=\text{Ca}_{\overline{\text{n}-\text{k}}|} \)
Which completes the definition of the prospective method of calculating the loan balance.
A cooperative society lends a farmer $1000, which is supposed to be paid at the end of each year for 3 years. The interest rate charged on loan is 10%.
Calculate the capital outstanding after the first payment using the prospective method.
Let the annual payments be $C. The equation of value is therefore:
$$ \text{C}\text{a}_{\overline{3}|}=1000\Rightarrow\text{C}=\frac{1000}{\text{a}_{\overline{3}|}}=\frac{1000}{2.486852}=402.1148 $$
We know that using a prospective method:
$$ \text{B}_\text{k}=\text{Ca}_{\overline{\text{n}-\text{k}}|} $$
We need:
$$ \text{B}_1=\text{Ca}_{\overline{3-1}|}=402.1148a_{\overline{3-1}@\text{i}=10\%|}=697.885 $$
It is easy to show that both methods lead to the same result. The retrospective method is given by:
$$ \begin{align*} \text{B}_0\left(1+\text{i}\right)^\text{k}-\text{C}\text{s}_{\overline{\text{k}}|}&=\text{C}\text{a}_{\overline{\text{n}}|}\left(1+\text{i}\right)^\text{k}-\text{C}\text{Xs}_{\overline{\text{k}}|}( \text{since } \text{B}_0=\text{a}_{\overline{\text{n}}|}) \\ &=\text{C}\left[\frac{1-\text{v}^\text{n}}{\text{i}}\left(1+\text{i}\right)^\text{k}-\frac{\left(1+\text{i}\right)^\text{k}-1}{\text{i}}\right](\text{Apply simple Algebra} )\\ &=\text{C}\left[\frac{1-\text{v}^{\text{n}-\text{k}}}{\text{i}}\right] \\ &=\text{C}\textbf{a}_{\overline{\textbf{n}-\textbf{k}}|}@{\textbf{i}} \end{align*} $$
The last expression is simply the formula for calculating the loan balance prospectively. So,
$$ \text{B}_0\left(1+\text{i}\right)^\text{k}-\text{Cs}_{\overline{\text{k}}|}=\text{Ca}_{\overline{\text{n}-\text{k}}|}@\text{i} $$
Recall that the interest paid during the kth period is given by:
$$ \text{I}_\text{k}=\text{iB}_{\text{k}-1} $$
Also, recall that the amount of principal repaid with kth payment is given by:
$$ \text{P}_\text{k}=\text{C}_\text{k}-\text{I}_\text{k} $$
And that:
$$ \text{L}=\sum_{\text{k}=1}^{\text{n}}\text{P}_\text{k} $$
Now assume that we want to calculate the amount of principal repaid from time t=k to time t=m. It is given by:
$$ \sum_{\text{j}=\text{k}+1}^{\text{m}}\text{P}_\text{j}=\text{B}_\text{k}-\text{B}_\text{m} $$
The formula above implies that the capital repaid between the times k and m is simply equivalent to the difference between the balance at times k and m.
Moreover, the amount of interest paid between the times k and m is given by:
$$ \begin{align*} \sum_{\text{j}=\text{k}+1}^{\text{m}}\text{I}_\text{j}&=\sum_{\text{j}=\text{k}+1}^{\text{m}}\text{C}_\text{j}-\sum_{\text{j}=\text{k}+1}^{\text{m}}\text{P}_\text{j}\\ \quad \quad &=\sum_{\text{j}=\text{k}+1}^{\text{m}}{[\text{C}}_\text{j}-(\text{B}_\text{k}-\text{B}_\text{m})] \\ \therefore\sum_{\text{j}=\text{k}+1}^{\text{m}}\text{I}_\text{j}&=\sum_{\text{j}=\text{k}+1}^{\text{m}}{[\text{C}}_\text{j}-(\text{B}_\text{k}-\text{B}_\text{m})] \end{align*} $$
The formula above simply means that the interest between times k and m is equivalent to the sum of the payments after time k up to and including time m LESS the amount of principal repaid from time k to time m.
An investor takes a loan of $32,000 from a bank, which is repaid by 10 equal payments made at the end of each year. The effective rate of interest is 4%.
Calculate the interest due to the 4th payment.
Let the annual payment be $C. We have the following formula:
$$ \text{Ca}_{\overline{10}|}=32000\Rightarrow\text{C}=\frac{32000}{\text{a}_{\overline{10}|}}=\frac{32000}{8.110896}=3945.3102 $$
We need to find the loan balance after the 3rd payment. That is:
$$ \begin{align*} \text{B}_\text{k} & =\text{Ca}_{\overline{\text{n}-\text{k}}|} \\ \Rightarrow{\text{B}}_3 & =\text{X}\text{Ca}_{\overline{7}|} \\ & =3945.3102\times6.0021=23679.9675 \end{align*} $$
So, the interest element of the 4th element is:
$$ \begin{align*} \text{I}_\text{k} & ={\text{iB}}_{\text{k}-1} \\ \Rightarrow\text{I}_4 & =\text{iB}_3=0.04\times23679.9675=947.1987 \end{align*} $$
A loan of 100,000 at a monthly effective interest rate of 0.5% is repaid with regular monthly payments of 1000 and a final smaller payment one month after the last regular payment.
Note that we are not given the number of payments, so it will be appropriate to use the retrospective method. We know that for the retrospective method, the outstanding balance is given by:
$$ \begin{align*} {\text{B}}_\text{k}&=\text{AV}\left(\text{L}\right)-\text{AV}(\text{Past Payments})\\ &=\text{B}_0\left(1+\text{i}\right)^\text{k}-\text{Cs}_{\overline{\text{k}}|} \end{align*} $$
In this case, we need:
$$ \begin{align*} \text{B}_{50}&=\text{B}_0\left(1+\text{i}\right)^{50}-\text{Cs}_{\overline{50}|}\\ &=100000\left(1.005\right)^{50}-1000s_{\overline{50}|0.005}\\ &=71,677.42 \end{align*} $$
We need first to calculate the number of payments. The equation of value is given by:
$$ 100000=1000\text{a}_{\overline{\text{n}|}0.005} $$
Now using a financial calculator with parameters: PV=-100,000, I/Y=0.5, PMT=1000 and FV=0, we have:
$$ n=138.9758 $$
Denoting the drop payment by Y, then the timeline of the loan above is therefore given by:
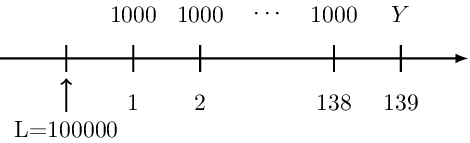
Intuitively, to calculate the drop payment Y, we need to compute the balance after the 138th payment and then accumulate it by one period. That is:
$$ \text{Y}=\text{B}_{138}\cdot(1.005) $$
Using the retrospective method, we have that:
$$ \begin{align*} \text{B}_{138}&=100000\left(1.005\right)^{138}-1000s_{\overline{138}|0.005}\\ &=970.93 \\ \Rightarrow\text{Y} & =970.93\cdot\left(1.005\right)=975.78 \end{align*} $$
Assume now we knew everything about the loan. That is, n=139 and that the drop payment is 975.78, and we wish to calculate the outstanding just after the 50th payment. Now, we know that calculating the outstanding balance using the prospective method is given by:
$$ \text{B}_\text{k}=\text{Ca}_{\overline{\text{n}-\text{k}}|} $$
So, in this case, we have:
$$ \text{B}_{50}=1000\text{a}_{\overline{88}|0.005}+975.78\text{v}^{89} $$
Using a financial calculator, you should get
$$ \text{B}_{50}=71,677.42 $$
Which is the same result as in the retrospective case.
A loan of 500,000 at an annual effective interest rate of 6% is repaid with annual payments. The first payment is 20,000, and subsequent payments are 5000 more than their preceding payments.
Determine the outstanding balance immediately after the 10th payment.
The timeline for the loan is given by:
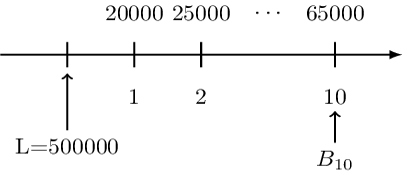
Just like in the annuities, we can rearrange the payments as shown below:
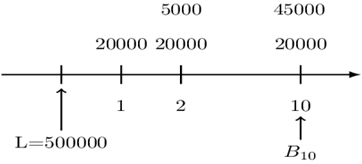
Now using the retrospective method, we have:
$$ \begin{align*} \text{B}_{10}&=500000\left(1.06\right)^{10}-\text{AV}\left(\text{Past Payments} \right)\\ &=500000\left(1.06\right)^{10}-\left(15000\text{s}_{\overline{10}|}+5000\left(\text{Is}\right)_{\overline{10}|}\right)\\ &=500000\left(1.06\right)^{10}-15000s_{\overline{10}|}-5000\left(Is\right)_{\overline{10}|}\\ &=366,741.70 \end{align*} $$
Some loans are paid half-yearly, quarterly, or monthly. There are no new rules or principles, but one should be keen when calculating the interest due at any installment.
For instance, a loan is repaid by level amounts $X installments payable m-thly, then the equation of value will be given by:
$$ \text{L}_0=\text{Ca}_{\overline{\text{n|}}}^{\left(\text{m}\right)} $$
An investor borrows a loan of $9000, which is payable by equal monthly installments of $Y for the next 3 years. The effective yearly rate of interest charged on loan is 18.5%.
Calculate Y.
The equation of value is:
$$ \begin{align*} 9000 & =12\text{Y} {\text{a}_{\overline{3}|}^{\left(12\right).}}=12\text{Y}\left[\frac{1-\text{v}3}{\text{i}{\left(12\right)}}\right]\\ \\ \Rightarrow \text{Y}=\frac{9000\text{i}^{\left(12\right)}}{12(1-\text{v}^3)} & =\frac{9000\times12({1.185}^\frac{1}{12}-1)}{12(1-{1.185}^{-3})}=$320.13 \end{align*} $$
A 10-year loan at a quarterly effective interest rate of 2% is repaid with quarterly payments. The first payment is 1000, and subsequent payments are 2% less than their preceding payments.
Determine the outstanding balance immediately after the 25th payment.
The timeline of the loan payments are is given below:
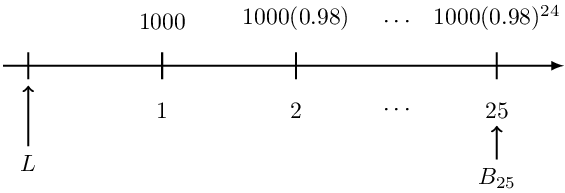
Since we do not know the loan amount, the prospective method of calculating the outstanding loan is appropriate here. Now if we rewrite our timeline, we have
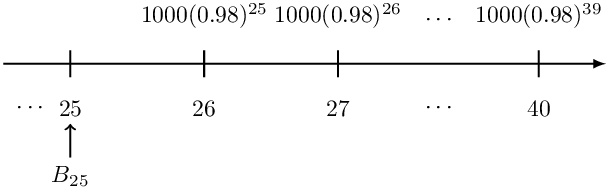
So using the prospective method, the loan outstanding immediately after the first payment is:
$$ \begin{align*} \text{B}_{25}&=1000\left(0.98\right)^{25}\text{v}+1000\left(0.98\right)^{26}\text{v}^2+\cdots+1000\left(0.98\right)^{40}\text{v}^{15}\\ &=1000\left(0.98\right)^{25}\text{v}\left[1+0.98\text{v}\cdots+\left(0.98\right)^{14}\text{v}^{14}\right]\\ &=\frac{1000{(.98)}^{25}}{1.02}\left[1+\frac{0.98}{1.02}+\cdots+\left(\frac{0.98}{1.02}\right)^{14}\right] \end{align*} $$
Note \( \frac{0.98}{1.02} \).
$$ \frac{0.98}{1.02}=\frac{1}{1+\text{j}} \\ 1+\frac{0.98}{1.02}+\cdots+\left(\frac{0.98}{1.02}\right)^{14}=1+\left(1+\text{j}\right)^{-1}+ \cdots+\left(1+\text{j}\right)^{-14}={\ddot{\text{a}}_{\overline{15}|@\text{j}}} $$
Where
$$ \text{j}={\frac{1.02}{0.98}-1}=0.04082 \\ \therefore\text{B}_{25}=\frac{1000{(.98)}^{25}}{1.02}\cdot\ddot{\text{a}}_{\overline{15}|@\text{j}}=6807.57 $$
A 10-year loan of 200,000 at an annual effective interest rate of 5% is repaid with annual payments. Each of the first 9 payments equals 120% of the interest due at the time of the payment.
The timeline of the loan described in the question is given below: 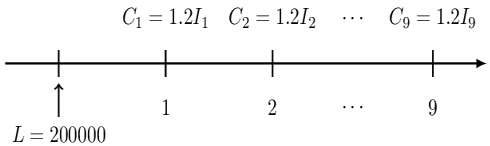
We need to try and find a pattern of balances at each payment period. Now, notice that:
$$ {\text{L}=\text{B}}_0 $$
Using the fact that:
$$ \text{B}_\text{k}=\text{B}_{\text{k}-1}-\text{P}_\text{k} $$
We have:
$$ \text{B}_1=\text{B}_0-\text{P}_1 $$
But
$$ \text{P}_1=\text{C}_1-\text{I}_1=1.2\text{I}_1-\text{I}_1=0.2\text{I}_1 $$
And
$$ \begin{align*} \text{I}_1&=\text{i}.\text{B}_0=0.05\text{B}_0\\ \Rightarrow \text{B}_1&=\text{B}_0-0.2\text{I}_1\\ &=\text{B}_0-0.2\left(0.05\text{B}_0\right)\\ &=\text{B}_0-0.01\text{B}_0\\ &=0.99\text{B}_0 \end{align*} $$
Similarly for \(\text{B}_2 \), we have:
$$ \begin{align*} \text{B}_2&=\text{B}_1-\text{P}_2\\ &=\text{B}_1-\left(1.2\text{I}_2-\text{I_2}\right)\\ &=\text{B}_1-0.2\text{I}_2\\ &=\text{B}_1-0.2{(0.05\text{B}}_1)=0.99\text{B}_1 \end{align*} $$
But
$$ \begin{align*} \text{B}_1&=0.99B_0 \\ \Rightarrow \text{B}_1&={(0.99)}^2\text{B}_0 \end{align*} $$
We can see that the pattern of the loan balances is as follows:
$$ \begin{align*} \text{B}_1&=0.99\text{B}_0\\ \text{B}_1&=\left(0.99\right)^2\text{B}_0\\ \vdots\\ \text{B}_9&=\left(0.99\right)^9\text{B}_0 \end{align*} $$
We know that \( \text{L}=\text{B}_0 \) so that:
$$ \text{B}_9={(0.99)}^9\cdot200000=182,703.45\ $$
To calculate the value of the balloon payment, we just need to accumulate the balance just after the 9th payment one period forward (accumulation of the 9th payment) which is basically the 10th payment \( \text{C}_{10}\). Therefore, the balloon payment is:
$$ \begin{align*} \text{C}_{10}&=\text{B}_9\left(1+\text{i}\right)=182,703.45\left(1.05\right)\\ &=191,838.62 \end{align*} $$
A 5-year loan of 20,000 is repaid with annual payments. Each payment consists of a principal payment of 4000, plus interest on the unpaid balance using 6% annual effective. The lender reinvests each payment in an account that pays 5% annual effective.
Consider the following timeline: 
Note the question says, “…principal payment of 4000, plus interest on the unpaid balance using 6% annual effective.” So,
$$ \begin{align*} \text{P}_\text{k}&=4,000 \\ \text{C}_\text{k}&=\text{i}.\text{B}_{\text{k}-1}+\text{P}_\text{k}\\ \text{C}_1&=0.06\times20,000+4,000=5,200 \end{align*} $$
The second period, the balance is now 20,000-4,000=16,000, so that:
$$ \text{C}_2=0.06\times16,000+4,000=4,960 $$
The above analogy continues up to the fifth payment so that payments that the lender will receive at each period is shown below:
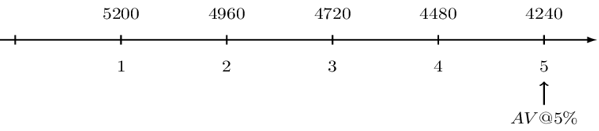
The lender reinvests the payments at a 5% effective interest rate, the value of the investment at year 5 is simply the accumulated value of these payments at the end of year 5. Note that the payments can be rearranged as:

So that the accumulated value of the payments is given by:
$$ \text{AV}=4000\text{s}_{\overline{5}|0.05}+240\left(\text{Ds}\right)_{\overline{5}|0.05}=26,210.25 $$
From the lender’s perspective, the lender gives out 20,000 at time 0 and receive 26,210.25 at time 5. Therefore, the yield rate is simply the annual effective interest rate that makes the 20,000 and 26,210.25 equivalent. Consider the following timeline: 
So, the equation of value is:
$$ \begin{align*} 20000{(1+\text{i})}^5&=26210.25 \\ \Rightarrow\text{i}&=5.56\% \end{align*} $$
If a loan is paid using the amortization method, then each annual payment (installment) is first used to cover for the interest incurred and the other part to decrease the principal.
To see this clearly, let L be the amount of the loan. Then the interest element of the first payment is iL. But \( \text{L}=\text{a}_{\overline{\text{n}}|}@\text{i} \) where i is the interest charged on loan. So, the interest element of the first payment is simplified to:
$$ \text{iL}=\text{ia}_{\overline{\text{n}}|}=\text{i}\left[\frac{1-\text{v}^\text{n}}{\text{i}}\right]=1-\text{v}^\text{n} $$
From the formula above it is easy to see that \( 1-\text{v}^\text{n} \) is the amount used to offset the interest due and thus the loan principal is reduced by \( \text{v}^\text{n} \) so that the outstanding loan balance is given by:
$$ \begin{align*} \text{a}_{\overline{\text{n}}|}-\text{v}^\text{n} & =\left[\frac{1-\text{v}^\text{n}}{\text{i}}\right]-\text{v}^\text{n} \\ & =\frac{1-\text{v}^\text{n}\left(1+i\right)}{\text{i}}\\ & =\frac{1-\text{v}^{\text{n}-1}}{\text{i}}=\text{a}_{\overline{\text{n}-1}|}@\text{i} \end{align*} $$
Using the above result, we can contract the amortization schedule or sometimes referred to as the loan schedule, as shown below:
$$ \begin{array}{c|c|c|c|c} {\text{Time} } & {\text{Installment} } & {\text{Interest} \\ \text{payment} } & {\text{Principal}\\ \text{payment} } & {\text{Outstanding} \\ \text{Balance} } \\ \hline {0} & {} & {} & {} & {\text{a}_{\overline{\text{n}}|}} \\ \hline {1} & {1} & { \text{ia}_{\overline{\text{n}}|}=1-\text{v}^\text{n} } & { \text{v}^\text{n} } & { \text{a}_{\overline{\text{n}}|}-\text{v}^\text{n} \\ =\text{a}_{\overline{\text{n}-1}|} } \\ \hline {\vdots} & {\vdots} & {\vdots} & {} & {\vdots} \\ \hline {\text{k}} & {1} & { \text{ia}_{\overline{\text{n}-\text{k}+1}|}\\=1-\text{v}^\text{n} } & { \text{v}^{\text{n}-\text{t}+1} } & { \text{a}_{\overline{\text{n}-\text{k}+1}|}\\-\text{v}^{\text{n}-\text{t}+1} \\=\text{a}_{\overline{\text{n}-\text{k}}|} } \\ \hline {\vdots} & {\vdots} & {\vdots} & {\vdots} & {\vdots} \\ \hline \text{n} & {1} & {\text{ia}_{\overline{1}|}=1-\text{v} } & { \text{v} } & { \text{a}_{\overline{1}|}-\text{v}=0 } \\ \hline \text{Total} & \text{N} & {\text{n}-\text{a}_{\overline{\text{n}}|}} & { \text{a}_{\overline{\text{n}}|} } & {} \end{array} $$
A 4-year loan of 1000 at an annual effective interest rate of 4% is repaid with level annual payments.
Determine the amount of each payment.
Let C be the amount of each payment. The timeline for the loan is given below:
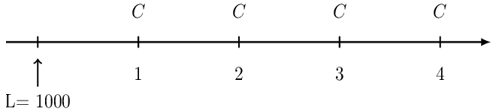
We need to find the annual payment (installment). From the information given, the equation of value is:
$$ \begin{align*} \text{Ca}_{\overline{4}|}@4\% & = 1000 \\ \Rightarrow \text{C}& =\frac{1000}{\text{a}_{\overline{4}|}}=275.49 \end{align*} $$
Now, study the table below:
$$ \begin{array}{c|c|c|c|c} {\text{Time} \\ \textbf{k} } & {\text{Payment} \\ \textbf{C} } & {\text{Interest Paid} \\ \textbf{I}_\textbf{k} } & {\text{Principal Repaid}\\ \textbf{P}_\textbf{k}} & {\text{Outstanding} \\ \textbf{B}_\textbf{k} } \\ \hline {0} & {-} & {-} & {-} & {1000} \\ \hline {1} & {275.49} & { {=0.04×1000} \\ {=40} } & { {=275.49-40} \\ {=235.49} } & { {=1000-235.49} \\ {=764.51} } \\ \hline {2} & {275.49} & { {=0.04×764.51} \\ {=30.58} } & { {=275.49-30.58} \\ {=244.91} } & { {=764.51-244.91} \\ {=519.60} } \\ \hline {3} & {275.49} & { {=0.04×519.60} \\ {=20.78} } & { {=275.49-20.78} \\ {=254.71} } & { {=519.60-254.71} \\ {=264.89} } \\ \hline {4} & {275.49} & { {=0.04×264.89} \\ {=10.60} } & { {=275.49-10.60} \\ {=264.89} } & { {=264.89-264.89} \\ {=0} } \\ \hline \text{Total} & \textbf{1143.15} & \textbf{143.1554 } & { 1000 } & {} \end{array} $$
The sum of the principal repaid is equivalent to the loan amount. Moreover, note that \(\text{P}_\text{k}\) is a geometric sequence with common ratio 1+i. That is,
$$ \text{P}_2=\text{P}_1\cdot(1+\text{i}), \text{P}_3=\text{P}_1\cdot{(1+\text{i})}^2, \text{P}_4=\text{P}_1\cdot{(1+\text{i})}^3 $$
Notice from the above the table:
$$ \frac{244.91}{235.49}=\frac{254.71}{244.91}=\frac{264.89}{254.71}=1.04 $$
Generally, we have:
$$ \text{L}=\text{C}\cdot\text{a}_{\overline{\text{n}}|} $$
$$ \begin{align*} \text{L}&=\sum \text{P}_\text{k}=\text{P}_1+\text{P}_2+\ldots+\text{P}_\text{n}\\ &=\text{P}_1\left(1+ \left(1+\text{i}\right)+\ldots+\left(1+\text{i}\right)^{\text{n}-1}\right)\\ &=\text{P}_1\cdot\text{s}_{\overline{\text{n|}}} \end{align*} $$
Also note that:
$$ \begin{align*} \text{L}&=\text{P}_1\cdot \text{s}_{\overline{\text{n}}|}=\text{C}\cdot \text{a}_{\overline{\text{n}}|} \\ \Longrightarrow \text{C}&=\text{P}_1\cdot{(1+\text{i})}^\text{n} \end{align*} $$
\( \left\{ \text{P}_1,\text{P}_2,\ldots,\text{P}_\text{n} \right\} \) is a geometric sequence with common ratio \(\text{r}=1+\text{i}\).
$$ \text{B}_\text{k}=\text{C}\cdot \text{a}_{\overline{\text{m}-\text{k}}|}+\text{B}_\text{m}\cdot\text{v}^{\text{m}-\text{k}} \forall \text{ k}<\text{m} $$
We can calculate the above equation using a one-step TVM calculation with the parameters indicated below:
$$ \underbrace { { \text B }_{\text k } }_{ \text{PV} } =\text C\cdot \underbrace { \text a_{ \overline { \text m-{\text k}| } } }_{\text N } +\underbrace { {\text B }_{\text m } }_{\text {FV} } \cdot {\text v }^{ {\text m-{\text k} } } $$
Note that \(N=m-k\).
A 3-year loan of 50,000 is repaid with level monthly payments. The amount of interest paid in the 21st payment equals 1.96 times the amount of interest paid in the 29th payment.
Determine the amount of monthly payments.
From the information given in the question, it is true that:
$$ \text{I}_{21}=1.96\text{I}_{29} $$
But,
$$ \text{I}_{21}=\text{iB}_{20} $$
And
$$ \begin{align*} \text{I}_{29}&=\text{iB}_{28} \\ \Rightarrow\text{iB}_{20}&=1.96\text{iB}_{28} \\ \therefore \text{B}_{20}&=1.96\text{B}_{28} \end{align*} $$
Using the prospective method, we know that:
$$ \text{B}_{20}=\text{Ca}_{\overline{16}|} $$
And
$$ \text{B}_{20}=\text{Ca}_{\overline{16}|} $$
So,
$$ \begin{align*} \text{Ca}_{\overline{16}|}&=1.96\cdot \text{Ca}_{\overline{8}|} \\ \therefore \text{a}_{\overline{16}|}&=1.96\cdot \text{a}_{\overline{8}|} \end{align*} $$
Note that we write \( \text{a}_{\overline{16}|} \) as:
$$ \text{a}_{\overline{16}|}=\text{a}_{\overline{8}|}+\text{v}^8\text{a}_{\overline{8}|}=\text{a}_{\overline{8}|}(1+\text{v}^8) $$
Therefore, we can write \( \text{a}_{\overline{16}|}=1.96\cdot \text{a}_{\overline{8}|} \) as:
$$ \begin{align*} \text{a}_{\overline{16}|}&=1.96\cdot \text{a}_{\overline{8}|}\\ \text{a}_{\overline{8}|}\cdot\left(1+\text{v}^8\right)&=1.96.\text{a}_{\overline{8}|}\\ \therefore\left(1+\text{v}^8\right)&=1.96\\ \Rightarrow \text{v}^8&=0.96 \end{align*} $$
Now using a financial calculator, we get:
$$ \therefore \text{i}=0.0051 $$
At this point, we can solve the monthly payment using the equation of value:
$$ \begin{align*} 50000&=\text{Ca}_{\overline{36}|\text{i}=0.0051}\\ \Rightarrow \text{C}&=1,524.25 \end{align*} $$
A 30-year mortgage of 300,000 at a nominal rate of 3.6% compounded monthly is repaid with level monthly payments.
Determine the amount of interest paid during the second 10-year period.
We are given that the nominal interest rate is 3.6% so that the monthly effective interests rate is:
$$ \text{meir}=\frac{0.036}{12}=0.003 $$
Now, we need to calculate the monthly payment. The equation of value is:
$$ 300000=\text{Ca}_{\overline{360}|0.003} \\ \Rightarrow \text{C}=1363.94 $$
Note that the second 10-year period extends from time k=120 to time m=240. First, we need to calculate the amount of payments in the second 10-year period, which is given by:
$$ =120\cdot \text{C}=163,672 $$
Now, the amount of the principal repaid is given by:
$$ \text{Total Amount of Principal Repaid}=\text{B}_{120}-\text{B}_{240} $$
Now using the prospective method (you can also use the retrospective method):
$$ \begin{align*} \text{B}_{120}&=\text{C}\cdot \text{a}_{\overline{240}|}=1363.94.\text{a}_{\overline{240}|}=233,107.0451 \\ \text{B}_{240}&=\text{C}\cdot \text{a}_{\overline{120240}|}=1363.94.\text{a}_{\overline{120240}|}=137,279.0629 \end{align*} $$
(Using your financial calculator at this point save time.)
Therefore,
$$ \text{Total Amount of Principal Repaid}=233107.0451-137279.0629=95,828. $$
So the amount of interest in the “second 10-year period” is the difference between the amount of payments paid and the amount of principal paid:
$$ \therefore \text{Total Amount of Interest Paid}=163672-95828=67844 $$
A loan at 5% annual effective is repaid with level annual payments at the end of each year for 2n years. The amount of principal repaid in the \( \text{n}^{\text{th}} \) payment is 171. The balance immediately after the next to last payment is 476.
Determine the amount borrowed.
From the information given in the question, we know that:
\( \text{P}_\text{n}=171, \text{B}_{2\text{n}-1}=476 \)
We also know that:
$$ \text{B}_{2\text{n}}=0 $$
So that:
$$ \begin{align*} \text{P}_{2\text{n}}&=\text{B}_{2\text{n}-1}-\text{B}_{2\text{n}}=476-0=476 \\ \Rightarrow \text{P}_{2\text{n}}&=476 \end{align*} $$
Now, we can relate \(\text{P}_\text{n}\) and \(\text{P}_{2\text{n}} \) by the following equation:
$$ \begin{align*} \text{P}_{2\text{n}}&=\text{P}_\text{n}{(1+\text{i})}^\text{n} \\ \Rightarrow 476&=171{(1.05)}^\text{n} \\ \therefore{(1.05)}^\text{n}&=\frac{476}{171}\Rightarrow \text{n}=20.98280084\approx21 \end{align*} $$
Recall that, the amount of the loan L is given by:
$$ \text{L}=\sum_{\text{ji}=1}^{\text{n}} {\text{P}_\text{j}} $$
Where \(\text{P}_\text{j}\) is principal repayments in each period. However, in this case, we have 2n payments so that:
$$ \text{L}=\sum_{\text{ji}=1}^{2\text{n}}\text{P}_\text{j} $$
Also, notice that we are dealing with level payments so that the principal payments are in the form of a geometric annuity and thus the equation above can be written as:
$$ \text{L}=\text{P}_1\cdot \text{s}_{\overline{2\text{n}}|} $$
Now, notice that:
$$ \begin{align*} \text{P}_{21}&=\text{P}_1\left(1+\text{i}\right)^{20}\\ \Rightarrow171&=\text{P}_1\left(1.05\right)^{20}\\ \therefore \text{P}_1&=64.45 \end{align*} $$
And thus the amount of the loan is given by:
$$ \therefore \text{L}=64.45\cdot \text{s}_{\overline{42}|}=8715.68 \quad (\text{Using a Financial Calculator}) $$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.