Key Properties of the Normal Distribution
A random variable is said to have the normal distribution (Gaussian curve) if its values make a smooth curve that assumes a “bell shape.” A normal variable has a mean “μ,” pronounced as “mu,” and a standard deviation “σ,” pronounced…
Univariate vs. Multivariate Distributions and the Role of Correlation in the Multivariate Normal Distribution
Univariate and multivariate normal distributions are very robust and useful in most statistical procedures. Understanding their form and function will help you learn a lot about most statistical routines.
Confidence Intervals
A confidence interval (CI) gives an “interval estimate” of an unknown population parameter such as the mean. It gives us the probability that the parameter lies within the stated interval (range). The precision or accuracy of the estimate depends on…
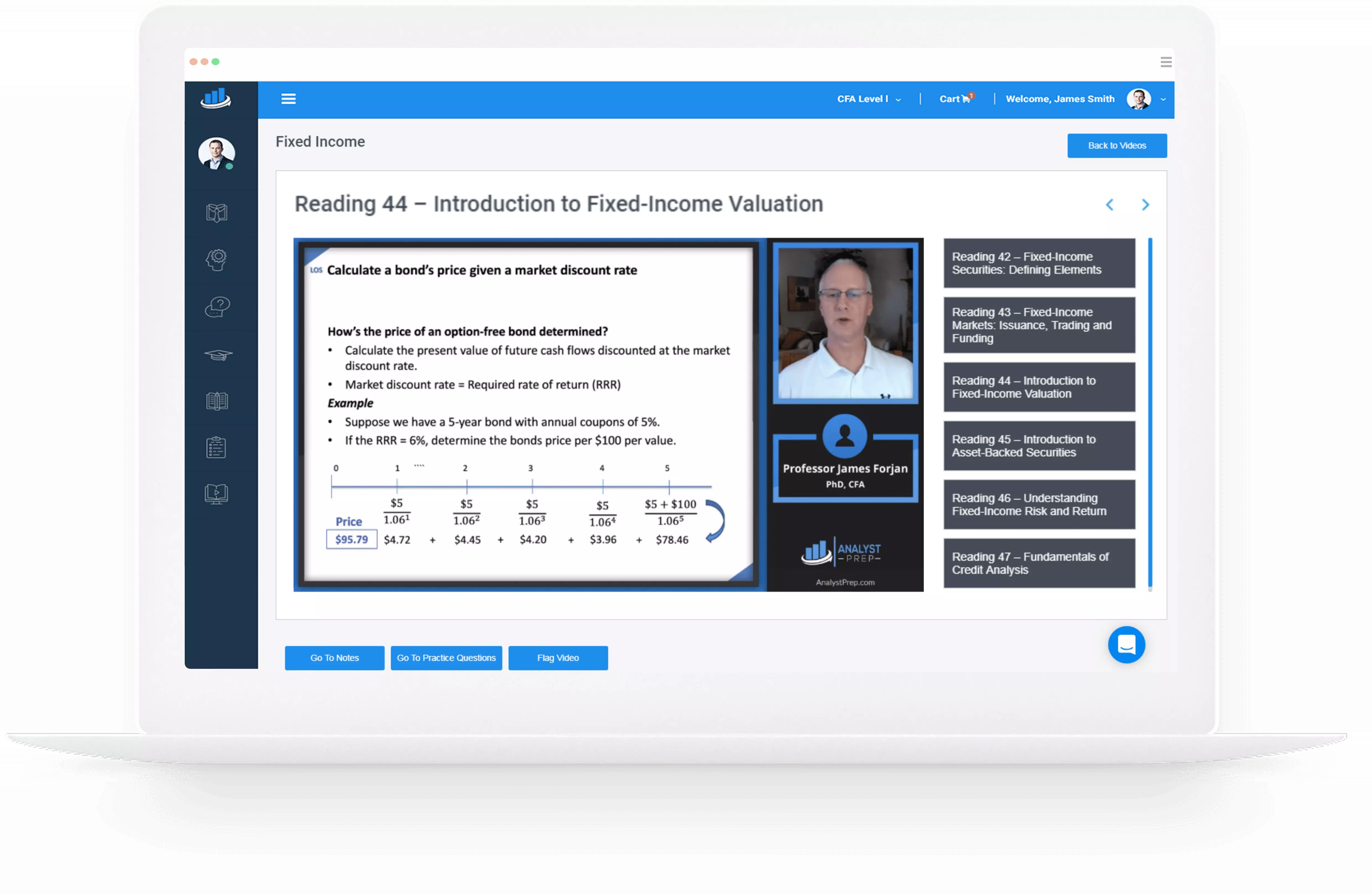
The Standard Normal Distribution: Calculation and Interpretation of Probability
The standard normal distribution refers to a normal distribution that has been standardized such that it has a mean of 0 and a standard deviation of 1. The shorthand notation used is:
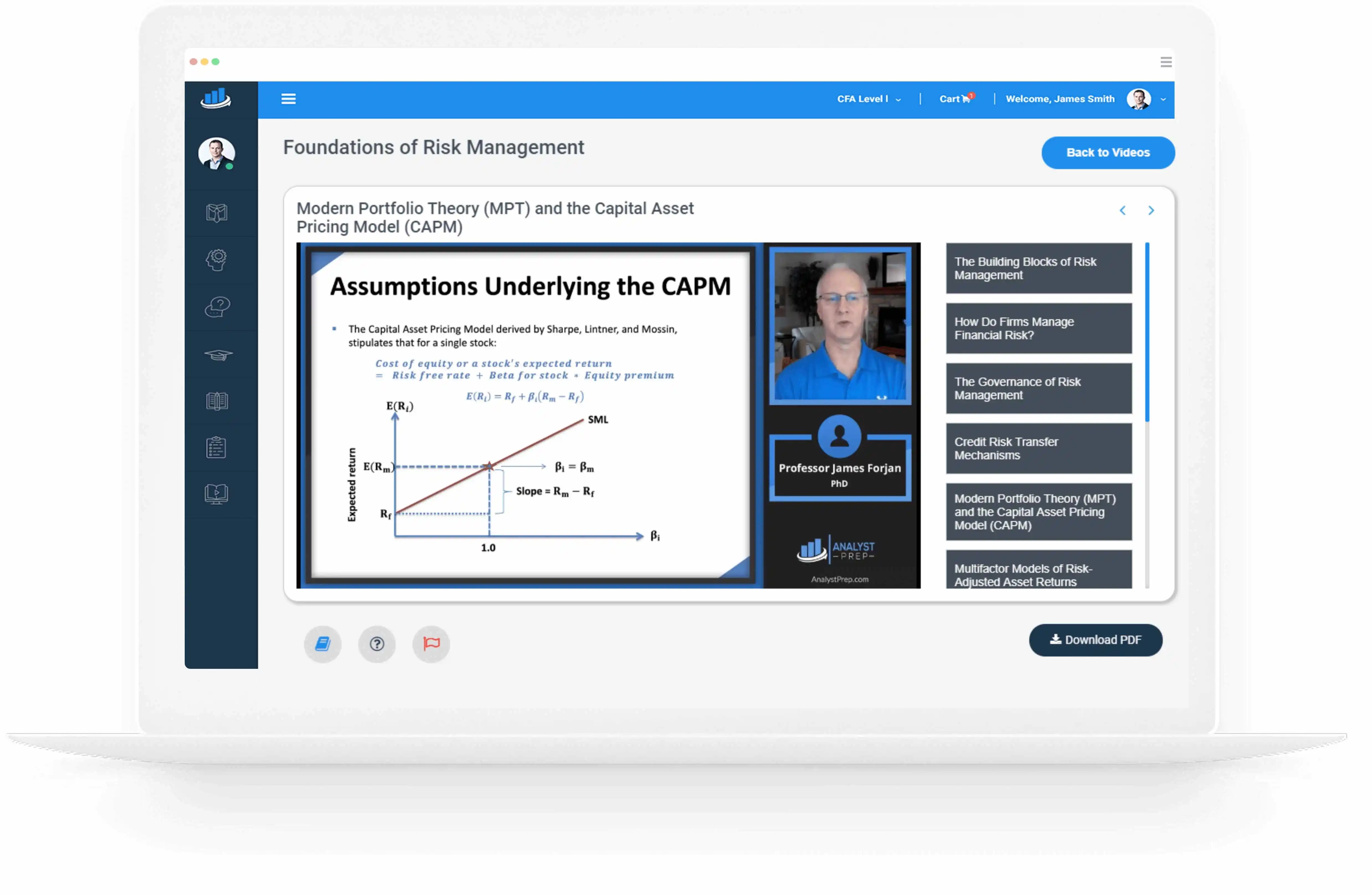
Shortfall Risk, Safety-first Ratio and Selection of an Optimal Portfolio Using Roy’s Safety-first Criterion
Shortfall Risk Shortfall risk refers to the probability that a portfolio will not exceed the minimum (benchmark) return that has been set by an investor. In other words, it is the risk that a portfolio will fall short of the…
The Lognormal Distribution vs. the Normal Distribution
A variable X is said to have a lognormal distribution if Y = ln(X) is normally distributed, where “ln” denotes the natural logarithm. In other words, when the logarithms of values form a normal distribution, we say that the original…
Continuous Compounding
Continuous compounding applies either when the frequency with which we calculate interest is infinitely large or the time interval is infinitely small. Put quite simply, under continuous compounding, time is viewed as continuous. This differs from discrete compounding where we…
Monte Carlo Simulations
Monte Carlo simulations involve the creation of a computer-based model into which the variabilities and interrelationships between random variables are entered. A spread of results is obtained when the model is run many times – hundreds or thousands of times….
Monte Carlo Simulation vs. Historical Simulation
Monte Carlo simulation and historical simulation are both methods that can be used to determine the riskiness of a financial project. However, each method uses different assumptions and techniques to develop the probability distribution of possible outcomes.
CFA Level 1 Study Notes – Financial Statement and Analysis
Study Session 6 Reading 15 – Introduction to Financial Statement Analysis –LOS 15a: describe the roles of financial reporting and financial statement analysis –LOS 15b: describe the roles of the statement of financial position, statement of comprehensive income, statement of…