Continuous Uniform Distribution

The continuous uniform distribution is such that the random variable X takes values between α (lower limit) and β (upper limit). In the field of statistics, α and β are known as the parameters of the continuous uniform distribution. We cannot have an outcome of either less than α or greater than β.

The probability density function for this type of distribution is:

$$ { f }_{ x }\left( x \right) =\frac { 1 }{ \beta -\alpha } \quad \quad \alpha < x < \beta $$

\(X \sim U (\alpha, \beta)\) is the most commonly used shorthand notation read as “the random variable x has a continuous uniform distribution with parameters α and β.”

The total probability (1) is spread uniformly between the two limits. Intervals of the same length have the same probability.

Properties of the Continuous Uniform Distribution

1. For all \(\alpha \le x_1 < x_2 \le \beta\)
2. \(P(X < \alpha) = P(X > \beta = 0)\)
3. \(P(x_1 \le X \le x_2) =\cfrac {(x_2 – x_1)}{(\beta – \alpha)}\)

Moments

$$ \text{Mean} =\cfrac {(\alpha + \beta)}{2} $$

$$ \text{Variance} =\cfrac {(\beta – \alpha)^2}{12} $$

Example: Probability Density Function

You have been given that \(Y \sim U(100,300)\). Calculate \(P(Y > 174)\) and \(P(100 < Y < 226\)

The probability density function is given by:

$$ f_x(x) =\cfrac {1}{(300 – 100)} =\cfrac {1}{200} $$

Therefore, each “unit interval” has a probability of \(\frac {1}{200}\).

Which means that \(P(Y > 174) =\cfrac {(300 – 174)}{200} = \cfrac {126}{200} = 0.63\)

Similarly, \(P(100 < Y < 226) = 0.63\) because the interval has the same length as above (126) hence the same probability.

The cumulative distribution function of the continuous uniform distribution looks like this:

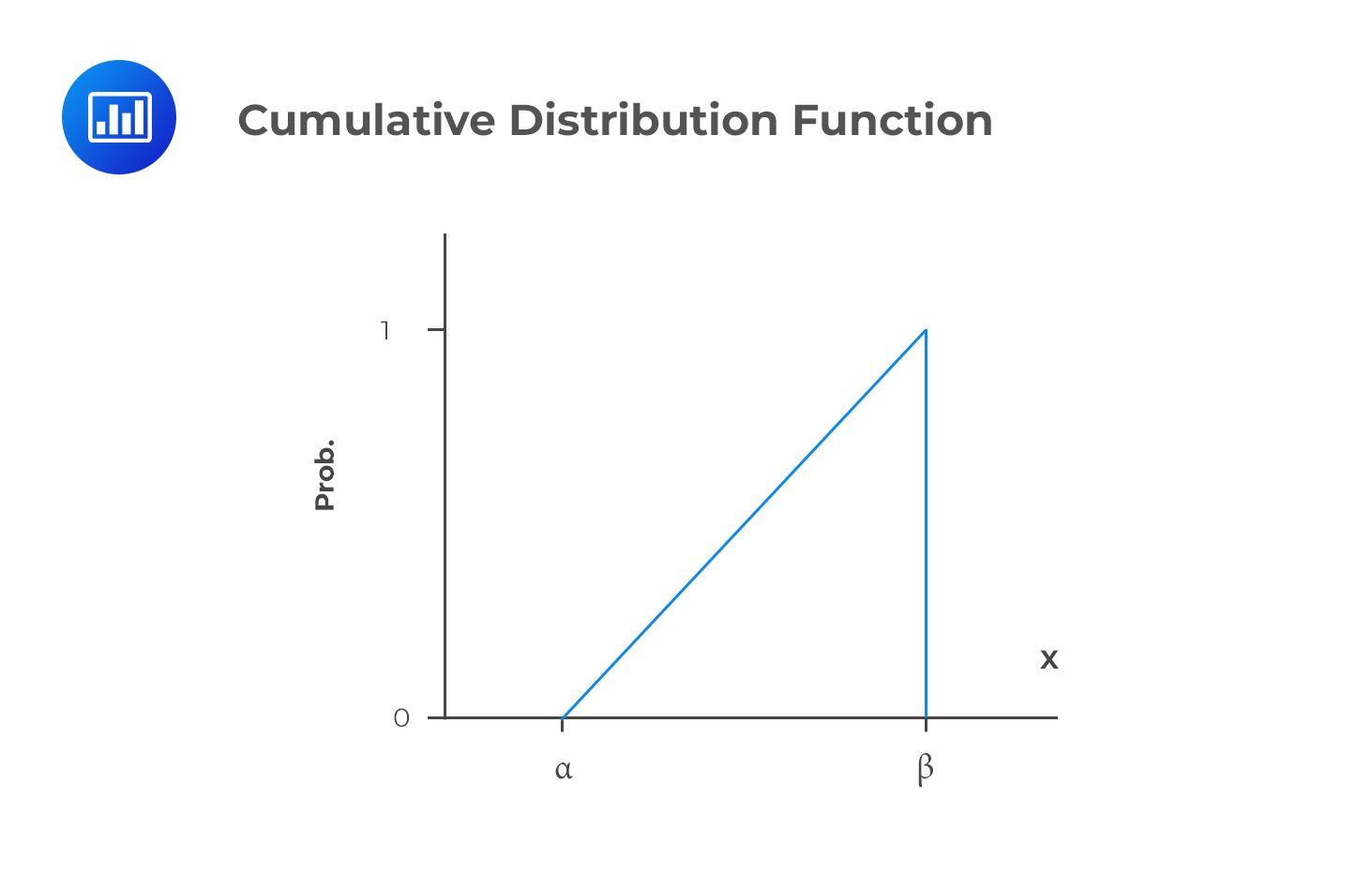
The CDF is linear over the variable’s range.

Question

A random variable X is uniformly distributed between 32 and 42. What is the probability that X will be between 32 and 40?

1. 8%
2. 10%
3. 80%

Solution

The correct answer is C.

First, you should determine the pdf:

$$ \begin{align*} f_x(x) & =\cfrac {1}{(42 – 32)} \\ &=\cfrac {1}{10} \\ \end{align*} $$

Therefore,

$$ P(32 < Y < 40) =\cfrac {(40 – 32)}{10} = 0.8 \text{ or } 80\%. $$