The Standard Normal Distribution: Calculation and Interpretation of Probability

The standard normal distribution refers to a normal distribution that has been standardized such that it has a mean of 0 and a standard deviation of 1. The shorthand notation used is:

$$ N \sim (0, 1) $$

In the context of statistics and mathematics, standardization is the process of converting an observed value for a random variable into a z-value where:

$$ \begin{align*} Z & = \cfrac {(\text{observed value} – \text{population mean})} {\text{standard deviation}} \\ & =\cfrac {(x – \mu)}{\sigma} \\ \end{align*} $$

The z-value, also referred to as the z-score in some books, represents the number of standard deviations a given observed value is from the population mean.

Example: Standard Normal Distribution

The returns on ABC stock are normally distributed where the mean is $0.60 with a standard deviation of $0.20. Calculate the z-scores for a return of $0.10.

Solution:

If the return is $0.10, then x = 0.1 (this is our observed value)

Therefore,

$$ \begin{align*} z & =\cfrac {(x – \mu)}{\sigma} \\ & =\cfrac {(0.1 – 0.6)}{0.2} \\ & = -2.5 \quad (\text{The return of }$0.1 \text{ is two and a half standard deviations below the mean}.) \end{align*} $$

We could get the z-score for any other observed value following a similar approach. For instance, the z-score for a return of $1 will be:

$$ \begin{align*} Z & =\cfrac {(1 – 0.6)}{0.2} \\ & = 2 \quad (\text{The return of } $1 \text{ is two standard deviations above the mean}) \\ \end{align*} $$

Calculating Probabilities Using z-values under the Standard Normal Distribution

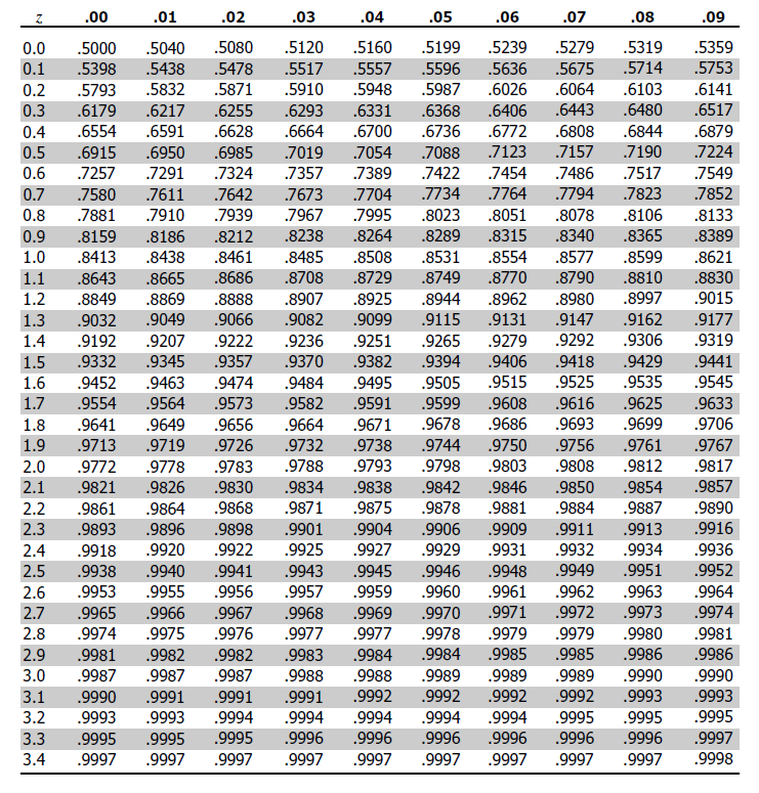
Using the standard normal distribution table, we can confirm that a normally distributed random variable Z, with mean equal to 0 and variance equal to 1, is less than or equal to z, i.e., P(Z ≤ z).

However, the table does this only when we have positive values of z. Simply put, if an examiner asks you to find the probability behind a given positive z-value, you’d have to look it up directly on the table.

P(Z ≤ z) = θ(z) when z is positive

Example: Using the z-score Table

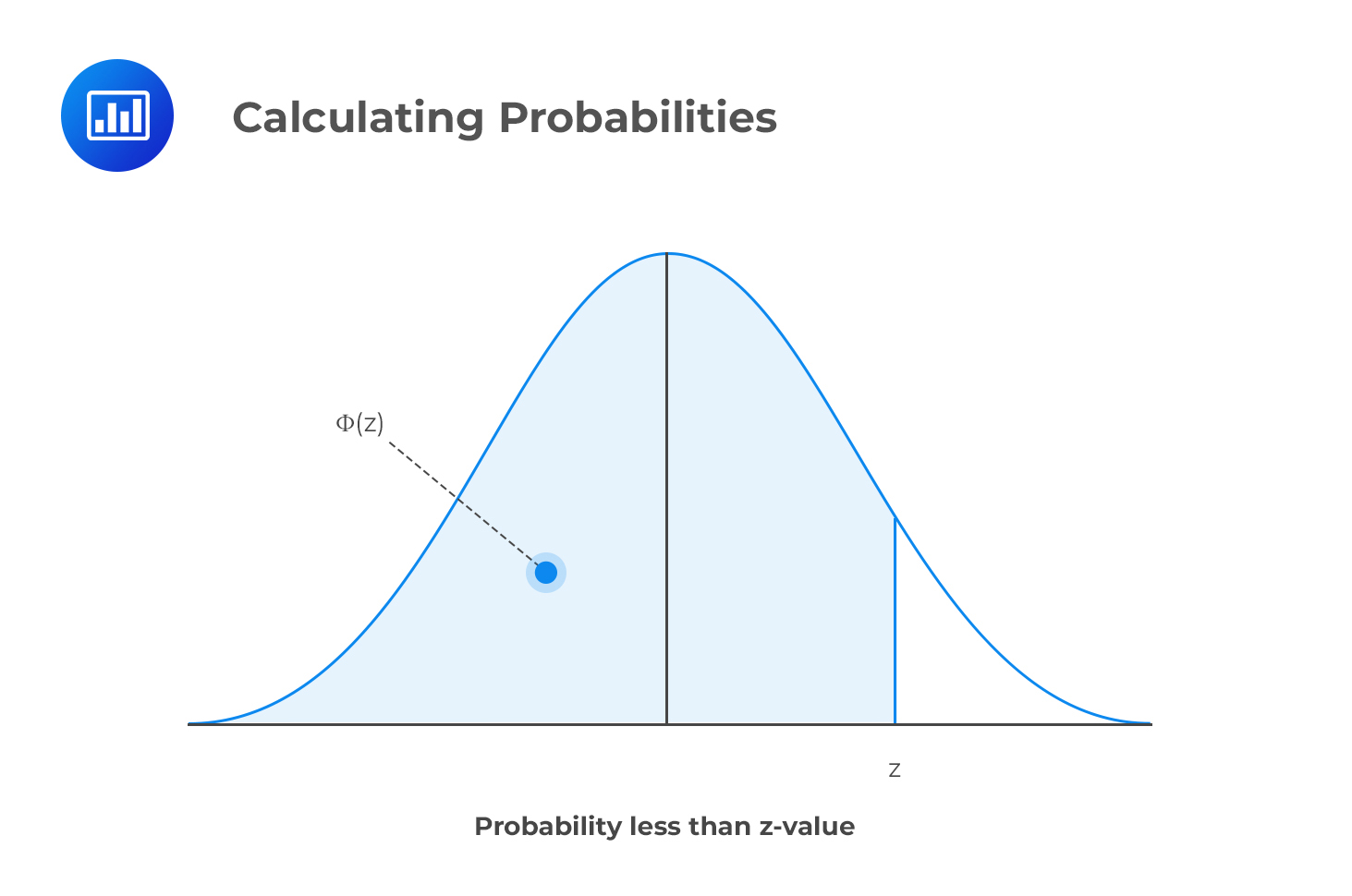
Using the data from our first example, calculate the probability that the return is less than $1.

Solution

First, you would be required to calculate the z-value (2 in this case).

P(Z ≤ 2) can be read off directly from the table.

You just move down and locate the z-value that lies to the right of “2,” i.e., 0.9772.

Negative z-values

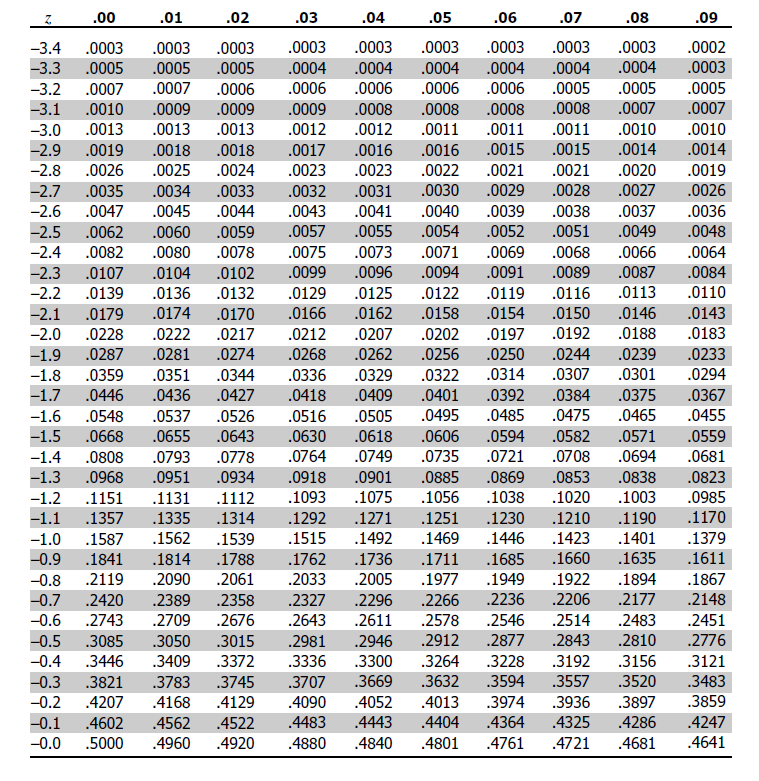
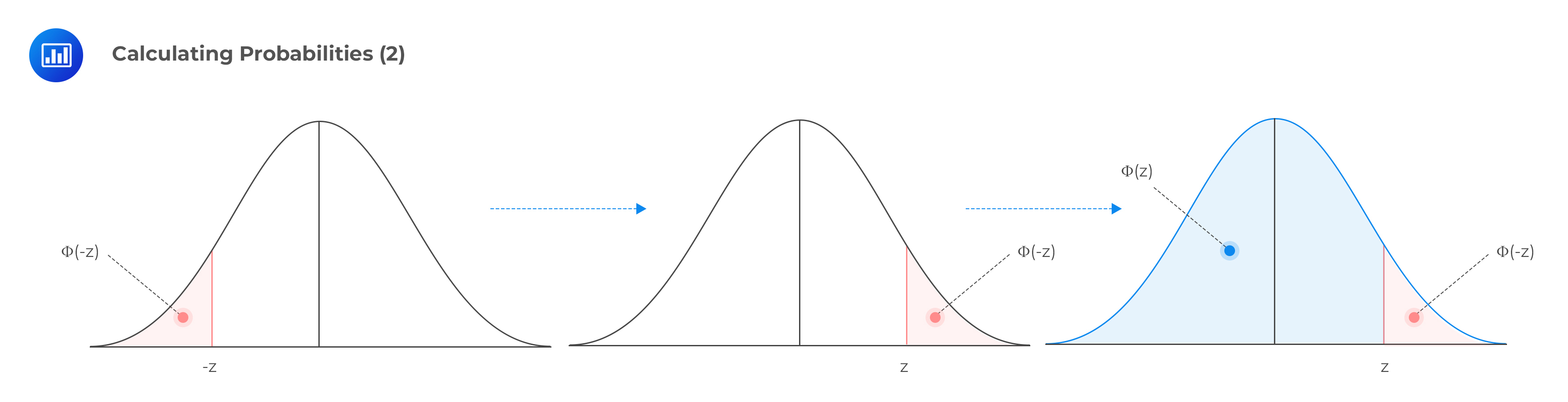
If we have a negative z-value and do not have access to the negative values from the table (as shown below), we can still calculate the corresponding probability by noting that:

$$ P(Z  \le -z) = 1 – P(Z \le z) \text{ or} $$

$$ \theta(–z) = 1 – \theta(z) $$

This relationship is true when we consider the following facts:

1. The total area (probability) under the standard normal distribution is 1.
2. The standardized normal distribution is symmetrical about the mean.

Question

Calculate P(Z  ≤ -2.5)

A. 0.9938

B. 0.0062

C. 0.06

Solution

The correct answer is B.

$$ \begin{align*} P(Z  \le -2.5) & = 1 – P(Z  \le 2.5) \\ & = 1 – 0.9938 \\ & = 0.0062 \\ \end{align*} $$