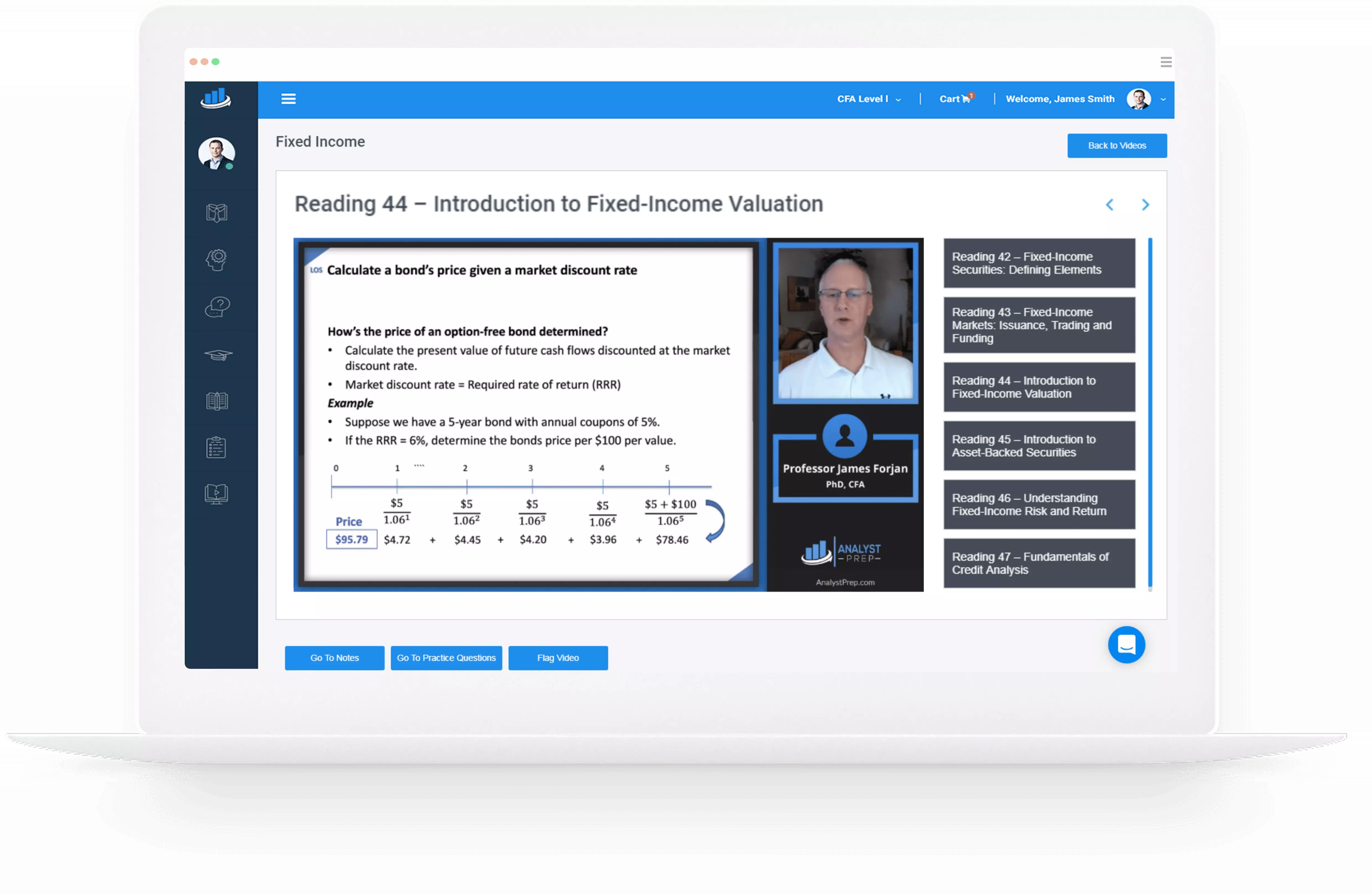
The Central Limit Theorem
The central limit theorem asserts that “given a population described by any probability distribution having mean \(\mu\) and finite variance \(\sigma^2\), the sampling distribution of the sample mean \(\bar{X}\) computed from random samples of size \(n\) from this population will…
Probability Sampling Methods
Sampling is the systematic process of selecting a subset or sample from a larger population. Sampling is essential because it is costly and time-consuming to analyze the whole population. Sampling methods can be broadly categorized into probability sampling and non-probability…
Bootstrap Resampling
Resampling Resampling means repeatedly drawing samples from the original observed sample to make statistical inferences about population parameters. There are two common methods: Bootstrap and jackknife. Here, we’ll focus on the Bootstrap method. Bootstrap Resampling Bootstrap resampling relies on computer…
Monte-Carlo Simulation
Monte Carlo simulations are about producing many random variables based on specific probability distributions. This helps in estimating the probability of various results. We will give an example to illustrate Monte Carlo Simulation implementation. Steps Involved in Project Appraisal Imagine…
Lognormal Distribution and Continuous Compounding
A random variable \(Y\) is lognormally distributed if its natural logarithm, In \(Y\), is normally distributed. The opposite is true. If ln \(Y\) is normally distributed, then \(Y\) is lognormally distributed. The lognormal distribution is positively skewed, meaning it’s skewed…
Bayes' Formula
Investors make investment decisions based on their experience and expertise. Their decisions may change in the wake of new knowledge and observations. Bayes’ formula allows us to update our decisions as we receive new information. In other words, Bayes’ formula…
Probability Trees
A tree diagram is a visual representation of all possible future outcomes and the associated probabilities of a random variable. Tree diagrams are handy when we have several possible outcomes. They facilitate the recording of all the possibilities in a…
Expected Values, Variances, and Standard Deviations
Expected Value Expected value is an essential quantitative concept investors use to estimate investment returns and analyze any factor that may impact their financial position. Mathematically, the expected value is the probability-weighted average of the possible outcomes of the random…
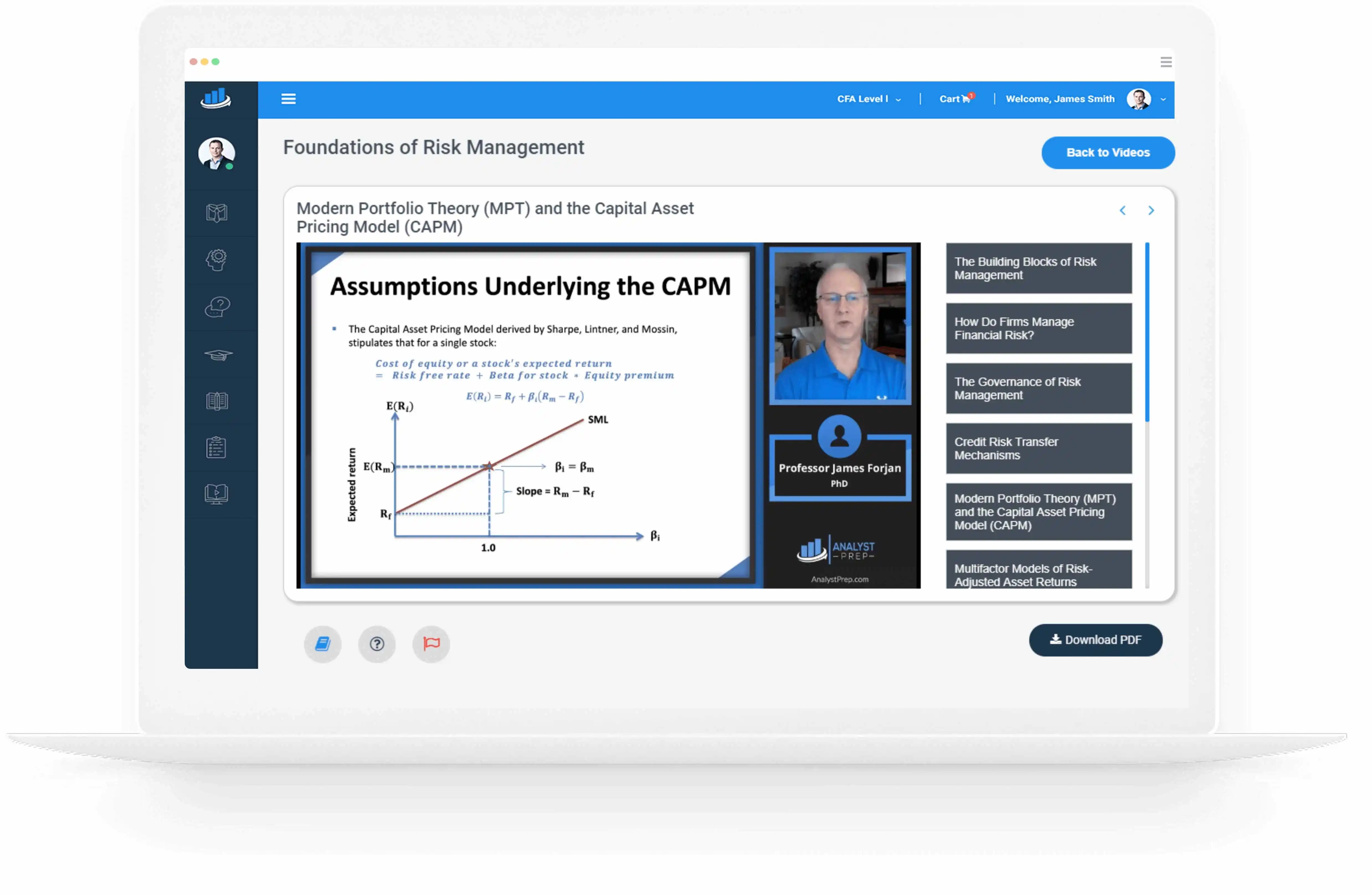
Portfolio Risk Measures
Modern Portfolio Theory (MPT) evaluates investment options based on mean return and return variance. This approach is applicable when investors are risk-averse, meaning they seek to maximize their expected satisfaction or utility from their investments. Mean-return analysis holds under two…
Covariance, Correlation, and Joint Probability
Historical covariance or other techniques, such as market model regression with historical return data, can help us forecast return covariance and correlation. We use the joint probability function of the random variables for this estimation. The probability that values of…