Sample Moments

After completing this reading, you should be able to:

• Estimate the mean, variance, and standard deviation using sample data.
• Explain the difference between a population moment and a sample moment.
• Distinguish between an estimator and an estimate.
• Describe the bias of an estimator and explain what the bias measures.
• Explain what is meant by the statement that the mean estimator is BLUE.
• Describe the consistency of an estimator and explain the usefulness of this concept.
• Explain how the Law of Large Numbers (LLN) and Central Limit Theorem (CLT) apply to the sample mean.
• Estimate and interpret the skewness and kurtosis of a random variable.
• Use sample data to estimate quantiles, including the median.
• Estimate the mean of two random variables and apply the CLT.
• Estimate the covariance and correlation between two random variables.
• Explain how coskewness and cokurtosis are related to skewness and kurtosis.

Sample Moments

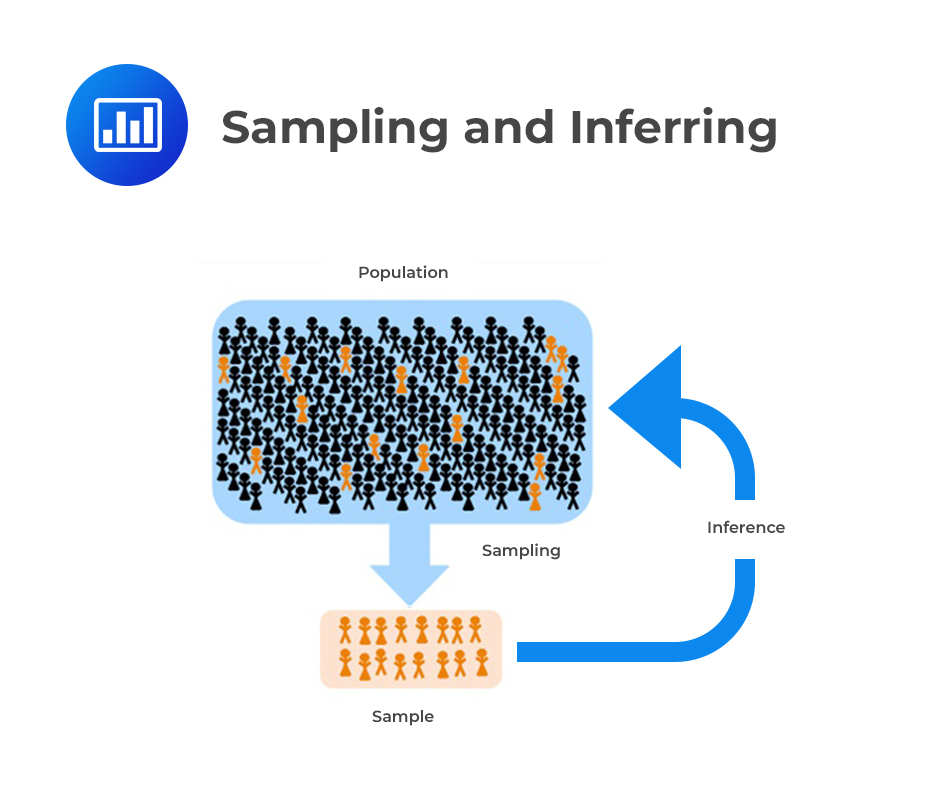
Recall that moments are defined as the expected values that briefly describe the features of a distribution. Sample moments are those that are utilized to approximate the unknown population moments. Sample moments are calculated from the sample data.

Such moments include mean, variance, skewness, and kurtosis. We shall discuss each moment in detail.

Estimation of the Mean

The population mean, denoted by \(\mu\) is estimated from the sample mean \((\bar {\text X} )\). The estimated mean is denoted by \(\hat \mu\) and defined by:

$$ \hat {\mu} =\bar {\text X} =\frac {1}{n} \sum_{i=1}^n \text X_\text i  $$

Where \(\text X_\text i\) is a random variable assumed to be independent and identically distributed so  \(\text E(\text X_\text i)=\mu\) and n is the number of observations.

Note that the mean estimator is a function of random variables, and thus it is a random variable. Consequently, we can examine its properties as a random variable (its mean and variance)

For instance, the expectation of the mean estimator \(\hat \mu\) is the population mean \( \mu\). This can be seen as follows:

$$ \text E(\hat \mu)=\text E(\bar {\text X})=\text E \left[ \frac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i \right]=\frac {1}{\text n} \sum_{\text i=1}^\text n \text E(\text X_\text i )=\frac {1}{\text n} \sum_{\text i=1}^\text n \mu=\frac {1}{\text n}×\text n \mu=\mu  $$

The above result is true since we have assumed that \(\text X_i\)’s are iid. The mean estimator is an unbiased estimator of the population mean.

The bias of an estimate is defined as:

$$ \text{Bias}(\hat \theta )=\text E(\hat \theta )-\theta $$

Where \(\hat \theta \) is the true estimator of the population value θ. So, in the case of the population mean:

$$ \text{Bias}(\hat \mu )=\text E(\hat \mu)-\mu =\mu – \mu =0 $$

Since the value of the mean estimator is 0, it is an unbiased estimator of the population mean.

Using conventional features of a random variable, the variance of the mean estimator is calculated as:

$$ \text{Var}(\hat \mu)=\text{Var} \left(\frac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i \right)=\frac {1}{\text n^2}  \left[\sum_{\text i=1}^\text n \text{Var}(\text X_\text i )+\text{Covariances} \right] $$

But we are assuming that \(\text X_\text i\)’s are iid, and thus they are uncorrelated, implying that their covariance is equal to 0. Consequently, taking \(\text{Var}(\text X_\text i )=\sigma^2\), the above formula changes to:

$$ \text{Var}(\hat \mu)=\text{Var} \left(\frac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i \right)=\frac {1}{\text n^2}  \left[\sum_{\text i=1}^\text n \text {Var}(\text X_\text i)\right]=\frac {1}{\text n^2}  \left[ \sum_{\text i=1}^\text n \sigma^2 \right]=\frac {1}{\text n}^2 ×\text n \sigma^2=\frac {\sigma^2}{\text  n} $$

Thus

$$ \text{Var}(\hat \mu)=\frac {\sigma^2}{\text  n} $$

Looking at the last formula, the variance of the mean estimator depends on the data variance \((\sigma^2)\) and the sample mean n. Consequently, the variance of the mean estimator decreases as the number of the observations (sample size) is increased. This implies that the larger the sample size, the closer the estimated mean to the population mean.

Example: Calculating the Sample Mean

An experiment was done to find out the number of hours that candidates spend preparing for the FRM part 1 exam. It was discovered that for a sample of 10 students, the following times were spent:

$$ 318, 304, 317, 305, 309, 307, 316, 309, 315, 327 $$

What is the sample mean?

Solution

We know that:

$$ \begin{align*} \bar {\text X} & =\hat \mu=\frac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i \\ \Rightarrow \bar {\text X} & =\frac {318+304+ 317+ 305+ 309+ 307+316+ 309+ 315+ 327}{10} \\ & =312.7 \\ \end{align*} $$

Desirable Properties of the Sample Mean Estimator

• The mean estimator is averagely equal to the population mean.
• As the sample size (the number of the observation) increases, the sample mean tends to the population mean.
• The sample mean can be assumed to be distributed normally (normal distribution)

Estimation of Variance and Standard Deviation

The sample estimator of variance is defined as:

$$ \hat \sigma^2=\frac {1}{\text n} \sum_{\text i=1}^\text n \left(\text X_\text i-\hat \mu \right)^2 $$

Note that we are still assuming that \(X_i\)’s are iid. As compared to the mean estimator, the sample estimator of variance is biased. It can be proved that: $$ \text{Bias}(\hat \sigma^2 )=\text E(\hat \sigma^2 )-\sigma^2=\frac {\text n-1}{\text n} \sigma^2-\sigma^2=\frac {\sigma^2}{\text n} $$

This implies that the bias decreases as the number of observations are increased. Intuitively, the source of the bias is the variance of the mean estimator \((\frac {\sigma^2}{\text n})\). Since the bias is known, we construct an unbiased estimator of variance as:

$$ \text s^2=\frac {\text n}{\text n-1} {\hat \sigma}^2=\frac {\text n}{\text n-1}×\frac {1}{\text n} \sum_{\text i=1}^\text n (\text X_\text i-{\hat \mu})^2 =\frac {1}{\text n-1} \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu)^2 $$

It can be shown that \(\text E(\text s^2 )=\sigma^2\) and thus \(\text s^2 \) is an unbiased variance estimator. Maintaining this line of thought, it might seem \(\text s^2\)  is a better estimator of variance than \(\hat \sigma^2\) but this is not necessarily true since the variance of \(\hat \sigma^2\) is less than that of  \(\text s^2\). However, financial analysis involves large data sets, and thus either of these values can be used. However, when the number of observations is more than 30 \((\text n \ge 30)\), \(\hat \sigma^2\) is preferred conventionally.

The sample standard deviation is the square root of the sample variance. That is:

$$ \hat \sigma=\sqrt{\hat \sigma^2} $$

or

$$ \text s=\sqrt{\text s^2} $$

Note that the square root is a nonlinear function, and thus, the standard deviation estimators are biased but diminish as the sample size increases.

Example: Calculating the Sample Variance Estimator (Unbiased)

Using the example as in calculating the sample mean, what is the sample variance?

Solution

The sample estimator of variance is given by:

$$ \text s^2=\frac {1}{\text n-1} \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu)^2  $$

To make it easier, we will calculate we make the following table:

$$ \begin{array}{c|c} \bf{\text X_\text i} &       \bf{(\text X_\text i-\hat \mu)^2} \\ \hline {318} & {(318-312.7)^2=28.09} \\ \hline {304} &                 {75.69} \\ \hline {317} & {18.49} \\ \hline {305} & {59.29} \\ \hline {309} & {13.69} \\ \hline {307} & {32.49} \\ \hline {316} & {10.89} \\ \hline {309} & {13.69} \\ \hline {315} & {5.29} \\ \hline {327} & {204.49} \\ \hline \textbf{Total} & \bf{462.1} \\ \end{array} $$

So, the variance is given to be:

$$ \text s^2=\frac {1}{\text n-1} \sum_{\text i=1}^\text n \left(\text X_\text i-\hat \mu \right)^2 =\frac {462.1}{10-1}=51.34$$

Reasons, why Mean and Standard Deviations are Used

1. The mean and the variance are almost adequate to describe data.
2. They give a clue on the range of the values that can be observed.
3. The units of the mean and the standard deviation are the same as those of the data, and thus they can be easily compared.

Skewness

As we saw in chapter two, the skewness is a cubed standardized central moment given by:

$$ \text{skew}(\text X)=\cfrac {\text E(\left[\text X-\text E(\text X)\right]^3 }{\sigma^3} =\text E \left[\left(\frac{X-\mu}{\sigma} \right)^3 \right] $$

Note that \(\frac {X-\mu}{\sigma}\) is a standardized X with a mean of 0 and variance of 1.

This can also be written as:

$$ \text{skew}(\text X)=\cfrac { \text E([\text X-\text E(\text X)]^3 }{ \text E \left [(\text X-\text E(\text X))^2 \right ]^{\frac {3}{2}}} =\frac {\mu_3}{\sigma^3} $$

Where \(\mu_3\) is the third central moment, and \(\sigma\) is the standard deviation

The skewness measures the asymmetry of the distribution (since the third power depends on the sign of the difference). When the value of the asymmetry is negative, there is a high probability of observing the large magnitude of negative value than positive values (tail is on the left side of the distribution). Conversely, if the skewness is positive, there is a high probability of observing the large magnitude of positive values than negative values (tail is on the right side of the distribution).

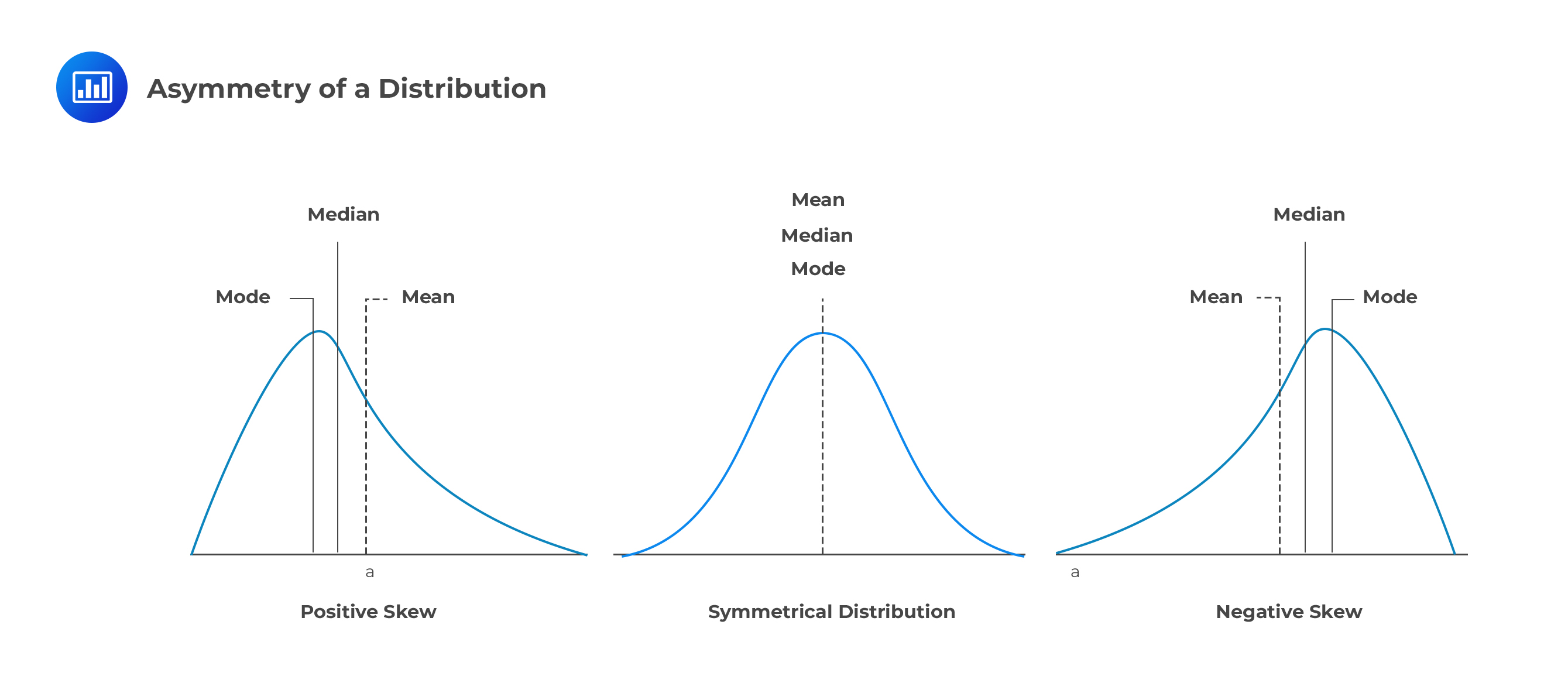The estimators of the skewness utilize the principle of expectation and is denoted by:

$$ \frac {\hat \mu^3}{\hat \sigma^3} $$

We can estimate \(\hat \mu^3\) as:

$$ \hat \mu^3=\frac {1}{n} \sum_{\text i=1}^\text n (\text x_\text i-{\hat \mu})^3 $$

Example: Calculating the Skewness

The following are the data on the financial analysis of a sales company’s income over the last 100 months:

\( \text n=100, \sum_{\text i=1}^\text n ( \text x_\text i-\hat \mu)^2 =674,759.90\).  and \(\sum_{\text i=1}^\text n (\text x_\text i-\hat \mu)^3=-12,456.784 \)

Calculate that Skewness.

Solution

The skewness is given by:

$$ \cfrac {\hat \mu^3}{\hat\sigma^3} =\cfrac {  \frac{1}{n} \sum_{\text i=1}^\text n (\text x_{\text i}-\hat \mu)^3 }{\left[ \frac {1}{\text n} \sum_{\text i=1}^\text n (\text x_{\text i}-{\hat \mu})^2 \right]^{\frac {3}{2}}} =\cfrac { \frac {1}{100} \left(-12,456.784 \right) }{ \left[ \frac {1}{100} ×674,759.90 \right]^{\frac {3}{2}}} =-0.000225 $$

Kurtosis

The Kurtosis is defined as the fourth standardized moment given by:

$$ \text{Kurt}(\text X)=\cfrac {\text E([\text X-\text E(\text X)])^4 }{\sigma^4} =\text E\left[ \left( \frac{\text X-\mu}{\sigma} \right)^4 \right] $$

The above can be written as:

$$ \text{Kurt}(\text X)=\cfrac {\text E([\text X-\text E(\text X)]^4 }{\text E[(\text X-\text E(\text X))^2]^2} =\cfrac {\mu_4}{\sigma^4} $$

The description of kurtosis is analogous to that of the Skewness, only that the fourth power of the Kurtosis implies that it measures the absolute deviation of random variables. The reference value of a normally distributed random variable is 3.  A random variable with Kurtosis exceeding 3 is termed to be heavily or fat-tailed.

The estimators of the skewness utilize the principle of expectation and is denoted by:

$$ \frac{\hat \mu_4}{\hat \sigma^4} $$

We can estimate \({\hat \mu_4}\) (fourth central moment) as:

$$ \hat \mu_4=\frac{1}{n} \sum_{\text i=1}^\text n (\text x_\text i-\hat \mu)^4 $$

The BLUE Mean Estimator

We say that the mean estimator is the Best Linear Unbiased Estimator (BLUE) of the population mean when the data used are iid. That is,

1. The variance of the mean has the lowest variance of any Linear Unbiased Estimator (LUE).
2. It is the unbiased estimator of the population mean (as shown earlier)
3. It is a linear function of the data used.

The linear estimators are a function of the mean and can be defined as:

$$ \hat \mu=\sum_{\text i=1}^\text n \omega_\text i \text X_\text i $$

Where \(\omega_\text i\) is independent of \(\text X_\text i\) . In the case of the sample mean estimator, \(\omega_\text i=\frac {1}{n}\). Recall that we had shown the unbiases of the sample mean estimator.

BLUE puts an estimator as the best by having the smallest variance among all linear and unbiased estimators. However, there are other superior estimators, such as Maximum Likelihood Estimators (MLE).

The Behavior of Mean in Large Sample Sizes

Recall that the mean estimator is unbiased, and its variance takes a simple form. Moreover, if the data used are iid and normally distributed, then the estimator is also normally distributed. However, it poses a great difficulty in defining the exact distribution of the mean in a finite number of observations.

To overcome this, we use the behavior of the mean in large sample sizes (that is as \(\text n \rightarrow \infty\)) to approximate the distribution of the mean infinite sample sizes. We shall explain the behavior of the mean estimator using the Law of Large Numbers (LLN) and the Central Limit Theorem (CLT).

The Law of Large Numbers (LLN)

The law of large numbers (Kolmogorov Strong Law of Large Numbers) for iid states that if \(\text X_\text i\)’s is a sequence of random variables, with \(\text E(\text X_\text i )\equiv \mu \) then:

$$ \hat \mu_{\text n}=\frac {1}{\text n} \sum_{\text i=1}^{\text n} \text X_\text i^{ \underrightarrow { a.s }  }\mu $$

Put in words, the sample mean estimator \(\hat \mu_{\text n}\) converges almost surely \((^{ \underrightarrow { a.s }  })\) to population mean \((\mu)\).

An estimator is said to be consistent if LLN applies to it. Consistency requires that an estimator is:

1. Unbiased and that the bias should decrease as n  increases.
2. The variance decreases as the number of observations n increases. That is:\(\text{Var}(\hat \mu_{\text n} )\rightarrow 0\).

Moreover, under LLN, the sample variance is consistent. That is, LLN implies that  \({\hat \sigma^2}^{ \underrightarrow { a.s }  } \sigma^2\)

However, consistency is not easy to study because it tends to 0 as \(n \rightarrow \infty\).

The Central Limit Theorem (CLT)

The Central Limit Theorem (CLT) states that if \(\text X_1,\text X_2,…,\text X_\text n\) is a sequence of iid random variables with a finite mean \(\mu\) and a finite non-zero variance \(\sigma^2\), then the distribution of \(\frac {\hat \mu -\mu}{\frac {\sigma}{\sqrt n}}\) tends to a standard normal distribution as \(\text n\rightarrow \infty\).

Put simply,

$$ \frac {\hat \mu -\mu}{\frac {\sigma}{\sqrt n}}\rightarrow  \text N(0,1) $$

Note that \(\hat \mu = \bar X=\text{Sample Mean}\)

Note that CLT extends LLN and provides a way of approximating the distribution of the sample mean estimator. CLT seems to be appropriate since it does not require the distribution of random variables used.

Since CLT is asymptotic, we can also use the unstandardized forms so that:

$$ \hat \mu \sim \text N \left(\mu,\frac {\sigma^2}{\text n} \right) $$

Note that we can go back to standard normal variable Z as:

$$ \text Z=\frac {\hat \mu-\mu}{\frac {\sigma}{\sqrt n}} $$

Which is actually the result we have initially.

The main question is, how large is n?

The value of n solely depends on the shape of the population (distribution of \(\text X_\text i\)’s), i.e., the skewness. However, CLT is appropriate when \(n \ge 30\)

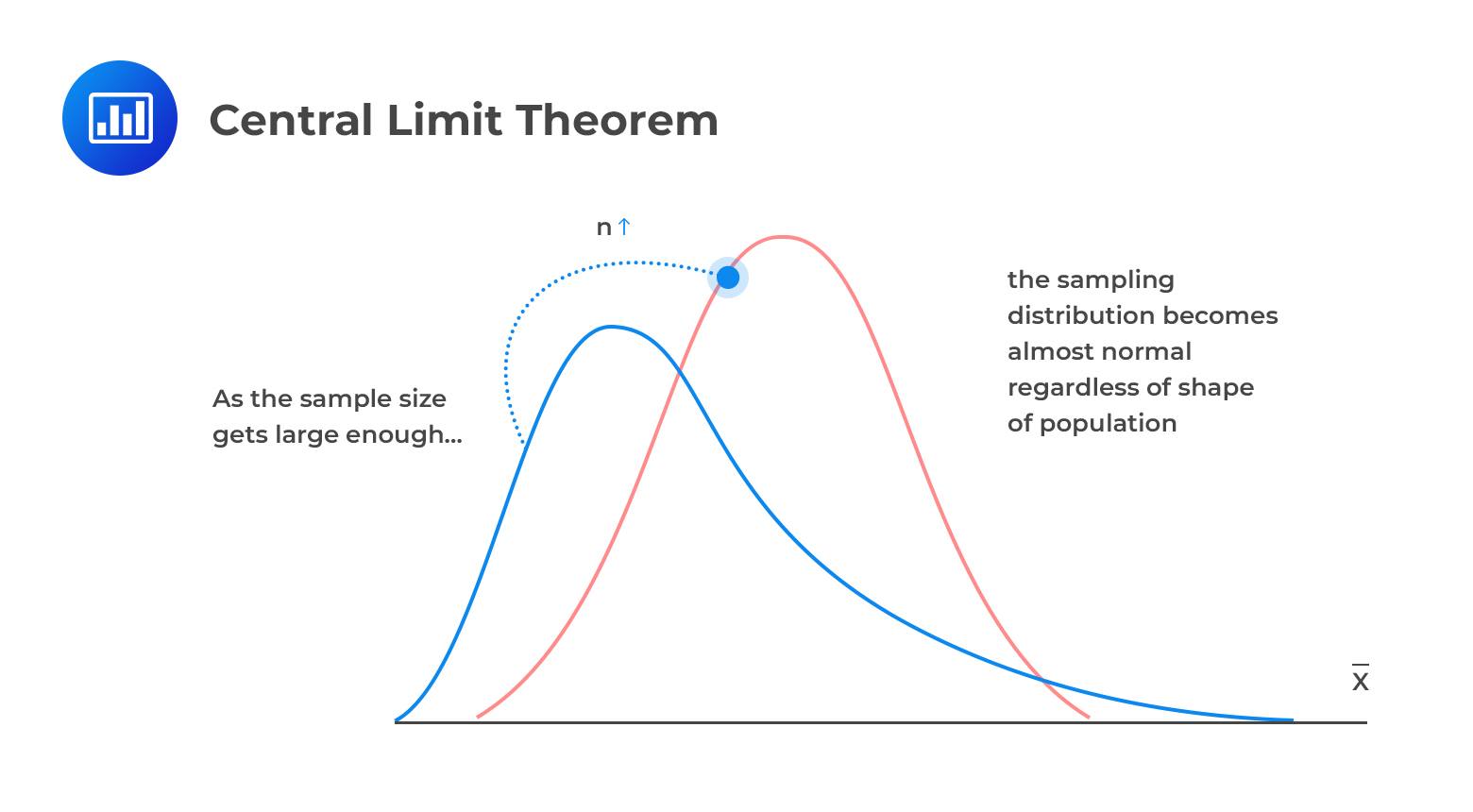Example: Applying CLT

A sales expert believes that the number of sales per day for a particular company has a mean of 40 and a standard deviation of 12. He surveyed for over 50 working days. What is the probability that the sample mean of sales for this company is less than 35?

Solution

Using the information given in the question,

\(\mu=40, \sigma=12\) and n=50

By central limit theorem,

$$ \hat \mu \sim \text N \left(\mu,\frac {\sigma^2}{n} \right) $$

We need

$$ \begin{align*} \text P(\hat \mu < 35) & =\text P \left[\text Z < \frac {35-40}{\frac {12}{\sqrt{50}}} \right]=\text P(\hat \mu < -2.946) \\ & =\text P(\hat \mu < -2.946)=1- \text P(\hat \mu < 2.946)=0.00161 \\ \end{align*} $$

Estimation of Median and Other Quantiles

Median

Median is a central tendency measure of distribution, also called the 50% quantile, which divides the distribution in half ( 50% of observations lie on either side of the median value).

The estimation of the mean involves arranging the data in ascending or descending order. If the number of the observations is odd, the median is \(\left( \frac {n+1}{2} \right)\)  the value in the list and thus the median is:

$$ \text {Med}(\text x)=x_{\frac {\text n}{2}+1} $$

If the number of the observations is even, the median is estimated by averaging the two consecutive central points. That is:

$$ \text{Med}(\text x)=\cfrac {1}{2} \left[ x_{\frac {\text n}{2}}+x_{\frac {\text n}{2}+1} \right] $$

Example: Calculating the Median

The ages of experienced financial analysts in a country are:

$$ 56,51,43,34,25,50. $$

What is the median age of the analysts?

Solution

We need to arrange the data in ascending order:

$$ 25,34,43,50,51,56 $$

The sample size is 6 (even), so the median is given by:

$$ \text{Med}(\text{Age})=\cfrac {1}{2} \left[ \text x_{\frac {6}{2}}+ \text x_{\frac {6}{2}+1} \right]=\cfrac {1}{2} \left(\text x_3+\text x_4 \right)=\cfrac {1}{2} \left( 43+50 \right)=46.5 $$

Properties of the Median

• It may not be an actual observation in the data set.
• It is not affected by extreme values because the median is a positional measure.
• It is used when the exact midpoint of the score distribution is desired, or when there are many outliers (extreme observations).

Other Quartiles

For other quantiles such as 25% and 75% quantiles, we estimate analogously as the median. For instance, a θ-quantile is determined using the nθ, which is a value in the sorted list. If nθ is not an integer, we will have to take the average below or above the value nθ.

So, in our example above, the 25% quantile (θ=0.25) is 6×0.25=1.5. This implies that we need to find the average value of the 1st and 2nd values:

$$ \hat {\text q}_{25}=\cfrac {1}{2} (25+34)=29.5 $$

The Interquartile Range

The interquartile range (IQR) is defined as the difference between the 75% and 25% quartiles. That is:

$$ \widehat {(\text{IQR})} =\hat {\text q}_{75}-\hat {\text q}_{25} $$

IQR is a measure of dispersion and thus can be used as an alternative to the standard deviation

If we use the example above, the 75% quantile is 6×0.75=4.5. So, we need to average the 4^th and 5^th values:

$$ \hat {\text q}_{75}=\cfrac {1}{2} (50+51)=50.5 $$

So that the IQR is:

$$ \widehat {(\text{IQR})} =50.5-29.5=21 $$

Desirable Properties of Quantiles

1. The units of the quantiles are the same as those of the data used hence they are easy to interpret.
2. They are robust to outliers of the data. The median and the IQR are unaffected by the outliers.

The Multivariate Moments

We can extend the definition of moments from the univariate to multivariate random variables. The mean is unaffected by this because it is just the combination of the means of the two univariate sample means.

However, if we extend the variance, we would need to estimate the covariance between each pair plus the variance of each data set used. Moreover, we can also define Kurtosis and Skewness analogously to univariate random variables.

Covariance

In covariance, we focus on the relationship between the deviations of some two variables rather than the difference from the mean of one variable.

Recall that the covariance of two variables X and Y is given by:

$$ \begin{align*} \text{Cov}(\text X, \text Y) & =\text E[( \text X-\text E[\text X])]\text E[(\text Y-\text E[\text Y])] \\ & =\text E[\text {XY}]-\text E[\text X]\text E[\text Y] \\ \end{align*} $$

The sample covariance estimator is analogous to this result. The sample covariance estimator is given by:

$$ \hat \sigma_\text{XY}=\cfrac {1}{\text n} \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu_\text X)(\text Y_\text i-\hat \mu_\text Y) $$

Where

\(\hat \mu_\text X\)-the sample mean of X

\(\hat \mu_\text Y\)- the sample mean of Y

The sample covariance estimator is biased towards zero, but we can remove the estimator by using n-1 instead of just n.

Correlation

Correlation measures the strength of the linear relationship between the two random variables, and it is always between -1 and 1. That is \(-1 < \text{Corr}(\text X_1,\text X_1 ) < 1\).

Correlation is a standardized form of the covariance. It is approximated by dividing the sample covariance by the product of the sample standard deviation estimator of each random variable. It is defined as:

$$ \rho_\text{XY}=\cfrac {\hat \sigma_\text{XY}}{\sqrt{\hat \sigma_\text X^2} \sqrt{\hat \sigma_\text Y^2 }}=\cfrac {\hat \sigma_\text{XY}}{\hat \sigma_\text X \hat \sigma_\text Y } $$

Sample Mean of Two Variables

We estimate the mean of two random variables the same way we estimate that of a single variable.  That is:

$$ \hat \mu_\text x=\cfrac {1}{\text n} \sum_{\text i=1}^\text n (\text x_\text i) $$

And

$$ \hat \mu_\text y=\frac {1}{\text n} \sum_{\text i=1}^\text n (\text y_\text i) $$

Assuming both of the random variables are iid, we can apply CLT in each estimator. However, if we consider the joint behavior (as a bivariate statistic), CLT stacks the two mean estimators into a 2×1 matrix:

$$ \hat \mu=\left[ \begin{matrix} { \hat { \mu  }  }_{ x } \\ { \hat { \mu  }  }_{ y } \end{matrix} \right]  $$

Which is normally distributed as long the random variable Z=[X, Y] is iid. The CLT on this vector depends on the covariance matrix:

$$ \begin{bmatrix} { \sigma  }_{ X }^{ 2 } & { \sigma  }_{ XY } \\ { \sigma  }_{ XY } & { \sigma  }_{ Y }^{ 2 } \end{bmatrix} $$

Note that in a covariance matrix, one diagonal displays the variance of random variable series, and the other is covariances between the pair of the random variables. So, the CLT for bivariate iid data is given by:

$$ \sqrt { n } \left[ \begin{matrix} { \hat { \mu  }  }_{ x }-{ \mu  }_{ x } \\ { \hat { \mu  }  }_{ y }-{ \mu  }_{ y } \end{matrix} \right] \rightarrow N\left( \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right] ,\begin{bmatrix} { \sigma  }_{ X }^{ 2 } & { \sigma  }_{ XY } \\ { \sigma  }_{ XY } & { \sigma  }_{ Y }^{ 2 } \end{bmatrix} \right) $$

If we scale the difference between the vector of means,  then the vector of means is normally distributed. That is:

$$ \left[ \begin{matrix} { \hat { \mu  }  }_{ x } \\ { \hat { \mu  }  }_{ y } \end{matrix} \right] \rightarrow N\left( \left[ \begin{matrix} { \mu  }_{ x } \\ { \mu  }_{ y } \end{matrix} \right] ,\begin{bmatrix} \frac { { \sigma  }_{ X }^{ 2 } }{ n }  & \frac { { \sigma  }_{ XY } }{ n }  \\ \frac { { \sigma  }_{ XY } }{ n }  & \frac { { \sigma  }_{ Y }^{ 2 } }{ n }  \end{bmatrix} \right)  $$

Example: Applying Bivariate CLT

The annualized estimates of the means, variances, covariance, and correlation for monthly return of stock trade (T) and the government’s bonds (G) for 350 months are as shown below:

$$ \begin{array}{c|c|c|c|c|c|c} \text{Moment} &             {\hat \mu_\text T} &       {\sigma_\text T^2} &      {\hat \mu_\text G} &      {\sigma_\text G^2} &                {\sigma_\text{TG}} &      {\rho_\text{TG}} \\ \hline                 {} & {11.9} &       {335.6} &             {6.80} &                {26.7} &                {14.0} &                {0.1434} \\         \end{array} $$

We need to compare the volatility, interpret the correlation coefficient, and apply bivariate CLT.

Solution

Looking at the output, it is evident that the return from the stock trade is more volatile than the government bond return since it has a higher variance. The correlation between the two forms of return is positive but very small.

If we apply bivariate CLT, then:

$$ \sqrt { n } \left[ \begin{matrix} { \hat { \mu  }  }_{ x }-{ \mu  }_{ x } \\ { \hat { \mu  }  }_{ y }-{ \mu  }_{ y } \end{matrix} \right] \rightarrow N\left( \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right] ,\begin{bmatrix} 335.6 & 14.0 \\ 14.0 & 26.7 \end{bmatrix} \right)  $$

But the mean estimators have a limiting distribution (which is assumed to be normally distributed). So,

$$ \left[ \begin{matrix} { \hat { \mu  }  }_{ x } \\ { \hat { \mu  }  }_{ y } \end{matrix} \right] \rightarrow N\left( \left[ \begin{matrix} { \mu  }_{ x } \\ { \mu  }_{ y } \end{matrix} \right] ,\begin{bmatrix} 0.9589 & 0.04 \\ 0.04 & 0.07629 \end{bmatrix} \right)  $$

Note the new covariance matrix is equivalent to the previous covariance divided by the sample size n=350.

In bivariate CLT, the correlation in the data is the correlation between the sample means and should be equal to the correlation between the data series.

Coskewness and Cokurtosis

Coskewness and Cokurtosis are an extension of the univariate skewness and kurtosis.

Coskewness

The two coskewness measures are defined as:

$$ \text{Skew}(\text X,\text X,\text Y)=\cfrac {\text E[(\text X-\text E[\text X])^2 (\text Y-\text E[\text Y])]}{σ_\text X^2 σ_\text Y } $$ $$ \text {Skew}(\text X,\text Y,\text Y)=\cfrac {\text E[(\text X-\text E[\text X])(\text Y-\text E[\text Y])^2]}{σ_\text X σ_\text Y^2 } $$

These measures both capture the likelihood of the data taking a large directional value whenever the other variable is large in magnitude. When there is no sensitivity to the direction of one variable to the magnitude of the other, the two coskewnesses are 0. For example, the coskewness in a bivariate normal is always 0, even when the correlation is different from 0. Note that the univariate skewness estimators are s(X,X,X) and s{Y,Y,Y).

So how do we estimate coskewness?

The coskewness is estimated by using the estimation analogy. That is, replacing the expectation operator by summation. For instance, the two coskewness is given by:

$$ \text {Skew}(\text X,\text X,\text Y)=\cfrac {\sum_{\text i=1}^\text n (\text x_\text i-\hat \mu_\text X )^2 (\text y_\text i-\hat \mu_\text Y)}{\hat \sigma_\text X^2 \hat \sigma_\text Y } $$ $$ \text {Skew}(\text X,\text Y,\text Y)=\cfrac {\sum_{\text i=1}^\text n (\text x_\text i-\hat \mu_\text X)(\text y_\text i-\hat \mu_\text Y )^2 }{\hat \sigma_\text X \hat \sigma_\text Y^2 } $$

Cokurtosis

There intuitively three configurations of the cokurtosis. They are:

$$ \text {Kurt}(\text X,\text X,\text Y,\text Y)=\cfrac {\text E[(\text X-\text E[\text X])^2 (\text Y-\text E[\text Y])^2]}{\sigma_\text X^2 \sigma_\text Y^2 } $$ $$ \text {Kurt}(\text X,\text X,\text X,\text Y)=\cfrac {\text E[(\text X-\text E[\text X])^3 (\text Y-\text E[\text Y])]}{\sigma_\text X^3 \sigma_\text Y } $$ $$ \text{Kurt}(\text X,\text Y,\text Y,\text Y)=\cfrac {\text E[(\text X-\text E[\text X])(\text Y-\text E[\text Y])^3]}{\sigma_\text X \sigma_\text Y^3 } $$

The reference value of a normally distributed random variable is 3.  A random variable with Kurtosis exceeding 3 is termed to be heavily or fat-tailed. However, comparing the cokurtosis to that of the normal is not easy since the cokurtosis of the bivariate normal depends on the correlation.

When the value of the cokurtosis is 1, then the random variables are uncorrelated and increases as the correlation devices from 0.

Practice Question

A sample of 100 monthly profits gave out the following data:

\( \sum_{\text i=1}^{100} \text x_\text i=3,353\)  and \(\sum_{\text i=1}^{100} \text x_\text i^2=844,536 \)

What is the sample mean and standard deviation of the monthly profits?

A.  Sample Mean=33.53, Standard deviation=85.99

B. Sample Mean=53.53, Standard deviation=85.55

C. Sample Mean=43.53, Standard deviation=89.99

D. Sample Mean=33.63, Standard deviation=65.99

Solution

The correct answer is A.

Recall that the sample mean is given by:

$$ \begin{align*} \hat \mu=\bar X & =\cfrac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i \\ \Rightarrow \bar X & =\frac {1}{100}×3353=33.53 \end{align*} $$

The variance is given by:

$$ \text s^2=\cfrac {1}{\text n-1} \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu)^2 $$

Note that,

$$ (\text X_\text i-\hat \mu)^2=\text X_\text i^2-2\text X_\text i \hat \mu+\hat \mu^2                 $$

So that

$$ \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu)^2 =\sum_{\text i=1}^\text n \text X_\text i^2-2\text X_\text i \hat \mu+\hat \mu^2=\sum_{\text i=1}^\text n \text X_\text i^2-2\hat \mu \sum_{\text i=1}^\text n \text X_\text i+\sum_{\text i=1}^\text n \hat \mu^2 $$

Note again that

$$ \hat \mu=\cfrac {1}{\text n} \sum_{\text i=1}^\text n \text X_\text i\Rightarrow \sum_{\text i=1}^\text n \text X_\text i =\text n \hat \mu $$

So,

$$ \begin{align*} \sum_{\text i=1}^\text n \text X_\text i^2-2\mu ̂\sum_{\text i=1}^\text n \text X_\text i+\sum_{\text i=1}^\text n \hat \mu^2 & =\sum_{\text i=1}^\text n \text X_\text i^2-2\hat \mu.n \hat \mu+n\hat \mu \\ &=\sum_{\text i=1}^\text n \text X_\text i^2-\text n \hat \mu^2  \\ \end{align*} $$

Thus:

$$ \text s^2=\cfrac {1}{\text n-1} \sum_{\text i=1}^\text n (\text X_\text i-\hat \mu)^2 =\cfrac {1}{\text n-1} \left\{ \sum_{\text i=1}^\text n \text X_\text i^2-\text n \hat \mu^2 \right\} $$

So, in our case:

$$ \text s^2=\cfrac {1}{\text n-1} \left\{ \sum_{\text i=1}^\text n \text X_\text i^2-\text n \hat \mu^2 \right\}=\cfrac {1}{99} (844,536-100×33.53^2 )=7395.0496 $$

So that the standard deviation is given to be:

$$ \text s=\sqrt{7395.0496}=85.99 $$