Risk Governance
After completing this reading, you should be able to: Explain Basel regulatory expectations... Read More
After completing this reading, you should be in a position to:
Liquidity refers to a company’s ability to make cash payments as they become due. It is different from solvency, which is the aspect of a company having more assets than liabilities such that its equity value is positive.
Trading liquidity risk is defined as the risk that an institution fails to sell its assets within an appropriate amount of time at a desirable price. Liquidity is measured depending on how quickly an asset can be disposed of at a reasonable price. For instance, an institution, say a bank holding a vast volume of widely-traded, liquid U.S. Treasury Bills in its investment portfolio, has a minimum liquidity risk compared to a bank holding a large volume of thinly-traded, illiquid Non-Agency Mortgage-backed Securities in their investment portfolio.
For a bank to sell an illiquid asset quickly, it should expect to take a loss on the sale due to bigger bid-offer spreads, just like in a fire sale. Some of the factors facilitating liquidity trading risk are predator trading, where markets compete in doing similar trades with each competitor craving for massive profits.
Four factors influence the price at which an asset can be sold. These are:
For a financial instrument where there is no market maker, the implicit bid-offer spread comes in. The bid price decreases while the offer price tends to increase with the size of a trade. For an instrument where there is a market maker, the bids and offers are the same up to the market maker’s size limit and then start to diverge. The following figure illustrates the above:
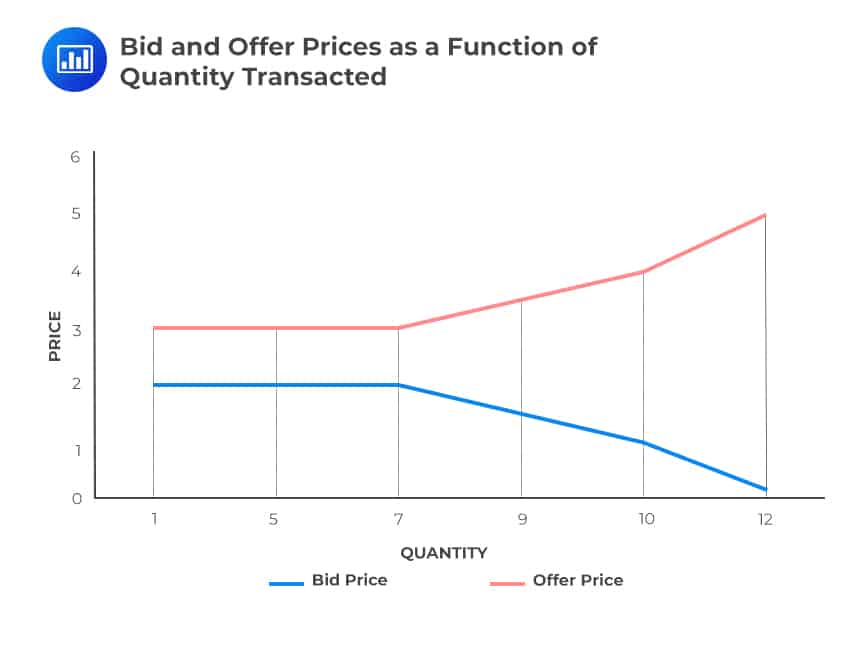 Measuring Market Liquidity
Measuring Market LiquidityThe Bid-offer Spread Measure
The bid-offer spread measure is one of the ways of measuring market liquidity. It can be measured as a dollar amount or a proportion of the asset price. The dollar bid-offer spread is calculated as follows:
$$ \text{p} = \text{Offer price} – \text{Bid price} $$
On the other hand, the proportional bid-Offer spread for an asset is equivalent to:
$$ \text{s}=\cfrac {\text{Offer price}-\text{Bid price}}{\text{Mid-market price}} $$
The mid-market price is halfway between the offer price and the bid price commonly regarded as the fair price. A bank experiences a cost equal to \(\frac {\text{s} \alpha}{2}\), whenever it liquidates an asset position, where α is the dollar (mid-market) value of the position. This fact implies that trades are not done at the mid-market price. Therefore, a buy trade is made at the offer price while a sell trade is made at the bid price.
One way of measuring the liquidity of a book is finding how much it would cost to liquidate the book in normal market conditions within a stipulated time. Supposing that \(\text s_{\text j}\) is an estimate of the proportional bid-offer spread in normal market conditions for the \(\text j_{\text{th}}\) financial security held by a financial institution, and \(\alpha_{\text j}\) is the dollar value of the security’s position, then:
$$ \text{Cost of liquidation (normal market)} =\sum_{\text j=1}^{\text n} \cfrac {{\text S}_{\text j} \alpha_{\text j}}{2} $$
Where n represents the number of positions. It is worth noting that diversification does not necessarily reduce liquidity trading risk. However, \(\text S_{\text j}\) increases with the size of position j. This implies that holding small positions instead of a few large ones entails less liquidity risk. Setting limits to the size of any position can thus, be one way of reducing liquidity trading risk.
Assume that HBC bank has bought 15 million shares of one company and 45 million ounces of a commodity. Further, assume that the shares are bid $90.4, offer $91.6. The commodity is bid $20, offer $ 20.2.
The mid-market value of the position of the shares is equivalent to:
$$ 15×91=$1,365 \text{ million} $$
Note that the mid-market price is halfway between the offer price and the bid price.
The mid-market of the position in the commodity is:
$$ 45×20.1=$904.5 \text{ million} $$
The proportional bid-offer spread for the position of the shares is equivalent to:
$$ \begin{align*} \text{s} & =\cfrac {\text{Offer price}-\text{Bid price}}{\text{Mid-market price}} \\ \text s & =\cfrac {(91.6-90.4)}{91}=0.01318 \\ \end{align*} $$
Similarly, the proportional bid-offer for the position in the commodity is:
$$ \cfrac {(20.2-20)}{20.1}=0.00995 $$
And hence the cost of liquidation in a normal market is:
$$ 1,365×0.01318×0.5+904.5× 0.00995×0.5=$13.495 \text { million} $$
The cost of liquidation in a stressed market within a specified period is another liquidity cost measure.
$$ \text{Cost of liquidation (stressed market)} = \sum_{\text j=1}^{\text n} \cfrac {(\mu_j+\lambda \sigma_{\text j}) \alpha_{\text j}}{2} $$
Where:
\(\mu_{\text j}\) is the mean, while \(\sigma_{\text j}\) is the standard deviation of the proportional bid-offer spread for the \({\text j}_{\text {th}}\) instrument held.
\(\lambda\) is the parameter that gives the required confidence level for the spread. Suppose that we are considering the “worst-case” spreads that are exceeded only 1% of the time, if the spreads are assumed to be normally distributed, then \(\lambda= 2.326\).
Suppose that HBC bank has bought 15 million shares of one company and 45 million ounces of a commodity. Assume that the shares are bid $90.4, offer $91.6. The commodity is bid $20, offer $20.2. The bid-offer spread for the shares has a mean and standard deviation of $1.5 and $1.8, respectively. Further, the mean and standard deviation for the bid-offer spread for the commodity are both $0.14.
The proportional bid-offer spread for the position of shares has a mean of 0.01158 and a standard deviation of 0.02678. On the other hand, the proportional bid-offer spread for the position of the commodity has a mean of 0.004898 and the same standard deviation of 0.004898.
Assuming the spreads follow a normal distribution, calculate the cost of liquidation at the 99% confidence limit.
$$ \begin{align*} & 0.5×1,365×(0.01158+2.326×0.02678) \\ & +0.5×904.5×(0.004898+2.326×0.004898)=57.79 \\ \end{align*} $$
This is more than five times the cost of liquidation in normal market conditions.
The liquidity-adjusted VaR is the regular VaR plus the cost of unwinding positions in a normal market, which is equivalent to:
$$ \text{Liquidity-Adjusted VaR} =\text{VaR}+\sum_{\text j=1}^{\text k} \cfrac {{\text S}_{\text j} \alpha_{\text j}}{2} $$
Alternatively, liquidity-adjusted VaR can also be defined as regular VaR plus the cost of unwinding positions in a stressed market. This is equivalent to:
$$ \text{Liquidity-Adjusted VaR} =\text{VaR}+\sum_{\text j=1}^{\text k} \cfrac {(\mu_j+\lambda \sigma_{\text j}) \alpha_{\text j}}{2} $$
To unwind a strong financial position in a financial instrument, a trader must decide on the best trading strategy to employ. The trader faces a large bid-offer when the position is unwound quickly, but the possible loss from the mid-market price changing against the trader is small. If the trader hesitates from unwinding the position, a low bid-offer accrues with substantial potential loss from the mid-market.
According to Almgren and Chriss, suppose that the size of a position is L units, and a trader gets to decide how to liquidate it over a k-day period. It is convenient to define the bid-offer spread in dollars rather than as a proportion for this case.
Define the dollar bid-offer spread when the trader trades q units in one day as p(q) dollars. Define \(\text q_{\text j}\) as the units traded on day j and \(\text X_{\text j}\) as the size of the trader’s position at the end of day j where \(1 \le j \le k\).
It follows that \(\text x_{\text j}={\text x}_{{\text j}-1}-{\text q_{\text j}}\) for \(1 \le j \le k\) where \(\text x_0\) is defined as the initial position size, L.
Each trade costs half the bid-offer spread, and the total of the costs related to the bid-offer spread is therefore given by:
$$ \sum_{\text j=1}^{\text k} {\text q}_{\text j} \cfrac {{\text p}(\text q_{\text j})}{2} $$
Assume that trading takes place at the start of a day, and the mid-market price movements follow a normal distribution with a daily standard deviation of \(\sigma\). The variance of the change in the value of the traders’ position on day j is \(\sigma^2 {\text x}_{\text j}^2\). If price changes on successive days are independent, the variance of the change in the value of the position applicable to the unwind is:
$$ \sum_{\text j=1}^{\text k} \sigma^2 {\text x}_{\text j}^2 $$
If a trader wishes to minimize VaR, his/her objective should be to choose \(\text q_{\text j}\) such that
$$ \lambda \sqrt{\sum_{\text j=1}^{\text k} \sigma^2 {\text x}_{\text j}^2}+ \sum_{\text j=1}^{\text k} {\text q}_{\text j} \cfrac {{\text p}(\text q_{\text j})}{2} $$
is minimized to
$$ \sum_{\text j=1}^{\text k} {\text q}_{\text j}=\text L $$
When a position is to be closed out over k days, more than 1/k of the position should be traded on the first day as the longer any part of the position is held, the higher the risk of adverse market moves.
Liquidity funding risk is the ability of a financial institution to finance its financial needs when due. Liquidity is different from solvency; a financial institution with a high level of solvency may fall due to lack of liquidity. Factors that may cause liquidity problems in a financial institution include;
It is essential to predict cash needs and ensure that they are realizable in adverse situations to manage liquidity risk.
The core sources of liquidity for a financial institution include:
This source of liquidity is related to liquidity trading risk since a financial institution can meet its funding requirements by liquidating part of its trading book. Therefore, it is significant for a financial institution to quantify the liquidity of its trading book to establish how easy it would be to use the book to raise cash.
Cash is always an available source of liquidity, while treasury securities are issued by countries such as the US and the UK and are quickly convertible into cash within short notice. Although cash and Treasury securities are excellent sources of liquidity, they are expensive as there is a limit to the cash and treasury securities that can reasonably be held by an institution.
Central banks such as the Federal Reserve Board in the United States, the Bank of England in the UK, or the European Central Bank are often referred to as “lenders of last resort.” When banks are experiencing financial challenges, they usually borrow from the central bank.
The capacity to securitize assets is another source of liquidity that has got its challenges. In August 2007, securitization led to liquidity problems whereby banks had entered liquidity backstop arrangements on the asset-backed commercial paper (ABCP) that was used to fund debt instruments, such as mortgages, before their securitization. Failure to find buyers prompted selling institutions to buy instruments themselves. In fact, in some cases, they had to provide financial support to conduits and other off-balance-sheet vehicles that were involved in the securitization This, they did even though they were not legally required to do so.
In stressed market conditions, wholesale deposits can quickly disappear as they are volatile. Similarly, retail deposits are not reliable sources of liquidity. The issue of liquidity funding is hard to achieve as when one financial institution wants to improve its retail or wholesale deposit base for liquidity purposes by offering more attractive rates of interest, others usually want to do the same thing, and hence increased funding becomes hard to realize.
A creditworthy bank usually has no problem in borrowing money, but in stressed market conditions, there is a sensitive aversion to risk leading to higher interest rates, shorter maturities for loans, and in some cases, a complete refusal to provide funds. Financial institutions should monitor the assets that can be pledged as collateral for loans at short notice and invest in such.
As we had highlighted earlier, solvency is very different from liquidity. Solvency reflects the equity status of a financial institution, while liquidity is more critical as it determines a financial institution’s ability to fund its future financial needs when they are due. This is evident through three real cases, as discussed below:
Northern Rock Bank was one of the top five mortgage lenders in the United Kingdom in 2007. It offered deposit accounts, savings account loans, and house/content insurance. The bank was growing rapidly, but at some point, its liquidity position worsened due to its poor sources of liquidity. The bank depended on selling short-term debt instruments for much of its funding, which was not enough to offer stable liquidity.
Consequently, the bank opted for borrowing. It experienced difficulties due to the economic crisis, which were prevailing in 2007. Lenders were not willing to lend because they were very nervous about lending to banks that were heavily involved in the mortgage business.
Though the bank’s assets were enough to cover its liabilities, so it was not insolvent, the inability to fund itself was a severe problem, and it opted to borrow from the Bank of England. However, the fall of the Northern Bank was precipitated by the excessive withdrawals from its clients, which crippled its liquidity status, leading to an increase in emergency borrowing requirements. Finally, the bank could not fund its financial needs, and as a result, it was nationalized, and its management was changed.
The above scenario illustrates how quickly liquidity problems can lead to a bank spiraling downward. If the bank had been managed a little more conservatively and had paid more attention to ensuring that it had access to funding, it might have survived.
Similarly, Ashanti Goldfields of West Africa experienced problems resulting from its hedging program. Following the stressed gold market, the European central banks surprised the market with a declaration that they would limit their gold sales over the subsequent five years.
The price of gold shot up by over 25% and Ashanti was unable to meet margin calls. The company restructured by selling a mine. This led to a dilution of the interest of its shareholders. Additionally, it restructured its hedge positions. In a nutshell, the Ashanti Goldfield closure was due to insufficient liquidity sources.
Metallgesellschaft company is another example of how poor liquidity management can lead to institutions’ closure. Initially, the company was making substantial sales. The company was using long positions in short-dated futures contracts that were rolled forward to hedge against exposure. However, the price of oil dipped, and there were margin calls on the futures positions. MG’s trading became complicated by the fact that its trades were substantial and were anticipated by others. The closure of the institution was due to short-term cash flow pressures, as its liquidity was crippled.
Basel III introduced two liquidity risk requirements, namely; the liquidity coverage ratio (LCR) and the net stable funding ratio (NSFR).
The LCR requirement is expressed as follows:
$$ \cfrac {\text{High-quality liquid assets}}{\text{Net cash outflows in a 30-day period}} \ge 100\% $$
In the calculation of LCR we consider a 30-day period which is one of acute stress involving a downgrade of the following three notches (e.g., from AA+ to A+):
The required LCR was 100% in 2019.
Suppose that ABC bank has high-quality liquid assets that are valued at $50 Million. Additionally, the bank has $30 million in expected net cash flows over a 30-day stress period. The LCR for ABC bank is equivalent to:
$$ \begin{align*} \text{LCR} & =\cfrac {\text{High-quality liquid assets}}{\text{Net cash outflows in a 30-day period}} \\ & =\cfrac {$50}{$30}=167\% \\ \end{align*} $$
Therefore, ABC Bank meets the requirement under Basel III. On the other hand, the NSFR requirement is calculated as follows:
$$ \cfrac {\text{Amount of stable funding}}{\text{Required amount of stable funding}} \ge 100\% $$
The numerator is determined by multiplying each category of funding, such as capital, wholesale deposits, and retail deposits by the available stable funding (ASF) factor, reflecting their stability. On the other hand, the denominator is calculated from the assets and the funded off-balance-sheet items. Note that the above categories are multiplied by a required stable funding (RSF) factor to reflect the permanence of the funding.
The net stable coverage ratio is designed to encourage and incentivize banks to use stable sources to fund activities and reduce dependency on short-term wholesale funding. It aims at mitigating funding risk by reducing maturity mismatches between assets and liabilities on the balance sheet. The ratio has a time horizon of one year and can be calculated as follow:
$$ NSFR = \cfrac {\text{Amount of stable funding}}{\text{Required amount of stable funding}} \ge 100\% $$
The following is a balance sheet for XYZ Bank that separates short-term and long-term assets according to Basel III guidelines. In this case, the short term indicates less than or equal to 30 days, while the long term indicates more than one year. Note that we do not consider durations between these two for simplicity. Additionally, Basel III weighting factors are also included. The Basel III NSFR is calculated using these weighting factors.
Use the balance sheet to evaluate whether the bank meets the Basel III requirements using the NSFR ratio.
$$ \textbf{Balance Sheet for XYZ Bank as at 31 December 2019} $$
$$ \begin{array}{l|c|c|c|c|c} \textbf{Assets} & \textbf{Amount} & \textbf{NSFR} & \textbf{Liabilities} & \textbf{Amount} & \textbf{NSFR} \\ \hline \textbf{Short-Term} & {} & {} & \text{Short-Term} & {} & {} \\ \hline \textbf{Cash} & {0} & {0\%} & \text{Deposits} & {3000} & {80\%} \\ \hline \textbf{T-notes} & {400} & {0\%} & {\text{Deposits Fin} \\ \text{Institutions}} & {1000} & {} \\ \hline \textbf{Loan corporates} & {200} & {85\%} & \textbf{Long-Term} & {} & {} \\ \hline \textbf{Mortgages} & {250} & {65\%} & \text{Owner’s equity} & {1200} & {100\%} \\ \hline \textbf{Corporates} & {100} & {50\%} & \text{Deposits} & {2000} & {100\%} \\ \hline \bf{\text{Loans Fin} \\ \text{Institutions}} & {500} & {0\%} & \text{Unsecured debt} & {3000} & {100\%} \\ \hline \textbf{Long-Term} & {} & {} & {\text{Deposits Fin} \\ \text{Institutions}} & {1200} & {100\%} \\ \hline \textbf{Cash} & {100} & {0\%} & \text{} & {} & {} \\ \hline \textbf{T-notes} & {0} & {0\%} & \text{} & {} & {} \\ \hline \textbf{Loan corporates} & {2500} & {100\%} & \text{} & {} & {} \\ \hline \textbf{Mortgages} & {3500} & {65\%} & \text{} & {} & {} \\ \hline \textbf{Corporates} & {2200} & {100\%} & \text{} & {} & {} \\ \hline \bf{\text{Loans Fin} \\ \text{Institutions}} & {0} & {100\%} & \text{} & {} & {} \\ \end{array} $$
Recall that the NSFR requirement is such that:
$$ \cfrac {\text{Amount of stable funding}}{\text{Required amount of stable funding}} \ge 100\% $$
$$ \begin{align*} & \text{Amount of stable funding is equivalent to:} \\ & =(1200×100\%)+(3000×80\%)+((2000+3000+1200)×100\%) \\ & =9,800 \end{align*} $$
$$ \begin{align*} & \text{The required amount of stable funding is equivalent to:} \\ & (200×85\%)+((250+3500)×65\%)+(100×50\%)+((2500+2200)×100\%)) \\ & =$7,357.5 \end{align*} $$
Therefore:
$$ \text{NSFR} = \cfrac {$9800}{$7,357.5}=133\% $$
NSFR is greater than the required ratio of 100%. Therefore XYZ bank meets Basel III net stable funding requirement.
Bank regulators issued revised principles on how banks should manage liquidity following the 2007 subprime crisis. These are as follows:
A liquidity black hole refers to a situation whereby liquidity has dried up in a market as every participant wants to sell, but no one wants to buy, and vice versa. This situation is also known as a crowded exit. A liquidity black hole is generated when a price decline makes more market participants want to sell, forcing prices well below where they eventually settle. During the sell-off, liquidity dries up, and the asset can be sold only at a fire-sale price.
There exist negative feedback traders and positive feedback traders in a market. The behavior of these traders drives the changes in the liquidity of financial markets. Negative feedback traders usually buy when prices fall and sell when prices rise. On the other hand, positive feedback traders sell when prices fall and buy when prices rise.
Negative feedback traders dominate the trading in liquid markets as these traders buy when the price of an asset gets reasonably low, creating demand for the asset, which restores the price to a reasonable level. The converse is also true. In contrast, positive feedback traders dominate illiquid markets. This is because a fall in the price of an asset causes traders to sell., resulting in a further price fall and more selling. An increase in the asset price causes traders to buy. This causes the price of the assets to increase further and, thus, more buying.
The reasons why positive feedback trading exists include:
Things to Remember
Practice Question
Which of the following correctly explains the phenomenon of liquidity black holes?
A. It is caused primarily by market participants making consistent and identical trading decisions concurrently.
B. It is a situation where central banks globally start tightening liquidity simultaneously.
C. It refers to a situation where there is a sudden drop in the number of market makers.
D. It arises due to informational asymmetries between market participants.
Solution
The correct answer is A.
A is correct: Liquidity black holes arise when a large number of market participants, driven by similar risk management rules or behavioral biases, make concurrent and identical trading decisions, often in response to an external shock. This massive synchronous action can exacerbate market movements and lead to severe liquidity strains, as was the case described by Dr. Henderson.
B is incorrect: While central banks tightening liquidity can cause stress in the financial system, the term “liquidity black holes” specifically refers to the situation arising from market participants’ synchronized actions rather than central bank policies.
C is incorrect: A sudden drop in the number of market makers can indeed reduce liquidity. However, liquidity black holes are primarily about the synchronized behavior of market participants, not just the absence of market makers. Although a reduction in market makers can exacerbate a liquidity event, it is not the primary cause of liquidity black holes.
D is incorrect: While informational asymmetries can lead to market inefficiencies and certain forms of market illiquidity, they are not the central cause behind liquidity black holes. The crux of liquidity black holes is synchronized trading actions by large market participants.
Things to Remember
- Liquidity black holes are primarily driven by the simultaneous and identical trading decisions of a large number of market participants.
- These synchronized actions often arise from shared risk management rules or behavioral biases.
- The phenomenon typically surfaces in response to external shocks, magnifying market movements and causing severe liquidity strains.
- The essence of liquidity black holes is the coordinated behavior of market players rather than external interventions or the presence/lack of market makers.