Learning From Financial Disasters
After completing this reading, you should be able to: Analyze the key factors... Read More
After completing this reading, you should be able to:
Derivatives are contracts that gain their value from the value of financial variables. Financial variables used to trade derivatives are also known as underlying. They include commodity prices, interest rates, oil prices, prices of metals, equity indices, real estate indices, Cryptocurrencies, temperature changes, etc.
Derivatives can either be linear or non-linear.
A linear derivative is one whose value is directly related to the market price of the underlying variable. What does that mean?
If the underlying makes a move, the value of the derivative moves with a nearly identical margin. In fact, there is a 1:1 relationship between the derivative and the underlying – explaining why linear derivatives are said to be “delta-one” products. However, the delta itself need not always be equal to 1. Examples of linear derivatives include futures and forwards.
A non-linear derivative is one whose value/payoff changes with time and space.
Space, in this case, refers to the location of the strike/exercise price with respect to the spot/current price. The payoff varies with the underlying value but also exhibits some non-linear relationship with other variables, including interest rates, dividends, or even volatility. Non-linear derivatives are generally referred to as options.
For non-linear derivatives, the delta is not constant. Rather, it keeps on changing with the change in the underlying asset. Examples include the Vanilla European option, Vanilla American option, Bermudan option, etc.
Derivatives are majorly used to hedge or to speculate. The following are specific examples of the uses of derivatives.
In the over-the-counter market, trading occurs between participants who contact each other directly or through a broker. Participants may be able to trade privately without the other party being aware of the terms, including the price. Stocks traded in an OTC market could belong to a small company that’s yet to satisfy the conditions for listing on the exchange. The OTC market is also popular for large trades.
Since the 2007-2009 financial crisis, OTC markets are, however, increasingly being regulated. Some of the regulations include:
Investors trade in contracts that have been identified in the exchange. Traditionally trading was done using the outcry system (Investors met at the exchange floor and used signals to indicate their proposed trades.) Currently, trading is done electronically through a computer.
The years 1997-2017 saw the exchange-traded market and the OTC markets growing by a factor of 6 and 7.4, respectively.
An option contract is an agreement between two parties to transact on underlying security at a predetermined price called the strike price before some date called the expiration date. The option gives the holder a right but not the obligation to buy/sell the underlying at an agreed-upon date at the strike price.
Options not only hedge against risk but also provide additional protection against adverse price movements. In other words, they protect against negative risk while preserving upward payoffs.
All European options can only be exercised at maturity. On the other hand, American options may be exercised any time between the issue date and expiration. As such, the price of an option is directly proportional to its maturity date. For example, the premium paid for an out-of-the-money option on Apple expiring in one month will be less than the premium paid for an option with the same strike price expiring in one year.
A call option gives the holder the right but not the obligation to buy the underlying asset at the strike price before the expiration date. On the other hand, a put option gives the holder the right but not the obligation to sell the underlying asset at the strike price before the expiration date.
Consider a European call option on a stock that will be exercised at time \(T\). Let K be the strike price, and \(S_T\) be the stock price at time \(T\). Consider the buyer of the call option (long position in the call option). By definition, the buyer will exercise the option if \(S_T>K\) and thus the payoff of the buyer is \(S_T-K\). Intuitively, if \(S_T < K\) the option is not exercised, and thus the payoff to the buyer is 0.
The payoff to the buyer and seller is summarized below:
To the buyer (long position in the call option),
$$ { C }_{ T }=max\left( 0,{ S }_{ T }-K \right) $$
Where:
\({ C }_{ T }\) = call option payoff at time T.
\({ S }_{ T }\) = stock price at maturity.
\(K\) = strike price
The graph of the payoff of a long position in the call option is shown below:
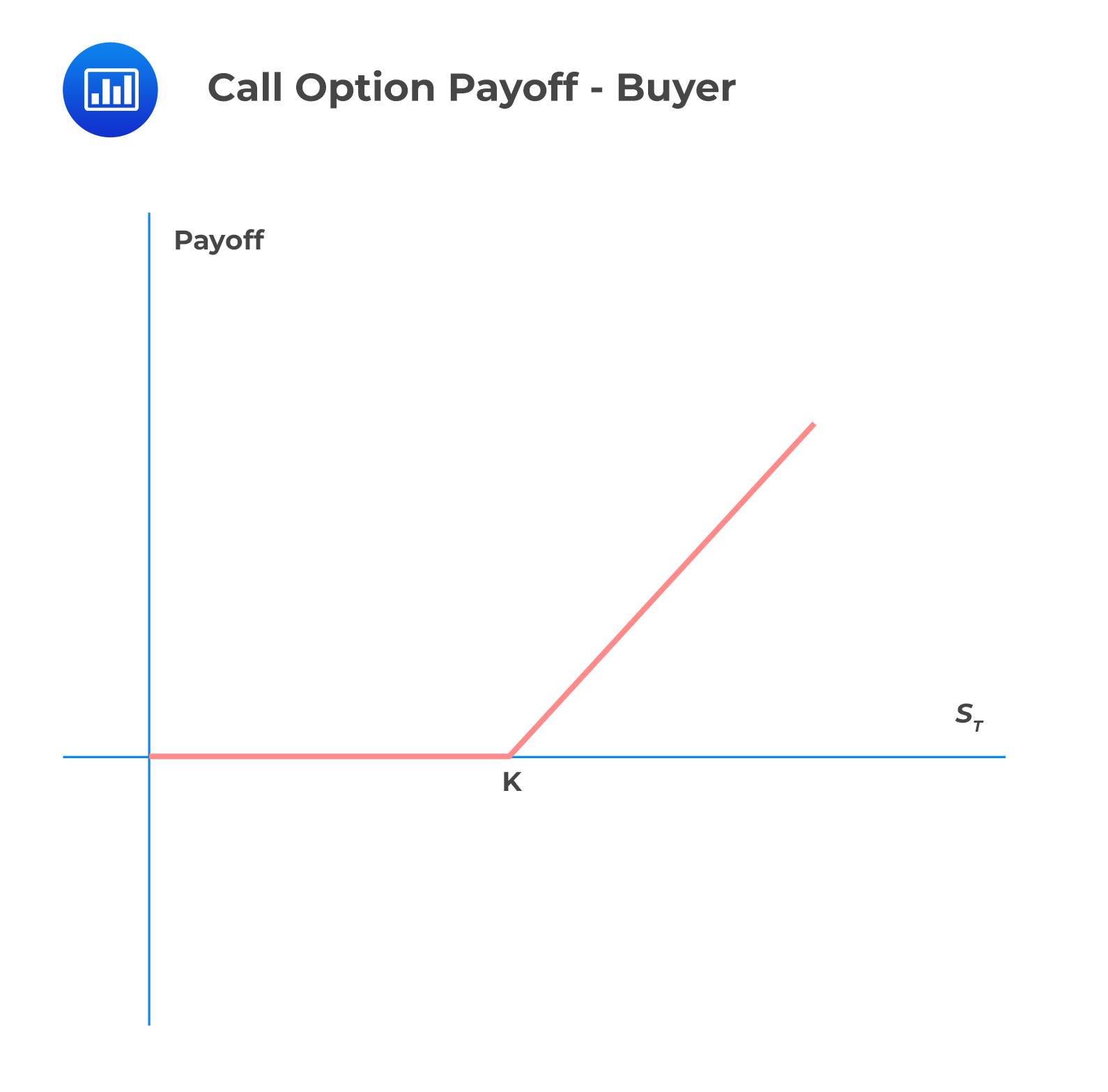 To the seller, payoff =\(-{ C }_{ T }\). The payoff of the short position in the call option is shown below:
To the seller, payoff =\(-{ C }_{ T }\). The payoff of the short position in the call option is shown below:
 The price paid for the call, \({ C }_{ 0 }\) is also called the call premium.
The price paid for the call, \({ C }_{ 0 }\) is also called the call premium.
Thus,
Profit to the call option buyer =\({ C }_{ T }-{ C }_{ 0 }\)
Profit to the call option seller =\({ C }_{ 0 }-{ C }_{ T }\)
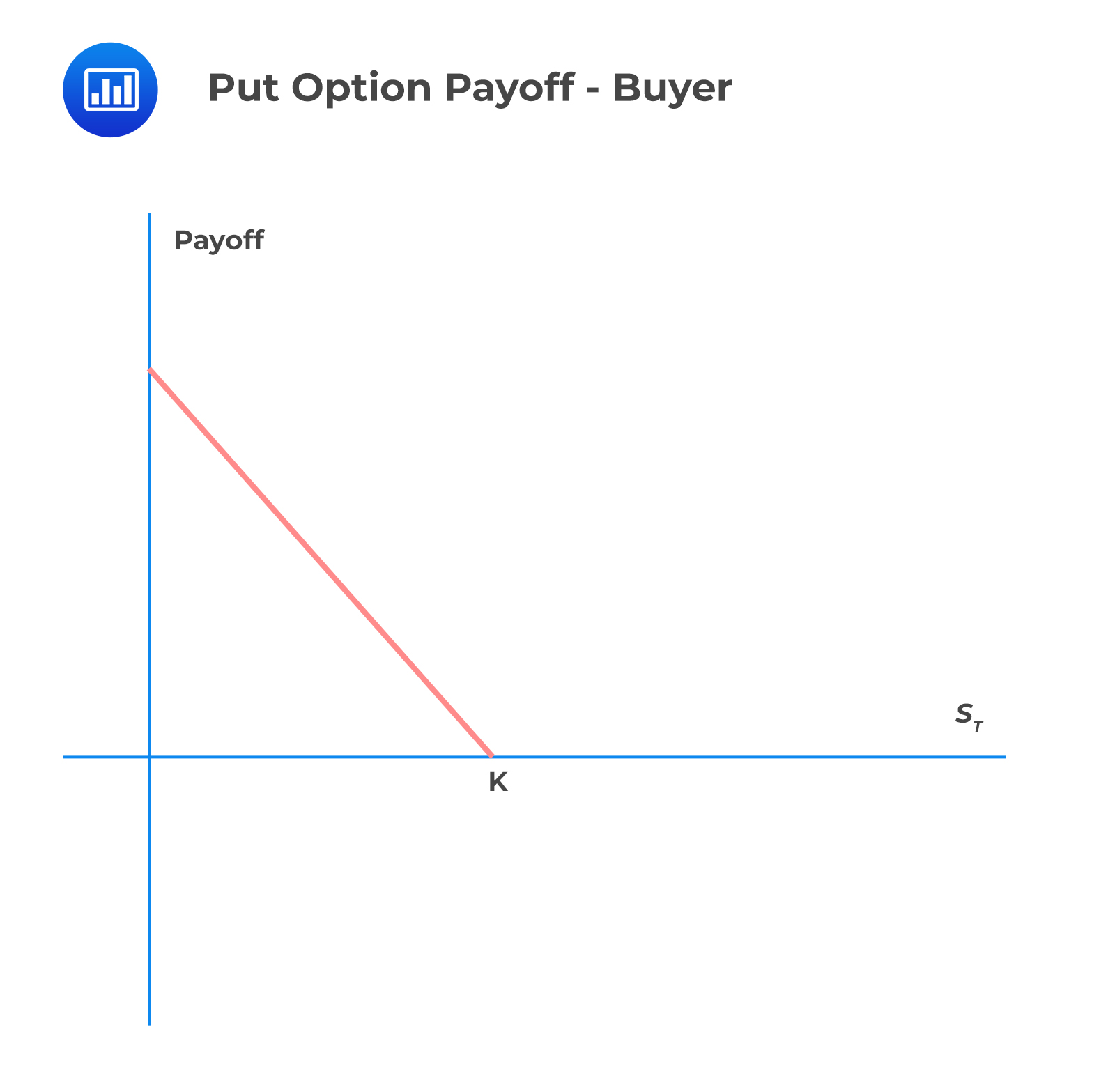
Using the same variables as a call option, and by definition of a put option, the European put option is exercised if \(S_T < K\). In other words, the buyer of the option has the right to sell the stock for \(K\). Therefore, if exercised, the payoff to the buyer (long position in the put option) is \(K-S_T\). Intuitively, the put option is not exercised if \(S_T > K\) and thus, the option is worthless to the buyer.
The payoff to the buyer and seller is summarized below:
To the buyer (long position in the put option),
$$ { P }_{ T }=max\left( 0,X-{ S }_{ T } \right) $$
Where:
\({ P }_{ T }\)=put option payoff.
\({ S }_{ T }\)=stock price at maturity.
\(X\)=strike price.
The payoff of a long put is shown in the following graph:
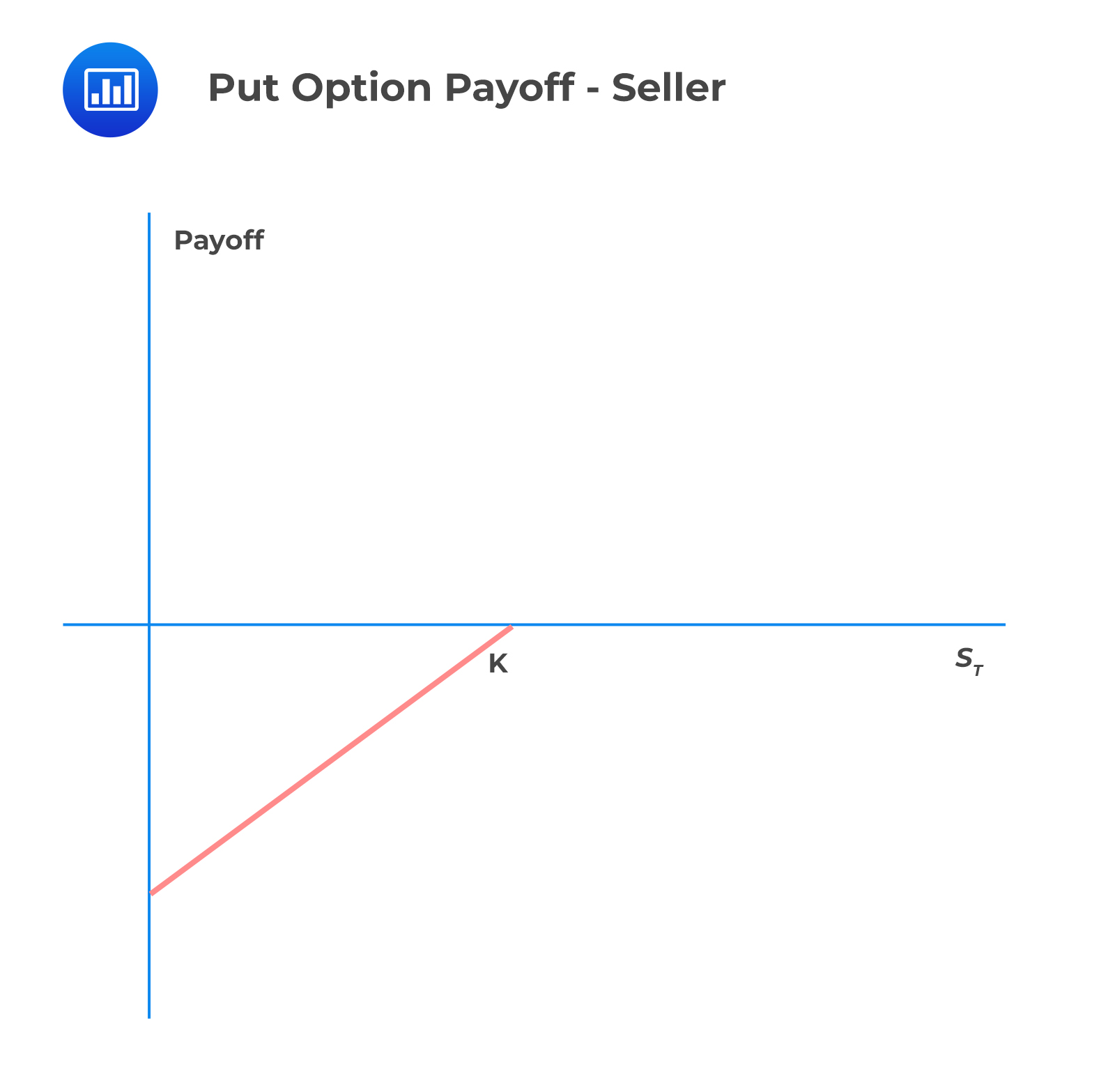
 To the seller(short position in the put option),
To the seller(short position in the put option),
payoff =\(-{ P }_{ T }\).
The graph of the short put is shown below:
 The price paid for the put, \({ P }_{ 0 }\) is also called the put premium.
The price paid for the put, \({ P }_{ 0 }\) is also called the put premium.
Thus,
Profit to put option buyer =\({ P }_{ T }-{ P }_{ 0 }\)
Profit to the put option seller =\({ P }_{ 0 }-{ P }_{ T }\)
A forward contract is a non-standardized contract – traded in an over-the-counter market –between two parties that specifies the price and the quantity of an asset to be delivered in the future. That it’s non-standardized implies it cannot be traded on an exchange. Instead, they are traded in the OTC market. One party takes a long position and agrees to buy the underlying asset at a specified price on the specified date, while the other party takes a short position and agrees to sell the asset on that same date at that same price.
The agreed-upon price is called the forward price. The price at which the dealer wants to buy is called the bid price, while the price the dealer wants to sell is called the ask price.
Exam tips:
The bid price is the “quoted bid,” or the highest price, which a dealer is willing to pay to purchase a security. The offer price is the price at which the security is offered for sale, also known as the “asking price.” The bid-ask spread represents the difference between the offer price and the bid price.
Consider a forward contract on a Stock. Let \(S_T\) be the stock price at the maturity of and K be the delivery (forward price at the initiation of forward contract). The payoff of the long and short positions is given below.
The payoff to the long position (the buyer of the forward contract) is given by:
Payoff = \(S_T-K\)
Where:
\(S_T\)= spot stock price at maturity of the forward contract.
\(K\) = delivery price.
The payoff to the short position (seller of the) = \(K-S_T\) Consider the following diagram:
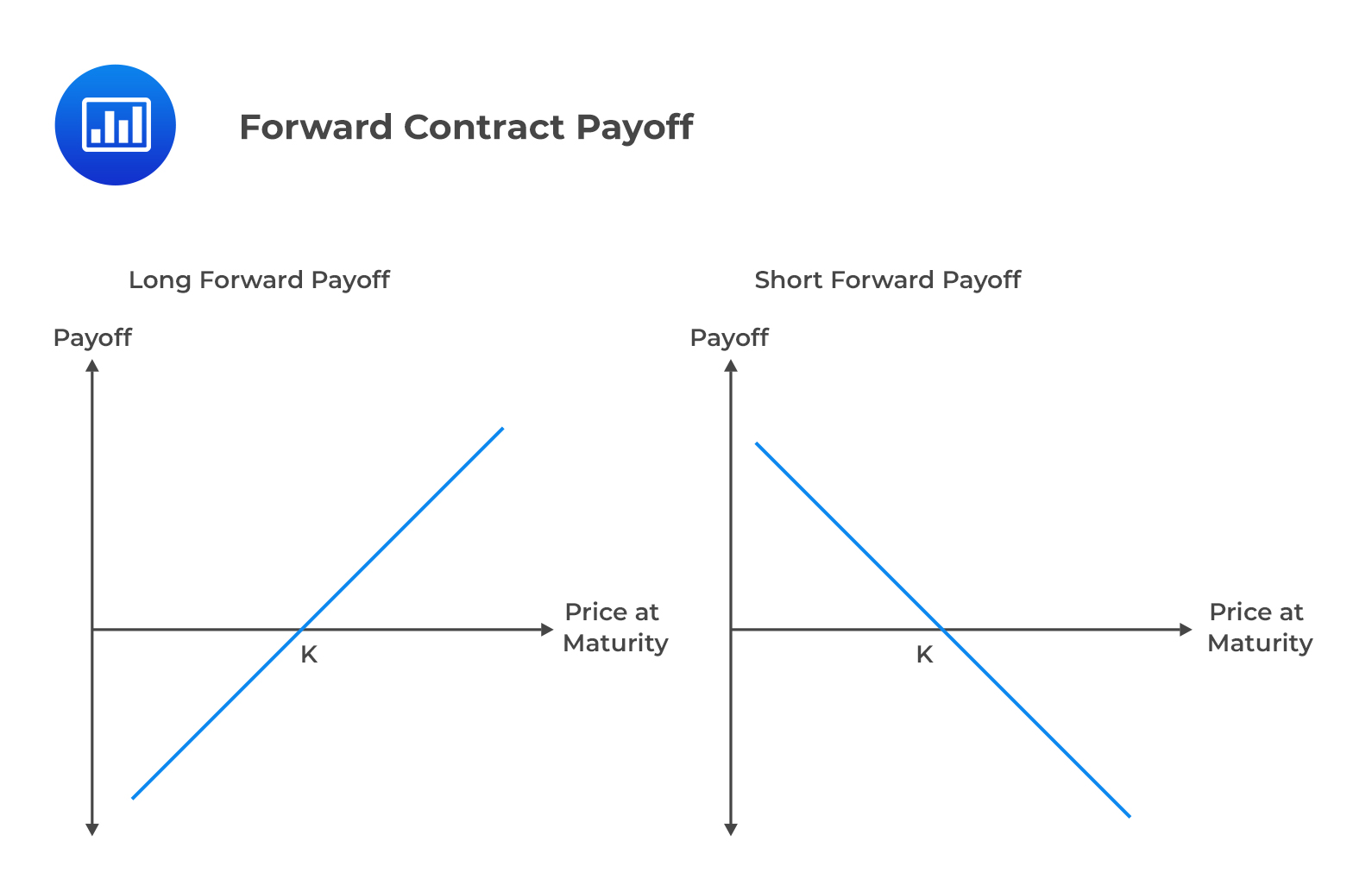 The graphs above imply that for a trader in a long position, the payoff () will be beneficial when the underlying price (which is the stock price in our case) is high. On the other hand, for a trader in a short position, the payoff will be beneficial with a lower underlying price.
The graphs above imply that for a trader in a long position, the payoff () will be beneficial when the underlying price (which is the stock price in our case) is high. On the other hand, for a trader in a short position, the payoff will be beneficial with a lower underlying price.
Example: Calculating the Payoff of a Forward Contract
Consider the forward contract on CAD- EUR exchange rate. The spot bid and ask prices per one euro are CAD 1.1080 and CAD 1.1083, respectively. The 6-month bid and ask prices are CAD 1.1120 and CAD 1.1125, respectively.
Suppose that company X enters into a long position to buy 10 million euros in six months. If the actual CAD- EUR exchange rate in six months is CAD 1.1200 per euro, calculate the profit to company X.
Solution
Based on the 6-month bid-ask exchange rates, company X buys 10 million euros for CAD 1.1125 (that is \(K=1.1125\)). Consequently, the profit made by company X is
$$10,000,000\times (1.120-1.1125) = \text{USD}75,000$$
Note: The short position of the above made a transaction made a loss of:
$$10,000,000\times (1.1125-1.1200) = -\text{USD}75,000$$
A futures contract is a standardized, legally binding agreement – traded in on an exchange – between two parties that specifies the price to trade a given asset (commodity or financial instrument) at a specified future date.
Note that future contracts offer payoffs similar to forward contracts. However, futures contracts trade on exchanges; that is, the underlying asset and possible maturity date are clearly stated in the contract.
Futures contracts differ from forwards in several other aspects:
Hedging is the use of derivatives like futures and options to reduce or eliminate financial exposure. Before delving further into hedging, it is imperative to understand the following points:
An investor with a long position in an asset can hedge the exposure by entering into a short futures contract or buying a put option. An investor with a short position in an asset can hedge the exposure by entering into a long futures contract or buying a call option.
A forward contract helps the hedger to lock in the price of the underlying security. Forward contracts do not need any investment at the onset. However, the hedger gives up any movement that may have had positive results if they left the position unhedged. Let us look at an example:
Suppose a U.S.-based company is scheduled to receive £10 million in six months. The current exchange rate stands at 1.32$/£. The management is worried that the pound might depreciate against the dollar. It decides to hedge the exchange risk with a forward contract at 1.3$/£.
With the forward, the company will be guaranteed to receive $13million ( =£10m×1.3$/£). Suppose the company does not hedge the position and the exchange rate in six months turns out to be 1.25$/£. The company will receive $12,500,000. Suppose further that the company does hedge the position at 1.3$/£, and the rate turns out to be 1.35$/£. In this case, the company will still receive $13 million but will be forced to give up the extra $500,000 it would have received if it did not hedge the position in the first place.
The most common categories of market participants are:
Hedgers use derivatives to reduce or remove risk exposure. We have already discussed how hedging works above. Consider the following example where foreign exchange risk is hedged using options.
Example: Hedging Exchange Rate Risk Using Options
A risk manager in company X (located in the U.S.) knows that his company is due to pay 10 million euros in 6 months, at the exchange rate of USD 1.1120 per euro. How can the risk manager hedge again foreign exchange risk using a call option?
Solution
The risk manager can hedge against the foreign exchange risk by buying the call option with a strike price of USD 1.1120. If in six months the exchange rate is more than USD 1.1120, the risk manager will exercise the option, getting the 10 million euros using the exchange rate of USD 1.1120.
If the exchange rate is less than USD 1.1120, the risk manager will not exercise the option and consequently acquiring the 10 million euro at a lower exchange rate.
If now, the risk manager’s company is due to receive 10 million euros in six months, at a USD 1.112O exchange rate. How can the risk manager this position against the foreign exchange rate?
Alternatively, the risk manager could buy the European put option to sell 10 million euros at an exchange rate of USD 1.1120. If in six months the exchange is less than USD 1.1120, the risk manager exercises the option by selling the received for USD 1.1120. On the other hand, if the exchange is greater than USD 1.1120, the option is not exercised, and the risk manager acquires a favorable exchange rate.
Speculative trading (regarding futures contracts) refers to the trading of futures contracts without the intention of obtaining the underlying commodity. Thus, speculators basically make bets on the market, unlike hedgers, whose priority is to eliminate exposures.
Speculators are motivated by the leverage that comes with futures contracts in which no initial investment is required. All that’s needed is the initial margin required by the clearinghouse/exchange. The margin is no more than a percentage of the notional value of the underlying. The gains or losses associated with futures can be quite large, and payoffs are symmetrical.
Speculators trade in futures, intending to resell these contracts before maturity. They expect the futures price to move in their favor and make a profit when selling the contracts. However, there can be no guarantees that the price will move in their favor, and therefore this trading strategy is also laden with risks. If the price moves against a speculator’s position, they could suffer substantial losses.
For options, speculators only need to part with the option’s price at the onset, often just a few dollars for 100 shares worth of the underlying. However, options have asymmetrical payoffs. Going long on options can bring in significant gains, but losses are limited to the option’s price paid.
In a nutshell, speculators buy assets for time and apply different strategies to benefit from price changes.
Example: Profit from Speculation
The current stock price is CAD50, and speculators believe that in one month, this price would have increased to at least CAD55. Moreover, the call option on the stock has a strike price of CAD52 with a price of CAD2. For convenience, assume that each call option represents 1 share of the underlying stock.
The speculator has an initial capital of CAD5000. If, at the end of one month, the stock price is CAD56, which strategy is more profitable?
Solution
For strategy I, the profit made is given by:
$$(56-50)\times 100 = \text{CAD} 600$$
For strategy II, the profit made is given by:
$$[2,500\times\left(56-52\right)] – 5000=\text{CAD} 5,000$$
Hence it is more profitable to purchase call options.
Arbitrage opportunities exist when prices of similar assets are set at different levels. Therefore, an arbitrageur attempts to make a risk-free profit by buying the asset in the cheaper market and simultaneously selling it in the overpriced market.
For example, suppose ABC stock is trading at $200 on exchange A and $198 on exchange B. Then, if you buy one ABC stock on exchange B and simultaneously sell it on exchange A, you can make a risk-free profit of $2 without any outlay of cash.
However, arbitrage opportunities are normally short-lived. The nature of efficient markets is that market forces will push up the asset’s price in the underpriced market while simultaneously pushing down the asset’s price in the overpriced market. At the end of the day, the asset will be priced equally in both markets.
There are no guarantees the market price will move in favor of the derivative trader. For example, an investor who is short in a put option has no guarantees that the underlying price will stay above the strike price, allowing them to keep the premium. The underlying’s price could as well fall below the strike, in which case the option buyer exercises the option, forcing the seller to buy a stock at a price that’s higher than its market price.
There’s always the risk that the buyer, seller, or dealer will default on the contract. This risk is particularly prevalent in OTC markets where regulations are not as strict as in exchange.
Closing out a deal prior to maturity, e.g., in an American option that can be exercised before maturity, can at times be difficult. Even more likely, bid-ask spreads could be so large as to represent a substantial cost.
There’s always the risk that a trader with instructions to use derivatives as a hedging tool will be tempted to take speculative positions, possibly in the hope of making a “kill’. Such a move can be disastrous for the firm.
Question
Which of the following characteristics is a defining feature of non-linear derivatives (such as a European call option) in comparison to linear derivatives (such as a forward contract)?
- Non-linear derivatives always have positive values.
- Non-linear derivatives have a constant rate of change in value with respect to changes in the underlying asset.
- Non-linear derivatives have an asymmetrical payoff profile, allowing for limited loss with unlimited potential gain.
- Non-linear derivatives require an upfront premium to be paid by both parties involved in the contract.
Solution
The correct answer is C.
Non-linear derivatives, such as options, have an asymmetrical payoff profile. This characteristic means that the holder of the option can have limited loss (the premium paid for the option) with the potential for unlimited gain. In the case of a European call option, if the price of the underlying asset goes above the strike price, the holder can exercise the option and make a profit. If the price stays below the strike price, the holder’s loss is limited to the premium paid. This is a distinguishing feature of non-linear derivatives.
A is incorrect because non-linear derivatives do not always have positive values. For example, an option can be worthless if it is out-of-the-money at expiration.
B is incorrect because non-linear derivatives do not have a constant rate of change in value with respect to changes in the underlying asset. The change in value can be more pronounced as the price of the underlying asset moves further in or out-of-the-money. This is in contrast to linear derivatives like forward contracts, where the change in value is linear with respect to changes in the underlying asset.
D is incorrect because non-linear derivatives do not require an upfront premium to be paid by both parties. Generally, only the buyer of the option pays a premium, while the seller receives it. In contrast, linear derivatives like forward contracts typically do not involve the payment of a premium by either party.
Things to Remember
- Non-linear derivatives, such as options, have an asymmetrical payoff profile, which is their distinguishing feature.
- The asymmetry in the payoff profile allows for limited loss (the premium paid) with unlimited potential gain.
- In options, such as a European call option, the potential loss is capped at the premium paid, while gains can be unlimited if the underlying asset’s price moves favorably.
- This characteristic contrasts with linear derivatives like forward contracts, where the change in value is linear and symmetrical with respect to changes in the underlying asset.