Empirical Approaches to Risk Metrics and Hedging

After completing this reading, you should be able to:

• Explain the drawbacks to using a DV01-neutral hedge for a bond position.
• Describe a regression hedge and explain how it can improve a standard DV01-neutral hedge.
• Calculate the regression hedge adjustment factor, beta.
• Calculate the face value of an offsetting position needed to carry out a regression hedge.
• Calculate the face value of multiple offsetting swap positions needed to carry out a two-variable regression hedge.
• Compare and contrast level and change regressions.
• Describe the principal component analysis and explain how it is applied to constructing a hedging portfolio.

The Drawbacks to Using a DV01-neutral Hedge for a Bond Position

Whereas the standard DVO1-neutral hedge assumes that the yield on a bond and the yield on a hedging instrument rise and fall by the same number of basis points, the reality is that a one-to-one yield relationship does not always exist.

For example, consider a trader who owns a T-bond that uses a nominal yield. The trader wishes to hedge the bond with a Treasury Inflation-Protected Security (TIPS) which uses a real yield. This hedge will make sure that the trader will neither make nor lose money should the TIPS and the nominal bond either increase or decrease by a similar number of basis points. Although the hedge will largely be effective, it will likely be imprecise when changes in yield occur. Historical evidence strongly suggests that nominal yield adjusts by more than one basis point for every basis point adjustment in the real yield.

In general, hedging tools based on DV01 assume that yields on nominal bonds and TIPS change by the same amount, but this assumption does not hold in practice.

To produce a more realistic hedge, regression analysis techniques are used to make adjustments to the DV01 hedge.

Regression Hedge

A DV01-neutral hedge is imperfect because nominal yield adjusts by more than one basis point for every basis point adjustment in the real yield. The implication is that the values of the initial position and the hedge will not move in line given a change in interest rates. A regression hedge solves this problem by taking DV01 -style hedges and adjusting them to projected nominal yield changes compared to projected real yield changes. The regression hedge uses least-squares analysis to establish a relationship between real and nominal yields. A trader is, therefore, able to estimate how much the nominal yield changes, on average, given a change in the TIPS yield.

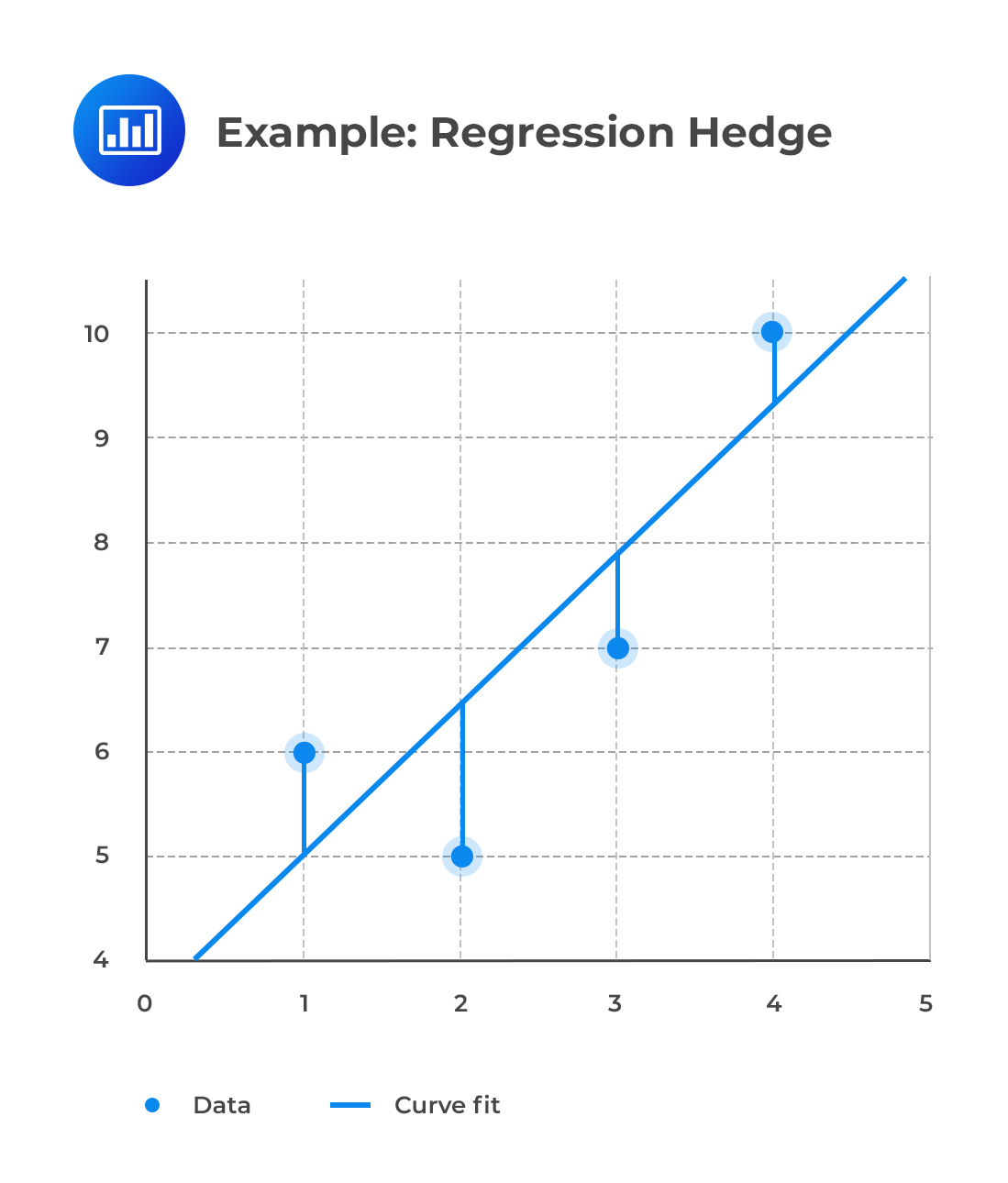Example: Standard DV01-neutral Hedge

A trader plans to short $100 million of the (nominal) \(3\frac { 5 }{ 8 } \) s of August 15, 2019, and, against that, to buy some amount of the TIPS \(1\frac { 7 }{ 8 }\) s of July 15, 2019 (which makes inflation-adjusted payments) to hedge the T-bond. The initial spread between these two securities represents the current views on inflation. Over time, changes in yields on nominal bonds and TIPS do not move in line; the changes do not track one-to-one. To illustrate this hedge, let’s assume we have the following data for yields and DVO1s of the two positions.

$$\begin{array}{c|c|c} \textbf{Bond} & \textbf{Yield} & \textbf{DV01} \\ \hline \text{TIPS} & {1.238} & {0.083} \\ \hline {\text T-\text{BOND}} & {3.272} & {0.067} \\ \end{array}$$

The big question here is: What amount of the long position (TIPS) does the trader need to buy so as make the position DV01-neutral?

A hedge ratio determines the amount of par of the hedge position that needs to be bought or sold for every $1 par value of the nominal position (T-bond).

$$ \begin{align*} \text{HR} & =\cfrac {\text{DV01 of nominal bond}}{\text{DV01 of real bond}} \\ & =\cfrac {0.067}{0.083}=0.8072 \\ \end{align*}$$

For every $1 par value of the T-bond, therefore, the trader needs to go long $0.81 of par of the TIPS – the real yield bond. For $100 million par value, therefore, the face amount needed is $81 million.

$$ \text{Face amount} = 100\text{ million} * 0.81 = $81 \text{ million} $$

As noted earlier, the problem with the DV01-neutral approach is that it implicitly assumes that the T-bond and the TIPS are perfectly co-dependent, meaning they move 1:1. In reality, the two move disproportionately.

To improve this hedge by least squares regression, the trader would need to gather yield data over time and plot a regression line, with the real yield as the independent variable and the nominal yield as the dependent variable.

To compensate for the disproportionate change in the nominal yield for a given change in the real yield, the trader would adjust the DV01-neutral hedge.

For example, if the yield in the data changes by 1.0165 basis points per basis-point change in the real yield, the trader could adjust the hedge such that:

$$ \text{Face amount} = 100 \text{ million} * 0.81 * 1.0165 = $82.34 \text{ million} $$

A 1:1 standard hedge results in a DV01 hedge of $81 million of the TIPS, but the regression hedge increases this amount to $82.34 million to compensate for the fact that, on average, the nominal yield changes by more than one basis point for every basis-point change in the real yield.

Calculating the Regression Hedge Adjustment Factor, Beta

In order to come up with an effective hedge, we must come up with a linear relationship between the real yield and nominal yield.

If \(\Delta \text y_\text t^\text R\) and \(\Delta \text y_\text t^\text N\) represent the changes in the yields of the real and nominal bonds, respectively, and assume that:

$$ \Delta \text y_\text t^\text N=\alpha+\beta \Delta \text y_\text t^\text R+\epsilon_\text t $$

According to the equation, the changes in the real yield, the independent variable, are used to predict changes in the nominal yield, the dependent variable.

Least squares regression is used to analyze these changes and estimate the values of the intercept, \(\alpha\), and the slope parameter, \(\beta\).

The error term \(\epsilon_\text t\) is the deviation of the nominal yield change on a particular day from the change predicted by the model.

Although the regression beta (slope) can change over time, it paints a more realistic picture than the DV01-based hedge does.

Example: Calculating the Predicted Change in Nominal Yield

An analyst wishes to establish the relationship between the real and nominal yield. After the least-squares regression analysis, they establish that the parameters estimated with the data, denoted \(\hat \alpha\) and \(\hat \beta\), are 0 and 1.04 respectively. If \(\Delta \text y_\text t^\text R\) is 5 basis points on a particular day, determine the predicted change in the nominal yield, assuming that the error term is zero.

Solution

A beta of 1.04 means that over the sample period, the nominal yield increases by 1.04 basis points for every basis point increase in real yield.

$$ \Delta \text y_\text t^\text N=\alpha + \beta \Delta \text y_\text t^\text R+\epsilon_\text t=0+1.04(5)+0=5.2 $$

Thus, the nominal yield changes by 5.2 basis points on that particular day.

Example: Estimating the Value of the Error Term

An analyst wishes to establish the relationship between the real and nominal yield. After the least-squares regression analysis, they establish that the parameters estimated with the data, denoted \(\hat \alpha\) and \(\hat \beta \), are 0 and 1.04 respectively. On a particular day, the observed change in real yield, \(\Delta \text y_\text t^\text R\), is 5 basis points, while the predicted change in the nominal yield, \(\Delta \text y_\text t^\text N\), is 5.3 basis points. Determine the realized error that day.

Solution

$$ \begin{align*} \Delta \text y_\text t^\text N & =\alpha + \beta \Delta \text y_\text t^\text R+\epsilon_\text t \\ 5.3 & =0+1.04(5)+\epsilon_\text t \\ \end{align*} $$

\(\epsilon_\text t\)=0.1 basis points.

An advantage of the regression hedge is that the trader may estimate how much the nominal yield changes, on average, given a change in the TIPS yield. Further, it automatically provides an estimate of the volatility of the hedged portfolio:

$$ \text{Standard deviation} (\text{volatility}) \text{ of portfolio} = \text F^\text N×\cfrac {\text{DV}01^\text N}{100} {\hat \sigma} $$

where:

\(F^N\) = Face amount of the nominal bond.

\(DV01^N\) = DV01 of the nominal bond.

\(\hat \sigma\)= Standard error of regression.

Calculating the Face Value of an Offsetting Position Needed to Carry Out a Regression Hedge

We use the regression beta (slope) as an adjustment factor, to improve on the DV01- neutral hedge.

To determine the face amount of the hedge, we use the following relationship:

$$ \text F^\text R=-\text F^\text N \left[\cfrac {\text{DV01}^\text N}{\text{DV01}^\text R} \right] \beta $$

Where:

\(\text F^\text R\) = Face amount of the real bond.

\(\text F^\text N\) = Face amount of the nominal bond.

\(\text{DV01}^\text R\) = DV01 of the real bond.

\(\text{DV01}^\text N\) = DV01 of the nominal bond.

\(\beta\) = Slope coefficient in regression.

Note that we can also express the above relationship as:

$$ \text F^\text R=-\text F^\text N [\text{Hedge Ratio}]\beta $$.

Example: Calculating the Face Value of the Hedge

A trader plans to short $100 million of a Treasury bond and, against that, to buy some amount of the TIPS (which makes inflation-adjusted payments) to hedge the T-bond. The following data exists for yields and DVO1s of the two positions:

$$ \begin{array}{c|c|c} \textbf{Bond} & \textbf{Yield} & \textbf{DV01} \\ \hline \text{TIPS} & {1.335} & {0.08} \\ \hline \text{T-BOND} & {2.425} & {0.05} \\ \end{array} $$

Empirical studies have established the following relationship between the real yield and nominal yield.

$$ \Delta \text y_\text t^\text N =1.0165\Delta \text y_\text t^\text R+\epsilon_\text t $$

Determine the face amount of the TIPS required to hedge the T-bond position.

Solution

To determine the face amount of the hedge, we use the following relationship:

$$ \text F^\text R=-\text F^\text N \left[\cfrac {\text{DV01}^\text N}{\text{DV01}^\text R} \right] \beta $$

Where:

\(\text F^\text R\) = Face amount of the real bond.

\(\text F^\text N\) = Face amount of the nominal bond.

\(\text{DV01}^\text R\) = DV01 of the real bond.

\(\text{DV01}^\text N\) = DV01 of the nominal bond.

Thus,

$$ \text F^\text R=-(-100) \left[\cfrac {0.05}{0.08} \right]1.0165=63.53 $$

This regression hedge suggests that for every $100 million sold in T-bonds, we should buy $63.53 million in TIPS. This will account for hedging differences between nominal and real yields over time.

Calculating the Face Value of Multiple Offsetting Swap Positions Needed to Carry Out a Two-variable Regression Hedge

We can also carry out regression hedging with two variables. The two-variable case is quite similar to the one-variable case but there are some exceptions.

To see how this works, assume that a trader in interest rate swaps buys/receives the fixed rate in a 20-year swap from a customer and wishes to hedge this interest rate exposure. In these circumstances, the trader can achieve their goal by coming up with a regression hedge with swaps of different maturities. However, immediate hedging of the position by selling 20-year swaps may not be practical because such a move would sacrifice too much if not all the spread paid by the customer. A plausible alternative might be to sell a combination of 10- and 30-year swaps.

In this case, multiple regression analysis will be needed because we need to approximate the relationship between changes in 20-year swap rates and changes in 10- and 30-year swap rates. The following regression equation describes this relationship:

$$ \Delta \text y_\text t^{20}=\alpha +\beta^{10} \Delta \text y_\text t^{10}+\beta^{30} \Delta \text y_\text t^{30}+\epsilon_\text t $$

Next, are the initial regression analysis results using data on changes in the 10-, 20-, and 30-year swap rates for a five-year time period.

The hedge can be expressed in terms of risk weights (the DV01 risk in the 10-year part of the hedge and the DV01 risk in the 30-year part of the hedge can both be expressed as a fraction of the DV01 risk of the 20-year). These risk weights are the beta coefficients in the regression equation:

$$ \begin{align*} & \cfrac {-\text F^{10}×\text{DV}01^{10}}{\text F^{20}×\text{DV}01^{20}} = \text{Change in 10-year swap rate}, \beta^{10} \\ & \cfrac {-\text F^{30}×\text{DV} 01^{30}}{\text F^{20}×\text{DV}01^{20} } = \text{Change in 30-year swap rate}, \beta^{30} \\ \end{align*} $$.

$$ \begin{array}{c|cc} \text{Number of observations} & {1281} & {} \\ \hline \text{R-squared} & {99.8\%} & {} \\ \hline \text{Standard error} & {0.14} & {} \\ \hline \textbf{Regression Coefficients} & \textbf{Value} & \textbf{Standard Error} \\ \hline \text{Alpha} & {-0.0014} & {0.0040} \\ \hline \text{Change in 10-year swap rate} & {0.2221} & {0.0034} \\ \hline \text{Change in 30-year swap rate} & {0.7765} & {0.0037} \\ \end{array} $$

Interpreting the Table:

The results suggest that given an illiquid 20-year swap, a trader would hedge 22.21% of the 20-year swap DV01 with a 10-year swap and 77.65% of the 20-year swap DV01 with a 30-year swap. And since these weights sum up to 99.86% which is very close to 1, the regression hedge will be very close to the 20-year swap DV01.

Also noteworthy is the R-squared value. A combination of the change in the 10-year and 30-year swap rates explains 99.8% of the change in the 20-year swap rate.

Level versus Change Regressions

When constructing regression hedges, two methods have been put forth:

1. Regressing changes in yields on changes in yields, which is what we have done in this chapter. The formula for a change-on-change regression assuming a dependent variable y and independent variable x is as follows:

   $$ \Delta \text y_\text t=\alpha +\beta \Delta \text x_\text t+\Delta \epsilon_\text t $$

   where:

   $$ \begin{align*} \Delta \text y_\text t & =\text y_\text t-\text y_{\text t-1} \\ \Delta \text x_\text t & =\text x_\text t-\text x_{\text t-1} \\ \end{align*} $$

2. Regressing yields on yields, i.e., trying to establish a relationship between the yield on instrument x at time t and the yield on instrument y at time t.

   Mathematically,

   $$ \text y_\text t=\alpha + \beta \text x_\text t+\epsilon_\text t $$

Using either approach results in estimates that are unbiased and consistent. However, one of the most important assumptions of regression analysis is that the error terms are independent of each other, i.e., the error term at time t-1 is independent of the error term at time t. We also assume that the error terms are uncorrelated with the independent variable. In reality, however, the error terms are unlikely to be independent of each other; they are likely to be correlated over time. The consequence of this is that the estimated regression coefficients (in both level and change regression) are not efficient.

Illustration: Serial correlation

Let’s assume that \(\alpha = 0\), and \(\beta = 1\), y = yield on a coupon bond, and x = yield on another near maturity coupon bond. Let’s further assume that the following data has been observed:

$$ \begin{array}{c|c|c} {} & \textbf{Yield on bond yesterday} & \textbf{Yield on bond today} \\ \hline {x} & {10\%} & {10\%} \\ \hline {y} & {2\%} & {?} \\ \end{array} $$

Let’s try to predict the yield on y-bond today using the level (yields on yields) regression equation. It turns out that the predicted yield will be 10%, despite it being just 2% yesterday:

$$ \text y_\text t=0+1×10+\epsilon_\text t =10 $$

But there lies the problem: If the gap between today’s and yesterday’s yield was so big, with a realized error of −8%, then we would expect that the error today will not be far from −8%. Further, the yield of the y-bond yield will be closer to 2% than the 10% predicted by the level regression.

Bottom line: The errors are not likely to be independent of each other, as assumed, but rather correlated (persistent) over time. Generally, autocorrelation is frequently observed. Today’s estimate is not independent of yesterday’s.

Third Model

To recognize serial correlation among the error terms, there is a third way to model the relationship between two bond yields (assuming some constant correlation < 1):

$$ \epsilon_\text t=\rho \epsilon_{\text t-1}+ \text v_\text t $$

The model assumes that today’s error term consists of some part of yesterday’s error term, plus a new random fluctuation.

Let’s illustrate how this works using the example above. If \(\rho\) = 0.75, for example, then yesterday’s error of −8% would generate an average error of 75% × −8% or −6% today and, therefore, the expected y-bond yield would be 10% − 6% or 4%, a more realistic estimate.

Principal Component Analysis and Its Application to Construction of a Hedging Portfolio

Modern risk management is all about measuring the risk of large portfolios comprised of many positions that are exposed to a large number of risk factors. As the number of positions increases, so does the number (and complexity) of computations. The covariance matrix, for instance, has dimensions \(N^2\). A portfolio with 100 variables requires a matrix with 10,000 entries. In finance, this is known as the curse of dimension. The problem can be solved by employing principal component analysis.

Principal component analysis (PCA) is a mathematical procedure that transforms a number of correlated variables into a (smaller) number of uncorrelated variables called principal components. It attempts to explain all factor exposures using a small number of uncorrelated exposures that capture most of the risk.

To see how this works, we consider a set of swap rates from 1 to 30 years, at annual maturities. The PCA approach creates 30 interest rate factors or components, where each factor describes a change in each of the 30 rates. For example, one factor might be a simultaneous change of 10 basis points in the 1-year rate, 9.9 basis points in the 2-year rate, 9.8 basis points in the 3-year rate, and so forth. This diverges from regression analysis which looks at variances of rates and their pairwise correlations.

The 30 factors have the following properties:

1. The sum of the variances of the principal components equals the sum of the variances of the individual rates.
2. The PCs are not correlated with each other.
3. Each principal component is chosen to have the maximum possible variance, given the earlier principal components.

A huge plus for PCA is that out of the 30 PCs, we only really need to describe the volatility and structure of the first three. This is because the sum of the variances of the first three PCs provides a good approximation of the sum of the variances of all rates.

The Implication of PCA on Hedging

Given a large set of rates, we can conduct PCA and obtain information regarding how many rates, and which factors are needed to hedge k% of the variance in the rates. K can be any number but in practice, it is chosen to describe 90-98% of the variance of the dataset. Rather than work with a large set of rates, we are able to focus on a few key risk drivers to hedge our exposure, which is a much simpler approach.

Question

A trader at a large bank plans to short $100 million of the \(3\frac { 2 }{ 7 } \)s of February 20, 2019 and purchase some amount of the \(TIPS\) \(2\frac { 3 }{ 7 } \) s of January 20, 2019 against that assuming that the nominal yield in the data changes by 1.044 basis points per basis-point change in the real yield. The yields and \(DVO1\)s of a \(TIPS\) and a nominal US Treasury as of April 30, 2015 are provided as follows:

$$ \begin{array}{c|c|c|c|c} \textbf{Bond} & \textbf{DVO1} \\ \hline 2\frac { 3 }{ 7 } s \text{ of } \text{ January 20, } 2019 & 0.078 \\ \hline 3\frac { 2 }{ 7 } s \text{ of } \text{ February 20,} \ 2019 & 0.052 \\ \end{array} $$

Compute the \(TIPS\) face amount that should be purchased for the trade to be hedged against the interest rate levels.

1. $69.9 million.
2. $156.6 million.
3. $150 million.
4. $66.7 million.

The correct answer is A.

This can be achieved by making the trade \(DVO1\)-neutral.

The trader has to buy the \({ F }^{ R }\) face amount of the \(TIPS\) such that:

$$\begin{align*} { F }^{ R }\times \frac { 0.078 }{ 100 } &=$\text{100 million} \times \frac { 0.052 }{ 100 } \times 1.044\\ \Rightarrow { F }^{ R }&=$\text{69.6 million} \end{align*}$$