Rating Assignment Methodologies

p>

After completing this reading, you should be able to:

• Explain the key features of a good rating system.
• Describe the expert-based approaches, statistical-based models, and numerical approaches to predicting default.
• Describe a rating migration matrix and calculate the probability of default, the cumulative probability of default, marginal probability of default, and annualized default rate.
• Describe rating agencies’ assignment methodologies for issue and issuer ratings.
• Describe the relationship between borrower rating and the probability of default.
• Compare agencies’ ratings to internal experts-based rating systems.
• Distinguish between the structural approaches and the reduced-form approaches to predicting default.
• Apply the Merton model to calculate default probability and the distance to default and describe the limitations of using the Merton model.
• Describe linear discriminant analysis (LDA), define the Z-score and its usage, and apply LDA to classify a sample of firms by credit quality.
• Describe the application of a logistic regression model to estimate default probability.
• Define and interpret cluster analysis and principal component analysis.
• Describe the use of a cash flow simulation model in assigning rating and default probability and explain the limitations of the model.
• Describe the application of heuristic approaches, numeric approaches, and artificial neural networks in modeling default risk and define their strengths and weaknesses.
• Describe the role and management of qualitative information in assessing the probability of default.

Key Features of a Good Rating System

Ratings play an important role in the management of credit risk. Entities – both private and public – need favorable credit ratings to demonstrate their creditworthiness and strong financial standing. An entity’s credit rating is often one of the metrics regulators draw upon when determining capital provisions used to absorb unanticipated credit losses. But what’s the exact purpose of ratings?

A credit rating is a professional opinion regarding the creditworthiness of an entity or a given financial instrument, that is issued using a defined, well-structured ranking system of rating categories. Ratings are essential tools for measuring the probability of a default event occurring in a specific time horizon.

The credit crisis of the 1980’s served as a wake-up call to banks and strengthened the case for more hands-on credit risk assessment. According to data from the Federal Deposit Insurance Corporation, a total of 1,617 commercial and savings banks failed within the 14-year period between 1980 and 1994. The major reason behind these failures was poor credit analysis. The Depository Institutions Deregulation and Monetary Control Act of 1980 had loosened lending regulations, giving banks more lending powers. Banks rushed into speculative lending without paying attention to the creditworthiness of borrowers. In the aftermath of the crisis, banks improved loan review and loan risk-rating systems. Besides, they entrenched the use of credit ratings in their risk management programs.

As a general rule, ratings must be objective. As long as the same inputs are used and a similar methodology is adopted by different analysts, they should all yield similar ratings.

There are three main features of a good rating system:

1. Objectivity and Homogeneity

   • To be objective, the rating system must produce judgments that are solely tied to the credit risk profile of the issuer of a financial instrument.

   • To be homogeneous, ratings must be comparable among market segments, portfolios, and customer types.

2. Specificity

   • To be specific, the rating system must measure the distance from a default event without considering other corporate features, such as short-term fluctuations in stock price, that have no direct link to it.

3. Measurability and Verifiability

   • Ratings must provide correct expectations related to default probabilities which are backtested on a continuous basis.

Expert-based Approaches, Statistical-based Models, and Numerical Approaches to Predicting Default

Although a default event can bring about heavy losses, its probability of occurrence is usually very low. Even in the deepest ebbs of a recession, for example, the default rate has been found to be in the range of 2% to 5%. To come up with credible, reliable estimates of the default rate, an analyst has to balance knowledge with perception and intuition.

Over the years, the approaches below have been adopted by analysts to predict default.

Structured Expert-based Models

These are models developed by credit analysts and other industry experts by leveraging their knowledge and experience. They are essentially internal models developed by banks to assess the probability of default.

Expert-based models are premised upon economic theory regarding the framework of optimal corporate financial culture. These models take long to develop mainly because of lack of homogeneous reliable data.

Study on corporate financial structure began in the 1950’s. Modigliani and Miller kick-started the process when they developed a framework to establish corporate value and assess the relevance of a firm’s financial structure. Various other publications followed, with each trying to dissect the financial anatomy of institutions, with a particular emphasis on the probability of default. A notable model that’s credited with transformative insights on default is the Wilcox model.

Wilcox’s Model

Under this approach, we look at a model developed by Wilcox in 1971, built upon the famous Gambler’s ruin theory. Wilcox takes a cash flow approach to default. According to the model, a firm’s financial state can be defined as its adjusted cash position or net liquidation at any time. The time of bankruptcy is based on the inflows and outflows of liquid resources. The value of equity is a reserve, and cash flows either add to or drain from this reserve. If an entity depletes its reserve, it is declared bankrupt.

In the model, cash flows are either positive or negative and the reserve is the value of equity. Given cash flows, the probability default can be computed. The “distance to default” in this model is the sum of book equity and expected cash flow divided by the cash flow volatility.

Scott (1981) supports Wilcox’s view by arguing that if the current cash flows are able to predict the corporate financial position, then past and present cash flows should be able to determine and predict corporate default.

A good number of expert-based approaches are premised upon selected characteristics of the borrower. Most of these approaches are known by their acronyms. They include:

• The 4 C’s approach, which looks at Character, Capital, Coverage, and Collateral (proposed by Altman of New York University in various editions till the end of the 1990s).
• The CAMELS (J.P Morgan) approach, which looks at Capital adequacy, Asset quality, Management, Earnings, Liquidity, and Sensitivity
• The LAPS approach (Goldman Sachs valuation system), which looks at Liquidity, Activity, Profitability, and corporate structure.

Statistical-based Models

Statistical-based approaches to default prediction are built around the idea that every quantitative model used in finance is just a controlled description of real-world mechanics. In other words, quantitative models are used to express a viewpoint of how the world will likely behave given certain criteria.

Quantitative financial models embody a mixture of statistics, behavioral psychology, and numerical methods.

Every quantitative model has two components:

• The formal (quantitative) formulation that explains the simplified view of the world we are trying to catch.
• The assumptions made to build the model that set the foundation of relations among variables. In addition, there are boundaries of the validity and scope of application of the model.

A model’s assumptions should cover organizational behavior, possible economic events, and predictions on how market participants will react to these events.

The focus of statistical-based models is the assessment of default risk for unlisted firms. However, these models can be useful in assessing default risk for large corporations, financial institutions, special purpose vehicles, government agencies, non-profit organizations, small businesses, and consumers.

Numerical Approaches

Numerical approaches are built around the concept of machine learning. These models assume that it is possible to gather data from the environment and then train an algorithm to make informed conclusions using such data.

Rating Migration Matrix

A rating migration matrix gives the probability of a firm ending up in a certain rating category at some point in the future, given a specific starting point. The matrix, which is basically a table, uses historical data to show exactly how bonds that begin, say, a 5-year period with an Aa rating, change their rating status from one year to the next. Most matrices show one-year transition probabilities.

Transition matrices demonstrate that the higher the credit rating, the lower the probability of default.

The table below presents an example of a rating transition matrix according to S&P’s rating categories:

$$ \textbf{One-year transition matrix}$$

$$ \small{\begin{array}{l|cccccccc} \textbf{Initial}& {} & \textbf{Rating} & \textbf{at} & \textbf{year} & \textbf{end} & {} & {} & {} \\ \textbf{Rating} & \textbf{AAA} & \textbf{AA} & \textbf{A} & \textbf{BBB} & \textbf{BB} & \textbf{B} & \textbf{CCC} & \textbf{Default}\\ \hline \text{AAA} & {90.81\%} & {8.33\%} & {0.68\%} & {0.06\%} & {0.12\%} & {0.00\%} & {0.00\%} & {0.00\%} \\ \text{AA} & {0.70\%} & {90.65\%} & {7.79\%} & {0.64\%} & {0.06\%} & {0.14\%} & {0.02\%} & {0.00\%} \\ \text{A} & {0.09\%} & {2.27\%} & {91.05\%} & {5.52\%} & {0.74\%} & {0.26\%} & {0.01\%} & {0.06\%} \\ \text{BBB} & {0.02\%} & {0.33\%} & {5.95\%} & {86.93\%} & {5.30\%} & {1.17\%} & {0.12\%} & {0.18\%} \\ \text{BB} & {0.03\%} & {0.14\%} & {0.67\%} & {7.73\%} & {80.53\%} & {8.84\%} & {1.00\%} & {1.06\%} \\ \text{B} & {0.00\%} & {0.11\%} & {0.24\%} & {0.43\%} & {6.48\%} & {83.46\%} & {4.07\%} & {5.20\%} \\ \text{CCC} & {0.22\%} & {0.00\%} & {0.22\%} & {1.30\%} & {2.38\%} & {11.24\%} & {64.86\%} & {19.79\%} \\ \end{array}}$$

Exam Tips:

• Each row corresponds to an initial rating.
• Each column corresponds to a rating at the end of 1 year. For example, a bond initially rated BB has an 8.84% chance of moving to a B rating by the end of the year.
• You will need to recall the rules of probability from mathematics to come up with n-year transition probabilities, where n > 1
• The sum of the probabilities of all possible destinations, given an initial rating, is equal to 1 (100%).
• Credit ratings are their most stable over a one-year horizon. Stability decreases with longer horizons.

Key Measures Used to Assess the Risk of Default

To come up with various measures of default risk, a pool of issuers, called a cohort, is formed on the basis of the rating held on a given calendar date. The default or survival status of the members of the cohort is then tracked over some stated time horizon. The time horizon K for which we desire to measure a default rate is divided into evenly spaced time intervals (e.g. months, years) of length k.

Probability of Default

This measures the likelihood of default over a single time period of length k. It is simply the fraction of the cohort that survives to the end of the period:

$$ \begin{align*} \text{ PD }_\text{ k }=\frac { \text{defaulted}_\text{ k }^\text{ t+k } }{ \text{cohort}_\text{ t } } \end{align*}$$

Where:

\(\text{ PD }_{\text{ k }}\)= Probability of default.

\(\text{defaulted}_\text{ k }^\text{ t+k }\)= Number of issuer names (members of the cohort) that have defaulted between time \(\text{t}\) and time \(\text{t+k}\).

Cumulative Probability of Default

The K-horizon cumulative default rate is defined as the probability of default from the time of cohort formation up to and including time horizon K $$ \begin{align*} \text{ PD }_\text{ k }^\text{ cumulative }=\frac { \sum _{ \text i=\text t }^{\text i=\text{t}+\text{k} }{ \text{ defaulted }_\text{ i } } }{\text{ cohort}_\text{ t } } \end{align*}$$. If K is 5 years, for example, the cumulative probability of default in year 5 means the probability of an issuer name defaulting in either year 1, 2, 3, 4 or 5 (i.e., the sum of defaults in years 1, 2, 3, 4, and 5).

The following table gives the cumulative default rates provided by Moody’s.

$$ \textbf{Cumulative Ave Default Rates (%) (1970-2009, Moody’s)} $$

$$ \begin{array}{c|c|c|c|c|c|c|c} \textbf{ } & \textbf{1} & \textbf{2} & \textbf{3} & \textbf{4} & \textbf{5} & \textbf{7} & \textbf{10} \\ \hline \text{ Aaa} & {0.000} & {0.012} & {0.012} & {0.037} & {0.105} & {0.245} & {0.497} \\ \hline \text{ Aa} & {0.022} & {0.059} & {0.091} & {0.159} & {0.234} & {0.348} & {0.542} \\ \hline \text{A } & {0.051} & {0.165} & {0.341} & {0.520} & {0.717} & {1.179} & {2.046} \\ \hline \text{ Baa} & {0.176} & {0.494} & {0.912} & {1.404} & {1.926} & {2.996} & {4.551}\\ \hline \text{ Ba} & {1.166} & {3.186} & {5.583} & {8.123} & {10.397} & {14.318} & {19.964} \\ \hline \text{ B} & {4.546} & {10.426} & {16.188} & {21.256} & {25.895} & {34.473} & {44.377} \\ \hline \text{ Caa-C} & {17.723} & {29.384} & {38.682} & {46.094} & {52.286} & {59.771} & {71.376} \\ \end{array} $$

According to the table, an issuer name with an initial credit rating of Ba has a probability of 1.166% of defaulting by the end of the first year, 3.186% by the end of the second year, and so on. We can interpret the other default rates in a similar manner.

Marginal Probability of Default

The marginal default rate is the probability that an issuer name that has survived in a cohort up to the beginning of a particular interval k will default by the end of the time interval.

$$ \begin{align*} \text{ PD }_\text{ k }^\text{ marginal }=\text{ PD }_\text{ t+k }^\text{ cumulative }-\text{ PD }_\text{ k }^\text{ cumulative } \end{align*}$$

Annualized Default Rate

For discrete intervals, the annualized default rate can be computed as follows:

$$ \begin{align*} \text{ ADR }_\text{ t }=1-\sqrt [ \text{t} ]{ \left( 1-\text{ PD }_\text{ t }^\text{ cumulative } \right) } \end{align*}$$

For continuous intervals,

$$ \begin{align*} \text{ ADR }_\text{ t }=-\frac { \text{ln}\left( 1-\text{ PD }_\text{ t }^\text{ cumulative } \right) }{ \text{t} } \end{align*}$$

Rating Agencies’ Assignment Methodologies for Issue and Issuer Ratings

To come up with a credible and reliable issue or issuer credit ratings, rating agencies run systematic surveys on all default determinants. The process usually combines both subjective judgments and quantitative analysis.

Rating agencies earn the largest percentage of their revenue in the form of counterparty fees. A small proportion comes from selling information to market participants and investors. Due to the need to nurture and maintain a good reputation, rating agencies endeavor to offer accurate results that the investment community can rely upon.

To successfully assign a rating, an agency must have access to objective, independent, and sufficient insider information. This means that the rating agency can access privileged information that’s not in the public domain. However, most agencies have a well-structured process that is followed, culminating in the issuance of a credit rating. Standard & Poor’s, for example, sets out an eight-step process:

1. A rating request is received from the issuer.
2. The agency conducts preliminary evaluation of the issuer.
3. The agency’s representatives meet with the issuer’s management.
4. The agency gathers all the relevant information and analyzes the issuer in detail.
5. The rating committee reviews the analysis results and votes on the recommendations.
6. The issuer is notified of the results of the process.
7. The agency’s rating opinion is published.
8. The agency continuously monitors the issuer/issue.

Although a wide range of information is taken into account while evaluating an issue/issuer, rating agencies put more weight on the two analytical areas highlighted below.

Evaluation of Financial Risks

This involves scrutinizing the issuer’s financial statements to assess issues such as accounting methods, income generation capacity, movement of cash, and the capital structure. Standard & Poor’s for example, focuses on coverage ratios, liquidity ratios, and profitability ratios.

Evaluation of Business Risks

This involves industry analysis, peer comparative analysis, and assessment of country risk as well as the issuer’s position relative to peers.

Some of the other action points include:

• Assessment of firm strategy, coherence, and consistency.
• Assessment of the management’s reputation and experience.
• Establishment of how diverse the issuer’s profit and cash flows are.
• Assessment of the issuer’s competitive edge.
• Assessment of the resilience of the business to business uncertainty and volatility.

In addition, the issuer’s internal governance and control systems are equally critical components of credit analysis.

Currently, there are three major rating agencies: Moody’s, Standard & Poor’s (S&P), and Fitch. While Moody’s focuses on issues, S&P focuses on issuers. Fitch is the smallest of the three and covers a more limited share of the market. It positions itself as a “tie-breaker” when the other two agencies have similar ratings that are, however, not equal in scale.

The Relationship between Borrower Rating and Probability of Default

A borrower’s credit rating reflects their probability of default. The higher the rating, the more financially reliable a borrower is considered to be. This implies that higher-rated issues have a lower probability of default. In fact, the highest-rated issues almost never default even over a significant period of, say, 10 years. The lowest-rated issues, on the other hand, often default early and are almost assured of default after a 10-year period.

Agencies’ Ratings vs. Internal Expert-based Rating Systems

Banks’ internal classification methods are somewhat different from agencies’ ratings assignment processes. Nevertheless, sometimes their underlying processes are analogous; when banks adopt judgmental approaches to credit quality assessment, the data considered and the analytical processes are similar.

An expert-based approach relying on judgment will require significant experience and repetitions in order for many judgments to converge. In other words, judgment-based schemes need long-lasting experience and repetitions, under a constant and consolidated method, to assure the convergence of judgments. As we would expect, therefore, internal rating systems take time to develop. The failure to attain consistency under the expert-based approach can be attributed to several factors, some of which are outlined below:

• Organizational patterns are intrinsically dynamic.
• There’s the issue of mergers and acquisitions that blend different credit portfolios, credit approval procedures, internal credit underwriting powers, and so forth.
• Over time, company culture changes, and so do experts’ skills and analytical frameworks, particularly with reference to qualitative information.

However, there is no proven inferiority or superiority of expert-based approaches versus formal ones, based on quantitative analysis such as statistical models.

Earlier on we looked at the qualities of a good rating system – objectivity and homogeneity, specificity, measurability, and verifiability. We can compare agencies’ ratings and internal expert-based rating systems along similar lines:

• On objectivity and homogeneity, agencies’ ratings are 73% compliant, while internal expert-based rating systems are 30% compliant.
• On specificity, agencies’ ratings are close to 100% compliant, while internal expert-based rating systems are 75% compliant.
• On measurability and verifiability, agencies’ ratings are 75% compliant, while internal expert-based rating systems are 25% compliant.

$$ \begin{array}{c|cc} \textbf{Quality} & \textbf{Compliance level} & {} \\ \hline \text{} & \text{Agencies’} & \text{Internal experts-} \\ {} & \text{ratings} & \text{based ratings} \\ \hline \text{Objectivity and Homogeneity} & {73\%} & {30\%} \\ \hline \text{Specificity} & {100\%} & {75\%} \\ \hline \text{Measurability and Verifiability} & {75\%} & {25\%} \\ \end{array} $$

Structural Approaches vs. Reduced-form Approaches to Predicting Default

Historically, we can identify two distinctive approaches for modeling credit risk – structural approaches and reduced-form approaches.

Structural approaches rely on economic and financial theoretical assumptions to describe the path to default. Explicit assumptions are made over aspects such as the capital structure and the evolution of a firm’s assets and liabilities. Notably, structural models assume that the modeler has the same information set as the firm’s manager – complete knowledge of all the firm’s assets and liabilities. The default event (which is endogenous) is then determined as the time when the assets are below some specified level. The model is built to estimate the formal relationships that associate with the relevant variables.

The assumption that the modeler has the same information set as the firm manager has an inherent drawback in the sense that the default time is predictable. This leads to a situation where investors demand unrealistic credit spreads (i.e. excess yield) to bear the default risk of the issuer. A good example of a structural approach is the Merton model.

Reduced-form models, in contrast, arrive at a final solution using the set of variables that is the most statistically suitable without considering any theoretical or conceptual causal relationships among variables. In other words, the precise mechanism that triggers a default event is left unspecified and viewed as a random point process. In essence, reduced-form models view defaults as some kind of a “black box” whose occurrence cannot be predicted.

There are two reasons reduced-form models may be favored at the expense of structural models:

• The assumption that the modeler has the same information set as the risk manager is unrealistic. The risk manager usually has access to information that might not be publicly available.
• Structural models may not accurately describe the economics of the default mechanism. There is actually evidence in support of this, and we only need to look at famous bankruptcy episodes that were not preceded by obvious warning signs, such as Bear Sterns, LTCM, and Northern Rock.

Applying the Merton Model to Calculate Default Probability and the Distance to Default

The Merton model, which is an example of a structural approach, is based on the premise that default happens when the value of a company’s asset falls below the “default point” (value of the debt).

The model views a company’s equity as a European call option on the underlying value of the company with a strike price equal to the face value of the company’s debt. As such, the value of equity is a by-product of the market value and volatility of assets, as well as the book value of liabilities. However, the model recognizes that firm value and volatility cannot be observed directly. Both of these values can be subtracted from equity value, the volatility of equity, and other observable variables by solving two nonlinear simultaneous equations. Once these values have been calculated, the probability of default is determined as the normal cumulative density function of a Z-score based on the underlying value of the company, volatility of the company, and the face value of the company’s debt.

Model assumptions:

• The entity has homogeneous debt maturing at time T.
• The entity’s capital structure is composed of debt and equity.
• There are no coupons, dividends, and penalties for short sales.
• Assets follow geometric Brownian motion.

Probability of Default – PD

$$ \begin{align*} \text{PD}=\text{N}\frac { \left[ \text{ln}\left( \text{F} \right) -\text{ln}\left( \text{V}_\text{A} \right) -\mu \text{T}+\frac { 1 }{ 2 } { \sigma }_\text{A}^{2}T \right] }{ { \sigma }_\text{A}\sqrt { \text{T}} } \end{align*}$$ Where:

\(\text{ln}\) = The natural logarithm.

\(\text{F}\) = Debt face value.

\(\text{ V }_\text{ A }\)= Firm asset value.

\(\mu\)= Expected return in the “risky world”.

\(\text{T}\) = Time remaining to maturity.

\({ \sigma }_\text{ A }\) =Volatility (standard deviation of asset values).

\(\text{N}\)= Cumulated normal distribution operator.

Distance to default

This is the distance between the expected value of an asset and the default point. Assuming T = 1,

$$ \begin{align*} \text{DtD}=\frac { \text{ln}\left( \text{V}_\text{A} \right) -\text{ln}\left( \text F \right) +\left( \mu_{\text{risky}}-\frac { 1 }{ 2 } { \sigma }_\text{A}^{ 2 }\text{T} \right) -\text{“other payouts”} }{ { \sigma }_\text{A} } \cong \frac { \text{lnV}-\text{lnF} }{ { \sigma }_\text{A} } \end{align*}$$ 

If the assumptions of the Merton model really hold, the KMV-Merton model should give very accurate default forecasts. However, the model is criticized due to the following reasons:

• It requires some subjective estimation of the input parameters.
• It is difficult to construct theoretical distance to default without the assumption of the normality of asset returns.
• It does not distinguish among different types of long-term bonds according to their seniority, collateral, covenants, or convertibility.

Linear Discriminant Analysis

A scoring model is a model in which various variables are weighted in varying ways and result in a score. This score subsequently forms the basis for a decision. In finance, scoring models combine quantitative and qualitative empirical data to determine the appropriate parameters for predicting default. Linear discriminant analysis (LDA) is a popular statistical method of developing scoring models.

The linear discriminant analysis classifies objects into one or more groups based on a set of descriptive features. Models based on LDA are reduced-form models due to their dependency on exogenous variable selection, default composition, and the default definition. The variables used in an LDA model are chosen based on their estimated contribution (i.e., weight) to the likelihood of default. These variables are both qualitative and quantitative. Examples are the skill and experience of management and the liquidity ratio, respectively. The contributions of each variable are added to form an overall score, called Altman’s Z-score.

Altman Z-score is essentially a bankruptcy prediction tool published by Edward I. Altman in 1968. Mr. Altman worked with 5 ratios: net working capital to total assets ratio, earnings before interest and taxes to total assets ratio, retained earnings to total assets ratio, market value of equity to total liabilities ratio, and finally, sales to assets ratio. Below is the LDA model proposed by Altman:

$$ \begin{align*} \text{Z}=1.21 \text{x}_{ 1 }+1.4 \text{x}_{ 2 }+3.3 \text{x}_{ 3 }+0.6 \text{x}_{ 4 }+0.999 \text{x}_{ 5 } \end{align*}$$

where:

\(\text{x}_{ 1 }=\text{Working capital}/\text{total assets}\).

\(\text{x}_{ 2 }=\text{Retained earnings}/\text{total assets}\).

\(\text{x}_{ 3 }=\text{EBIT}/\text{total assets}\).

\(\text{x}_{ 4 }=\text{Equity market value}/\text{face value of term debt}\).

\(\text{x}_{ 5 }=\text{Sales}/\text{total assets}\).

In this model, the higher the Z-score, the more likely it is that a firm will be classified in the group of solvent firms. Altman worked with a Z-score range from -5.0 to +20.0, although higher scores may occur if a company has a high equity value and/or low level of liabilities.

A Z-score cutoff, also known as the discriminant threshold, is used to categorize firms into two groups: solvent firms and insolvent firms. Altman set the Z-score cutoff at Z = 2.675. Firms with a score below 2.675 are categorized as insolvent while those with a score above 2.675 are categorized as solvent.

Estimating Default using Logistic Regression Models

Logistic regression models (commonly referred to as LOGIT models) are a group of statistical tools used to predict default. They are based on the analysis of dependency among variables. They belong to the family of Generalized Linear Models (GLMs) used to analyze dependence, on average, of one or more dependent variables from one or more independent variables.

GLMs have three components:

• A Random Component: Identifies the target variable and its probability function.
• A Systematic Component: Specifies explanatory variables used in a linear predictor function.
• A Link Function: A function of the mean of the target variable that the model equates to the systematic component.

These three elements characterize linear regression models and are particularly useful when default risk is modeled.

Assume that p represents the probability that a default event takes place,which we denote as \(\text p =\text P\left( \text{Y}=1 \right) .\). Furthermore, let’s assume that we have two predictors \(-\text{x}_{ 1 } \text{ and } \text{x}_{ 2}\). We further assume a linear relationship between the predictor variables, and the LOGIT (log-odds) of the event that \(\text{Y} = 1\). This linear relationship can be written in the following mathematical form:

$$ \begin{align*} \text{LOGIT}\left( \text p \right) =\text{ln}\frac { \text p }{ 1-\text p } ={ \beta }_{ 0 }+{ \beta }_{ 1 }\text{x}_{ 1 }+{ \beta }_{ 2 }\text{x}_{ 2 }\dots \dots \dots \text{equation}\left(\text{I} \right) \end{align*}$$

The ratio \({ \text p }/{ 1-\text p }\) is known as the odds, i.e., the ratio between the default probability and the probability that a firm continues to be a performing borrower. The LOGIT function associates the expected value for the dependent variable to the linear combination of independent variables.

We can recover the odds by exponentiating the LOGIT function:

$$ \begin{align*} \frac { \text p }{ 1-\text p } ={ e }^{ { \beta }_{ 0 }+{ \beta }_{ 1 }\text{x}_{ 1 }+{ \beta }_{ 2 }\text{x}_{ 2 } } \end{align*}$$

By simple algebraic manipulation, the probability of Y = 1, i.e., probability of default is:

$$ \begin{align*} \text p &=\frac { { e }^{ { \beta }_{ 0 }+{ \beta }_{ 1 }\text{x}_{ 1 }+{ \beta }_{ 2 }\text{x}_{ 2 } } }{ 1+{ e }^{ { \beta }_{ 0 }+{ \beta }_{ 1 }\text{x}_{ 1 }+{ \beta }_{ 2 }\text{x}_{ 2 } } }\\& =\frac { 1 }{ 1+{ e }^{ -\left( { \beta }_{ 0 }+{ \beta }_{ 1 }\text{x}_{ 1 }+{ \beta }_{ 2 }\text{x}_{ 2 } \right) } } \end{align*}$$

This formula shows that given some values of the parameters \({ \beta }_{ 1 }\) and \({ \beta }_{ 2 }\), we can easily compute the LOGIT that Y = 1 for a given observation, or the probability Y = 1 (implying default).

Sources of information for the independent variables in statistical models include financial statements for a firm, external behavioral information (legal disputes, credit bureau reports, dun letters, etc.), and assessments covering factors such as management quality, the competitiveness of the firm, and supplier/customer relations.

Cluster Analysis

Statistical approaches such as LDA and LOGIT methods are called ‘supervised’ because a dependent variable is defined (the default) and other independent variables are used to work out a reliable solution to give an ex-ante prediction. However, we have some statistical techniques that do not define the independent variable. Such a technique is said to be unsupervised.

In unsupervised techniques, all the relevant borrower variables are reduced through simplifications and associations, in an optimal way, in order to end up with fewer but highly informative variables. It is noteworthy that the main aim of unsupervised techniques is not to predict the probability of default. Rather, they are used to simplify available information, paving way for more precise analysis. A good example of unsupervised techniques is cluster analysis.

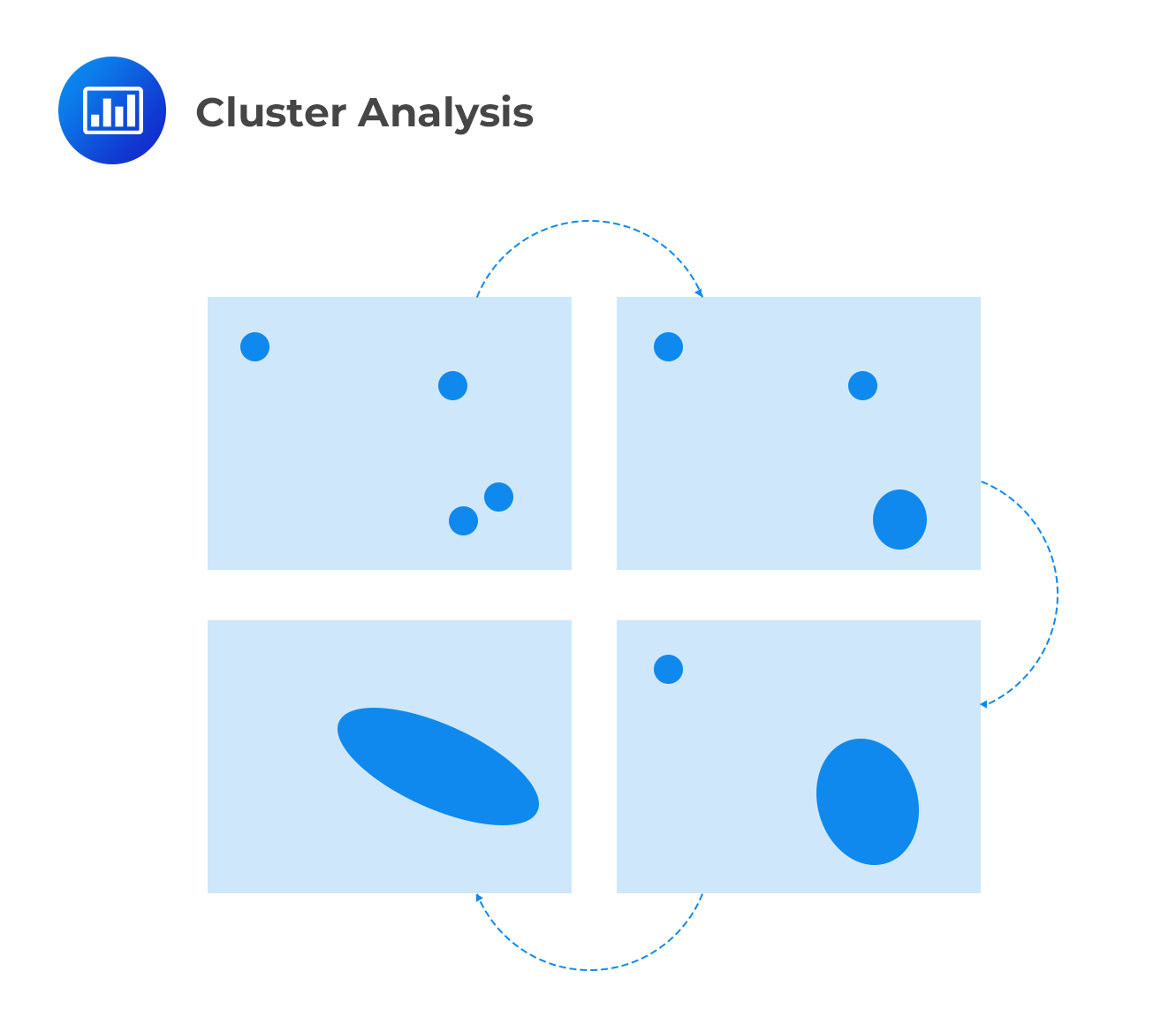
Cluster analysis, also called classification analysis, is a technique used to categorize objects or cases into relative groups called clusters. Groups represent observation subsets that exhibit homogeneity (i.e., similarities). In cluster analysis, there is no prior information about a group or cluster membership for any of the objects. Outside risk management parlance, cluster analysis is widely used. For example, it helps marketers discover distinct groups in their customer bases, and then use this knowledge to develop targeted marketing programs.

For risk managers keen to study the default profiles of borrowers, cluster analysis is very useful. Usually, a risk manager will have gathered borrower information and summarized it in columns and rows. Cluster analysis aims to single out bits of homogeneous information from the profiles of borrowers in order to establish a homogenous segment of borrowers whose empirical default rate can be calculated. The borrowers in each segment are broadly similar to one another. There are two forms of cluster analysis: hierarchical clustering and divisive/partitioned clustering.

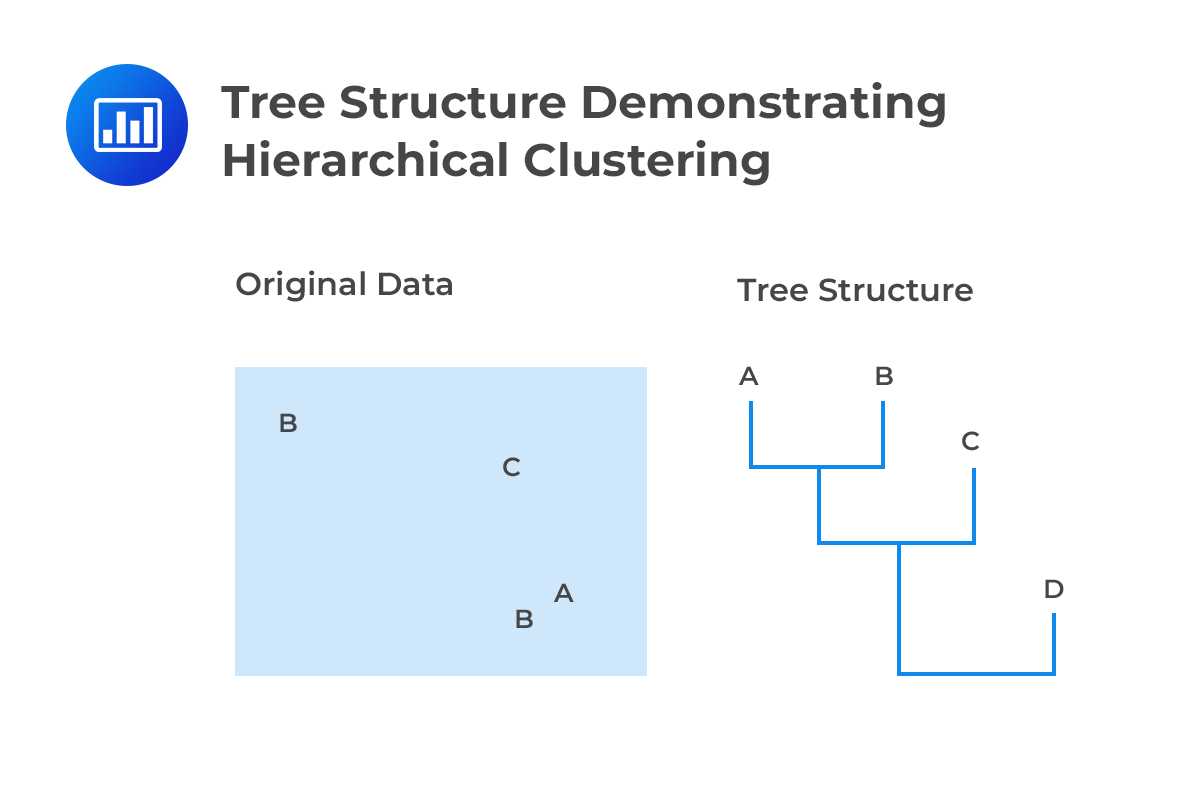
In hierarchical clustering, each observation is initially treated as a separate cluster. From this point, the algorithm repeatedly identifies the two clusters that are closest to each other. These clusters are then merged. This continues until all the clusters are merged together. This is illustrated below:

In the end, a risk manager ends up with data sorted in a tree structure with the clusters shown as leaves and the whole population shown as the roots. Therefore, the end result of the analysis gives:

• A small number of highly homogeneous, large clusters.
• Some small clusters with comprehensible and well-defined specificities.
• Single, very specific, nonaggregated units.

Hierarchical clustering has many applications. For example, it helps to detect anomalies in data. In the real world, many borrowers are outliers, (i.e., they have unique characteristics). A bank’s credit portfolio will often include start-ups, companies in liquidation procedures, and companies that have just merged or demerged, which may have very different characteristics from other borrowers. Cluster analysis offers a way to objectively identify these cases and to manage them separately from the remaining observations.

Divisive or partitioned clustering is the inverse of hierarchical clustering. Initially, all objects are considered a single large cluster. At each step of the iteration, the most heterogeneous cluster is divided into two. The process is iterated until all objects are in their own cluster.

Cluster analysis is widely used in finance. For example, firm profitability is a performance tool that’s apparent at the conceptual level but, in reality, is only a composite measure (ROS, ROI, ROE, and so forth). In spite of this, we still use the profitability concept as a means to describe the probability of default; so we need good measures, possibly only one. To reach this objective, we have to identify some aspects of a firm’s financial profile and also define how many ‘latent variables’ are behind the ratio system.

Component Analysis

Principal component analysis (PCA) is a mathematical procedure that transforms a number of correlated variables into a (smaller) number of uncorrelated variables called principal components. It attempts to explain all factor exposures using a small number of uncorrelated exposures that capture most of the risk.

In the context of credit risk assessment, there are several variables that collectively contribute to the probability of default. Therefore, the trick is to extract the variables that have maximum “power” over the default event.

The performance of a given variable (equal to the variance explained divided by the total original variance) is referred to as communality. Variables with higher communality have more ability to summarize an original set of variables into a new composed variable.

The starting point is the extraction of the first component (variable) that achieves maximum communality. The second extraction then focuses on the residuals not explained by the first component. This process is repeated until a new set of principal components has been created, which will be statistically independent and “explain” the default probability in descending order.

The Cash Flow Simulation Model

The cash flow simulation model seeks to come up with reliable forecasts of a firm’s Pro-forma financial reports in order to assess the probability of default. The model executes a large number of iterative simulations all of which represent possible future financial scenarios. Provided there’s a clear definition as to what constitutes a default event, the probability of default can be determined. The number of future scenarios in which default occurs, compared to the number of total scenarios simulated, can be assumed as a measure of default probability.

Cash flow simulation models are particularly useful when evaluating:

• Startups that have no historical data.
• Special purpose entities with a unique financial structure.
• Recently merged entities.

When working with cash flow simulation models, there are certain specifications that must be made regarding future pro-forma financial reports. These include:

• How much cash flows (a) will be generated by operations, (b) will be used for financial obligations and other investments, and (c) what are their determinants (demand, costs, technology, and other crucial hypotheses).
• Complete future Pro-forma specifications useful for supporting more traditional analysis by ratios as well as for setting covenants and controls on specific balance sheet items.

To determine the probability of default, there are two possible methods:

• Numerical simulation method: A large number of model iterations are used to describe different scenarios. These scenarios can be categorized as default, no-default, near-to-default, or stressed. The frequency of each type of scenario is then computed.
• Scenario approach: Probabilities are applied to discrete predefined scenarios. Ratings are then determined using weighted averages of future outcomes.

Most financial transactions involving credit come with restrictions that a borrower agrees to. These restrictions are set by the lending institution. For example, a lender can specify the maximum additional debt that the borrower can assume. A borrower can also be prevented from pledging certain assets if doing so would jeopardize a lender’s security. When using the cash flow simulation model, such covenants and negative pledges play a critical role. These contractual clauses have to be modeled and contingently assessed to verify both when they are triggered and what their effectiveness is.

Key Considerations When Using the Cash Flow Simulation Model

Model Risk

A key consideration when defining default is the model risk which stems from the fact that any model serves as a simplified version of reality, and it is difficult to tell if and when a default will actually be filed in real-life circumstances. It follows, therefore, that the default threshold needs to be specified such that it is not too early and not too late. If it is too early, there will be many potential defaults, resulting in transactions that are deemed risky when they are not truly risky. If it is too late, there will be very few potential defaults, resulting in transactions that are deemed less risky than they actually are.

Model Costs

A cash flow simulation model is very often either company-specific or industry-specific to reflect the prevalent unique circumstances. These models are often built and put into use under the supervision of a firm’s management and a competent, experienced analyst. The management has to mobilize resources to continually review and update the model. Trying to avoid these costs could reduce the model’s efficiency and accuracy over time.

Cash flow simulation models have their problems, particularly in form of model risk and costs. However, they remain the go-to tools when modeling default probability when historical data cannot be observed. There are not many feasible alternatives.

The Application of Heuristic Approaches, Numeric Approaches, and Artificial Neural Networks in Modeling Default Risk

Heuristic Approaches

In very general terms, a heuristic technique is any approach to problem-solving, learning, or discovery that employs a practical method not guaranteed to be optimal or perfect, but sufficient for the immediate goals. It is essentially a rule-of-thumb approach that endeavors to produce a “good enough” solution to a problem, in a reasonable timeframe.

A heuristic approach to modeling default risk is, by extension, a trial and error approach that mimics human decision-making procedures to generate solutions to problems in a time-efficient manner. In this approach, there’s no statistical modeling, and the goal is to reproduce decisions at the highest level of quality at a low cost. Heuristic approaches are also known as “expert systems” based on artificial intelligence techniques.

When using heuristic approaches to model default risk, there is no guarantee that the resulting probabilities will be the most accurate. Instead, these probabilities are considered good enough, and the path to their generation is faster and more cost-efficient.

Numeric Approaches

Unlike heuristic approaches, numerical approaches are geared toward reaching an optimal solution. “Trained” algorithms are used to make decisions in highly complex environments characterized by inefficient, redundant, and fuzzy information. A good example of these approaches would be neutral networks that are able to continuously auto-update themselves in order to adjust to environmental modifications.

Expert Systems

Expert systems are software solutions that attempt to provide answers to problems where human experts would otherwise be needed. Expert systems are part of traditional applications of artificial intelligence.

For a human to become an expert in a certain field, they have to gather knowledge through learning and research and subsequently come up with an organized way to apply the knowledge in problem-solving. Expert systems work in a similar manner, where they create a knowledge base and then use knowledge engineering to codify the knowledge into a framework.

Expert systems have four components:

1. The knowledge base is essentially a database of facts, measures, and rules that have been established following successful tackling of problems in the past.
2. The ‘working memory’ (also known as short-term memory) contains information on the problem to be solved. In other words, the working memory is the virtual space in which rules are combined and where final solutions are produced.
3. The ‘inferential engine’ serves as the brain of the expert system. The inference engine contains rules to solve a specific problem. It refers to the knowledge from the Knowledge Base. When presented with a problem, the inference engine selects facts and rules to apply in an attempt to answer the user’s query
4. The users’ interface helps the user to communicate with the system. The interface takes the user’s query in a readable form and passes it to the inference engine. Once the problem is worked out, the interface displays the results to the user.

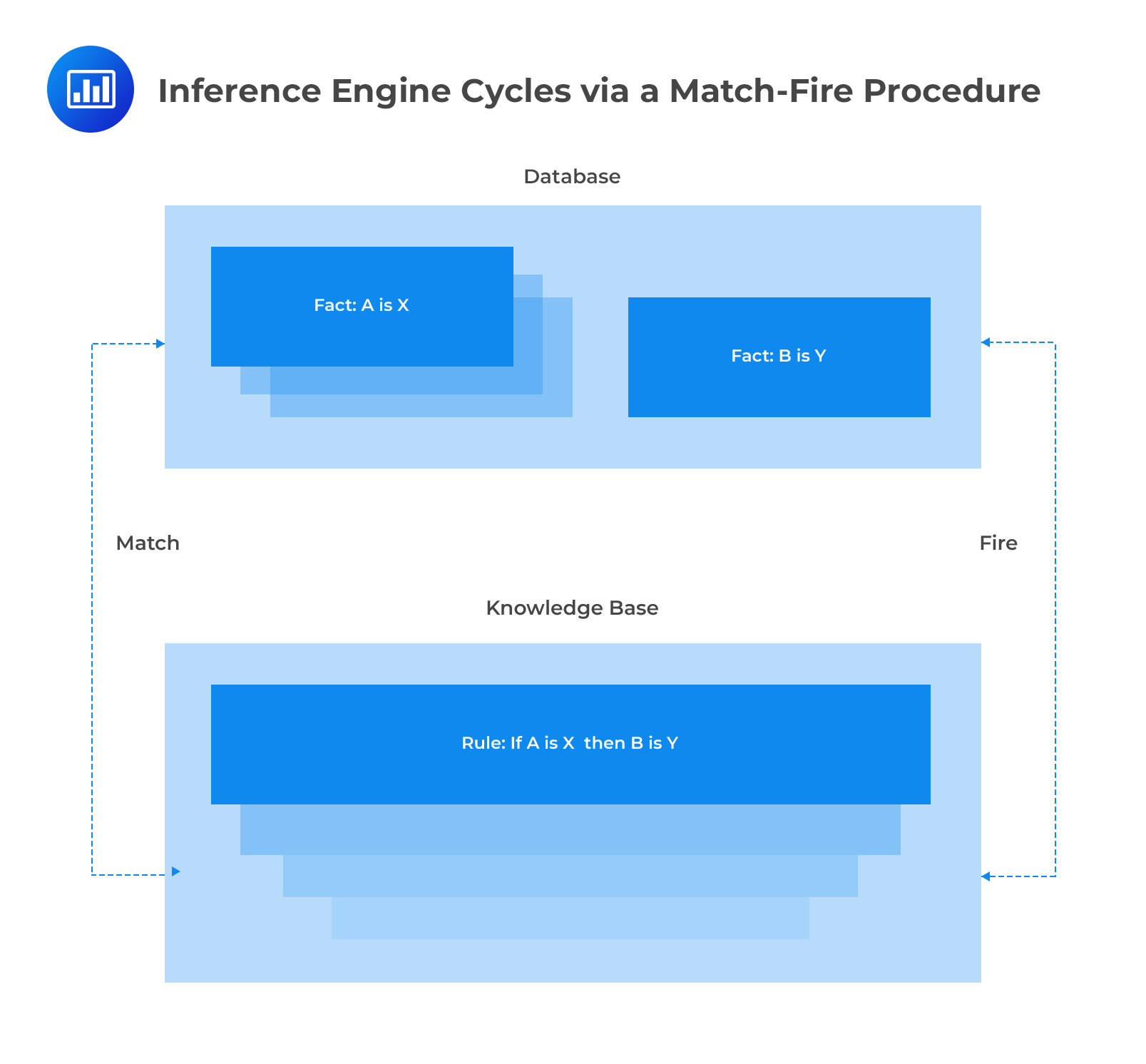
The knowledge base of an expert system consists of many inference rules which are designed to resemble human behavior. Rules are basically a set of IF-THEN statements. The inference engine compares each rule stored in the knowledge base with facts contained in the database. When the IF part of the rule matches a fact, the rule is fired and it’s THEN part is executed. The matching of the IF part of a rule to the facts generates inference chains. The inference chains indicate how an expert system applies the rules to reach a conclusion.

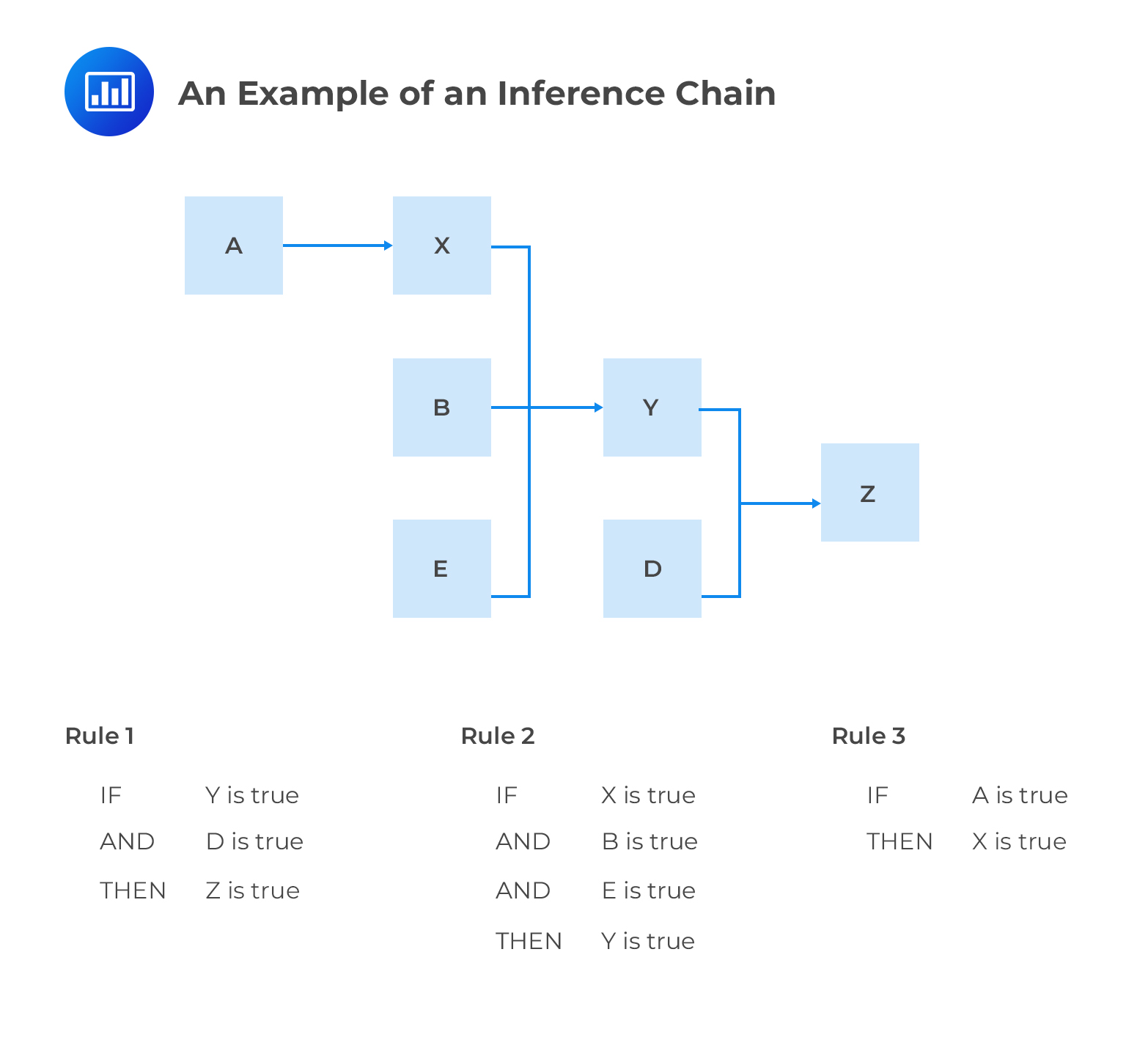The inference engine uses either backward chaining or forward chaining. With backward chaining (also known as goal-driven reasoning), the system’s starting point is a list of goals. Working backward, the system looks to find paths that will allow it to achieve these goals. The system looks through the rules until one which best aligns to the desired goal is found. With forward chaining (also known as data-driven reasoning), the reasoning starts from the known data and proceeds forward with that data. Inference rules are applied until the desired goal is achieved. Once the path is recognized as successful, it is applied to the data. Therefore, the forward chaining inference engine is appropriate in situations where we have gathered some information and wish to infer whatever can be inferred from it. The backward chaining inference engine is appropriate if we begin with a hypothetical solution to a problem and then attempt to find facts to prove it.

Expert systems may also include fuzzy logic applications. Fuzzy logic is derived from ‘fuzzy set theory’, which is able to deal with approximate rather than precise reasoning. In other words, the system works with “degrees of truth” rather than the usual “true or false” (1 and 0) Boolean logic on which most modern computer systems are based. In fuzzy logic, 0 and 1 are considered “extreme” cases of truth, but the system also includes the various states of truth in between. For example, when assessing the solvency of a firm, we would normally work with two states – solvent and insolvent. With fuzzy logic application, we might, in addition, consider a range of other states in between. A firm can be declared “0.75 solvent.”

Fuzzy logic is applied in default risk analysis because many rules related to default are simply ‘rule-of-thumb’ that have been derived from experts’ own feelings. Often, thresholds are set for ratios but, because of the complexity of real-world, they can turn out to be both sharp and severe in many circumstances. Therefore, it is necessary to work with a range of values.

Artificial Neural Networks (ANN)

Artificial neural networks are trainable algorithms that simulate the behavior and working of the human brain. They are able to self-train and gain the ability to organize and formalize unclassified information. Most importantly, neural networks are able to make forecasts based on the available historical information.

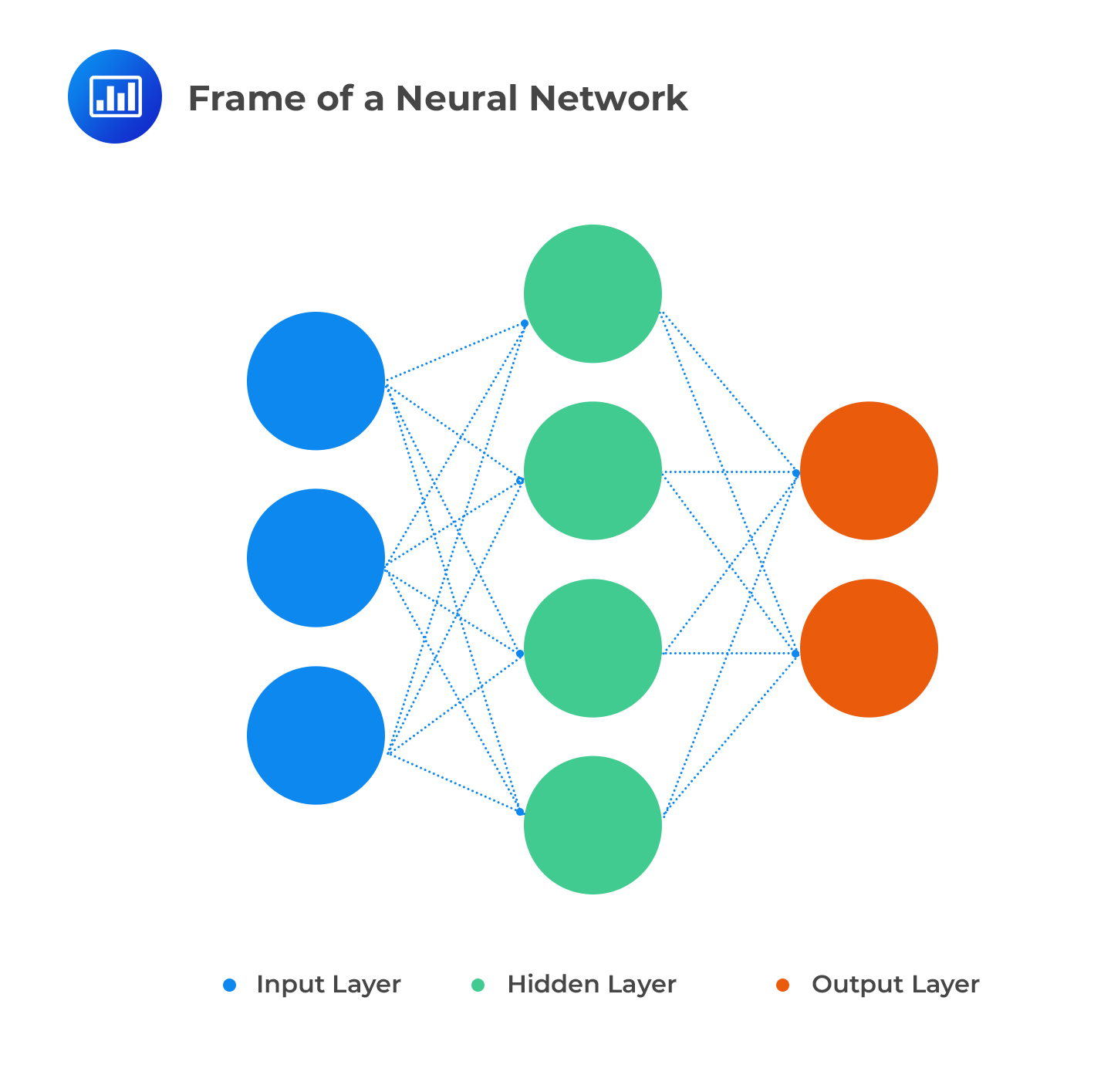
The basic structure of ANNs is made up of 3 layers:

• An input layer.
• One or more hidden layers.
• An output layer.

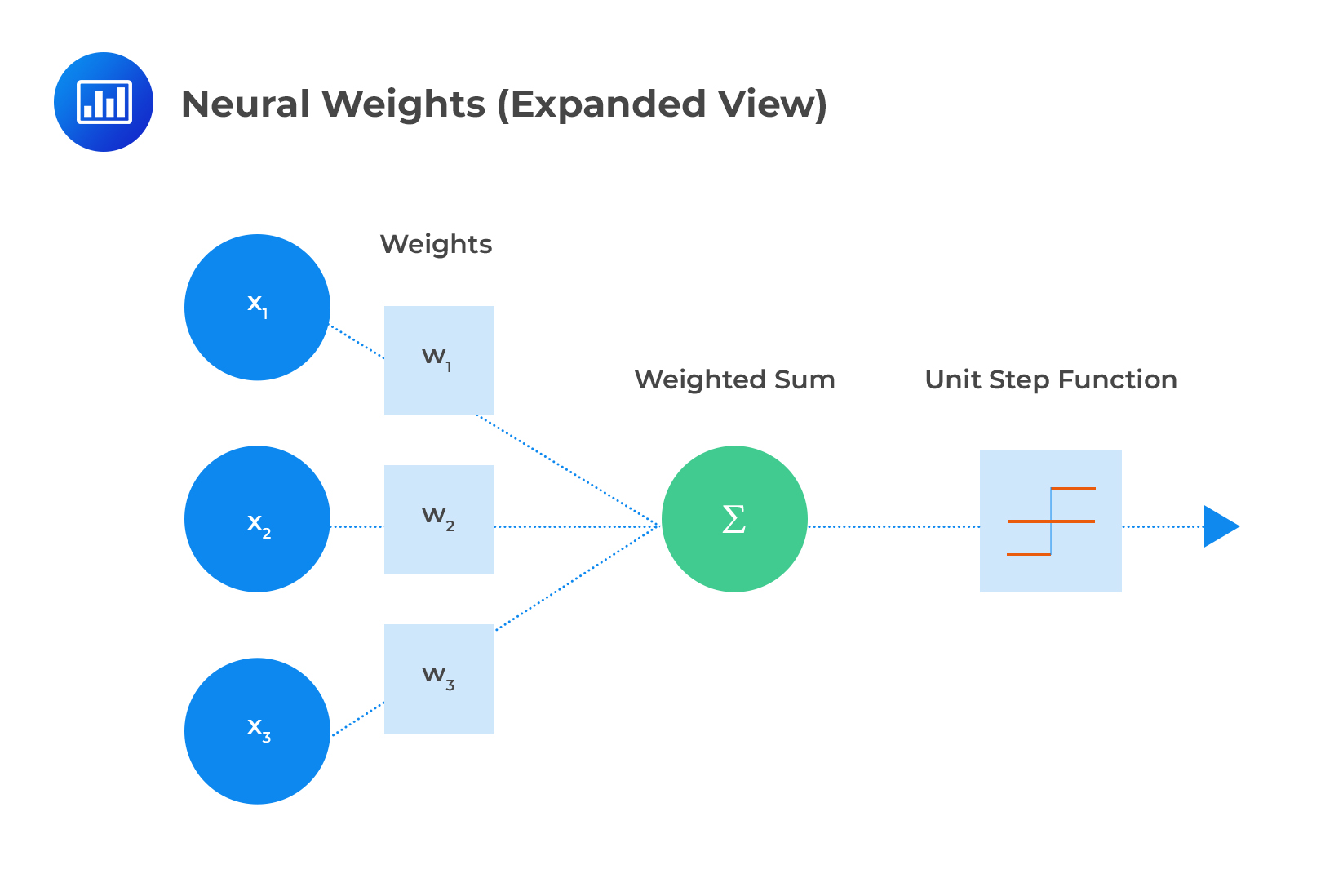
Each layer is made up of nodes. The input layer is designed to handle inputs, stimuli, and signals. The hidden layer is delegated to compute relationships and analyze data. The output later generates and delivers results to the user via a user interface. ANNs feature an intricate network where each node is connected with all the nodes in the next layer. Each connection has a particular weight to reflect the impact the preceding node has on the next node.

When all the node values from the input layer are multiplied by their weight and all this is summarized, we get some value for each green node in the hidden layer. Each node has an “activation function” (unit step function) that dictates whether it will be active and the amount of activity, based on the summarized value.

Neural networks are widely used in modern loan application software. Neural networks are used to underwrite a loan and decide whether to approve or reject the application. In fact, these application systems have been found to be more accurate compared to traditional methods in terms of assessing the failure (default) rate. To illustrate how this works, let’s look at some of the factors that can be used in such a loan application software.

Input factors: Age, marital status, gender, employment status, salary range, the total number of children, level of education, house ownership, number of cars owned, and region.

Target variable: Loan Approved (Yes or No).

Before the evaluation system can be used, the neural network must get trained by being fed with training input data. Once trained, the variable “Loan Approved” can be found using some test data not present in the training set (real-time data). This process is called supervised learning. In supervised learning, the original data used in the training process is a major determinant of model performance. The model must be refined to reduce misclassification errors that can result in inaccurate predictions. This is achieved by altering weights and connections at different nodes.

Neural networks have become popular in finance thanks to their ease of use and ability to generate a workable solution fairly quickly. They are used to predict bank fraud, bond ratings, the price of futures contracts, and much more.

Limits of ANN

1. Results are essentially developed in a “black box“. In other words, it is almost impossible to give a step-by-step explanation as to why and how a given result is obtained. All we can do is feed the network with data with well-distinguished profiles and expect some results.
2. They are also sensitive to input quality, so the data used to train the model must not be outlier data that significantly deviate from normal cases.
3. Neural networks work well with quantitative data but struggle to interpret qualitative data, especially when the variables are dichotomous and categorical.
4. There is no robust scientific way to determine if a neural network is optimally estimated. We can only rely on experience and scrutinize the assumptions adopted in the building process.
5. There’s a risk of over-fitting, where the network becomes too dependent on the training set such that it is incapable of producing reliable and satisfactory results when applied to other borrowers, sectors, geographical areas, or economic cycle stages. This problem is compounded by the fact that we do not have tests that can be performed to establish whether or not the solution is over-fitting. However, this problem can be mitigated by continuous re-launching of the training process and using new data.

The Role and Management of Qualitative Information in Assessing Probability of Default

Although most statistical models use quantitative data, assessment and prediction of the probability of default also require some qualitative data. These include:

• Sectors’ competitive forces characteristics.
• The firms’ competitive strengths and weaknesses.
• Management quality.
• Cohesion and stability of entrepreneurs and owners.
• Managerial reputation and succession plans in case of managerial/entrepreneurial resignation or turnaround.
• Growth and financing strategy.

These qualitative characteristics are especially useful when using judgment-based approaches to credit approval and can further be split into three classes:

1. Efficiency and effectiveness of internal processes (production, administration, marketing, marketing, and control).
2. Investment, technology, and innovation.
3. Human resource management, talent nurturing, and motivation.

Beyond the three main classes, some of the qualitative concepts that are widely assessed include:

• Product/service range.
• Main customers/Suppliers Group structure and the type and transparency of financial relationships between group members.
• Ongoing investments and their foreseeable financial results.
• Past use of extraordinary measures, such as government support.
• Technological innovation.
• Quality of financial reports.

Recommendations When Using Qualitative Data

Qualitative data can be intricate and complex and, therefore, an analyst should find ways to avoid complex calculations and information overlap. To achieve this:

• Only gather qualitative data that cannot be collected quantitatively. Growth and financial structure information, for instance, can be extracted from balance sheets.
• Use a simple yes/no binary system to indicate the presence or absence of an attribute.
• Binary indicators can be transformed into 0/1 ‘dummy variables’.
• Collect information in closed form, i.e., have a set of predefined answers.

Practice Question

Assume that Armenia Market has $230 million in assets and was issued a 10-year loan three years ago. The face value of the debt is $700 million. The expected return of the risky world is 11%,and the instantaneous assets value volatility is 18%. Compute the value of default probability following the Merton approach and applying the Black-Scholes-Merton formula.

A. 0.6028.

B. 0.1822.

C. 0.8311.

D. 0.2438.

The correct answer is C.

$$ PD=N\left( \frac { ln\left( F \right) -ln\left( { V }_{ A } \right) -\mu T+\frac { 1 }{ 2 } { \sigma }_{ A }^{ 2 }\times T }{ { \sigma }_{ A }\sqrt { T } } \right) $$

From the question, we have that:

\(F=$700,000,000\).

\({ V }_{ A }=$230,000,000\).

\(T=7\).

\({ \sigma }_{ A }=0.18\).

\(\mu =0.11\).

Therefore:

$$ \begin{align*}PD&=N\left( \frac { ln700,000,000-ln230,000,000-7\times 0.11+{ 1 }/{ 2 }\times { 0.18 }^{ 2 }\times 7 }{ 0.18\times \sqrt { 7 } } \right)\\ &\Rightarrow N(0.9583) = P(Z < 0.9583) = 0.8311 \end{align*}$$