Credit Risks and Credit Derivatives

After completing this reading, you should be able to:

• Use the Merton model to calculate the value of a firm’s debt and equity and the volatility of firm value.
• Explain the relationship between credit spreads, time to maturity, and interest rates and calculate credit spread.
• Explain the differences between valuing senior and subordinated debt using a contingent claim approach.
• Explain, from a contingent claim perspective, the impact of stochastic interest rates on the valuation of risky bonds, equity, and the risk of default.
• Compare and contrast different approaches to credit risk modeling, such as those related to the Merton model, CreditRisk+, CreditMetrics, and the KVM model.
• Assess the credit risks of derivatives.
• Describe a credit derivative, credit default swap, and total return swap.
• Explain how to account for credit risk exposure in valuing a swap.

Credit risk is the risk that is incurred when a creditor fails to make promised payments. The occurrence of a credit event has a negative effect on income and cash flows. One of the roles of a risk manager, therefore, is to assess the potential financial impact of a credit event and make a determination as to whether there’s need to hedge using derivatives or some other financial mechanism.

If a firm takes positions in derivatives, these instruments do have credit risk as well; they are not “safe havens” that have guaranteed cash flows. As such, it is important to consider the riskiness of the counterparty before taking a position in a derivative.

Derivative contracts whose payoffs depend on a specified credit event are called credit derivatives. For example, a credit derivative could promise to pay some amount in the event that JPMorgan Chase defaults, and nothing in case it doesn’t default.

Risk managers often use credit derivatives to hedge against credit risk.

In this chapter, we begin by looking at a common approach used to price debt claims based on the Black-Scholes option-pricing model that breaks down the determinants of such claims.

Using the Merton Model 

Calculating the Value of Equity

The Merton model is used to assess a company’s credit risk by modeling the company’s equity as a call option on its assets. It is built upon the Black-Scholes pricing model and seeks to establish a link between default and a firm’s capital structure.

In its simplest form, the Merton model makes a set of assumptions:

• The firm pays no dividends.
• There’s only one liability claim.
• Markets are perfect, meaning that there are no taxes, transaction costs, or any other cost in the process of taking up a contract.

These assumptions have certain implications. If the markets are perfect, for example, then the value of the firm equals the value of debt plus the value of equity.

In line with these assumptions, let’s assume that a firm has a single outstanding zero-coupon debt with a face value (principal amount) F, payable at time T. Now, there are two possible scenarios. First, the value of the firm at time T, \({\text{V}}_{\text{T}}\) could be large enough to pay the principal amount, in which case, shareholders have a claim over the balance, i.e., \({\text{V}}_{\text{T}}\)-F. Secondly, the value of the firm at time T could be insufficient such that the firm is unable to settle the principal amount, in which case, equity holders receive nothing.

Looking closely, the two possible scenarios and their payoffs pretty much resemble a call option, with the underlying instrument as firm value and the principal amount as the exercise price. The value of equity at time T can therefore be represented as:

$$ { \text{E} }_{ \text{T} }=\text{Max}\left( { \text{V} }_{ \text{T} }-\text{F},0 \right) $$

A simplified example will help further drive the concept home.

Example: Computing the Value of Equity

Assume that a firm has issued zero-coupon debt that requires it to pay $160m to debt holders at maturity. Further, assume that the firm has no other creditors. If the total value of the firm at maturity is $180m, what’s the firm’s value of equity? What is the value of equity given a firm value of $140m at maturity?

Solution

$$ { \text{E} }_{ \text{T} }=\text{Max}\left( { \text{V} }_{ \text{T} }-\text{F},0 \right) $$

In the first case,

$$ { \text{E} }_{ \text{T} }=\text{Max}\left( 180-160,0 \right) =20 $$

In the second case,

$$ { \text{E} }_{ \text{T} }=\text{Max}\left( 140-160,0 \right) =0 $$

The following figure illustrates the fact that the payoff for equity is equal to the payoff for a long call option.

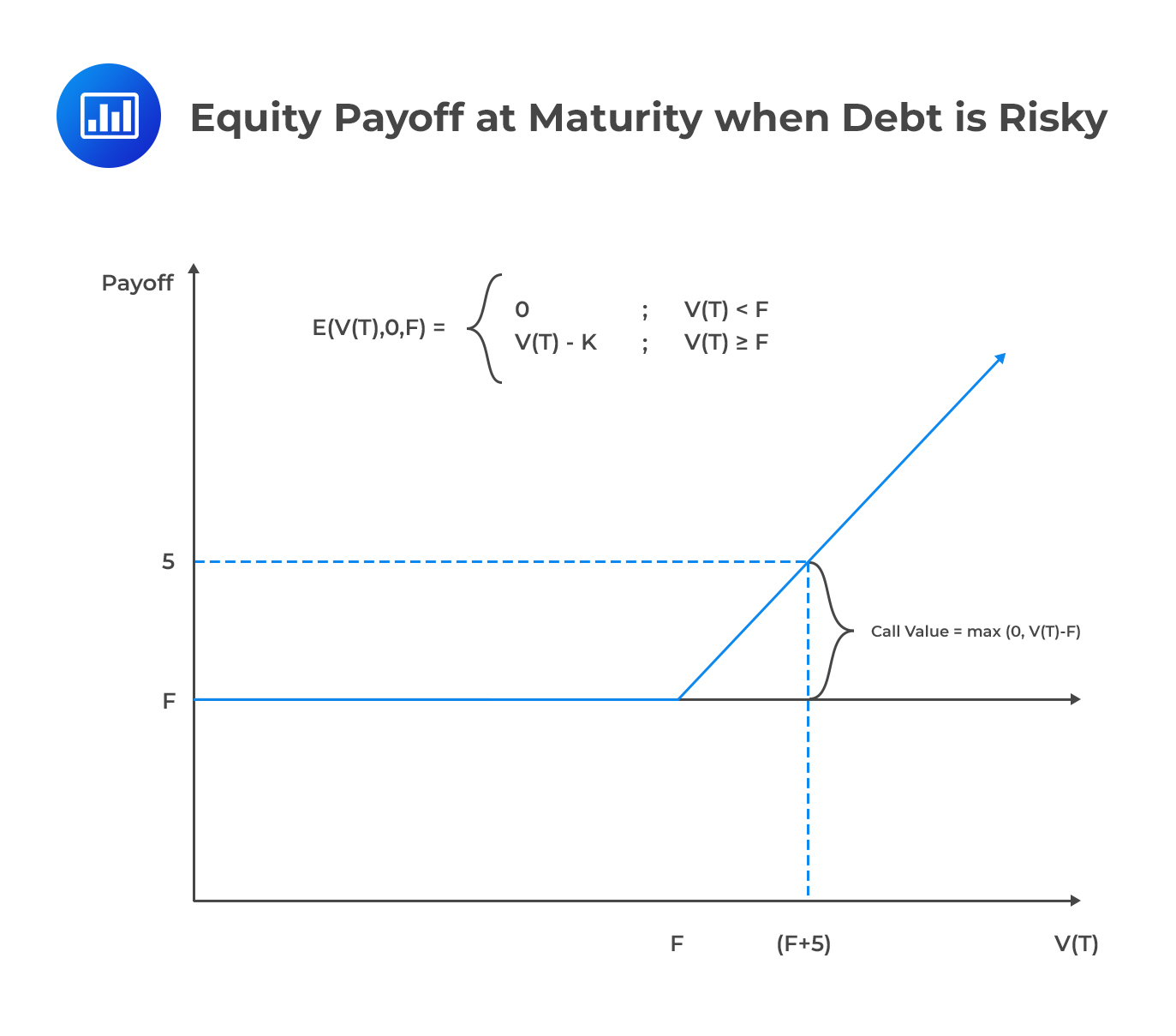Calculating the Value of Debt

How about the payoff for debt? If we assume that a debt is risk-free and payment of the principal amount F is guaranteed, the payoff would be F, regardless of firm value at maturity. In the presence of risk, however, the debt holder receives an amount lower than the anticipated payment if the firm value, \({\text{V}}_{\text{T}}\) is less than F. In other words, we are saying that if \({\text{V}}_{\text{T}} < \text F\) at maturity, then the amount received by the debt holder will be reduced by \(\text F-\text V_{\text T}\).

The payoff for debt is pretty much like that of a combination of a long position in a T-bill with a face value of F and a short position on the firm value with an exercise price of F. In other words, holders of risky debt effectively buy risk-free debt and write a put option on the value of the firm with an exercise price equal to the face value of the debt. We can therefore represent the value of debt, \({\text{D}}_{\text{T}}\), as follows:

$$ { \text{D} }_{ \text{T} }=\text{F}-\text{max}\left( \text{F}-\text{V}_{ \text{T} },0 \right) $$

Example: Computing the Value of Debt

Assume that a firm has issued zero-coupon debt that requires it to pay $160 million to debt holders at maturity. In addition, assume that the firm has no other creditors. If the total value of the firm at maturity is $180m, what’s the firm’s value of debt? What is the value of debt given a firm value of $140m at maturity?

Solution

$$ { \text{D} }_{ \text{T} }=\text{F}-\text{max}\left( \text{F}-\text{V}_{ \text{T} },0 \right) $$

In the first case,

$$ { \text{D} }_{ \text{T} }=160-\text{max}\left( 160-180,0 \right) =160 $$

In the second case,

$$ { \text{D} }_{ \text{T} }=160-\text{max}\left( 160-140,0 \right) =140 $$

Note: It would also be correct to look at the payoff for debt as the value of a firm minus the payoff of a call option with exercise price equal to the principal amount of the debt.

To price the equity and the debt using the Black-Scholes formula for the pricing of a European call, we need to make additional assumptions:

• Firm value is characterized by a lognormal distribution with constant volatility, \(\sigma\).
• The interest rate, r, is constant.
• Trading is continuous.

Merton’s Formula for the Value of Equity

Using E(V, F, T, t) to represent the value of equity,

$$ \text{E}\left(\text {V,F,T,t}\right) =\text{V}\times \text{N}\left( \text{d} \right) -{ \text{Fe} }^{ { -\text{r} }^{ \left( \text{T-t} \right) } }\times \text{N}\left( \text{d}-\sigma \sqrt { \text{T-t} } \right) $$

Where:

$$ \text{d}=\cfrac { \text{ln}\left( \cfrac { \text{V} }{ { { \text{Fe} } }^{ { -{ \text{r} } }^{ \left( { \text{T-t} } \right) } } } \right) }{ \sigma \sqrt { \text{T-t} } } +\cfrac { 1 }{ 2 } \sigma \sqrt { \text{T-t} } $$

V = Value of the firm.

F = Face value of the firm’s zero-coupon debt maturing at T (only liability).

\(\sigma\) = Volatility of the value of the firm.

r = Annual interest rate.

N = Cumulative normal distribution.

Example: Computing the Value of Equity

A firm has a current value of $100 million. Its only outstanding debt is a 3-year zero-coupon bond with a face value of $80 million. Compute the value of the firm’s equity at time=t given the following information:

• Annual interest rate = 5%.
• Volatility of the firm = 10%.

$$ \begin{align*} \text{E}\left(\text {V,F,T,t}\right) & =\text{V}\times \text{N}\left( \text{d} \right) -{ \text{Fe} }^{ { -\text{r} }^{ \left( \text{T-t} \right) } }\times \text{N}\left( \text{d}-\sigma \sqrt { \text{T-t} } \right) \\ & =100\times \text{N}\left( \text{d} \right) -80{ \text{e} }^{ -0.05\times 3 }\times \text{N}\left( \text{d}-0.1\sqrt { 3 } \right) \\ \text{d} & =\cfrac { \text{ln}\left( \cfrac { \text{V} }{ { { \text{Fe} } }^{ { -{ \text{r} } }^{ \left( { \text{T-t} } \right) } } } \right) }{ \sigma \sqrt { \text{T-t} } } +\cfrac { 1 }{ 2 } \sigma \sqrt { \text{T-t} } \\ & =\cfrac { \text{ln}\left( \cfrac { 100 }{ 80{ { \text{e} } }^{ -0.05\times 3 } } \right) }{ 0.1\sqrt { 3 } } +\cfrac { 1 }{ 2 } 0.1\sqrt { 3 } =2.15435+0.086603=2.2410 \\ \text{E}\left(\text {V,F,T,t}\right) & = 100\times \text{N}\left(2.2410 \right)-68.85664 \times \text{N} \left(2.0678 \right) \end{align*} $$

From probability tables, \(\text{N}(2.241) = 0.9875 \text{ and } \text{N}(2.0678) = 0.9807\)

$$ \text{E}(\text{V,F,T,t})=98.75-67.52767=31.2223 $$

The value of equity is $31.2223 million

Note: The formula can also be computed as follows:

$$ { \text{E} }\left( { \text{V,F,T,t} } \right) =\text{V}\times \text{N}\left( { \text{d} }_{ 1 } \right) -{ { \text{Fe} } }^{ { -{ \text{r} } }^{ \left( { \text{T-t} } \right) } }\text{N}\left( { \text{d} }_{ 2 } \right) $$

Where:

$$ \begin{align*} { \text{d} }_{ 1 } & =\cfrac { \text{ln}\cfrac { \text{V} }{ \text{F} } +\left( \text{r}+\cfrac { { \sigma }^{ 2 } }{ 2 } \right) \left( \text{T-t} \right) }{ \sigma \sqrt { \text{T-t} } } \\ { \text{d} }_{ 2 } & ={ \text{d} }_{ 1 }-\sigma \sqrt { \text{T-t} } \end{align*} $$

and everything else defined as before.

Merton’s Formula for the Value of Debt

There are two ways to compute the value of debt. First, we can use the fact that the payoff of risky debt equals the payoff of risk-free debt less the payoff of a put option on the firm with the face value of the debt as the exercise price. Using D(V,F,T,t) to represent the value of debt and p(V,F,T,t) to represent the price of the put option at time t,

$$ { \text{D} }\left( { \text{V,F,T,t} } \right) =\text{P}\left( \text{T} \right) \text{F}-{ \text{p} }\left( { \text{V,F,T,t} } \right) $$

Where \(\text{P}\left(\text{T}\right)\) is the price of a discount bond that matures at T.

Example: Computing the Value of Debt

A firm has a current value of $100 million. Its only outstanding debt is a 3-year zero-coupon bond with a face value of $80 million. Compute the value of the firm’s debt at t as a portfolio of risk-free debt and a short position in a put-on firm value with an exercise price of the face value of debt. You have been given the following information:

• Annual interest rate = 5%.
• Volatility of the firm = 10%.

Solution

We have already established the value of equity as $31.2223 million.

$$ \begin{align*} { \text{D} }\left( { \text{V,F,T,t} } \right) & = { \text{Fe} }^{ { -\text{r} }^{ \left( \text{T-t} \right) } } -{ \text{p} }\left( { \text{V,F,T,t} } \right) \\ & = 80{ \text{e} }^{ -0.05\times 3 }-{ \text{p} }\left( { \text{V,F,T,t} } \right) \\ & = 80 \times 0.8607-{ \text{p} }\left( { \text{V,F,T,t} } \right) \\ & =68.86-{ \text{p} }\left( { \text{V,F,T,t} } \right) \end{align*} $$

Using put call parity, we can determine the value of the put:

$$ \begin{align*} { \text{p} }\left( { \text{V,F,T,t} } \right) & = {\text{c}}_{\text{t}} + { \text{Fe} }^{ { -\text{r} }^{ \left( \text{T-t} \right) } } -V \\ & = 31.2223+80{ \text{e} }^{ -0.05\times 3 }-100 \\ & = 0.078938 \\ { \text{D} }\left( { \text{V,F,T,t} } \right) & = 68.86-0.078938=$68.78 \\ \end{align*} $$ 

The second method that can be used to determine the value of debt is by simply subtracting the value of equity from the value of the firm. In the example above, the value of the firm is $100m, while the value of equity is $31.2223m. The difference gives us the value of debt ($68.78m).

For a given value of the firm, the value of the debt is a decreasing function of the value of equity, which is the value of a call option on the value of the firm. Holding everything else equal, therefore, the table below summarizes how the value of debt and the value of equity are affected by various inputs under the Merton model:

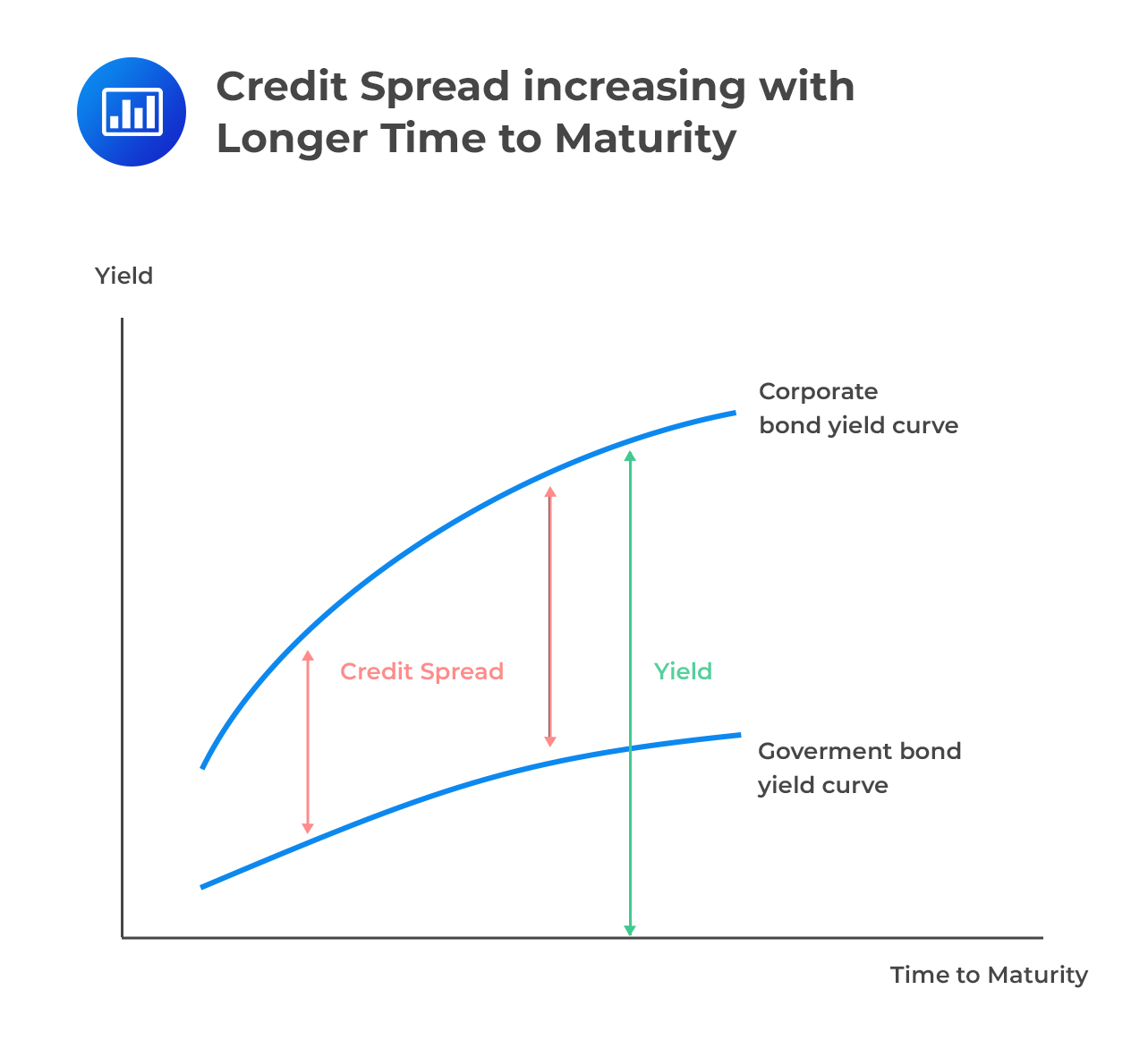
Relationship among Credit Spreads, Time to Maturity, and Interest Rates

Credit spread is the difference between the yield on risky debt and the yield on risk-free debt. For example, assume that an A-rated corporate bond with an A rating has a yield of 10% while a U.S. T-bond of the same maturity has a yield of 8%. In this case, the credit spread for A-rated debt of 2% (= 8% – 10%). Generally, investors require a higher yield as a precondition for taking a higher risk.

By analyzing credit spreads across rating classes, we can establish how the yield of risky debt compares to that of risk-free debt.

Credit spread can be calculated using the following formula:

$$ \text{Credit Spread}=-\left( \cfrac { 1 }{ \text{T-t} } \right) \text{ln}\left( \cfrac { \text{D} }{ \text{F} } \right) -\text{r} $$

Where:

\(\left({\text{T-t} } \right)\) = time remaining to maturity.

D = Current value of debt.

F = Face value of debt.

R = Risk-free rate of interest.

Example: Computing the Credit Spread

A firm has a zero-coupon bond maturing in 5 years. Assume that the face value of this debt is $100 million, with a current value of $88 million. Compute the credit spread, assuming a risk-free rate of 1.5%.

$$ \begin{align*} \text{Credit Spread} & =-\left( \cfrac { 1 }{ \text{T-t} } \right) \text{ln}\left( \cfrac { \text{D} }{ \text{F} } \right) -\text{r} \\ & = -\left( \cfrac { 1 }{ 5 } \right) \times \text{ln} \left( \cfrac { 88 }{ 100 } \right) -0.05=0.01057=1.057\% \end{align*} $$

As the time to maturity increases, credit spreads for both high-rated and low-rated bonds tend to increase. That happens because as time increases, so does a range of risks and other intervening events that increase the probability of receiving an amount less than par.

In addition, the expected value of a firm at maturity increases as the risk-free rate increases and, therefore, the risk of default decreases. Credit spreads tend to narrow as the risk of default decreases.

Determining Firm Value and Volatility

In situations where all the debts outstanding are traded, determining the value of debt would be a straightforward process. We would only need to compute the value of a put option on the firm with the appropriate strike price. In reality, however, firms often have a mix of traded and non-traded claims, and that means it is not possible to trade a portfolio of securities that represent a claim on the firm as a whole. This creates two problems: (I) it is impossible to value a firm directly, and (II) it is impossible to come up with a hedge against a claim whose value depends on the value of the firm.

Fortunately, the Merton model can help us get around these deficiencies. To do this, however, we have to assume that small changes in the return on equity are perfectly correlated with the value of a firm; that any change in the return on equity is proportional to the change in the value of the firm.

The value of a firm is equivalent to a call option on the firm and a risk-free asset. It follows that a small change in the value of the firm changes the value of equity by delta, Δ, times the change in firm value. If you recall, delta is the change in the price of the option based on a $1 change in the value of the underlying asset – in the context of stocks. The interpretation here is no different. The Merton model delta is equal to \(\text{N}\left( \text{d} \right)\).

$$ \Delta =\cfrac { \text{change in value of call option} }{ \text{change in value of underlying asset} } =\text{N}\left( \text{d} \right) $$

So, we can calculate a firm’s value provided we have the parameters to determine the value of equity as a call option and the value of risk-free debt.

The Merton model delta increases as the call option gets more in the money as the value of a firm increases. However, the change in the value of equity is not constant; it decreases as firm value increases. This phenomenon is sometimes known as volatility smirk. It violates one of the assumptions under the Black-Scholes-Merton model – that volatility of the underlying is constant.

Provided we know the value of equity and the value of an option on firm equity, it is possible to use an iterative process to determine firm value as well as firm volatility.

Differences between Valuing Senior and Subordinated Debt Using a Contingent Claim Approach

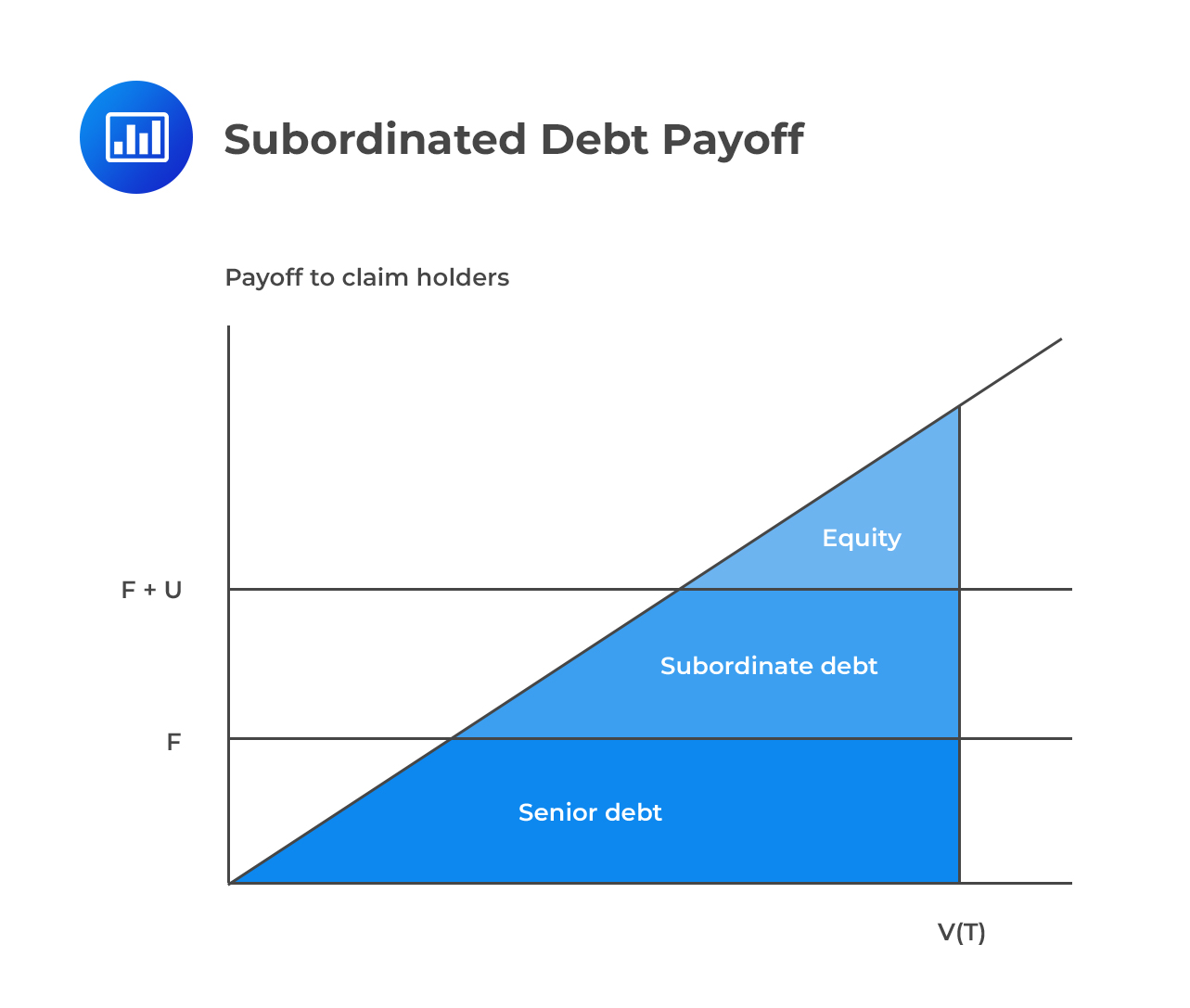
Subordinated debt is a debt that ranks after other (senior) debts if a firm falls into liquidation or bankruptcy. In other words, subordinated debt holders will only get paid after all obligations to senior debt holders have been paid. Subordinated debt is, therefore, considered riskier than senior debt and is more like an equity claim than a debt claim. It follows that an increase in firm volatility makes it more likely that subordinated debt will be paid off and therefore increases the value of subordinated debt. When firm volatility increases, senior debt always falls in value.

To understand the determinants of the value of subordinated debt, let’s consider a firm that’s financed as follows:

• One issue of senior debt, denoted D, with face value F.
• One issue of subordinated debt, denoted SD, with face value U.
• Equity, S.

In these circumstances, equity is considered an option on the value of a firm with exercise price U + F because shareholders receive nothing unless the value of the firm exceeds U + F.

The value of the firm is:

$$ { \text{V} }= { \text{D} }\left( { \text{V,F,T} } \right) +{\text{SD} }\left( { \text{V,U,T,t} } \right) +\text{S}\left( { \text{V,U+F,T,t}} \right) $$

The value of equity is given by call option pricing formula:

$$ \text{S}\left( { \text{V,U+F,T,t}} \right) =\text{c}\left( { \text{V,U+F,T,t}} \right) $$

Collectively, shareholders and subordinated debt holders receive the excess of firm value over the face value of the senior debt, F, if that excess is positive. Therefore, they have a call option on V with strike price equal to F. This implies that the value of the senior debt is the value of the firm V minus the value of the option held by equity and subordinated debt holders:

$$ \text{D}\left( { \text{V,F,T,t}} \right) = \text{V} -\text{c}\left( { \text{V,F,T,t}} \right) $$

With the values of equity and debt already determined, the value of subordinated debt can be obtained by subtracting the value of the equity and that of the senior debt from the value of the firm.

$$ \begin{align*} { \text{SD} }\left( { \text{V,U,T,t }} \right) & =\text{V}-\text{c}\left( { \text{V,F+U,T,t}} \right) -\left[ \text{V}-\text{c}\left( { \text{V,F,T,t}} \right) \right] \\ & =\text{c}\left( { \text{V,F,T,t}} \right) – \text{c} \left[{ \text{V,F+U,T,t}} \right] \end{align*} $$

Note that the second formula gives yet another route to the value of subordinated debt: a long position in a call option on a firm with strike price equal to the face value of senior debt, F, and a short position on a call option on the firm with a strike price equal to the total principal due on total debt, U + F.

Example: Computing the Value of Subordinated Debt

A firm valued at $140 million has subordinated debt with a face value of $60 million, and senior debt with a face value of $100 million, both maturing in 5 years. The interest rate is 10 percent, and the volatility is 20 percent. Determine the value of subordinated debt.

Solution

We can summarize the information as follows:

$$ \textbf{Summary of Data} $$

$$ \begin{array}{c|c} \text{V} & {$140 \text m} \\ \hline \text{F} & {$100 \text m} \\ \hline \text{U} & {$60 \text m} \\ \hline \text{T} & {5 \text{ years}} \\ \hline {\sigma} & {20\%} \\ \end{array} $$

If we ignore subordinated debt, the call option is worth $79.73 million. This is the value of equity. Therefore, the value of senior debt is $60.27 million (= 140M – 79.73M).

$$ \textbf{Option with strike at F} $$

$$ \begin{array}{c|c} \textbf{Face value of debt} & $\textbf{100 m} \\ \hline {{ \text d }_{ 1 }} & {1.865} \\ \hline {\text{Nd }_{ 1 }} & {0.9689} \\ \hline {{ \text d }_{ 2 }} & {1.418} \\ \hline {\text{Nd }_{ 2 }} & {0.9218} \\ \hline {\text c\left( \text{V,F,T,t} \right)} & {79.73} \\ \end{array} $$

Without ignoring subordinated debt, the call option is worth $48.2 million. This is the actual value of equity. Therefore, the value of subordinated debt is $31.53 million (= 79.73M – 48.2M).

$$ \textbf{Option with strike at F+U} $$

$$ \begin{array}{c|c} \textbf{Face value of debt} & {$160 \text m} \\ \hline {{ \text d}_{ 1 }} & {1.395} \\ \hline {\text{Nd}_{ 1 }} & {0.9185} \\ \hline {{\text d}_{ 2 }} & {0.948} \\ \hline {\text{Nd}_{ 2 }} & {0.8283} \\ \hline {\text c \left( \text{V,F+U,T,t} \right)} & {48.20} \\ \hline {\text c\left(\text{V,F,T,t} \right)}-{\text c\left( \text{V,F+U,T,t} \right)} & {31.53} \\ \end{array} $$

As we have seen in the example above, the value of subordinated debt corresponds to two options: a long position in a call option that increases in value with volatility and a short position in a call option that becomes costlier as volatility increases. This scenario leads to ambiguous comparative statics for the value of subordinated debt.

If the value of the firm is low, there’s a good chance that subordinated debt will not pay off. In these circumstances, the short position in the call option is economically important. As a result, subordinated debt is almost similar to equity, and its value is an increasing function of the volatility of the firm.

If the value of a firm is high, there’s a high chance that subordinated debt will pay off. In these circumstances, subordinated debt is almost similar to senior debt, and inherits the characteristics of senior debt. i.e, its value is a decreasing function of volatility. The following figure summarizes how various capital components are impacted by inputs of the Merton model.

The Impact of Stochastic Interest Rates on the Valuation of Risky Bonds

Before making a decision on whether or not to hedge a debt position, it is important to take the interaction between interest rate changes and firm value changes. The big question is, why?

As you will recall, one of the assumptions we have worked with under the Merton model is that interest rates are constant. In reality, however, interest rates are stochastic; they keep on changing. Stochastic interest rates affect the value of debt in two ways:

• An increase in interest rates decreases the value of debt by decreasing the present value of the anticipated coupon payments.
• An increase in interest rates has the potential to affect firm value. Studies have shown that when interest rates rise, stock prices fall, i.e., there’s a negative correlation between interest rates and stock prices.

One of the models that allow for stochastic interest rates is the Vasicek model. The model actually allows interest rate to revert to a long-run mean. Under the model, the change in interest rates at time t is given by:

$$ { \Delta }\text{r}_{ \text{t} }=\lambda \left( \text{k-r}_{ \text{t}} \right) \Delta \text{t}+{ \sigma }_{\text{r}}{ \varepsilon }_{\text{t} } $$

Where:

\(\text{r}_{ \text{t} }\) is the current interest rate.

\({ \varepsilon }_{\text{t} }\) is a random shock.

K = Speed at which the interest rates reverts to the long-run value θ.

\({ \sigma }_{\text{r}}\) = Interest rate volatility.

Shimko, Tejima, and Van Deventer (1993) provide us with a variant of the Merton model that recognizes the correlation between firm value and interest rate changes. According to their model the value of risky debt is given by the following:

$$ \begin{align*} \text{D}\left( { \text{V,r,F,t,T} } \right) & =\text{V}-\text{VN}\left( { \text{h} }_{ 1 } \right) +\text{F}{ \text{P} }_{ \text{t} }\left( \text{T} \right) \text{N}\left( { \text{h} }_{ 2 } \right) \\ \sigma \left( \text{s} \right) & =-\cfrac { 1-{ \text{e} }^{ -\text{ks} } }{ \text{k} } { \delta }_{ \text{r} }\\ { \text{V} }^{ 2 }\left( \text{s} \right) & ={ \delta }^{ 2 }+{ \sigma \left( \text{s} \right) }^{ 2 }-2\rho \delta \sigma \left(\text{s} \right) \end{align*} $$

$$ \begin{align*} \text{Q} & =\left(\text{T-t} \right) { \left( { \sigma }^{ 2 }+\cfrac { { \sigma }_{ \text{r} }^{ 2 } }{ {\text{k} }^{ 2 } } +\cfrac { { 2\rho \sigma \sigma }_{ \text{r} } }{ \text{k} } \right) }+\left( { { \text{e} } }^{ { -\text{k} }^{ \left( { \text{T-t} } \right) } }-1 \right) \left( \cfrac { { 2\sigma }_{ \text{r} }^{ 2 } }{ { \text{k} }^{ 3 } } +\cfrac { { 2\rho \sigma \sigma }_{ \text{r} } }{ \text{k} } \right) -\cfrac { { \sigma }_{ \text{r} }^{ 2 } }{ { 2\text{k} }^{ 3 } } \left( { { \text{e} } }^{ { -\text{k} }^{ \left( {\text{T-t} } \right) } }-1 \right) \\ {\text{h} }_{ 1 } & =\cfrac { \text{ln}\left( \cfrac { \text{v} }{ { \text{p} }_{ \text{t} }\left( \text{T} \right) \text{F} } \right) +0.5\text{Q} }{ \sqrt { \text{Q} } } \\ { \text{h} }_{ 2 } & ={ \text{h} }_{ 1 }-\sqrt { \text{Q} } \\ \end{align*} $$

Critique of the Merton Model

In practice, firms have complex capital structures usually consisting of a variety of debt instruments with different maturities and different coupon rates. For this reason, applying the Merton model is difficult. Remember that the Merton model assumes that there’s only one noncallable zero-coupon bond, default can occur only at maturity, and if there’s subordinated debt, there’s strict absolute seniority of claims. The Merton model is often seen as underestimating the actual corporate spreads.

In addition, one of the inherent assumptions under the Merton model is that there’s zero chance of a jump in the value of a firm. In reality, most of the default events witnessed catch us by surprise, and the inability to have jumps in the firm value in the Merton model implies defaults are too predictable. That’s hardly true.

Jones, Mason, and Rosenfield (1984) assert that the Merton model is outsmarted and outperformed by a naïve model in predicting default risk with respect to investment-grade bonds. However, the Merton model outperforms the naïve model for non-investment grade bonds.

These challenges have driven analysts and scholars to come up with alternative models, such as the KMV model, that can be able to predict default with much more accuracy.

Probability of Default and Loss Given Default under the Merton Model

To determine the value of debt in practice, we would need to have both the probability of default and the recovery rate. However, these two can only be estimated when the debt instruments are publicly traded because the current price can easily be observed. In the absence of credible trading data, therefore, the estimation of the PD and LGD is quite challenging.

To estimate the probability of default and the LGD, the Merton model makes two crucial assumptions:

1. Firm value is lognormally distributed with a constant volatility.
2. The firm has only one liability – the zero-coupon debt issue.

$$ \text {probability of default}=\text{N}\left( \cfrac { \text{ln}\left( \text{F} \right) -\text{ln}\left( \text{V} \right) -\mu (\text{T-t})+0.5{ \sigma }^{ 2 }(\text{T-t}) }{ \sigma \sqrt { \text{T-t} } } \right) \\ $$

Where:

\(\mu\) is the expected return on the value of the firm.

N is the cumulative normal distribution.

F is the face value of debt.

V is the value of the firm.

T is the maturity date.

\(\sigma\) is the volatility of firm value.

The LGD is given by:

$$ \text{LGD}=\text F\times \text{PD}-{\text {Ve} }^{ \mu \left( T-t \right) }\times \text{N}\left( \cfrac { \text{ln}\left( \text{F} \right) -\text{ln}\left( \text{V} \right) -\mu (\text{T-t})-0.5{ \sigma }^{ 2 }(\text{T-t}) }{ \sigma \sqrt { \text{T-t} } } \right) $$

Example: Computing the Probability of Default and the Loss Given Default

A firm has a current value of $100 million. Its only outstanding debt is a 3-year zero-coupon bond with a face value of $80 million. Compute (I) the probability that the firm will default on its debt, and (II) the expected LGD.

• Current interest rate = 5%.
• Expected return on firm assets = 20%.
• Volatility of the firm = 30%.

Solution

$$ \begin{align*} \text {probability of default} & =\text{N}\left( \cfrac { \text{ln}\left( \text{F} \right) -\text{ln}\left( \text{V} \right) -\mu (\text{T-t})+0.5{ \sigma }^{ 2 }(\text{T-t}) }{ \sigma \sqrt { \text{T-t} } } \right) \\ & =\text{N}\left( \cfrac { \text{ln}\left( 80 \right) -\text{ln}\left( 100 \right) -0.2(3)+0.5\left( { 0.3 }^{ 2 } \right) (3) }{ 0.3\sqrt { 3 } } \right) \\ & =\text{N}\left( -1.3243 \right) =1-\text{N}\left( 1.3243 \right) =1-0.9073=0.0927=9.27\% \end{align*} $$

$$ \begin{align*} \text{LGD} & =\text F\times \text{PD}-{ \text{Ve} }^{ \mu \left( \text T-\text t \right) }\times \text{N}\left( \cfrac { \text{ln}\left( \text{F} \right) -\text{ln}\left( \text{V} \right) -\mu (\text{T-t})-0.5{ \sigma }^{ 2 }(\text{T-t}) }{ \sigma \sqrt { \text{T-t} } } \right) \\ & =80\left( 0.0927 \right) -{ 100\text{e} }^{ 0.2\times 3 }\times \text{N}\left( \cfrac { { \text{ln} }\left( { 80 } \right) -{ \text{ln} }\left( { 100 } \right) -0.2({ 3 })-0.5\left( { 0.3 }^{ 2 } \right) (3) }{ 0.3\sqrt { { 3 } } } \right) \\ & =7.416-182.2119\times \text{N}\left( -1.8439 \right) \\ & =7.416-182.2119\times \left( 1-0.9673 \right) \\ & =7.416-182.2119\times 0.0327\\ & =$1.4577 \text m \end{align*} $$

Credit Risk Portfolio Models

Credit risk models have been developed to get around some of the weaknesses of the Merton model. If you recall, the Merton model assumes that there’s only one debt instrument, but that’s hardly true in practice. The model is not suitable for measuring the risk of a portfolio of debt claims.

The measurement of the credit risk of a portfolio of debt claims is markedly different from the measurement of the risk of other assets, e.g., equities. But why is this the case?

• Most debt securities are illiquid and, therefore, there’s no way to observe prices at a high frequency. That means analysts cannot rely on historical data of individual credit instruments to measure risk.
• The distribution of bond returns is not normal since the debtholder’s cash inflows are limited to the face amount plus coupons.
• Debt is issued by creditors who have not floated equity.
• Debt is not marked to market in contrast to traded securities. Without marking to market, a loss is only recognized if a default occurs.

The models that have been developed as alternatives to the Merton model take different approaches to tackle the above difficulties. We look at the most popular ones below.

CreditRisk+

The CreditRisk+ model measures the credit risk of a portfolio using a set of common risk factors for each obligor. Each obligor shows unique sensitivity to each of the common risk factors. It is imperative to note that the model allows for only two outcomes for a loss of a fixed size: default or no default. The probability of default for each obligor is a function of:

• The obligor’s credit rating.
• The realization of K risk factors.
• The sensitivity of the obligor to risk factors.

Conditional on the risk factors, the model assumes that defaults are uncorrelated across obligors.

Conditional probability of default for an obligor is the probability of default given the realizations of the risk factors. Unconditional probability of default, on the other hand, is the one obtained when the realizations of the risk factors are unknown.

The common risk factors used in the model can only take positive values and are scaled to have a mean of 1. In addition, the distribution of the risk factors is assumed to be known.

CreditMetrics^TM

The CreditMetrics^TM model is useful when the goal is to assess portfolio risk due to changes in debt value resulting from changes in obligor credit quality. The model recognizes changes in value caused not just by possible default events, but also by upgrades and downgrades in credit quality.

Under CreditMetrics, the distribution of the value of the debt claims must be established. To achieve that, the value of the bond for each rating class in a year is computed and the probability that the bond will end up in each one of those rating classes is assigned. This leads to a VaR measure for the portfolio. These probabilities are based on observed historical data.

The model makes 3 key assumptions:

• Firms within the same rating class have the same default rate and the same transition probabilities.
• The actual default rates are set equal to the historical default rate (migration frequencies).
• Default is defined in a statistical sense (non-firm specific) without explicit reference to the event which leads to default.

When using the CreditMerics approach to compute the VaR of a portfolio, the main challenge lies in the computation of the joint distribution of the migrations of the bonds in the portfolio. One solution to this problem involves using historical estimates for the joint probabilities of bond migrations. Looking at historical data, for example, we could figure out the frequency with which BBB bonds and B bonds, respectively, move to a BB rating and a CCC rating.

The KMV Model

The KMV model makes direct use of the Merton model in the computation of the probability of default, PD. It derives PD using the “expected default frequency” for each obligor. Unlike the Merton model, however, the KMV model assumes a more complicated capital structure that includes equity, short-term debt, long-term debt, and convertible debt.

Perhaps, the biggest advantage that comes with the use of the KMV model is the fact that it uses current equity values. As such, the impact of a current event does have an effect on the probability of default. In practice, rating migrations occur with a considerable lag; they are reactive. The use of current values implies that the PD changes continuously. This is in direct contrast with the CreditMetrics model where firm value can change without any impact on the probability of default.

Credit Derivatives

Credit derivatives are financial instruments that transfer credit risk of an underlying portfolio of securities from one party to another party without transferring the underlying portfolio. They are usually privately held, negotiable contracts between two parties. A credit derivative allows a creditor to transfer the risk of the debtor’s default to a third party.

Credit derivatives are over-the-counter instruments. This means that they are non-standardized and their trading is not bound by the Securities and Exchange Commission regulations.

The main types of credit derivatives include:

• Credit default swaps.
• Collateralized debt obligations.
• Collateralized loan obligations.
• Total return swaps.
• Credit spread swap options.

For most credit derivatives, the payoff depends on the occurrence of a credit event for a reference entity. A credit event can be:

• Failure to make a required payment.
• A restructuring that makes any creditor of the entity worse off.
• Invocation of the cross-default clause.
• Bankruptcy.

Credit Default Swaps (CDS)

In a CDS, one party makes payments to the other and receives, in return, the promise of compensation if a third party defaults.

Example: Credit Default Swap

Assume that Bank A buys a bond issued by ABC Company. In order to hedge the default of ABC Company, Bank A could buy a credit default swap (CDS) from insurance company X. The bank keeps making fixed periodic payments (premiums) to the insurance company, in exchange for the default protection.

Debt securities often have lengthy terms to maturity, sometimes as long as 30 years. It is very difficult for a creditor to come up with reliable credit risk estimates over such a long investment period. For this reason, credit default swaps have over the years become a popular risk management tool. As of June 2018, for example, a report by the office of the U.S. Comptroller of the Currency placed the size of the entire credit derivatives market at $4.2 trillion, of which credit default swaps accounted for $3.68 trillion (approx. 88%).

Like other derivatives, the payoff of a CDS is contingent upon the performance of an underlying instrument. The most common underlying instruments include corporate bonds, emerging market bonds, municipal bonds, and mortgage-backed securities.

The value of a CDS rises and falls as opinions change about the likelihood of default. In fact, an actual event of default might never occur. A default event can be difficult to define when dealing with CDSs. Although bankruptcy is widely seen as the “de facto” default, there are companies that declare bankruptcy and yet proceed to pay all of their debts. Furthermore, events that fall short of default can also cause damage to a creditor. These events include late payments or payments made in a form different from what was promised. Trying to determine the exact extent of damage to a creditor when some of these events happen can be difficult. CDSs are designed to protect creditors against such credit events.

Total Return Swaps

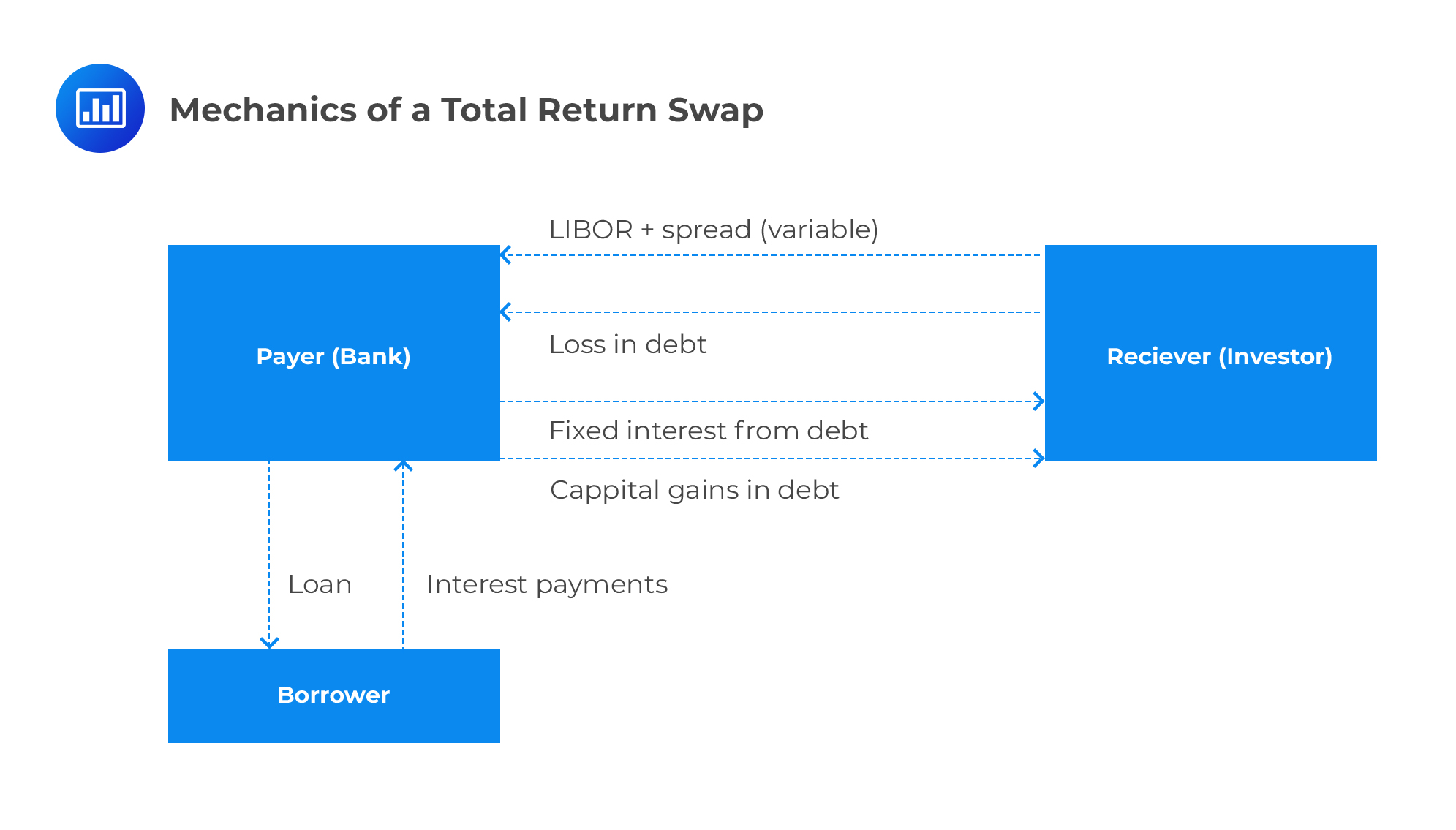
A total return swap is a credit derivative that enables two parties to exchange both the credit and market risks. In a total return swap, one party, the payer, is able to confidentially remove all the economic exposure of the asset without having to sell it. The receiver of a total return swap, on the other hand, is able to access the economic exposure of the asset without having to buy it.

For example, consider a bank that has significant (but risky) assets in the form of loans in its books. Such a bank may want to reduce its economic exposure with respect to some of its loans while still retaining a direct relationship with its customer base. The bank can enter into a total return swap with a counterparty that desires to gain economic exposure to the loan market. What happens is that the bank (payer) pays the interest income and capital gains coming from its customer base to these investors. In return, the counterparty (receiver) pays a variable interest rate to the bank and also bears any losses incurred in the loan.

Credit Risk of Derivatives

A vulnerable option is an option with default risk. The option holder receives the promised payment only if the counterparty is able to make the payment. In the absence of default risk, the payoff of the option is:

$$ \text{Max}\left( \text{S}\left( \text{T} \right) -\text{X},0 \right) $$

Where:

S = Underlying asset’s price at expiration.

X = Exercise price.

The vulnerable option holder receives the promised payment only if the value of the counterparty at maturity, V(T), is greater than the required payment on the option. The payoff’s option is:

$$ \text{Max}\left[ \text{Min}\left( \text{V},\text{S}\left( \text{T} \right) -\text{K} \right) ,0 \right] $$

For options with credit risk, a derivative contract can be taken to eliminate the credit risk. Provided the price of the vulnerable option can be reliably estimated, the price of the credit derivative to be used as an insurance policy can be determined. The payoff of the option used to hedge the credit risk of a vulnerable option is given by:

$$ \text{Max}\left( \text{S-K},\text{O} \right) -\text{Max}\left[ \text{Min}\left( \text{V},\text{S}\left( \text{T} \right) -\text{K} \right) ,0 \right] $$

An alternate approach to evaluate a vulnerable option is to compute the probability of default and apply a recovery rate if default occurs. Let’s assume that the default can only occur at maturity with probability p. If default occurs, the holder stands to receive a fraction z of the value of the option (z is the recovery rate). In these circumstances, the value of the option today is:

$$ \left( 1-\text{p} \right) \text{c}+\text{pzc} $$

Where c is the value of the option without default risk.

Example: Computing the Value of a Vulnerable Option

A firm has a debt issue with a default probability of 20% and a recovery rate of 50%. Determine the value of the vulnerable option.

Solution

The value of the option today is:

$$\begin{align*} \left( 1-\text{p} \right) \text{c}+\text{pzc}& = \left( 1-0.2 \right)\text{c}+0.2\left(0.5\right)\text{c} \\ &=0.9\text{c} \end{align*}$$

Therefore, the vulnerable option is worth 90% of the value of the option that’s free of default risk.

Accounting for Credit Risk Exposure in Valuing a Swap

With swaps, there can be default risk with respect to both counterparties. Thanks to netting, however, only a net payment is made by one of the parties.

Consider the case where a market maker enters a swap with a risky credit. The risky credit receives a fixed amount F at maturity of the swap – the fixed leg of the swap – and pays S(T). S(T), for instance, could be a floating rate payment determined on some index value at some point after the swap’s inception.

Let V(T) be the value of the risky credit net of all the debt that is senior to the swap. In these circumstances, the market maker receives \(S(T) – F\) in the absence of default risk. This payment can be positive or negative depending on the direction of market movement.

• If the payment is negative, the market maker pays \(F – S(T)\) to the risky credit for sure.
• If the payment is positive, the market maker receives \(S(T) – F\) if that amount is less than V(T).

Example: Swap

Swap information

• Notional = $100,000.
• Market maker pays a fixed rate of 10%; risky credit pays a variable rate linked to LIBOR.

Case 1 – LIBOR = 8%; risky credit’s V(T) = $50,000

F, paid by market maker = $10,000, while S(T), paid by the risky credit = $8,000

The market maker receives \(S(T) – F\) in the absence of default risk.

$$ \text S(\text T) – \text F = -$2,000 $$

Therefore, the market maker pays $2,000

Case 2 – LIBOR = 12%; risky credit’s V(T) = $50,000

F, paid by market maker = $10,000, while S(T), paid by the risky credit = $12,000

Again, the market maker receives \(S(T) – F\) in the absence of default risk.

$$ \text S(\text T) – \text F = $2,000 $$

Therefore, the market maker receives $2,000

The pay off of the swap to the market maker can therefore be summarized as follows:

$$ -\text{Max}\left( \text{F-S},\text{O} \right) -\text{Max}\left[ \text{Min}\left( \text{S},\text{V}-\text{F} \right) ,0 \right] $$

Practice Questions

Question 1

The face value of a firm’s only zero-coupon debt maturing in one year is $108 million, and the price of a put with exercise price \(F\) is $7.1 million. Today, the value of the zero-coupon bond paying $1in a year’s time is $0.89. What is the firm’s debt value?

A. $96.12 million.

B. $100.90 million.

C. $101.68 million.

D. $89.02 million.

The correct answer is D.

The value of the debt is given by the formula:

$$ D\left( V,F,T,t \right) ={ P }_{ t }\left( T \right) F-p\left( V,F,T,t \right) $$

From the problem we have that:

\({ P }_{ t }\left( T \right)\)=$0.89.

\(p\left( V,F,T,t \right)\)=$7.1 million.

\(F\)=$108 million.

Therefore:

$$ \begin{align*}D\left( V,F,T,t \right) &=$0.89\times $\text{108 million}\times $\text{7.1 million}\\& =$\text{89.02 million} \end{align*}$$

Question 2

Assuming that the probability of default for a firm is 0.15 and the recovery rate is 13 percent, what is the value of the vulnerable call without default risk?

A. 86.67%.

B. 1.95%.

C. 15.38%.

D. 86.95%.

The correct answer is D.

Recall that the current value of the option is given by the formula:

$$ \left( 1-p \right) c+pzc $$

where:

\(p\) = 0.11.

\(z\)= 0.3.

\(c\) is the option’s value without default risk.

Therefore:

$$\begin{align*} \text{The vulnerable call}&=(1-0.15)c+0.15\times 0.13\times c=0.86c\\& =86\% \text{without default risk}\end{align*}$$

Question 3

Assume that the equity of Alonso Transports is valued at $31 million and the cumulative distribution function \(N\left( d \right) \) evaluated at \(d\) is 1.8. The face value of the firm’s only zero coupon bond maturing in \(T\) years is $103 million.Calculate the value of the firm if its volatility is 28% and price of a zero-coupon bond paying $1 in a year’s time is $0.89 while \(T – t\) is 3 years.

A. $200.63M.

B. $84.19M.

C. $156.37M.

D. $199.05M.

The correct answer is B.

Recall that when the formula of the value of equity is inverted, the value of the firm is given by the formula:

$$ V=\left( \frac { 1 }{ N\left( d \right) } \right) S\left( V,F,T,t \right) +{ p }_{ t }\left( T \right) F\left( \frac { N\left( d \right) -\sigma \sqrt { T-t } }{ N\left( d \right) } \right) $$

From the problem:

\(N\left( d \right) \)=1.985.

\(S\left( V,F,T,t \right)\)=$31 million.

\(\sigma \)=0.28.

\({ p }_{ t }\left( T \right)\)=$0.79.

\(F\)=$103 million.

Therefore:

$$ \begin{align*}V&=\left( \frac { 1 }{ 1.8 } \right) \times $\text{31 million}+0.89\times $\text{103 million}\left( \frac { 1.8-0.28\times \sqrt { 3 } }{ 1.8 } \right)\\ &=$\text{84.19 million}\end{align*} $$