CVA (Part A)

After completing this reading, you should be able to:

• Explain the motivation for and the challenges of pricing counterparty risk.
• Describe credit value adjustment (CVA).
• Calculate CVA and the CVA spread with no wrong-way risk, netting, or collateralization.
• Evaluate the impact of changes in the credit spread and recovery rate assumptions on CVA.
• Explain how netting can be incorporated into the CVA calculation.
• Define and calculate incremental CVA and marginal CVA and explain how to convert CVA into a running spread.
• Explain the impact of incorporating collateralization into the CVA calculation.
• Describe debt value adjustment (DVA) and bilateral CVA (BCVA).
• Calculate BCVA and BCVA spread.

The Motivation for and the Challenges of Pricing Counterparty Risk

Valuation of counterparty risk refers to the practice of attaching a value to the risk of all outstanding positions with a given counterparty. For instance, let’s assume that a trader is planning to engage in an interest rate swap with a double-A counterparty whose outstanding debt is priced at a credit spread of 150 basis points per year. Assume that the notional value of the swap is $500 million.

In these circumstances, the trader will want to ensure that they settle for a rate that takes counterparty risk into account, i.e., the possibility that the counterparty will default on contractual payments once the swap is underway. To put a price tag on this risk, the trader will have to consider the following:

• Any existing trade the trader already has with the counterparty that may increase or even reduce the risk of the new trade (thanks to netting).
• Any collateral agreement that the trader could negotiate with the counterparty that may reduce risk.
• There may be ways to hedge the default of the counterparty since it has debt trading in the market.

In general, there are two key components needed to price counterparty risk:

1. The credit exposure, which is influenced by (I) any existing contracts and (II) risk mitigants such as netting and collateral.
2. The default probability of the counterparty.

Why is Pricing Counterparty Risk Important?

• Correct pricing of counterparty risk helps to ensure that earnings information put out by a firm is accurate.
• Pricing data can be used by trading desks and businesses to decide which trades to pursue and which ones to turn down. A trade is considered viable and economically feasible if its profit is greater than its cost.

When pricing counterparty risk, best practice calls for clear and well-organized responsibilities where the person or office tasked with the calculation process is specified.

Pricing counterparty risk (derivative contracts), however, is a difficult endeavor, particularly when compared to the pricing of bonds. With bonds, payments are made in only one direction once the investment has been made at the onset of the contract, and a default charge can easily be incorporated when discounting scheduled cashflows. With derivatives, contracts are bilateral, with payments often being made in both directions at specified times during the life of the contract. In addition, cash flows may be fixed, floating, or contingent.

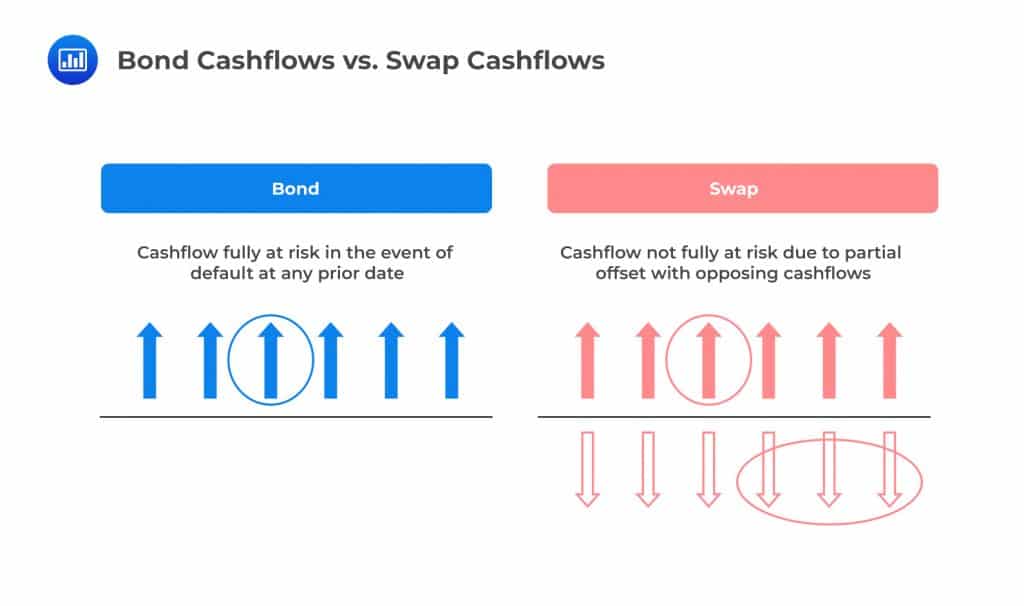
The figure below helps to visualize the problem with derivatives. Looking at bonds, a given cash flow is fully at risk (there’s a chance all of it will be lost) in the event of a default. In the swap case, only a fraction of the cash flow will be at risk because there’s an opposing cash flow that offsets the outflow to some degree. Although the risk on the swap is clearly smaller due to this effect, it is hard to determine the fraction of the swap cashflows that are indeed at risk. The amount at risk will depend on many factors, including forward rates and volatilities.

Credit Value Adjustment (CVA)

Credit valuation adjustment, CVA, is a change to the market value of derivative instruments to account for counterparty credit risk. It can also be interpreted as the expected value or price of counterparty risk.

Mathematically, CVA is the difference between the risk-free value and the true portfolio or position value that takes the possibility of a counterparty’s default into account.

$$ \text{Risky value} = \text{Risk-free value} – \text{CVA} $$

The equation above implies that it is possible to separate responsibilities in an institution and have a desk responsible for risk-free valuation and another one to determine the risky (counterparty) component. A swap trader, for example, can take on the task of pricing a swap as if it were risk-free and then rely on someone else in the office to determine the counterparty risk charge.

CVA Formula (In the Absence of Wrong-way Risk)

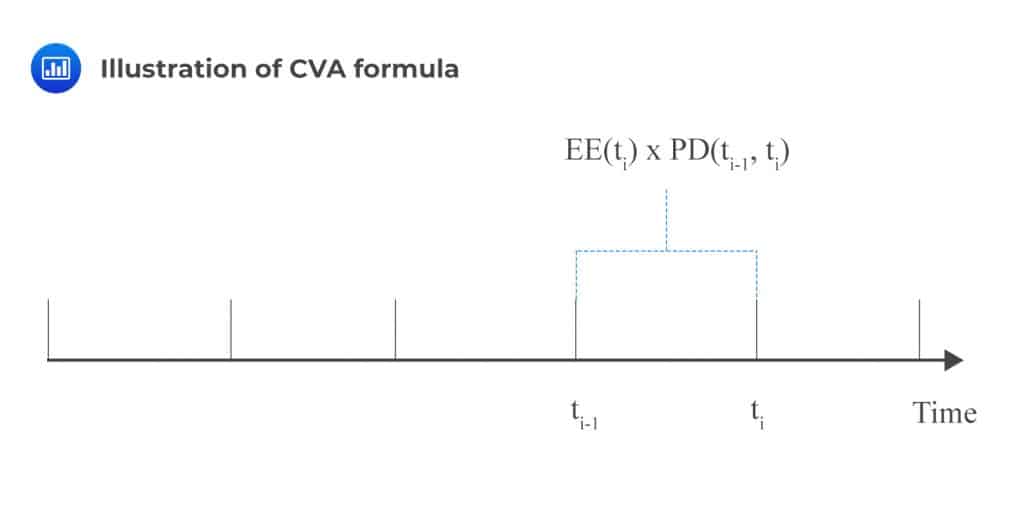
Ignoring wrong-way risk implies that we assume independence between default probability, exposure and recovery values. Under such assumptions, the CFA is calculated as follows:

$$ \text{CVA}=-\text{LGD}\sum _{ \text{i}=1 }^{ \text{m} }{ \text{EE}\left( { \text{t} }_{ \text{i} } \right) } \times \text{PD}\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right) $$

Where:

• Loss given default, LGD, is the percentage amount of the exposure expected to be lost in the event that the counterparty defaults (Recall that LGD = 1 – recovery rate).
• Expected exposure is the discounted expected exposure for all relevant future dates \({ \text{t} }_{ \text{i} }\).
• Default probability, PD, is the marginal probability of default between dates \({ \text{t} }_{ \text{i}-1 }\) and \({ \text{t} }_{ \text{i} }\).

The expected exposure and default probability are computed for each time period \(\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right)\)

The assumption that there’s no wrong-way risk means that the three components, as well as discount factors, can be calculated by different departments within an institution.

CVA as a Spread

Instead of calculating the CVA as a stand-alone value, we can also express it as a spread (annual charge). To do so, we divide the CVA by the unit premium of a risky annuity value for the maturity in question. This yields an annual spread expressed in basis points. The spread would effectively be a charge to the weaker counterparty. Assuming that the EE is constant over time and equal to its average value, EPE, CVA as a running spread is computed as follows:

$$ \cfrac { \text{CVA}\left( \text{t},\text{T} \right) }{ { \text{CDS} }_{ \text{premium} }\left( \text{t},\text{T} \right) } =-\text{EPE}\times { \text{X} }^{ \text{CDS} } $$

Where:

\({ { \text{CDS} }_{ \text{premium} }\left( \text{t},\text{T} \right) }\) = Unit premium value of a CDS (risky annuity)

\({ \text{X} }^{ \text{CDS} }\) = CDS premium that corresponds to the maturity date T (credit spread)

The left-hand side of the equation above represents CVA as a running spread.

It is important to emphasize the assumptions we have made so as to estimate CVA as a running spread:

• EPE is constant until maturity.
• Probability of default is constant until maturity.
• Both the EE and PD are symmetric over the entire profile.

Example: CVA as a Running Spread

An interest rate swap trading desk wishes to come up with a quick estimate of the CVA spread on a swap. According to the department tasked with calculating counterparty exposure, the EPE stands at 6%. A CDS with the counterparty as the reference entity attracts a premium of approximately 200 basis points per year. Determine the CVA as a running spread.

Solution

The CVA as a running spread is computed as follows:

$$ \cfrac { \text{CVA}\left( \text{t},\text{T} \right) }{ { \text{CDS} }_{ \text{premium} }\left( \text{t},\text{T} \right) } =-\text{EPE}\times { \text{X} }^{ \text{CDS} }=-6\%\times 2\%=-0.12\%=-12 \text{ basis points} $$

Having determined the CVA as a spread, the trading desk can now estimate the P&L impact of this. They can do so by pricing the same swap but paying 12 bps more on the pay leg (or receiving 12 bps less on the receive leg). The other option would be to either add or subtract a CVA charge of 12 basis points to one leg of the trade.

The Impact of Changes in the Credit Spread and Recovery Rate Assumptions on CVA

CVA is impacted by each of the following:

1. Credit spread levels.
2. Overall shape of the credit curve.
3. Recovery rate.
4. Basis risk arising from LGD assumptions.

Impact of Credit Spread

As the credit spread of the counterparty increases, the CVA increases (becomes less negative). However, the impact is not linear because default probabilities are limited to 100%. When the credit quality of the counterparty decreases, the CVA decreases (becomes more negative). If the counterparty is very close to default, the CVA tends to increase again (become less negative).

In default, the CVA falls to zero.

$$ \begin{align*} \textbf{Figure 3 –} & \textbf{CVA as a function of the credit spread of the counterparty (Forward} \\ & \textbf{contract-type exposure)} \end{align*} $$

$$ \begin{array}{c|c} \textbf{Spread (bps)} & \textbf{CVA} \\ \hline {150} & {-1,074} \\ \hline {300} & {-1,999} \\ \hline {600} & {-3,471} \\ \hline {1,200} & {-5,308} \\ \hline {2,400} & {-6,506} \\ \hline {4,800} & {-6,108} \\ \hline {9,600} & {-4,873} \\ \hline \text{Default} & {0} \\ \end{array} $$

Credit: The xVA Challenge Counterparty Credit Risk, Funding, Collateral, and Capital by Jon Gregory

Shape of the Credit Spread Curve

• With an upward sloping curve, defaults are back-loaded.
• With a downward sloping curve, defaults are front-loaded.
• With a flat curve, defaults are evenly spaced until maturity.

As a result, the CVA will be lower (more negative) for an upward-sloping curve compared to flat and downward-sloping curves. It is highest (least negative) with a downward sloping curve.

Recovery Rate

An increase in the recovery rate increases the implied probability of default but reduces the CVA. A related point has much to do with recovery timing: Whereas CDSs are settled quickly, either by way of a CDS auction cash settlement mechanism or the sale of the debt security in the market, following a default event, bilateral OTC derivatives take time to settle. That’s because the underlying transactions, such as netting (less collateral), are often quite difficult to define given a large number of trades.

This gives rise to two types of recovery: settled and actual recovery.

• Settled recovery refers to the recovery that could be achieved, following a credit event, by trading out of a claim, say, by selling a defaulted bond.
• Actual recovery is the recovery paid on a derivative at the conclusion of a bankruptcy or similar process.

Example

• A 20% recovery assumption for both settled and actual recovery rates will produce a lower (more negative) CVA compared to a 40% recovery assumption.
• However, a 10% settled recovery rate and a higher 40% actual recovered rate gives a much higher (less negative) CVA.

$$ \textbf{Figure 4 – CVA of the base case IRS for different recovery assumptions} $$

$$ \begin{array}{c|c} \textbf{Recovery (Settled/final)} & \textbf{CVA} \\ \hline \text{20% both} & {-2,072} \\ \hline \text{40% both} & {-1,999} \\ \hline \text{60% both} & {-1,862} \\ \hline \text{10%/40%} & {-1,398} \\ \end{array} $$

Incorporating Netting into CVA Calculations

As a risk mitigant, netting reduces CVA. A group of n transactions with the same counterparty under one netting agreement is called a netting set (NS). The CVA for a given netting set must be greater than or equal to the sum of stand-alone CVAs:

$$ CVA_{NS}≥\sum_{i=1}^{n}CVA_i $$

Fox example,

$$  -$8 \text{ million} ≥ -$10 \text{ million} $$

Therefore, one must evaluate the change in CVA before executing a trade.

A new trade should be priced so that its profit at least offsets any increase in CVA.

Mathematically,

$$ { \text{CVA} }_{ \text{i} }^{ \text{incremental} }={ \text{CVA} }_{ \text{NS}+\text{i} }-{ \text{CVA} }_{ \text{NS} } $$

The ability to calculate the incremental CVA helps the trading desk to attach a risk charge to every new trade brought in by a trader or sales person. That way, it is possible to come up with a compensation mechanism that is commensurate with the risk of the new trade.

The Impact of Incorporating Collateralization into the CVA Calculation

Collateral reduces CVA (results in a less negative CVA value) but it only changes the counterparty’s expected exposure, EE, not its PD.

Minimum transfer amounts increase CVA (result in a more negative CVA value) since they increase exposure linearly.

Incremental CVA

As noted earlier, incremental CVA is the change (or increment) in CVA that a new trade will create, taking netting into account.

It is derived as follows:

$$ { \text{CVA} }_{ \text{i} }^{ \text{incremental} }=-\text{LGD}\sum _{ \text{i}=1 }^{ \text{m} }{ { \text{EE} }_{ \text{i} }^{ \text{incremental} } } \left( { \text{t} }_{ \text{i} } \right) \times \text{PD}\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right) $$

If you look closely, you’ll notice that the incremental CVA looks pretty much like the original CVA. The only difference is that the original stand-alone EE is replaced by the incremental EE.

$$ { \text{CVA} }=-\text{LGD}\sum _{ \text{i}=1 }^{ \text{m} }{ { \text{EE} } \left( { \text{t} }_{ \text{i} } \right)} \times \text{PD}\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right) $$

The incremental EE is the change in EE at each point in time caused by the new trade, which impacts the original exposure.

Example: Incremental CVA

The table below gives the incremental CVA calculations for a seven-year USD swap paying fixed with respect to four different existing transactions and compared to the stand-alone value. We assume that the credit curve is flat at 300 bps with a 60% LGD.

$$ \textbf{Figure 5 – the incremental CVA calculations for a seven-year USD swap} $$

$$ \begin{array}{c|c} \textbf{Existing transaction} & \textbf{Incremental CVA} \\ \hline \text{None (stand-alone)} & {-0.4838} \\ \hline \text{Payer IRS USD 5Y} & {-0.4821} \\ \hline \text{Payer swaption USD 5*5Y} & {-0.4628} \\ \hline \text{xCCY USDJPY 5Y} & {-0.2532} \\ \hline \text{Receiver 1RS USD 5Y} & {-0.1683} \\ \end{array} $$

Observations

• The incremental CVA can never be lower (more negative) than the stand-alone CVA.
• The incremental CVA is only slightly reduced for a very similar existing trade (5-year IRS payer). This indicates a high positive correlation between the two trades.

Marginal CVA

Marginal CVA enables the trading desk to break down netted trades into trade-level contributions that sum to the total CVA. As an ex-post measure, it is determined after the portfolio CVA has been calculated and then allocated to trades.

In other words, the marginal CVA is found by breaking down the CVA for any number of transactions into transaction-level contributions that sum to the total CVA. The breakdown is carried out based on certain criteria.

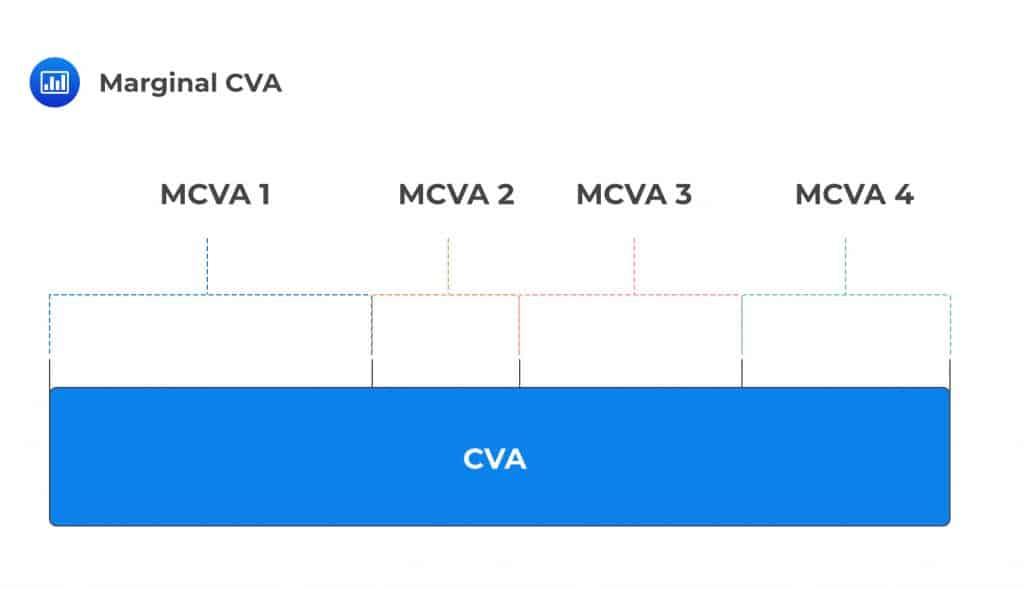The marginal CVA helps the trading desk to single out transactions that have the greatest impact on a counterparty’s CVA. The incremental CVA and marginal CVA can be the same, depending on the allocation criteria.

Debt Value Adjustment (DVA)

Up to this point, we have assumed that the party calculating the CVA (party with positive exposure) has a zero chance of default. In a transaction involving a counterparty and a large multinational financial institution, for example, such an assumption would appear fairly innocuous. Indeed, it falls in line with the “going-concern” accounting principle, where every transaction that appears on the financial statements is initiated upon the assumption that the business will remain in existence (solvent) for an indefinite period. That means that the financial institution is assumed to have zero counterparty risk from the perspective of the counterparty. However, the events of the 2007/09 financial crisis deconstructed and poked big holes in this assumption, seeing that several large institutions, previously considered financially invincible and too big to fail, went under.

As a result of the 2007/2009 happenings, international accountancy practices now recognize that all trades have bilateral counterparty risk. They allow large institutions to consider their own default in the valuation of their liabilities. This brings us to debt value adjustment.

Debt value adjustment, DVA, is the counterparty risk of the institution writing the contract. It can be thought of as the negative of CVA. In other words, an institution’s DVA is the counterparty’s CVA. DVA is actually a benefit to the defaulting institution. That’s because if the institution happens to default when its MTM exposure is negative, the institution will only pay the counterparty the recovery amount, which is just a fraction of what they owe. The difference between the amount recovered by the counterparty and the actual amount the institution owes is a gain to the institution.

While CVA considers only positive exposure, DVA considers only negative exposure.

Bilateral CVA

Bilateral CVA is CVA that incorporates an entity’s own credit risk into the derivative valuation process. It is built upon the acknowledgment that the creditworthiness of both parties in a bilateral contract matters. In a transaction between a small counterparty and a larger financial institution, an informed counterparty (viewed as the “underdog”) would be expected to adjust for the institution’s credit risk when valuing the transaction.

$$ \begin{align*} \text{BCVA} & = \text{CVA} + \text{DVA} \\ \text{CVA} & =-{ \text{LGD} }_{ \text{c} }\sum _{ \text{i}=1 }^{ \text{m} }{ \text{EE}\left( { \text{t} }_{ \text{i} } \right) } \times { \text{PD} }_{ \text{c} }\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right) \\ \text{DVA} & =-{ \text{LGD} }_{ \text{p} }\sum _{ \text{i}=1 }^{ \text{m} }{ \text{NEE}\left( { \text{t} }_{ \text{i} } \right) } \times { \text{PD} }_{ \text{p} }\left( { \text{t} }_{ \text{i}-1 },{ \text{t} }_{ \text{i} } \right) \end{align*} $$

Where:

NEE = Negative expected exposure (EE from the counterparty’s perspective).

P and C indicate the party making the calculation and their counterparty respectively.

BCVA as a Spread

We can rewrite BCVA in terms of the EPE and ENE as follows:

$$ \text{BCVA}=-{\text{EPE}}\times{\text{Spread}}_{\text{C}}-\text{ENE}\times{\text{Spread}}_{\text{P}} $$

If we assume that ENE is the opposite of EPE, then:

$$ \text{BCVA}\approx-{\text{EPE}}\times\left({\text{Spread}}_{\text{C}}-{\text{Spread}}_{\text{P}}\right) $$

Example: BCVA As a Running Spread

An interest rate swap trading desk wishes to come up with a quick estimate of the CVA spread on a swap.

$$ \text{Given: EPE} = 6\%; \text{ENE} = -4\%; {\text{Spread}}_{\text{C}} = 200 \text{bps}; {\text{Spread}}_{\text{p}} = 100 \text{bps} $$

From the perspective of the trading desk,

$$ \text{BCVA}=-6\%\times2\%-\left( -4\%\times 1\% \right) =-0.08\%=-8 \text{ bps} $$

Hence, the trading desk will charge the counterparty 8 bps for the overall counterparty risk.

Compared to the previous example, we can see that the BCVA is reduced from the (unilateral) CVA calculation of 12 bps.

Practice Question

Fenton Associates is a trading firm from Norway that needs to have a very quick idea on a swap’s bilateral credit value adjustment (\(BCVA\)). The firm knows that the expected positive exposure (\(EPE\)) for a trade of this type is 10.5% with an expected negative exposure (\(ENE\)) of -8.2%. The counterparty credit spread is found out to be around 150 bps and the credit spread of the trader’s own institution is 121 basis points per year. What is the \(BCVA\)?

A. 9.189.

B. -5.83.

C. -18.113.

D. -25.672.

The correct answer is B.

Recall that \(BCVA\), which is an obvious extension of \(CVA\) and \(DVA\), is calculated by using the following formula:

$$ BCVA=-EPE\times { Spread }_{ C }-ENE\times { Spread }_{ P } $$

From the question we have that:

\(EPE=0.105\).

\({ Spread }_{ C }=150\).

\(ENE=-0.082\).

\({ Spread }_{ P }=121\).

Therefore:

$$ \begin{align*}BCVA&=(-0.105\times 150)-(-0.082\times 121)\\ & = -5.83 \end{align*}$$