Nonstationary Time Series

After completing this reading, you should be able to:

• Describe linear and nonlinear time trends.
• Explain how to use regression analysis to model seasonality.
• Describe a random walk and a unit root.
• Explain the challenges of modeling time series containing unit-roots.
• Describe how to test if a time series contains a unit root.
• Explain how to construct an h-step-ahead point forecast for a time series with seasonality.
• Calculate the estimated trend value and form an interval forecast for a time series.

Recall that the stationary time series have means, variance, and autocovariance that are independent of time. Therefore any time series that violates this rule is termed as the non-stationary time series.

The nonstationary time series include time trends, random walks( also called unit-roots) and seasonalities. Time trends reflect the feature of the time series to grow over time.

Seasonalities occur due to change in the time series over different seasons such as each quarter. Seasonalities can be shifts of the mean (for example depending on the period of the year) and the mean cycle of the time series (this occurs when the shock of the current value depends on the shock of the same future period). Seasonalities can be modeled using the dummy variables or modeling it period after period changes (such as year after year) in an attempt to remove the seasonal change of the mean.

In a random walk, time series depends on each other and their respective shocks. We discuss each of the non-stationarities.

Time Trends.

The time trend deterministically shifts the mean of the time series. The time trend can be linear and non-linear (which includes log and quadratic time series).

Linear Time Trends

Linear trend models are those that the dependent variable changes at a constant rate with time. If the time series \(\text y_{\text t}\) has a linear trend, we can model the series by the following equation:

$$ \text Y_{\text t}=\beta_0+\beta_1 t+\epsilon_{\text t},{\text t}=1,2,…,{\text T} $$

Where

\(\text Y_{\text t}\) =the value of the time series at time t (trend value at time t)

\(\beta_0\)=the y-intercept term

\(\beta_1\)=the slope coefficient

t=time, the independent (explanatory) variable

\(\epsilon_{\text t}\)= a random error term (Shock) and is white noise \((\epsilon_{\text t}\sim \text{WN}(0,\sigma^2))\)

From the equation above, the \(\beta_0+\beta_1 {\text t}\) predicts \(\text y_{\text t}\) at any time t. The slope \(\beta_1\) is described as the trend coefficient since it is the slope coefficient. We estimate both factors \(\beta_0\) and \(\beta_1\) using the ordinary least squares and denoted as: \(\hat \beta_0\) and \(\hat \beta_1\) respectively.

The mean of the linear time series is:

$$ \text E (\text Y_{\text t})=\beta_0+\beta_1 {\text t} $$

On a graph, a linear trend appears as a straight line angled diagonally up or down.

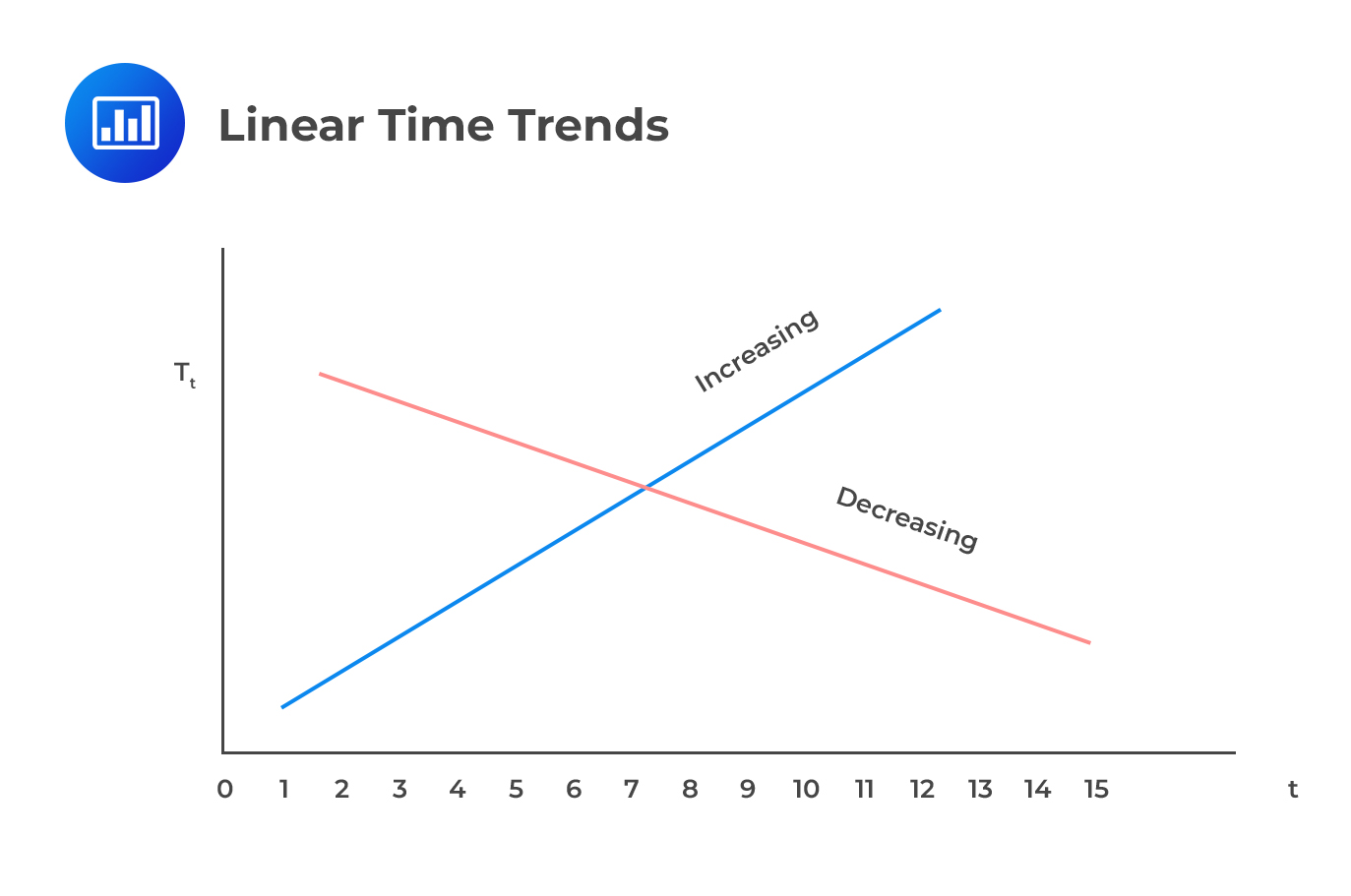Estimation of the Trend Value Under Linear Trend Models

Using the estimated coefficients, we can predict the value of the dependent variable at any time (t=1, 2…, T). For instance, the trend value at time 2 is \(\hat {\text Y}_2=\hat \beta_0+\hat \beta_1\) (2). We can also forecast the value of the time series outside the sample’s period, that is, T+1. Therefore, the predicted value of \(\text Y_{\text t}\) at time T+1 is \(\hat {\text Y}_{\text T+1}=\hat \beta_0+\hat \beta_1 (\text T+1)\).

Example: Calculating the Trend Value

A linear trend is defined to be \(\text Y_{\text t}=17.5+0.65{\text t}\). What is the trend projection for time 10?

Solution

We substitute t=10, which is:

$$ \text T = 17.5 + 0.65×10 = 24 $$

Disadvantages of Linear Time Series

In linear time series, the growth is a constant which might pose problems in economic and financial time series.

1. When the trend is positive, then the growth rate is expected to decrease over time.
2. If the slope coefficient is less than 0, the \(\text Y_{\text t}\) will tend toward negative values, a situation that would not be plausible in most financial time series, e.g., asset prices and quantiles.

Considering these limitations, we discuss the log-linear time series, with a constant growth rate rather than just a constant rate.

Log-Linear Trend Models

Sometimes the linear trend models result in uncorrelated errors. For instance, the time series with exponential growth rates. The appropriate model for the time series with exponential growth is the Log-linear trend model.

Log-linear trends are those in which the variable changes at an increasing or decreasing rate rather than at a constant rate like in linear trends.

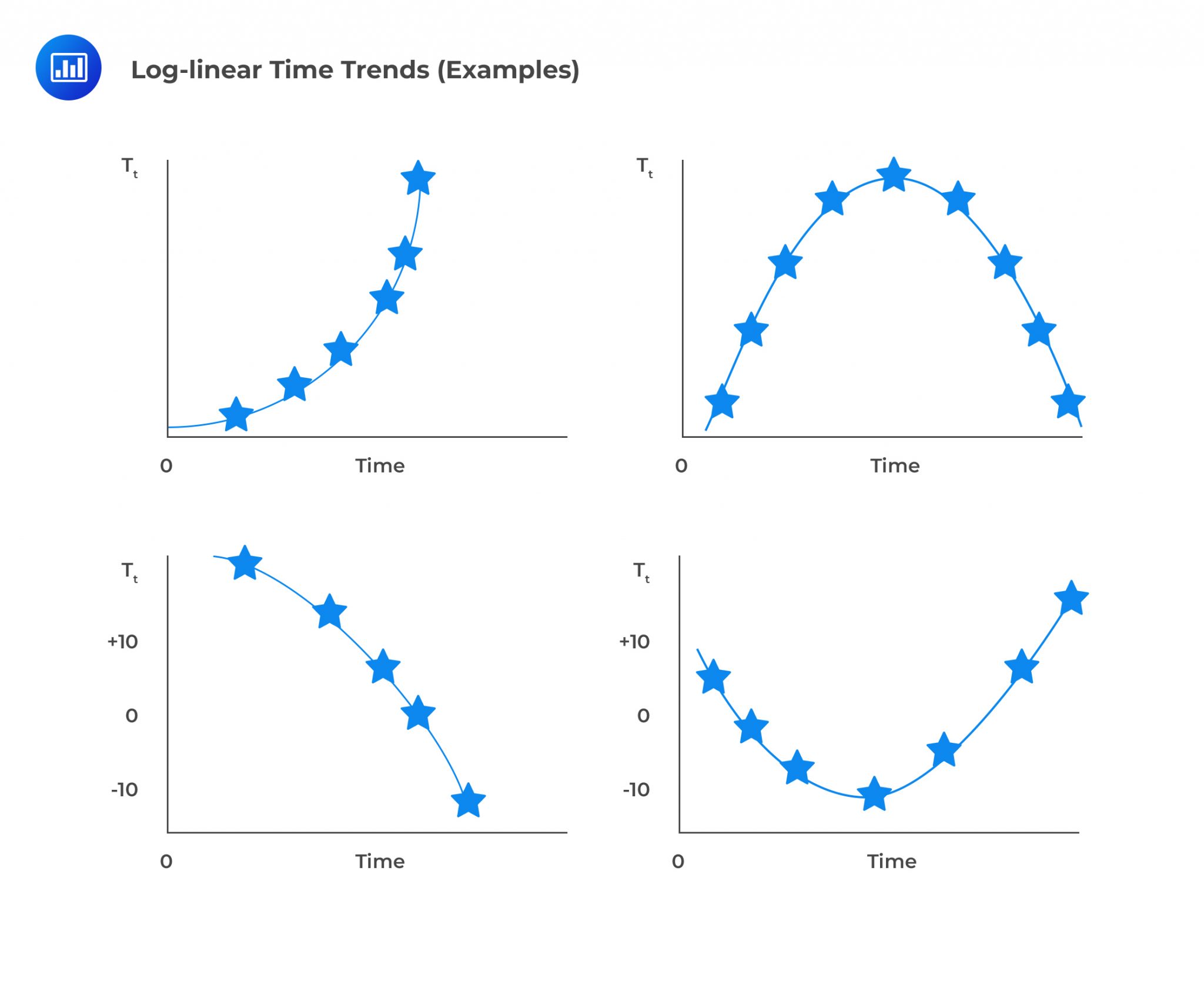Assume that the time series is defined as:

$$ {\text Y_{\text t}}={\text e}^{\beta_0+\beta_1 \text t},\text t=1,2,…,{\text T} $$

Which also can be written as (by taking the natural logarithms on both sides):

$$ {\text {ln }} {\text Y_{\text t}} ={\beta_0+\beta_1 \text t},\quad \text t=1,2,…,{\text T} $$

By Exponential rate, we mean growth at a constant rate with continuous compounding. This can be seen as follows: Using the time series formula above, the value of the time series at time 1 and 2 are \(\text y_1={\text e}^{\beta_0+\beta_1 (1)}\) and \(\text y_2={\text e}^{\beta_0+\beta_1 (2)}\) . The ratio \(\frac {\text y_2}{\text y_1}\) is given by:

$$ \cfrac {\text Y_2}{\text Y_1} =\cfrac {{\text e}^{\beta_0+\beta_1 (2)}}{{\text e}^{\beta_0+\beta_1 (1)}} ={\text e^{\beta(1)}} $$

Similarly, the value of the time-series at time t is \({\text Y_{\text t}}={\text e}^{\beta_0+\beta_1 \text t}\), and at t+1, we have \(\text Y_{\text t+1}={\text e}^{\beta_0+\beta_1 (\text t+1)}\). This implies that the ratio:

$$ \cfrac {\text Y_{\text t+1}}{\text Y_{\text t}} =\cfrac {{\text e}^{\beta_0+\beta_1 (\text t+1)}}{{\text e}^{\beta_0+\beta_1 (\text t)} }=\text e^{\beta_1} $$

If we take the natural logarithm on both sides of the above equation we have:

$$ \text {ln}\left(\cfrac {\text Y_{\text t+1}}{\text Y_{\text t}} \right)=\text {ln⁡} {\text Y_{\text t+1}}-\text {ln⁡} {\text Y_{\text t}}=\beta_1 $$

The log-linear model implies that:

$$ \text E(\text{ln⁡ }{\text Y_{\text t+1}}-\text {ln⁡} {\text Y_{\text t}})=\beta_1 $$

From the above results, proportional growth in time series over the two consecutive periods is equal. That is:

$$ \cfrac {{\text y_{\text t+1}}-{\text y_{\text t}}}{{\text y_{\text t}}} =\cfrac {{\text y_{\text t+1}}}{{\text y_{\text t}}} -1=\text e^{\beta_1 }-1 $$

Example: Calculating the Trend Value of a Log-Linear Trend Time Series

An investment analyst wants to fit the weekly sales (in millions) of his company by using the sales data from Jan 2016 to Feb 2018. The regression equation is defined as:

$$ \text {ln⁡} {\text Y_{\text t}} =5.1062 +0.0443{\text t},\text t = 1,2,…,100 $$

What is the trend estimated value of the sales in the 80th week?

Solution

From the regression equation, \(\hat \beta_0=5.1062\) and \(\hat \beta_1=0.0443\). We know that, under log-linear trend models, the predicted trend value is given by:

$$ {\text Y_{\text t}}={\text e}^{\hat \beta_0+\hat \beta_1 {\text t}} $$

$$ \Rightarrow {\text Y}_{80}={\text e}^{5.1062 +0.0443×80}=5711.29 {\text { Million}} $$

Quadratic Time Trend

A polynomial-time trend can be defined as:

$$ {\text Y_{\text t}}=\beta_0+\beta_1 \text t+\beta_2 {\text t}^2+⋯+\beta_{\text m} {\text t}^{\text m} \epsilon_{\text t},\text t=1,2,…,\text T $$

Practically speaking, the polynomial-time trends are only limited to the linear (discussed above) and the quadratic (second degree) time trend. In a quadratic time trend, the parameter can be estimated using the OLS. The approximated parameter are asymptotically normally distributed and hence statistical inference using the t-statistics and the standard error happen only if the residuals \(\epsilon_\text t\) are white noise.

The Log-Quadratic Time Trend

As the name suggests, this time trend is a mixture of the log-linear and quadratic time series. It is given by:

$$ \text {ln }⁡{\text Y_{\text t}}=\beta_0+\beta_1 \text t+\beta_2 {\text t}^2 $$

It can be shown that the growth rate of the log-quadratic time trend is \(\beta_1+2\beta_2 {\text t}\). This can be seen as follows:

The value of the time-series at time t is \(⁡{\text Y_{\text t}}={\text e}^{\beta_0+\beta_1 \text t+\beta_2 {\text t}^2}\), and at t+1, we have

\(\text Y_{\text t+1}={\text e}^{\beta_0+\beta_1 (\text t+1)+\beta_2 {(\text t+1)}^2}\). This implies that the ratio:

$$ \cfrac { \text Y_{\text t+1}}{\text Y_{\text t}} =\cfrac {{\text e}^{\beta_0+\beta_1 (\text t+1)+\beta_2 {(\text t+1)}^2}}{{\text e}^{\beta_0+\beta_1 \text t+\beta_2 {\text t}^2}}=\text e^{\beta_1+2\beta_2 {\text t}} $$

If we take a natural log on the results, we get the desired result.

Example: Calculating the Growth Rate of Log-Quadratic Time Trend

The monthly real GDP of a country over 20 years can be modeled by the time series equation given by:

$$ \text {RG}_{\text T}=6.75+0.015{\text t}+0.0000564{\text t}^2$$

What is the growth rate of the real GDP of this country at the end of 20 years?

Solution

This is the log-quadratic time trend whose growth rate is given by

$$ {\beta_1+2\beta_2 {\text t}} $$

From the regression time-series equation given, we have \({\hat \beta}_1=0.015\) and \({\hat \beta}_2=0.0000564\) so that the growth rate is given by:

$$ {\beta_1+2\beta_2 {\text t}}=0.015+2×0.0000564×240=0.0421$$

Note that, since the data is modeled monthly, at the end of 20 years implies 240th month!

The coefficient of variation \((\text R^2)\) for the time trend series is always high and will tend to 100% as the sample size increases. Therefore, the coefficient of variation is not an appropriate measure in trend series. Other alternatives such as residual diagnostics, can be useful.

Seasonality

Seasonality is a feature of a time series in which the data undergoes regular and predictable changes that recur every calendar year. For instance, gas consumption in the US rises during the winter and falls during the summer.

Seasonal effects are observed within a calendar year, e.g., spikes in sales over Christmas, while cyclical effects span time periods shorter or longer than one calendar year, e.g., spikes in sales due to low unemployment rates.

Modeling Seasonal Time Series

Regression on seasonal dummies is an essential method of modeling seasonality. Assuming that there are s seasons in a year. Then the pure annual dummy model is:

$$ \begin{align*} \text Y_{\text t} & =\beta_0+\gamma_1 {\text D}_{1{\text t}}\gamma_2 \text D_{2 \text t}+⋯+\gamma_{\text s-1} {\text D}_{{\text s-1 \text t}}+\epsilon_{\text t} \\ &=\beta_0+\sum_{\text j=1}^{\text s-1} {\gamma_{\text j} \text D_{\text {jt}} } +\epsilon_{\text t} \\ \end{align*} $$

\(\text D_{\text {jt}}\) is defined as:

$$ \text D_{\text {jt}}=\begin{cases} 1, \text{t mod s}=j \\ 0, \text{t mod s}\neq j \end{cases} $$

\(\gamma_{\text j}\) measures the amount of difference of the mean at period j and s.

Note X mod Y is the remainder of the X/Y.For instance, 9 mod 4=1.

The mean of the first period of the seasonality is:

$$ \text E[\text Y_1 ]=\beta_0+\gamma_1 $$

And the mean of period 2 is:

$$ \text E[\text Y_2 ]=\beta_0+\gamma_2 $$

Since period s, all dummy variables are zero, then the mean of the seasonality at time s is:

$$ \text E[\text Y_{\text s} ]=\beta_0 $$

The parameters of seasonality are estimated using the OLS estimators by regressing \(\text Y_{\text t}\) on constant and s-1 dummy variables.

Combination of Stationary and Non-Stationary Time Series

Time trends and seasonalities can be insufficient in explaining economic time series and since their residuals might not be white noise. In the case that the non-stationary time series appears to be stationary, but the residuals are not white noise, we can add stationary time series components (such as AR and MA) to reflect the components of the non-stationary time series.

Consider the following linear time trend.

$$ \text Y_{\text t}=\beta_0+\beta_1 {\text t}+\epsilon_{\text t} $$

If the residuals are not white noise but the time series appears to be stationary, we can include an AR term to make the model’s residuals white noise:

$$ \text Y_{\text t}=\beta_0+\beta_1 {\text t}+\delta_1 \text Y_{\text t-1}+\epsilon_{\text t} $$

We can also add the seasonal component (if it exists):

$$ \text Y_{\text t}=\beta_0+\beta_1 {\text t}+\sum_{\text j=1}^{\text s-1} \gamma_{\text j} \text D_{\text {jt}}+\delta_1 \text Y_{\text t-1}+\epsilon_{\text t} $$

Note that the AR component reflects the cyclicity of the time series, \(\gamma_{\text j} \) measures the shifts of the mean from the trend growth, i.e \(\beta_1 {\text t}\). However, combinations of the time series do not always lead to a model with the required dynamics. For instance, the Ljung-Box statistics may suggest rejection of the null hypothesis.

Unit Roots and Random Walks

A random walk is a time series in which the value of the series in one period is equivalent to the value of the series in the previous period plus the unforeseeable random error. A random walk can be defined as follows:

Let

$$\text Y_{\text t}=\text Y_{\text t-1}+\epsilon_{\text t}$$

Intuitively,

 $$\text Y_{\text t-1}=\text Y_{\text t-2}+\epsilon_{\text t-1}$$

If we substitute \(\text Y_{\text t-1}\) in the first equation, we get,

$$ \text Y_{\text t}=(\text Y_{\text t-2}+\epsilon_{\text t-1})+\epsilon_{\text t} $$

Continuing this process, it implies that a random walk is given by:

$$ \text Y_{\text t}=\text Y_0+\sum_{\text i=1}^{\text t} \epsilon_{\text i} $$

The random walk equation is a particular case of an AR(1) model with \(\beta_0=0\) and \(\beta_1=1\). Thus, we cannot utilize the regression techniques to estimate such AR(1). This is because a random walk does not have a finite mean-reverting level or finite variance. Recall that if \(\text Y_{\text t}\) has a mean-reverting level, then \(\text Y_{\text t}=\beta_0+\beta_1 {\text Y}_{\text t}\) and thus \(\frac {\beta_0}{1-\beta_1}\). However, in a random walk, \(\beta_0=0\) and \(\beta_1=1\) so, \(\frac {0}{1-1}=0\).

The variance of a random walk is given by:

$$ \text V(\text Y_{\text t} )=\text t \sigma^2 $$

The implication of the infinite variance of a random walk is that we are unable to use standard regression analysis on a time series that appears to be a random walk.

Unit Roots

We have been discussing the random walks without a drift; that the current value is the best predictor of the time series in the next period.

A random walk with a drift is defined as a time-series where it increases or decreases by a constant amount in each period. It is mathematically described as:

$$ \text Y_{\text t}=\beta_{0}+\beta_{1} {\text Y}_{\text t-1}+\epsilon_{\text t}$$

\( \beta_0\neq 1,\beta_1=1 \)

Or

$$\text Y_{\text t}=\beta_0+{\text Y}_{\text t-1}+\epsilon_{\text t}$$

Where \(\epsilon_{\text t} \sim \text{WN}(0,\sigma^2) \)

Recall that \(\beta_1=1\) implies undefined mean-reversion level and hence non-stationarity. Therefore, we are unable to use the AR model to analyze a time series unless we transform the time series by taking the first difference we get:

$$ \Delta\text Y_{\text t}=\text Y_{\text t}-\text Y_{(\text t-1)},y_t=\beta_0+\epsilon_{\text t},\forall \beta_0\neq 0 $$

Which is covariance stationary.

The unit root test involves the application of the random walk concepts to determine whether a time series is nonstationary by focusing on the slope coefficient in a random walk time series with a drift case of AR(1) model. This test is popularly known as the Dickey-Fuller Test

The Unit Root Problem

Consider an AR(1) model. If the time-series originates from an AR(1) model, then the time-series is covariance stationary if the absolute value of the lag coefficient \(\beta_1\) is less than 1. That is, \(|\beta_1 | < 1\). Therefore, we could not depend on the statistical results if the lag coefficient is greater or equal to 1 (\(|\beta_1 | \ge 1\)).

When the lag coefficient is precisely equal to 1, then the time series is said to have a unit root. In other words, the time-series is a random walk and hence not covariance stationary.

The unit root problem can also be expressed using the lag polynomial. Let

\(\psi (\text L)\) be the full lag polynomial, which can be factorized into the unit root lag denoted by (1-L) and the remainder lag polynomial \(\phi (\text L\)) which is the characteristic lag for stationary time series. Moreover, let \(\theta(\text L) \epsilon_{\text t}\) be an MA. Thus, the unit root process can be described as:

$$ \psi(\text L) \text Y_{\text t}=\theta( \text L) \epsilon_{\text t} $$

This can be factorized into:

$$ (1-\text L)\phi (\text L)=\theta (\text L) \epsilon_{\text t} $$

Example: Checking for Unit Roots using the Lag Polynomials

An AR(2) model is given by \(\text Y_{\text t}=1.7{\text Y}_{\text t-1}-0.7\text Y_{\text t-2}+\epsilon_{\text t}\). Does the process contain a unit root?

Solution

If we rearrange the equation:

$$ \text Y_{\text t}-1.7{\text Y}_{\text t-1}+0.7\text Y_{\text t-2}=\epsilon_{\text t} $$

Using the definition of a lag polynomial, we can write the above equation as:

$$ (1-1.7{\text L}+0.7{\text L}^2)Y_t=\epsilon_{\text t} $$

The right-hand side is a quadratic equation which can be factorized. So,

$$ (1-\text L)(1-0.7\text L)Y_t=\epsilon_{\text t} $$

Therefore, the process has a unit root due to the presence of a unit root lag operator (1-L).

Challenges of Modeling Time Series Containing Unit Roots

1. A unit root process does not have a mean-reverting level. Recall that the stationary time series does mean revert, that is, the long-run mean can be estimated.
2. In a time series with a unit root, spotting spurious relationships is a problem. A spurious correlation is where there is no important link between the time series but regression analysis produces significant parameter estimates.
3. The parameter estimators in ARMA time series with a unit root possess Dickey-Fuller (DF) distribution, which is asymmetric, dependent on the sample size, and that its critical value depends on whether time trends have been incorporated. This characteristic makes it difficult to come up with sound statistical inference and model selection when fitting the models.

Transformation of Time Series with Unit Roots

If the time series seem to have unit roots, the best method is to model it using the first-differencing series as an autoregressive time series, which can be effectively analyzed using regression analysis.

Recall that the time series with a drift is a form of AR(1) model given by:

$$ \text y_{\text t}=\beta_0+{\text Y}_{\text t-1}+\epsilon_{\text t} ,$$

Where \(\epsilon_{\text t}\sim \text{WN}(0,\sigma^2)\)

Clearly \(\beta_1=1\) implies that the time series has an undefined mean-reversion level and hence non-stationary. Therefore, we are unable to use the AR model to analyze time series unless we transform the time series by taking the first difference to get:

$$ \text Y_{\text t}=\text Y_{\text t}-\text Y_{(\text t-1)} \Rightarrow \text y_{\text t}=\beta_0+\epsilon_{\text t},\forall \beta_0 \neq 0 $$

Where the \(\epsilon_{\text t}\sim \text{WN}(0,\sigma^2)\) and thus covariance stationary.

Using the lag polynomials, let \(\Delta \text Y_{\text t}=\text Y_{\text t}-\text Y_{(\text t-1)}\) where \(\text Y_{\text t}\) has a unit root (implying that \(\text Y_{\text t}-\text Y_{(\text t-1)}\) does not have a unit root.), then:

$$ \begin{align*} (1-\text L)\phi(\text L) \text Y_{\text t} &=\epsilon_{\text t} \\ \phi(\text L)[(1-\text L) \text Y_{\text t}]&=\epsilon_{\text t} \\ \phi(\text L)[(\text Y_{\text t}-\text L \text Y_{\text t} )]&=\epsilon_{\text t} \\ \phi(\text L) \Delta \text Y_{\text t} &=\epsilon_{\text t} \\ \end{align*}$$

Since the lag polynomial \(\phi(\text L)\) is stationary series lag polynomial, the time series defined by \(\Delta \text Y_{\text t}\) must be stationary.

Unit Root Test

The unit root test is done using the Augmented Dickey-Fuller (ADF) test. The test involves OLS estimation of the parameters where the difference of the time series is regressed on the lagged level, appropriate deterministic terms, and the lagged difference.

The ADF regression is given by:

$$ \Delta {\text Y}_{\text t}=\gamma {\text Y}_{\text t-1}+(\delta_0+\delta_1 \text t)+(\lambda \Delta {\text Y}_{\text t-1}+\lambda_2 \Delta {\text Y}_{\text t-2}+⋯+\lambda_{\text p} \Delta \text Y_{(\text t-\text p)}) $$

Where:

\(\gamma {\text Y}_{\text t-1}\)=Lagged level

\(\delta_0+\delta_1 \text t\)=deterministic terms

\(\lambda \Delta {\text Y}_{\text t-1}+\lambda_2 \Delta {\text Y}_{\text t-2}+⋯+\lambda_{\text p} \Delta \text Y_{(\text t-\text p)}\)=Lagged differences.

The test statistic for the ADF test is that of \(\hat \gamma (\text{estimate of } \gamma)\).

To get the gist of this, assume that we are conducting an ADF test on a time series with lagged level only:

$$ \Delta \text Y_{\text t}=\gamma \text Y_{\text t-1} $$

Intuitively, if the time series is a random walk, then:

$$ \text Y_{\text t}=\text Y_{\text t-1}+\epsilon_{\text t} $$

If we subtract \(\text Y_{\text t-1}\) on both sides we get:

$$ \begin{align*} \text Y_{\text t}-\text Y_{\text t-1}&=\text Y_{\text t-1}-\text Y_{\text t-1}+\epsilon_{\text t} \\ \Rightarrow \Delta {\text Y}_{\text t}&=0×\text Y_{\text t-1}+\epsilon_{\text t} \\ \end{align*} $$

Therefore, it implies that the time series is a random walk if γ=0. This leads us to the hypothesis statement of the ADF test:

\(\text H_0:\gamma=0\) (The time series is a random walk)

\(\text H_1:\gamma < 0\) (the time series is a covariance stationary )

You should note this is a one-sided test, and thus, the null hypothesis is not rejected if γ>0. The positivity of γ corresponds to an AR time series stationary. For example, recall that the AR(1) model is given by:

$$ \text Y_{\text t}=\beta_0+\beta_1 \text Y_{\text t-1}+\epsilon_{\text t} $$

If we subtract \(\text Y_{\text t-1}\) from both sides of the AR(1) above we have:

$$ \text Y_{\text t}-\text Y_{\text t-1}=\beta_0+(\beta_1-1) \text Y_{\text t-1}+\epsilon_{\text t} $$

Now let \(\gamma=(\beta_1-1)\). Therefore,

$$ \Delta \text Y_{\text t}=\beta_0+\gamma \text Y_{\text t-1}+\epsilon_{\text t} $$

Clearly, if \(\beta_1=1\), then let \(\gamma=0\). Therefore, \(\gamma=0\) is the test for \(\beta_1=1\). In other words, if there is a unit root in an AR(1) model (with the dependent variable being the difference between the time series and independent variable of the first lag) then, \(\gamma=0\), implying that the series has a unit root and is nonstationary.

Implementing an ADF test on a time series requires making two choices: which deterministic terms to include and the number of lags of the differenced data to use. The number of lags to include is simple to determine—it should be large enough to absorb any short-run dynamics in the difference \(\Delta \text Y_{\text t}\)

The appropriate method of selecting the lagged differences is the AIC (which selects a relatively larger model as compared to BIC). The length of the lag should be set depending on the length of the time series and the frequency of the sampling.

The Dickey-Fuller distributions are dependent on the choice of deterministic terms included. The deterministic terms can be excluded, and instead, use constant terms or trend deterministic terms. While keeping all other things equal, the addition of more deterministic terms reduces the chance of rejecting the null hypothesis when the time series does not have a unit root, and hence the power of the ADF test is reduced. Therefore, relevant deterministic terms should be included.

The recommended method of choosing appropriate deterministic terms is by including the deterministic terms that are significant at 10% level. In case the deterministic trend term is not significant at 10%, it is then dropped and the constant deterministic term is used instead. If the trend is also insignificant, then it can be dropped and the test is rerun without the deterministic term. It is important to note that the majority of macroeconomic time series require the use of the constant.

In the case that the null of the ADF test cannot be rejected, the series should be differenced and the test is rerun to make sure that the time series is stationary. If this is repeated (double differenced) and the time series is still non-stationary, then other transformations to the data such as taking the natural log(if the time series is always positive) might be required.

Example: Conducting the ADF Test

A financial analyst wishes to conduct an ADF test on the log of 20-year real GDP from 1999 to 2019. The result of the tests is shown below:

$$ \begin{array}{c|c|c|c|c|c|c} \textbf{Deterministic} & \bf{\gamma} & \bf{\delta_0} & \bf{\delta_1} & \textbf{Lags} & \bf{5\% \text{CV}} & \bf{1\% \text{CV}} \\ \hline \text{None} & {-0.004} & {} & {} & {8} & {-1.940} & {-2.570} \\ \text{} & {(-1.665)} & {} & {} & {} & {} & {} \\ \hline \text{Constant} & {-0.008} & {0.010} & {} & {4} & {-2.860} & {-3.445} \\ \text{} & {(-1.422)} & {(1.025)} & {} & {} & {} & {} \\ \hline \text{Trend} & {-0.084} & {0.188} & {} & {3} & {-3.420} & {-3.984} \\ \text{} & {(-4.376)} & {(-4.110)} & {} & {} & {} & {} \\ \end{array} $$

The output of the ADF reports the results at the different number deterministic terms (first column), and the last three columns indicate the number of lags according to AIC and the 5% and 1% critical values that are appropriate to the underlying sample size and the deterministic terms. The quantities in the parenthesis (below the parameters) are the test statistics.

Determine whether the time series contains a unit root.

Solution

The hypothesis statement of the ADF test is:

\(\text H_0:\gamma=0\) (The time series is a random walk)

\(\text H_1:\gamma < 0\) (the time series is a covariance stationary )

We begin with choosing the appropriate model. At 10%, the trend model has an absolute value of the statistic greater than the CV at 1% and 5% significance level; thus, we choose a model with the trend deterministic term.

Therefore, for this model, the null hypothesis is rejected at a 99% confidence level since |-4.376|>|-3.984|. Note that the null hypothesis is also rejected at a 95% confidence level.

Moreover, if the model was constant or no-deterministic, the null hypothesis will fail to be rejected. This reiterates the importance of choosing an appropriate model.

The Seasonal Differencing

Seasonal differencing is an alternative method of modeling the seasonal time series with a unit root. Seasonal differencing is done by subtracting the value in the same period in the previous year to remove the deterministic seasonalities, the unit root, and the time trends.

Consider the following quarterly time series with deterministic seasonalities and non-zero growth rate:

$$ \text Y_{\text t}=\beta_0+\beta_1 \text t+\gamma_1 \text D_{1 \text t}+\gamma_2 \text D_{2{\text t}}+\gamma_{3} \text D_{3\text t}+\epsilon_{\text t} $$

Where \(\epsilon_{\text t}\sim \text{WN}(0,\sigma^2)\).

Denote a seasonal \(\Delta_4 \text Y_{\text t}=\text Y_{\text t}-\text Y_{\text t-4} \)

$$ \begin{align*} \Rightarrow \Delta_4 \text Y_{\text t}=&(\beta_0+\beta_1 \text t+\gamma_1 \text D_{1 \text t}+\gamma_2 \text D_{2 \text t}+\gamma_3 \text D_{3 \text t}+\epsilon_{\text t} ) \\ &- (\beta_0+\beta_1 (\text t-4)+\gamma_1 \text D_{1\text t-4}+\gamma_2 \text D_{2\text t-4}+\gamma_3 D_{3\text t-4}+\epsilon_{\text t-4} ) \\ =&\beta_1 (\text t-(\text t-4))-[\gamma_1 (\text D_{1\text t}-\text D_{1\text t-4} )+\gamma_1 (\text D_{12}-\text D_{2\text t-4} )+\gamma_1 (\text D_{3\text t}-\text D_{3\text t-4} )]+\epsilon_{\text t} \\ & -\epsilon_{\text t-4} \\ \end{align*} $$

But

$$ \gamma_{\text j} (\text D_{1\text j}-\text D_{1\text j-4} )=0 $$

Because \(\text D_{1\text j}=\text D_{1\text j-4} \) by the definition of the seasonal differencing. So that:

$$ \Rightarrow Δ_4 \text Y_{\text t} =\beta_1 (\text t-(\text t-4))+\epsilon_{\text t}-\epsilon_{\text t-4 } $$

Therefore,

$$\Delta_4 \text Y_{\text t}=4\beta_1+\epsilon_{\text t}-\epsilon_{\text t-4} $$

Intuitively, this an MA(1) model, which is covariance stationary. The seasonal differenced time series is described as the year to year change in \(\text Y_{\text t}\) or year to year growth in case of logged time series.

Spurious Regression

Spurious regression is a type of regression that gives misleading statistical evidence of a linear relationship between independent non-stationary variables. This is a problem in time series analysis, but this can be avoided by making sure each of the time series in question is stationary by using methods such as first differencing and log transformation (in case the time series is positive)

Condition for Differencing in Time Series

Practically, many financial and economic time series are plausibly persistent but stationary. Therefore, differencing is only required when there is clear evidence of unit root in the time series. Moreover, when it is difficult to distinguish whether time series is stationary or not, it is a good statistical practice to generate models at both levels and the differences.

For example, we wish to model the interest rate on government bonds using an AR(3) model. The AR(3) is estimated on the levels and the differences (if we assume the existence of unit root) are modeled by AR(2) since the AR is reduced by one due to differencing. By considering the models at all levels allows us to choose the best model when the time series are highly persistent.

Forecasting

Forecasting in non-stationary time series is analogous to that of stationary time series. That is, the forecasted value at time T is the expected value of \(\text Y_{\text T+\text h}\).

Consider a linear time trend:

$$ \text Y_{\text T}=\beta_0+\beta_1 \text T+\epsilon_{\text t} $$

Intuitively,

$$ \text Y_{\text T+\text h}=\beta_0+\beta_1 (\text T+\text h)+\epsilon_{\text t+\text h} $$

Taking the expectation, we get:

$$ \begin{align*} \text E_{\text T} (\text Y_{\text T+\text h})&=\text E_{\text T} (\beta_0)+\text E_{\text T} (\beta_1 (\text T+\text h)+\text E_{\text T} (\epsilon_{\text t+\text h}) \\ \Rightarrow \text E_{\text T} (\text Y_{\text T+\text h})&=\beta_0+\beta_1 {(\text T+\text h)} \\ \end{align*} $$

This is true because of both \(\beta_0\) and \(\beta_1 (\text T+\text h)\) are constants while \(\epsilon_{\text t+\text h}\sim \text{WN}(0,\sigma^2)\).

Forecasting in Seasonal Time Series

Recall that the seasonal time series can be modeled using the dummy variables. Consequently, we need to track the period of the forecast we desire. The annual time series is given by:

$$ \text Y_{\text T}=\beta_0+\sum_{\text j=1}^{\text s-1} \gamma_{\text j} \text D_{\text {jt}} +\epsilon_{\text t} $$

The first-step forecast is:

$$ \text E_{\text T} (\text Y_{\text T+1} )=\beta_0+\gamma_{\text j} $$

Where:

\(\text j=(\text T+1)\text{mod s}\) is the forecasted period and that the forecast and the coefficient on the omitted periods is 0.

For instance, for quarterly seasonal time series that excludes the dummy variable for the fourth quarter \((\text Q_4)\), then the forecast for period 116 is given by:

$$ \begin{align*} \text E_{\text T} (\text Y_{\text T+1} ) &=\beta_0+\gamma_{\text j} \\ \text E_{\text T} (\text Y_{\text T+1} )&=\beta_0+\gamma_{(116+1)(\text{mod } 4)}=\beta_0+\gamma_1 \\ \end{align*} $$

Therefore, the h-step ahead forecast are by tracking the period of T+h so that:

$$ \text E_{\text T} (\text Y_{\text T+\text h} )=\beta_0+\gamma_{\text j} $$

Where:

$$ \text j=(\text T+\text h)\text{mod s} $$

Forecasting in Log Models

Under the log model, you should note that:

$$ \text E(\text Y_{\text T+\text h} )\neq \text E(\text {ln }\text Y_{\text T+\text h} ) $$

If the residuals are Gaussian white noise, that is:

$$ \epsilon \overset { iid }{ \sim } N\left( 0,{ \sigma }^{ 2 } \right) $$

Then the properties of the log-normal can be used for forecasting. If

\(\text X\sim \text N(0,\sigma^2)\), then define \(\text W=\text e^{\text X}\sim \text{Log}⁡(\mu,\sigma^2)\). Also recall that the mean of a log-normal distribution is given by:

$$ \text E(\text W)=\text e^{\mu+\frac {\sigma^2}{2}} $$

Using this analogy, for a log-linear time trend model:

$$ \text{ln⁡ }\text Y_{\text T+\text h}=\beta_0+\beta_1 (\text Y_{\text T+\text h})+\epsilon_{\text T+\text h} $$

The forecast at time T+h,

$$ \text E_{\text T} (\text {ln }⁡ \text Y_{\text T+\text h})=\beta_0+\beta_1 (\text Y_{\text T+\text h}) $$

The variance of the shock is \(\sigma^2\) so that:

$$ \text {ln }⁡ \text Y_{\text T+\text h} \sim (\beta_0+\beta_1 (\text Y_{\text T+\text h} ),\sigma^2) $$

Thus,

$$ \text E_{\text T} (\text Y_{\text T+\text h} )=\text e^{\beta_0+\beta_1 (\text Y_{\text T+\text h} )+\frac {\sigma^2}{2}} $$

Forecasting Confidence Intervals

Confidence intervals are constructed to reflect the uncertainty of the forecasted value. The confidence interval is dependent on the variance of the forecasted error, which is defined as:

$$ \epsilon_{\text T+\text h}=\text Y_{\text T+\text h}-\text E_{\text T} (\text Y_{\text T+\text h} ) $$

i.e., it is the difference between the actual value and the forecasted value.

Consider the linear time trend model:

$$ \text Y_{\text T+\text h}=\beta_0+\beta_1 ({\text T+\text h})+\epsilon_{\text T+\text h} $$

Clearly,

$$ \text E_{\text T} (\text Y_{\text T+\text h} )=\beta_0+\beta_1 (\text T+\text h) $$

And the forecast error is \(\epsilon_{\text T+\text h}\)

If we wish to construct a 95% confidence interval, given that the forecast error is Gaussian white noise, then the confidence interval is given by:

$$ \text E_{\text T} (\text Y_{\text T+\text h} ) \pm 1.96\sigma $$

\(\sigma\) is not known and thus can be estimated by the variance of the forecast error.

Intuitively, the confidence intervals for any model can be computed depending on the individual forecast error \(\epsilon_{\text T+\text h}=\text Y_{\text T+\text h}-\text E_{\text T} (\text Y_{\text T+\text h} )\).

Example: Forecasting and Forecasting Confidence Intervals

A linear time trend model is estimated on annual government bond interest rates from the year 2000 to 2020. The model’s equation is given by:

$$ \text R_{\text t}=0.25+0.000154 \text t+\hat \epsilon_{\text t} $$

The standard deviation of the forecasting error is estimated to be σ ̂=0.0245. What is the 95% confidence interval for the second year if the forecasting residual errors (residuals) is a Gaussian white noise?

(Note that for the first time period t=2000 and the last time period is t=2020)

Solution

The second year starting from 2000 is 2002. So,

$$ \text E_{\text T} (\text R_{2002} )=0.25+0.000154×2002=0.2808308$$

The 95% confidence interval is given by:

$$ \begin{align*} \text E_{\text T} (\text Y_{\text T+\text h} ) & \pm 1.96\sigma \\ & =0.28083 \pm 1.96×0.0245 \\ & =[0.2328108, 0.3288508] \\ \end{align*} $$

So the 95% confidence interval for the interest rate is between 1.029% and 10.68%.

Question 1

The seasonal dummy model is generated on the quarterly growth rates of mortgages. The model is given by:

$$ \text Y_{\text t}=\beta_0+\sum_{\text j=1}^{\text s-1} \gamma_{\text j} \text D_{\text {jt}} +\epsilon_{\text t} $$

The estimated parameters are \(\hat \gamma_1=6.25,\hat \gamma_2=50.52,\hat \gamma_3=10.25\) and \(\hat \beta_0=-10.42\) using the data up to the end of 2019. What is the forecasted value of the growth rate of the mortgages in the second quarter of 2020?

A. 40.10

B. 34.56

C. 43.56

D. 36.90

The correct answer is A.

We need to define the set of dummy variables:

$$ \text D_{\text {jt}} = \begin{cases} 1, & \text{ for } { \text Q }_{ 2 } \\ 0, & \text{for } { \text Q }_{ 1 },{ \text Q }_{ 3 } \text { and } { \text Q }_{ 4 }\quad \end{cases} $$

So,

$$ \text E(\hat { \text Y}_{\text Q_2})=\beta_0+\sum_{\text j=1}^3 \gamma_{\text j} \text D_{\text {jt}}=-10.42+0×6.25+1×50.52+0×10.25=40.1 $$

Question 2

A mortgage analyst produced a model to predict housing starts (given in thousands) within California in the US. The time series model contains both a trend and a seasonal component and is given by the following:

$$ \text Y_{\text t}=0.2\text t+15.5+4.0×\text D_{2\text t}+6.4×\text D_{3\text t}+0.5×\text D_{4\text t} $$

The trend component is reflected in variable time(t), where (t) month and seasons are defined as follows:

$$ \begin{array}{c|c|c} \textbf{Season} & \textbf{Months} & \textbf{Dummy} \\ \hline \text{Winter} & \text{December, January, and February} & \text{} \\ \hline \text{Spring} & \text{March, April, and May} & {\text D_{2\text t}} \\ \hline \text{Summer} & \text{June, July, and August} & {{\text D_{3\text t}}} \\ \hline \text{Fall} & \text{September, October, and November} & {{\text D_{4\text t}}} \\ \end{array} $$

The model started in April 2019; for example, \(\text y_{(\text T+1)}\) refers to May 2019.

What does the model predict for March 2020?

A. 21,700 housing starts

B. 22,500 housing starts

C. 24,300 housing starts

D. 20,225 housing starts

The correct answer is A.

The model is given as:

$$ \text Y_{\text t}=0.2\text t+15.5+4.0×\text D_{2\text t}+6.4×\text D_{3\text t}+0.5×\text D_{4\text t} $$

Important: Since we have three dummies and an intercept, quarterly seasonality is reflected by the intercept (15.5) plus the three seasonal dummy variables (\(\text D_2\), \(\text D_3\), and \(\text D_4\)).

If \(\text Y_{\text T+1}\) = May 2019, then March 2020 = \(\text Y_{\text T} + 11\)

Finally, note that March falls under \(\text D_{2\text t}\)

$$ \text y_{\text T+11}=0.20×11+15.5+4.0×1=21.7 $$

Thus, the model predicts 21,700 housing starts in March 2020.