Deciphering the Liquidity and Credit C ...
After completing this reading, you should be able to: Describe the key factors... Read More
After completing this reading, you should be able to:
The buyer of an option has the right but not the obligation to exercise the option. The maximum loss to the buyer is equal to the premium paid for the option. Note that a trader pays premiums in order to obtain the right to buy or sell an underlying asset at a certain price in the future. On the other hand, the potential gains are theoretically infinite.
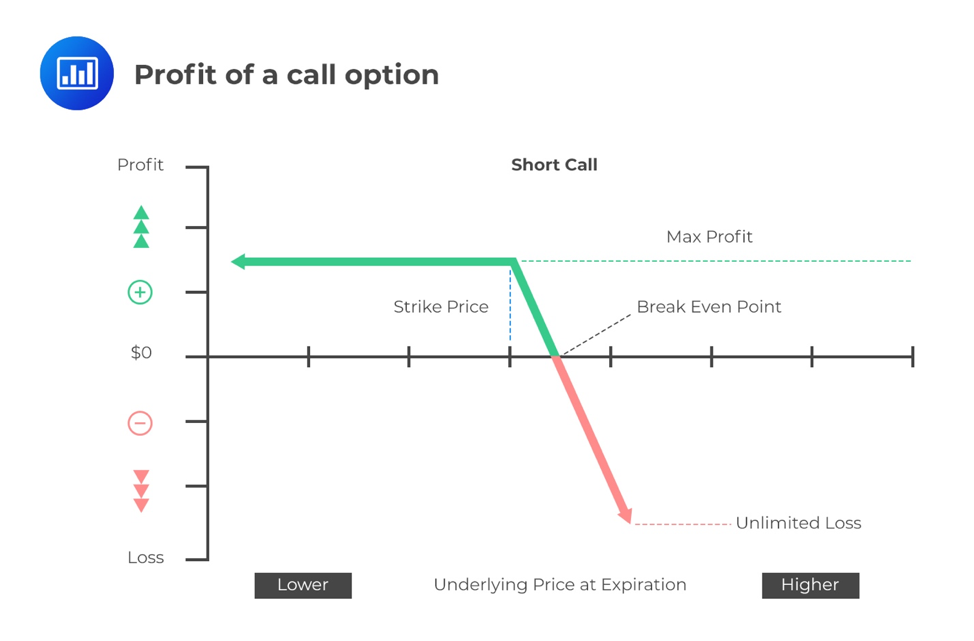
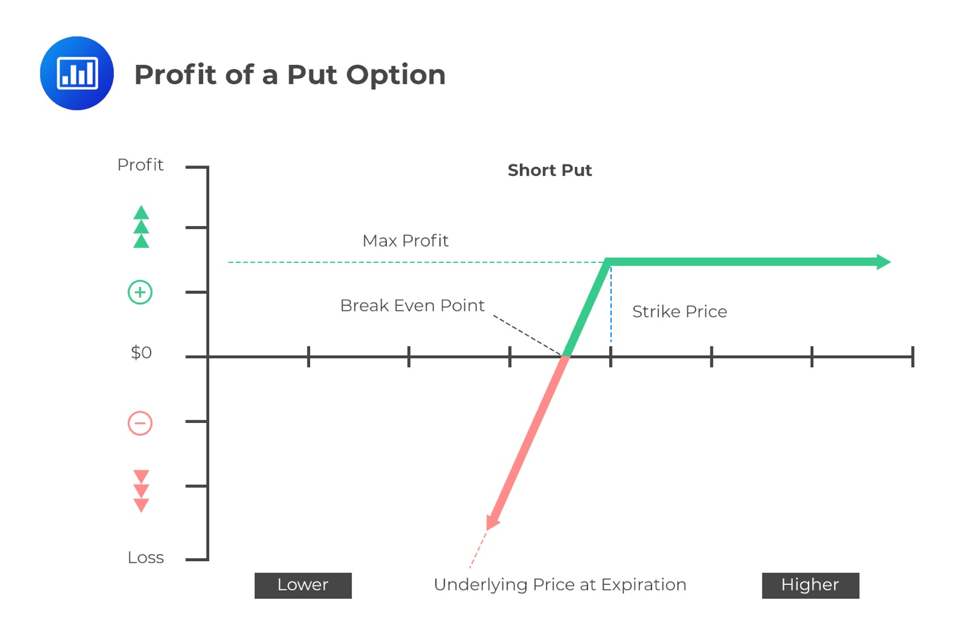
To the seller (writer), however, the maximum gain is limited to the premium received after writing the option. The potential loss is unlimited.
Some of the symbols used to represent relevant factors when dealing with options include:
\(X\) = strike price
\({ S }_{ t }\) = Price of the underlying asset at time \(t\)
\({ C }_{ t }\) = the market value of a call at time \(t\)
\({ P }_{ t }\) = the market value of put option at time \(t\)
\(t\) = the time to maturity/expiration of the option
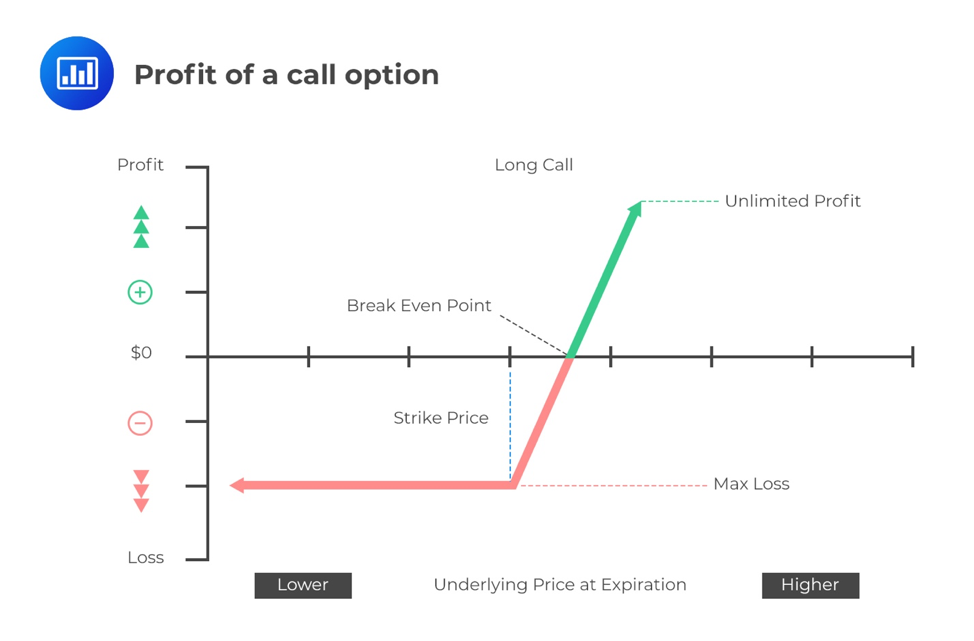
A call option gives the owner/holder/buyer the right but not the obligation to buy the underlying stock at a given price on expiry. The buyer is said to hold a long position in the contract, while the seller is said to hold a short position.
When the stock price is less than or equal to the stock price at maturity, the buyer cannot exercise the option because the payoff would be zero. If the stock price is higher than the exercise price at maturity, the buyer will most likely exercise the option. The payoff of the call will be equal to the difference between the market price and the strike price \(\left( { S }_{ t }-X \right) \).
 Put Options
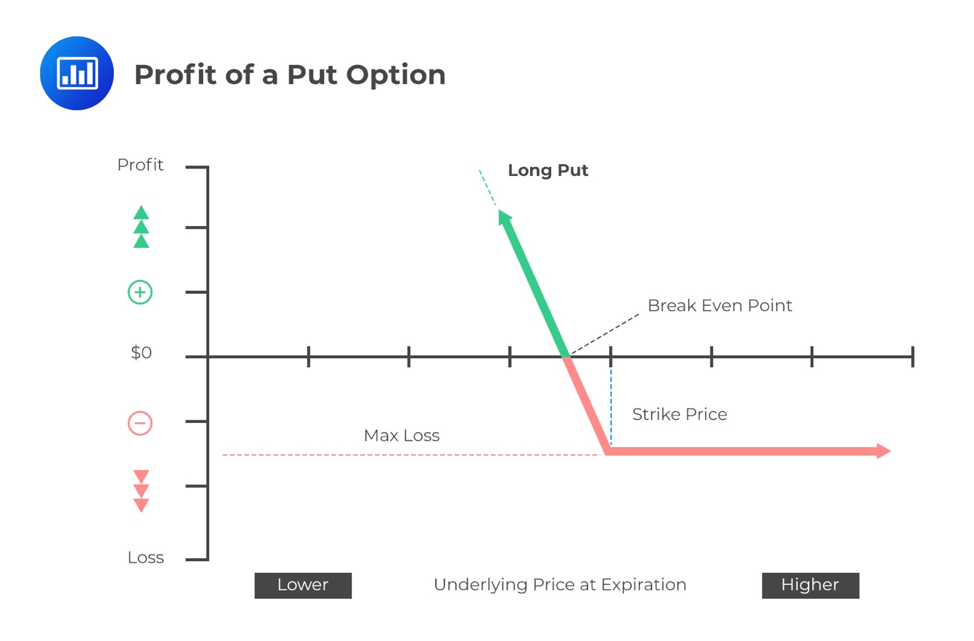
Put OptionsA put option gives the holder/buyer the right but not the obligation to sell the underlying stock at a specified price. At expiration, the buyer will only benefit if the prevailing market price is less than the exercise/strike price. The payoff is equal to \(\left( { X-S }_{ t } \right) \). If the stock stays at \(X\) or above, the payoff will be zero.
Options that can be exercised at any time, during, and before their maturity/expiration period are known as American options. Those that can only be exercised on the expiration/maturity date are known as European options. Most exchange-traded options are American options, while most options traded in over-the-counter markets are European options. Since they are only tradable at maturity, European options can easily be analyzed using the Black-Scholes-Merton model. Numerical procedures, for example, binomial trees, are used to analyze American options.
The exercise date is the date that has been specified in the contract upon which the contract matures (maturity date). The pre-determined future price at which the underlying asset will be sold is known as the exercise (or the strike) price.
Assume that options were to be exercised today. The option will be said to be:
A call (put) option is said to be in the money if the strike price is lesser (greater) than the asset price at the time of maturity of the contract. If the strike price is greater (lesser) than the asset price at the time of maturity of the contract, a call (put) option is said to be out of the money. When the asset price equals the strike price at the time of maturity, an option is said to be at the money.
A great way to visualize this concept is with a graph. Let’s say we have a call option on AAPL with a strike price of USD 150. Whenever the price of the underlying (AAPL stock) is above USD, the option is in the money:
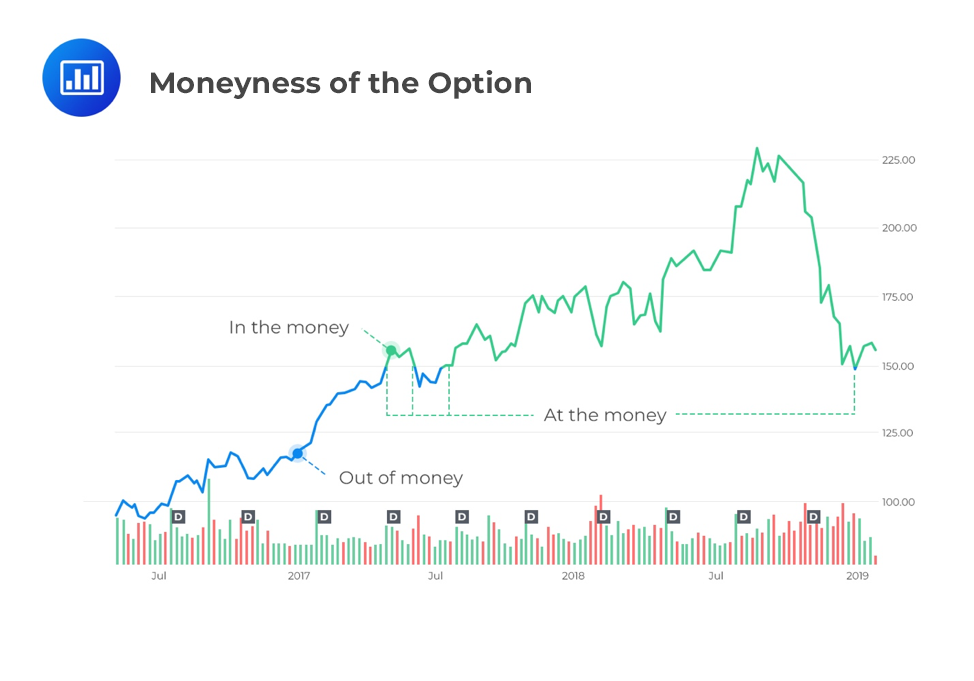
Note that for a put option with a strike price of USD 150, it would be the exact opposite – the option would be out of the money anytime the underlying stock is above USD 150.
Assume that a trader buys an out-of-the-money European call option with a strike price of \(\$50\) for an asset that is currently selling at \(\$40\). The option expires in 6 months and has a premium of \(\$5\). What are the trader’s profits/losses if the price of the underlying asset at maturity is (i) \(\$40\) and (ii) \(\$60\)?
$$ \begin{array}{l|l} \textbf{For a current asset price of \$40} & \textbf{For a current asset price of \$60} \\ \hline \begin{array}{l} \text{The option will not be} \\ \text{exercised.} \\ \text{} \\ \text{The trader therefore incurs a} \\ \text{loss of \$5, the premium paid} \\ \text{to secure the option.} \\ \text{} \\ \text{The seller of the call option} \\ \text{earns a profit of \$5.} \end{array} & \begin{array}{l} \text{The option will be exercised.} \\ \text{The trader will buy the asset at} \\ \text{\$50 and then sell it at \$60.} \\ \text{} \\ \text{The trader will, as a result,} \\ \text{make a profit of \$60 (current} \\ \text{price of the asset) – \$50 (strike} \\ \text{price) – \$5 (premium paid) = \$5.} \\ \text{} \\ \text{The seller of the option will} \\ \text{suffer a loss of \$5.} \end{array} \\ \end{array} $$
Sometimes a trader may get a net loss by exercising an option. This usually happens in cases where the current price of the underlying asset is between the strike price and the strike price plus the premium paid. In the above illustration, a trader will suffer a net loss if the asset’s current price is between $50 and $(50+5) = $55.
Suppose that the current market price of the asset in example 1 is $53. What is the trader’s net loss?
The trader will lose $5 if he chooses not to exercise the option.
If the option is exercised, the trader gets a negative profit: $53 – $50 – $5 = -$2.
In as much as the trader suffers a loss by exercising the option, the loss is smaller as compared to the loss obtained if the option is not exercised. In such a scenario, the profits made by the call option seller will also be less than $5.
Assume that a trader buys an out-of-the-money European put option with a strike price of $50 for an asset that is currently selling at $40. The option expires in 6 months and has a premium of $5. What are the trader’s profits/losses if the price of the underlying asset at maturity is (i) $40 and (ii) $60?
$$ \begin{array}{l|l} \textbf{For a current asset price of \$40} & \textbf{For a current asset price of \$60} \\ \hline \begin{array}{l} \text{If the option will be exercised:} \\ \text{The trader’s profit will be the} \\ \text{\$10 difference minus the \$5} \\ \text{premium.} \\ \text{} \\ \text{Since it’s a zero-sum game, the} \\ \text{option seller will lose \$5.} \end{array} & \begin{array}{l} \text{If the option is not} \\ \text{exercised:} \\ \text{} \\ \text{The option buyer will lose the} \\ \text{\$5 premium while the option} \\ \text{seller will gain the \$5 premium} \\ \text{paid upfront.} \end{array} \\ \end{array} $$
The trader suffers a net loss if the current market price of the asset is between the strike price minus the premium paid and the strike price, in this case, $45 and $50. For example, if the underlying price at expiration is $49, the put buyer will make $1 from the option being in the money and lose $5 from the option premium paid upfront, for a net loss of $4. This is still better than losing the full option premium of $5!
Denoting the price of the asset at maturity as \({ S }_{ t }\) and the strike price as \(X\), the payoffs from option positions are as shown below.
Long Call: \(\max( { S }_{ t }-X,0) \)
Short Call: \(-\max( { S }_{ t }-X,0) \) = \(min( X-{ S }_{ t },0) \)
Long Put: \(\max( X-{ S }_{ t },0) \)
Short Put: \(-\max( X-{ S }_{ t },0) \) = \(min( { S }_{ t }-X,0) \)
The intrinsic value is the value of the option if the option were to be exercised immediately. It is the same mathematical formula as if the payoff of the option was today.
Long Call: \(\max( { S }_{ t }-X,0) \)
Long Put: \(\max( X-{ S }_{ t },0) \)
The time value of an option is the difference between the option premium and the intrinsic value:
\(\text{Option premium}=\text{Time value}+\text{Intrinsic value}\)
Instead of paying cash, a stock dividend involves issuing extra shares to shareholders. For example, if a firm announces a 2% stock dividend, then for every 100 shares held, shareholders will receive 2 more shares.
Exchange-traded options are not usually adjusted for cash dividends. In other words, when a cash dividend occurs, there are no adjustments to the terms of the option contract.
However, when the cash dividend is larger than usual, say, more than 10%, then a committee may be formed by the Options Clearing Corporation to decide if necessary to make adjustments.
A stock split involves increasing the total number of shares outstanding by issuing more shares to shareholders at a specified ratio. For example, a 2-for-1 stock split means a shareholder will be awarded one more share for every two shares held.
If a stock has a b-for-a stock split, the share price will be reduced by a factor of (a/b). However, this is a theoretical assumption. In reality, the post-split share price can be different. The number of shares will increase by a multiple of (b/a).
The terms of exchange-traded options contracts are adjusted to reflect expected changes in a stock price arising from a stock split.
Most options exchanges use market makers to facilitate trading. The market maker will quote bids and offer prices.
A commission refers to the fee charged by a broker as a reward for their efforts in facilitating a transaction. Commission costs depend on the size of the trade as well as on the type of broker involved. They reduce the investor’s returns.
Options can be closed out by taking an offsetting position, just like future markets.
To prevent the options markets from being influenced by just the investors, the CBOE imposes position and exercise limits on traded options:
In options trading, the term “margin” refers to the collateral deposited by the option writer as a form of guarantee that they will honor their contractual obligations. Margin requirements differ from one broker to another and also depend on the nature of the underlying asset. As a general rule, options that mature before 9 months cannot be purchased on margin. Those that mature after 9 months can be purchased by borrowing up to 25% of the purchase price.
There is no margin requirement in case a trader pays cash for the option.
As discussed earlier in chapter 5;
The margin requirement by CBOE on a short call option is the maximum between the following two values:
The margin on a short put option is the maximum between the following two variables:
If the option is on indices, then the 20% in the above formulas is replaced by 15%.
Warrants are call options that are issued by a corporation.
The holder of a warrant contacts the issuer in order to exercise the warrant. When the holder of a warrant exercises his/her right to obtain shares in the company, the company issues more stock, after which the warrant holder can now buy the stock at the strike price. The issuances of debts can be made more attractive by the use of warrants.
Convertible bonds are bonds that can be converted to equity using a ratio that has been pre-determined. For example, assume the current share price of a company is USD 30. It could decide to issue 5-year bonds, each with a par value of $100 that can be converted into 10 shares after 2 years. When an investor decides to convert, the company will actually issue more shares in return for the bonds.
Both warrants and convertible bonds are usually traded on exchanges.
A corporation grants employee stock options to its employees.
Employee stock options differ from Exchange-traded option in the following ways:
Question
An investor is considering the purchase of a put option and wants to calculate its intrinsic value to determine its potential profitability. Suppose the strike price of the put option is $63 and the prevailing market price of the underlying is $78. What is the intrinsic value of the put option?
A. $15
B. -$15
C. $7.5
D. $0
The correct answer is D.
The intrinsic value of a put option is calculated as the maximum of zero or the difference between the strike price (X) and the current market price of the underlying asset (St). Mathematically, this can be expressed as:
$$ \begin{align*} \text{Intrinsic value of a put option} &= \max\left( 0,{ X-S }_{ t } \right) \\ &=\max(0,63-78) =\max(0,-15) = 0 \\ \end{align*} $$