Arbitrage Opportunities Involving Options

Call Option

A hedging portfolio can be created by going long \(\phi\) units of the underlying asset and going short the call option such that the portfolio has an initial value of:

$$\text{V}_{0}=\phi\text{S}_{0}-\text{C}_{0}$$

Where:

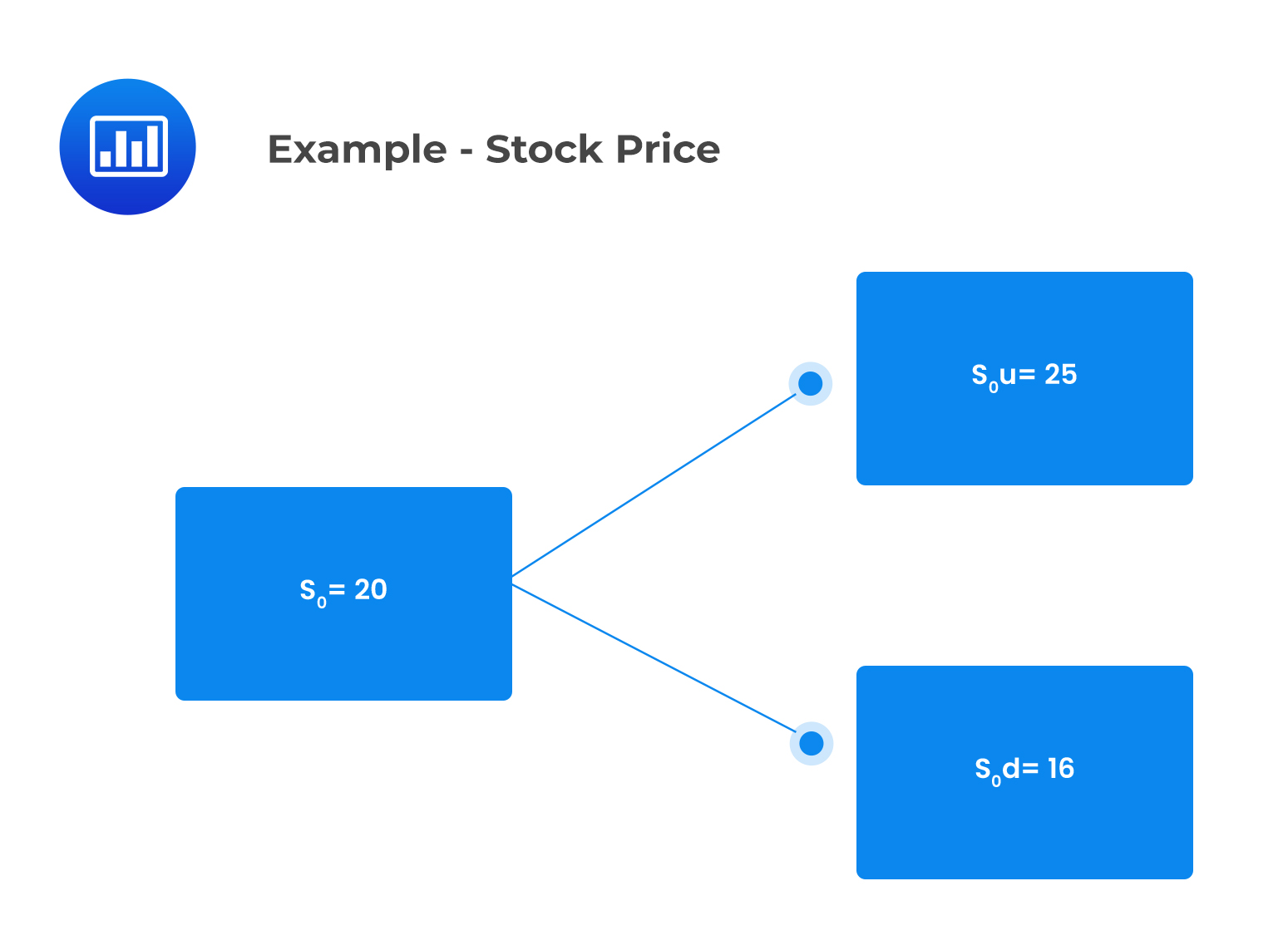
\(S_{0}\)= The current stock price

\(c_{0}=\) Current call value

After a one-time-period, this portfolio will be worth:

\(V_{1}=\phi\text{S}_{0}u-\text{c}_{u}\), if the asset price jumps up

or

\(\text{v}_{1}=\phi\text{S}_{0}\text{d}-\text{c}_{d}\) if the asset price jumps down

If we equate the values of the up and down portfolios, the number of units of the underlying asset can be obtained as:

$$\phi=\frac{c_{u}-c_{d}}{S_{0}\text{u}-S_{0}d}$$

\(\phi\) is referred to as the hedge ratio. It is the ratio that makes the trader indifferent to the movement of the underlying asset price. An arbitrageur creates a hedged portfolio to eliminate price risk, thus satisfying Rule 2: “Do not take any price risk.”

Suppose that at time step 0, a trader borrows the present value of:

$$-\phi\text{S}_{0}\text{d}+\text{c}_{\text{d}}$$

Assuming no-arbitrage, we have

$$\text{c}_{0}-\phi\text{S}_{0}=\text{PV}(-\phi\text{S}_{0}\text{d}+\text{c}_{d})$$

Since \(-\phi\text{S}_{0}\text{d}+\text{c}_{\text{d}}=-\phi\text{S}_{0}\text{u}+\text{c}_{u}\)

This can also be expressed as:

$$c_{0}-\phi\text{S}_{0}=\text{PV}(-\phi\text{S}_{0}\text{u}+\text{c}_{\text{u}})$$

The no-arbitrage single-period valuation approach leads to the following single-step call option valuation equation for call options:

$$\text{c}_{0}-\phi\text{S}_{0}=\text{PV}(-\phi\text{S}_{0}\text{d}+\text{c}_{d})$$

$$c_{0}-\phi\text{S}_{0}=\text{PV}(-\phi\text{S}_{0}\text{u}+\text{c}_{\text{u}})$$

Thus, a call option is similar to owning  units of the underlying asset and borrowing \(\text{PV}(-\phi\text{S}_{0}\text{d}+\text{c}_{\text{d}})\). This makes the transaction completely arbitrage-free, hence satisfying Rule 1: “Do not use own money.” Moreover, we can view a call option as a leveraged position in the underlying asset.

We can use the idea that a hedged portfolio returns the risk-free rate to determine the initial value of a call or a put option.

Example: Value of a Call Option

Consider a one-period binomial model of a non-dividend-paying stock whose current price is $20. Suppose that:

• Over the single period under consideration, the stock price can either jump up to $25 or down to $16
• The continuously compounded risk-free rate of return is 4% per period

The current value of a one-period European call option that has an exercise price of $20 is closest to:

Solution

The binomial tree in respect of the stock price is as follows:

Similarly, consider a corresponding binomial tree with respect to the payoff provided by the call option at time 1, I.e.,  the profit paid at exercise:

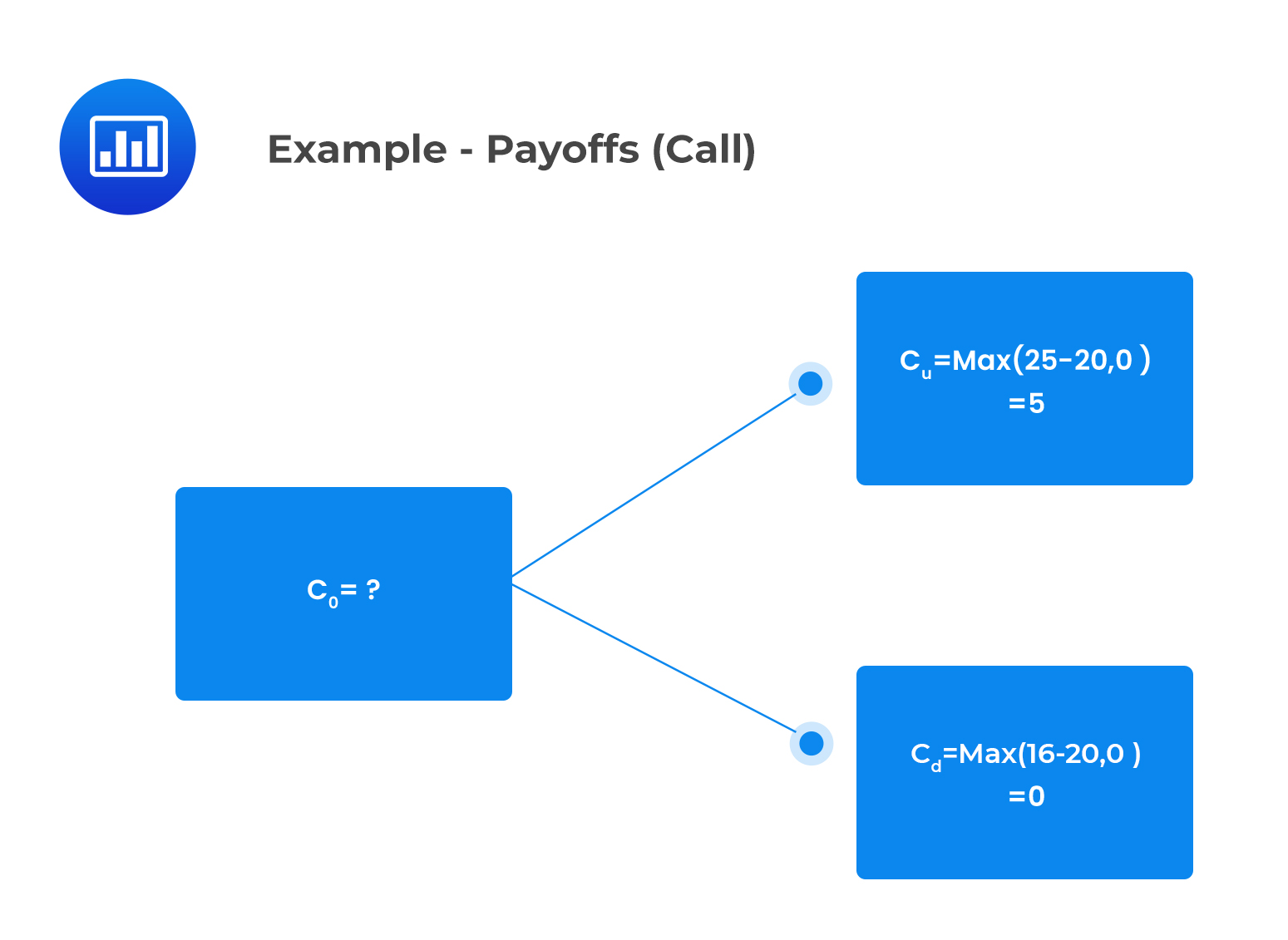We can determine \(c_{0}\) by using the single-period call option valuation equation as follows:

$$\text{c}_{0}-\phi\text{S}_{0}=\text{PV}(-\phi\text{S}_{\text{d}}+\text{c}_{d})$$

$$\begin{align*}\phi&=\frac{c_{u}-c_{d}}{S_{0}u-S_{0}d}\\&=\frac{5-0}{25-16}\\&=0.56\end{align*}$$

Thus,

$$c_{0}=0.56\times20+e^{-0.04}[-0.56\times16+0]=$2.59$$

This implies that buying a call option for $2.59 is equivalent to buying 0.56 units of the underlying stock for $11.20 and lending $8.61 such that the effective payment is $2.59

Put Options

The no-arbitrage single period valuation equation for put options is expressed as:

$$\text{p}=\phi\text{S}_{0}+\text{PV}(-\phi\text{S}_{0}\text{d}+\text{p}_{\text{d}})$$

Equivalently,

$$\text{p}=\phi\text{S}_{0}+\text{PV}(-\phi\text{S}_{0}\text{u}+\text{p}_{\text{u}})$$

Where the hedge ratio, \(\phi\) is given as:

$$\phi=\frac{p_{u}-p_{d}}{S_{0}u-S_{0}d}\leq0$$

Note that the hedge ratio, in this case, will be negative as \(p_{u}\) is less than \(p_{d}\). Thus, the arbitrageur should short-sell the underlying and lend a portion of the proceeds to replicate a long-put position.

Therefore, a put option can be viewed as equivalent to shorting the underlying asset and lending \(\text{PV}(-\phi\text{S}_{\text{u}}+\text{p}_{\text{u}})\).

Example: Value of a Put Option

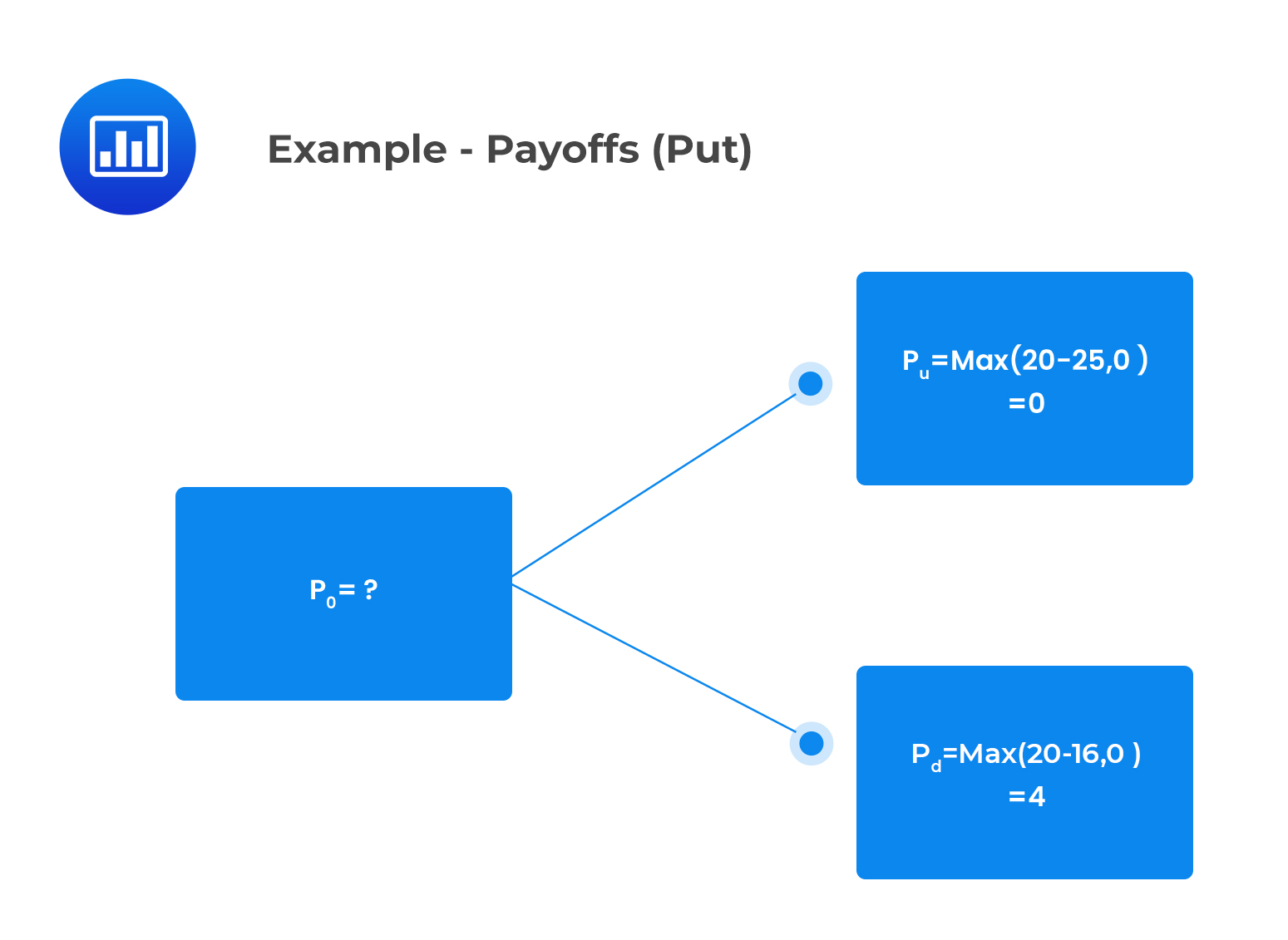
Consider a one-period binomial model of a non-dividend-paying stock whose current price is $20. Suppose that:

• Over the single period under consideration, the stock price can either jump up to $25 or down to $16
• The continuously compounded risk-free rate of return is 4% per period

The current value of a one-period European put option that has an exercise price of $20 is closest to:

Solution

The payoff provided by the put option at time one is represented in the following binomial tree:

$$p=\phi\text{S}_{0}+\text{PV}(-\phi\text{S}_{0}\text{u}+\text{p}_{u})$$

Where:

$$\begin{align*}\phi&=\frac{p_{u}-p_{d}}{S_{0}u-S_{0}d}\leq0\\&=\frac{0-4}{25-16}\\&=-0.44\end{align*}$$

$$p=-0.44\times e^{-0.04}(-{-}0.44\times25+0)=$1.77$$

Notice that buying a put option for $1.77 is equivalent to short selling 0.44 units of the underlying stock for $8.80 and lending $10.57.

Exploiting Arbitrage Opportunities

Consider a one-period binomial model of a non-dividend-paying stock whose current price is $20. Suppose that:

• Over the single period under consideration, the stock price can either jump up to $25 or down to $16
• The continuously compounded risk-free rate of return is 4% per period

In the previous section, we determined the current value of this call option as $2.59 given a strike price of $20.

Now, assume that the call option has a market price of $4.50. Assuming that we trade 1,000 call options, we can illustrate how this opportunity can be exploited to earn an arbitrage profit.

Since the call option is overpriced, we will sell 1,000 call options and buy several shares of the underlying determined by the hedge ratio.

$$\begin{align*}\phi&=\frac{c_{u}-c_{d}}{S_{0}u-S_{0}d}\\&=\frac{$5-$0}{$25-$16}\\&=\frac{5}{9} \text{shares per option}\end{align*}$$

Thus, we will purchase \(1,000\times\frac{5}{9}=\text{555.5555 shares}\)

The net cost of a portfolio with 555.55 shares of the stock held long at $20 per share and 1,000 calls held short at $4.50 is:

$$\text{Net cost of the portfolio}=(555.55\times$20)-(1,000\times$4.50)\approx$6,611$$

Assume that we begin with $0

Then borrow $6,611 at 4%

At the end of the one-time period, we repay the loan of \($6,611\times1.04\approx$6,875\)

The portfolio value will be the same at maturity regardless of whether the stock price moves up to $25 or down to $16.

Value of the portfolio after stock price moves up:

$$V_{u}=(555.55\times$25)-(1,000\times$5)\approx$8,889$$

Value of the portfolio after stock price moves down:

$$V_{d}=(555.55\times$16)-(1,000\times$0)\approx$8,889$$

Arbitrage profit on this portfolio at the end of one year if the price moves up or down after repayment of loan \(=$8,889-$6,875=$2,014\)

The discounted value of the arbitrage profit is thus:

$$\text{PV (Arbitrage profit)}=\frac{$2,014}{1.04}=$1,936.54$$

Question

Consider a non-dividend-paying stock with a current price of $50 and an exercise price of $50. The stock price can be modeled by assuming that it will either increase by 12% or decrease by 10% each year, independent of the price movement in other years. A trader constructs a portfolio consisting of 100 call options. If the call option is overpriced, the portfolio that leads to an arbitrage profit is most likely:

1. Buy 100 call options, short 54.55 shares
2. Buy 100 call options, short 45.45 shares
3. Sell 100 call options, buy 54.55 shares

Solution

The correct answer is C: 

u=1.12

d=0.90

We can represent the above information in the following binomial tree

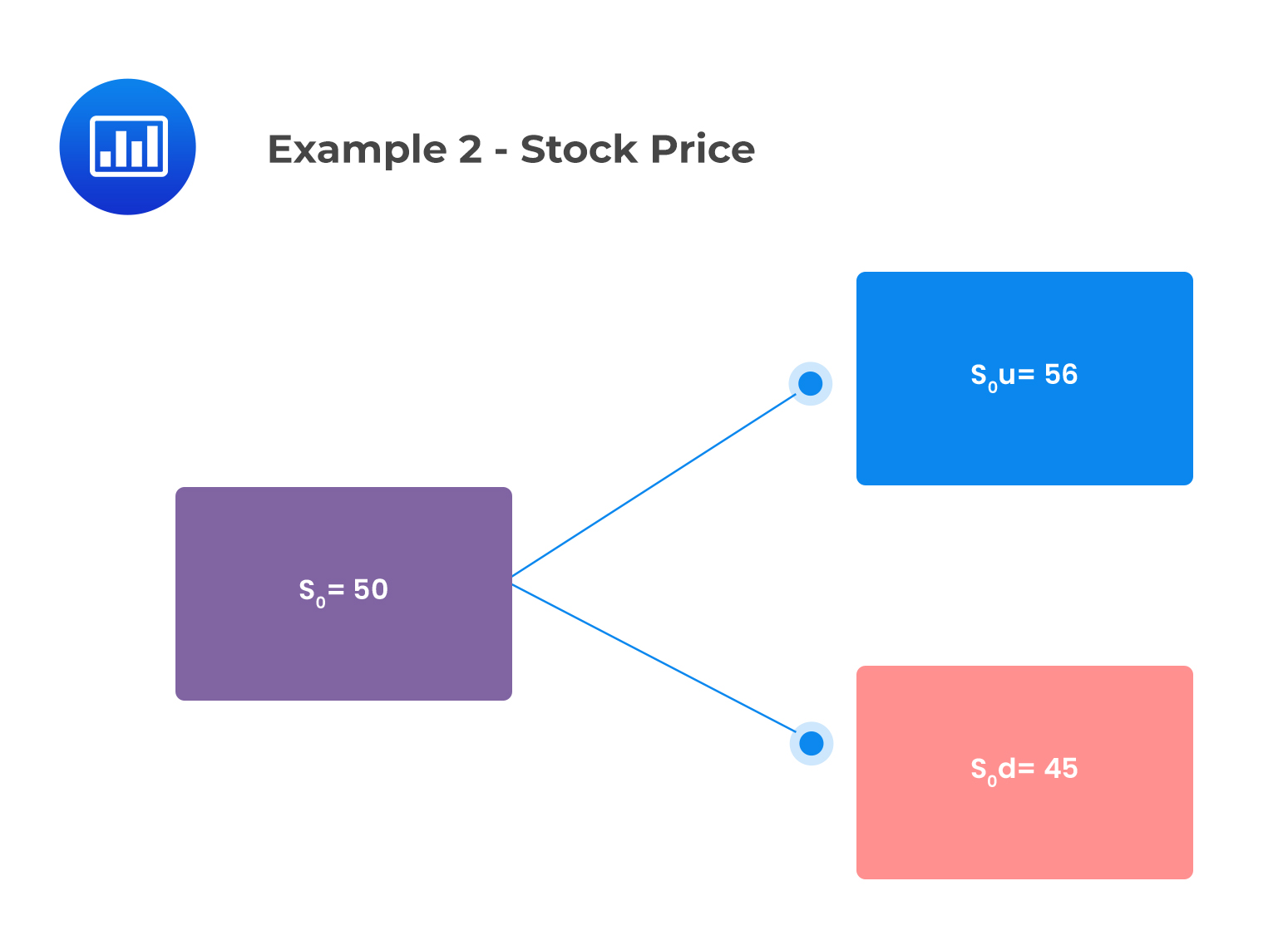The call payoffs are as follows:

$$c_{u}=max($56-$50,0)=$6$$

$$c_{d}=max($45-50,0)=$0$$

Since the option is overpriced, the trader will sell 100 call options and purchase several shares determined by the hedge ratio:

$$\begin{align*}\phi&=\frac{c_{u}-c_{d}}{S_{0}u-S_{0}d}\\&=\frac{$6-$0}{$56-$45}\\&=0.5455 \text{shares per option}\end{align*}$$

$$\text{Total number of shares to purchase}=100\times0.5455=54.55$$

Buying 54.55 shares of stock will produce a riskless hedge. The payoff at expiry will return more than the risk-free rate on the hedge portfolio’s net cost. Borrowing to finance the hedge portfolio and earning a higher rate than the borrowing rate produces riskless profits.

Reading 38: Valuation of Contingent Claims

LOS 38 (C) identify an arbitrage opportunity involving options and describe the related arbitrage