No-Arbitrage Values of Options

Valuing European Options

A European option is an option that can only be exercised at expiry.

Consider a stock with an initial price of $70 and a risk-free rate of 1% per year. The asset price can move up by 10% or down by 10%. The price of a European call and put options with two years to maturity and a strike price of $80 using a two-period binomial model is closest to:

Call option

Recall the two-period binomial formula for pricing a call option from the previous section:

$$c_{0}=\frac{q^{2}c_{uu}+2q(1-q)c_{ud}+(1-q)^{2}c_{dd}}{(1+r)^{2}}$$

Where: 

\(u=\) Up-move factor = 1.10

\(d=\) Down-move factor = 0.90

and the risk-neutral probability, q, is given by: 

$$q=\frac{(1+r)-d}{u-d}$$

The stock prices at each node and the call option payoffs are shown in the following binomial tree.

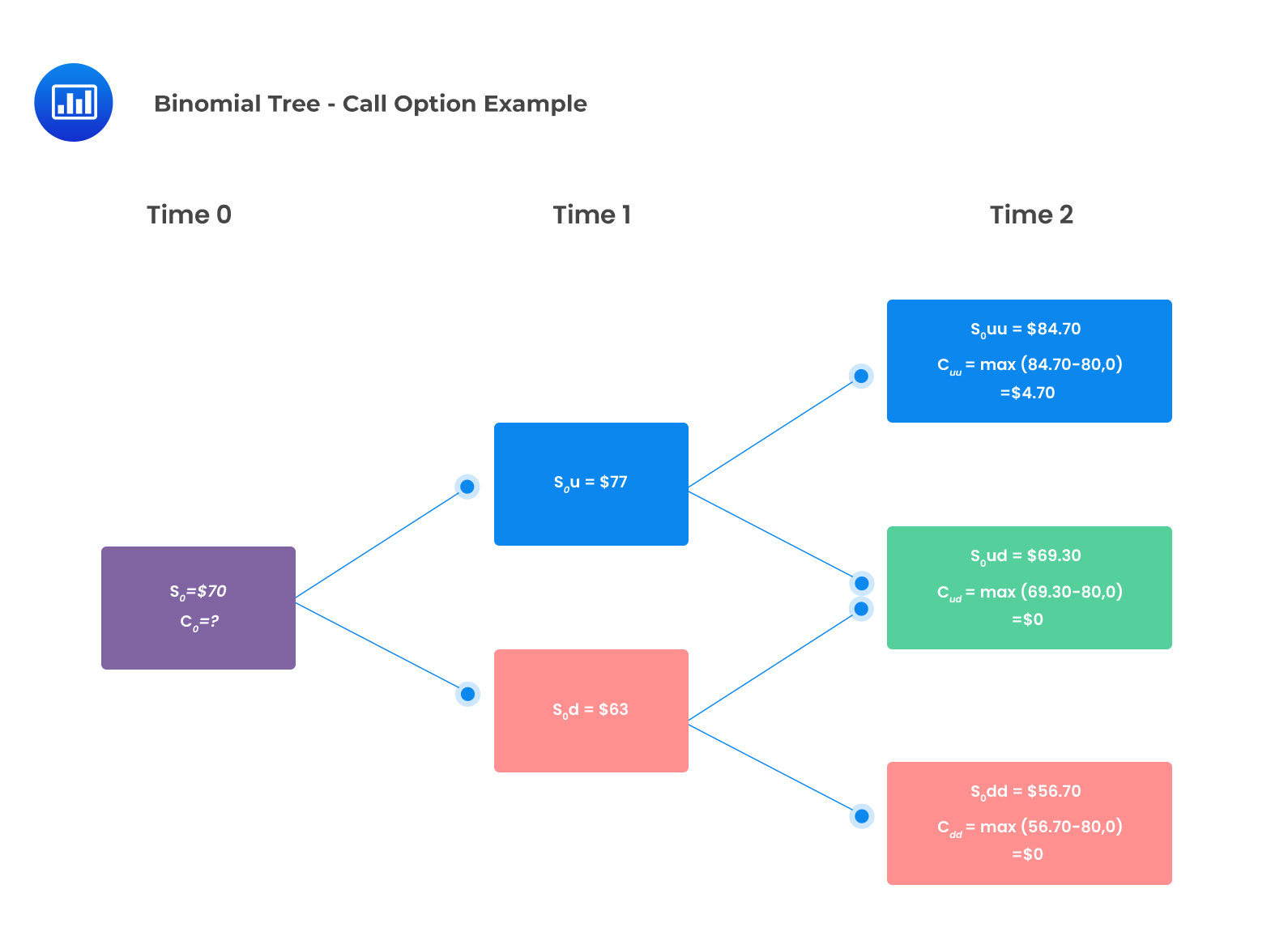The risk-neural probability, q, is given by:

$$\begin{align*}q&=\frac{(1+r)-d}{u-d}\\&=\frac{(1.01)-0.9}{(1.1-0.9)}\\&=0.55\end{align*}$$

The two-period binomial value of the call option:

$$\begin{align*}c_{0}&=\frac{q^{2}c_{uu}+2q(1-q)c_{ud}+(1-q)^{2}c_{dd}}{(1+r)^{2}}\\&=\frac{0.55^{2}\times$4.70+2\times0.55(1-0.55)\times0+(1-0.55)^2\times0}{(1.01)^2}\\&=$1.39\end{align*}$$

Put option

The stock prices and the put option payoffs are shown in the following two-period binomial tree:

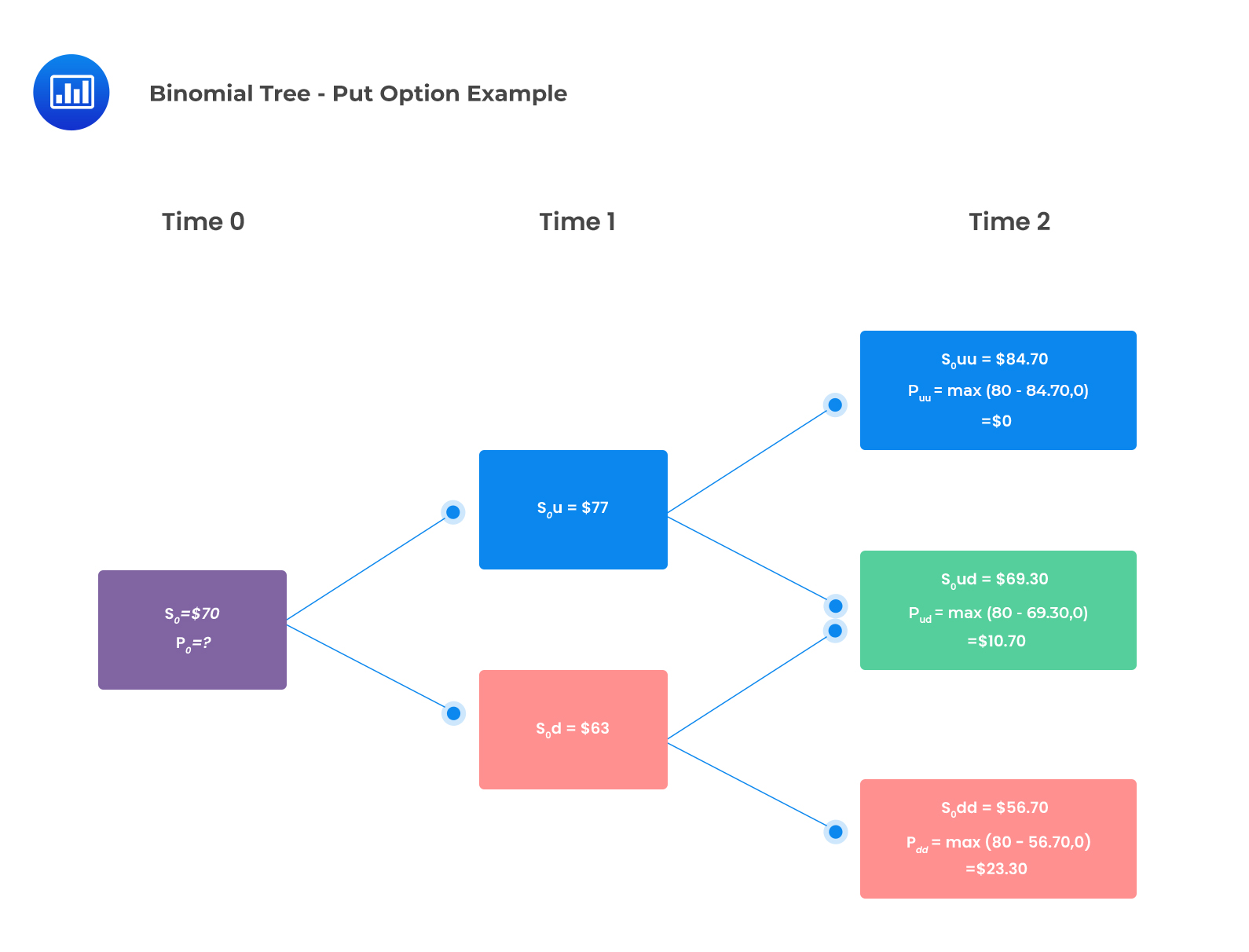We determined q to be 0.55;

Using the formula:

$$\begin{align*}p_{0}&=\frac{q^{2}p_{uu}+2q(1-q)p_{ud}+(1-q)^{2}p_{dd}}{(1+r)^{2}}\\&=\frac{0.55^{2}\times0+2\times0.55\times0.45\times$10.70+0.45^{2}\times$23.30}{1.01^{2}}\\&=$9.82\end{align*}$$

Valuing American Options

The difference between an American and a European option is that with an American option, the holder can exercise the option before the expiry date, not just on the expiry date as with a  European option. Thus, the value of an American option may be higher than that of a comparable European option due to the early exercise feature.

The difference between the value of an American option and a comparable European option is referred to as the early exercise premium.

$$\text{Early exercise premium} = \text{American option value} – \text{European option value}$$

American calls on non-dividend paying stocks do not benefit from the early exercise feature. However, American puts may have an early exercise premium and must be checked for early exercise. An early exercise captures the options’ intrinsic value and forgoes the time value.

It is worth noting that deep in the money, American put options cannot be valued simply as the discounted value of the expected future option payouts. Therefore, we must establish whether or not early exercise is optimal at each node by working backward through the binomial tree.

The unexercised American option values at time one is determined using the following formulas:

$$p_{u}=\frac{qp_{uu}+(1-q)p_{ud}}{(1+r)}$$

$$p_{u}=\frac{qp_{ud}+(1-q)p_{dd}}{(1+r)}$$

The next step is to check each node for early exercise.

Example: Calculating the Value of an American Put Option

Consider a non-dividend-paying stock with an initial price of $70 and a risk-free rate of 1% compounded annually. The asset price can move up by 10% or down by 10%. The price of an American put option with two years to maturity and a strike price of $80 using a two-period binomial model is closest to:

Solution

The put option’s payoffs at time two have been calculated as illustrated in the following binomial tree.

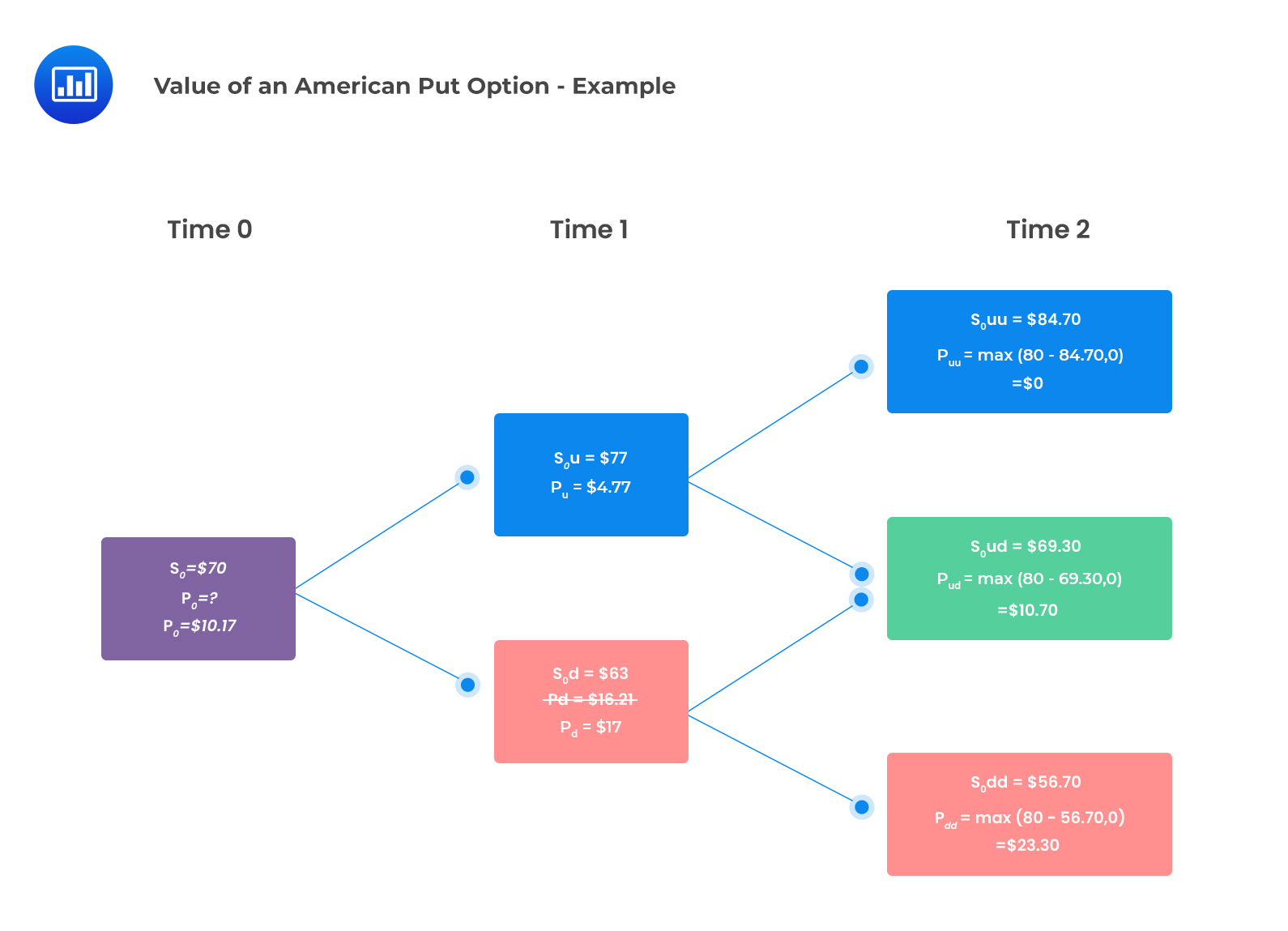At time one, the unexercised values of the option are determined as follows:

$$\begin{align*}p_{u}&=\frac{qp_{uu}+(1-q)p_{ud}}{(1+r)}\\&=\frac{0.55\times$0+(1-0.55)\times$10.70}{(1.01)}\\&=$4.77\end{align*}$$

$$\begin{align*}p_{d}&=\frac{qp_{ud}+(1-q)p_{dd}}{(1+r)}\\&=\frac{0.55\times$10.70+(1-0.55)\times$23.30}{1.01}\\&=$16.21\end{align*}$$

The next step is to evaluate whether it is optimal for early exercise at each node:

The value at the up-jump node \(= max($4.77,$80-$77)=$4.77\)

The value at the down-jump node  \(= max($16.21,$80-$63) = $17\)

The value of the American put at t=0 is then calculated as follows:

$$\begin{align*}p_{0}&=\frac{qp_{u}+(1-q)p_{d}}{1+r}\\&=\frac{(0.55\times$4.77)+(1-0.55)\times$17}{1.01}\\&=$10.17\end{align*}$$

Recall that the value of a comparable European put option was determined as $9.82.

Notice that the American put is worth more than a similar European put.

$$\text{Early exercise premium}=$10.17-$9.82=$0.35$$

Question

Consider the following information:

• \(S_{0}=$30\)
• \(K=$29\)
• \(U=1.3333\bigg(\frac{4}{3}\bigg)\)
• \(d=0.75\)
• \(n=\text{2 years}\)
• \(r=\text{2% compounded annually}\)
• No dividends

Using a two-period binomial model, the early exercise premium of an American-style put option is closest to:

1. $0.00
2. $0.06
3. $3.36

Solution

The correct answer is B:

$$\text{Early exercise premium} = \text{American put value} – \text{European put value}$$

European put value

We determine the value of the European put by constructing an appropriate binomial tree and applying the relevant formulas as follows:

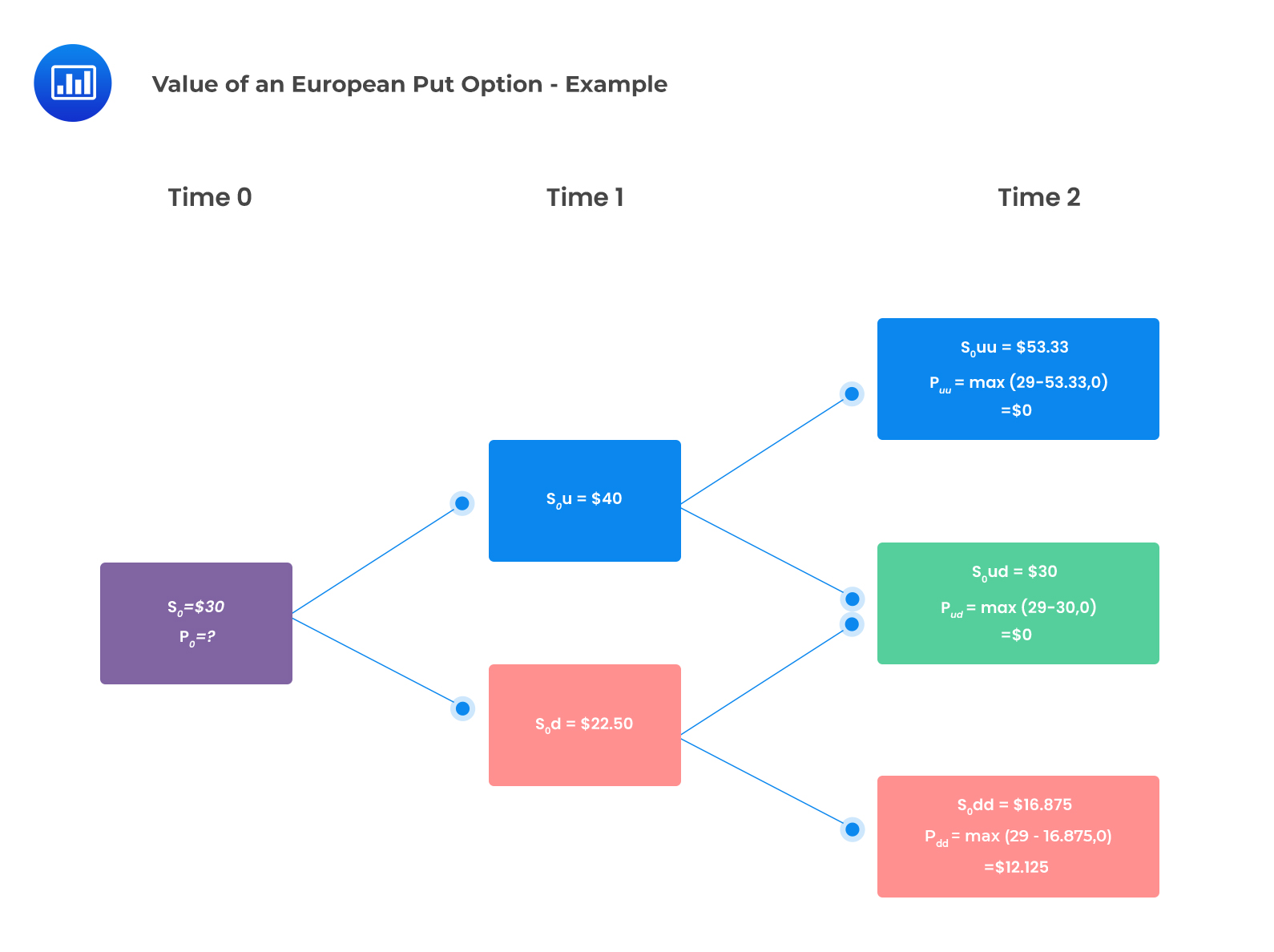Formula:

$$p_{0}=\frac{q^{2}p_{uu}+2q(1-q)p_{ud}+(1-q)^{2}p_{dd}}{(1+r)^{2}}$$

Where: 

$$\begin{align*}q&=\frac{(1+r)-d}{u-d}\\&=\frac{1.02-0.75}{1.3333-0.75}\\&=0.463\end{align*}$$

$$\begin{align*}p_{0}&=\frac{0.463^{2}\times0+2\times0.463\times0.537\times$0+0.537^{2}\times$12.125}{1.02^{2}}\\&=$3.361\end{align*}$$

American put value

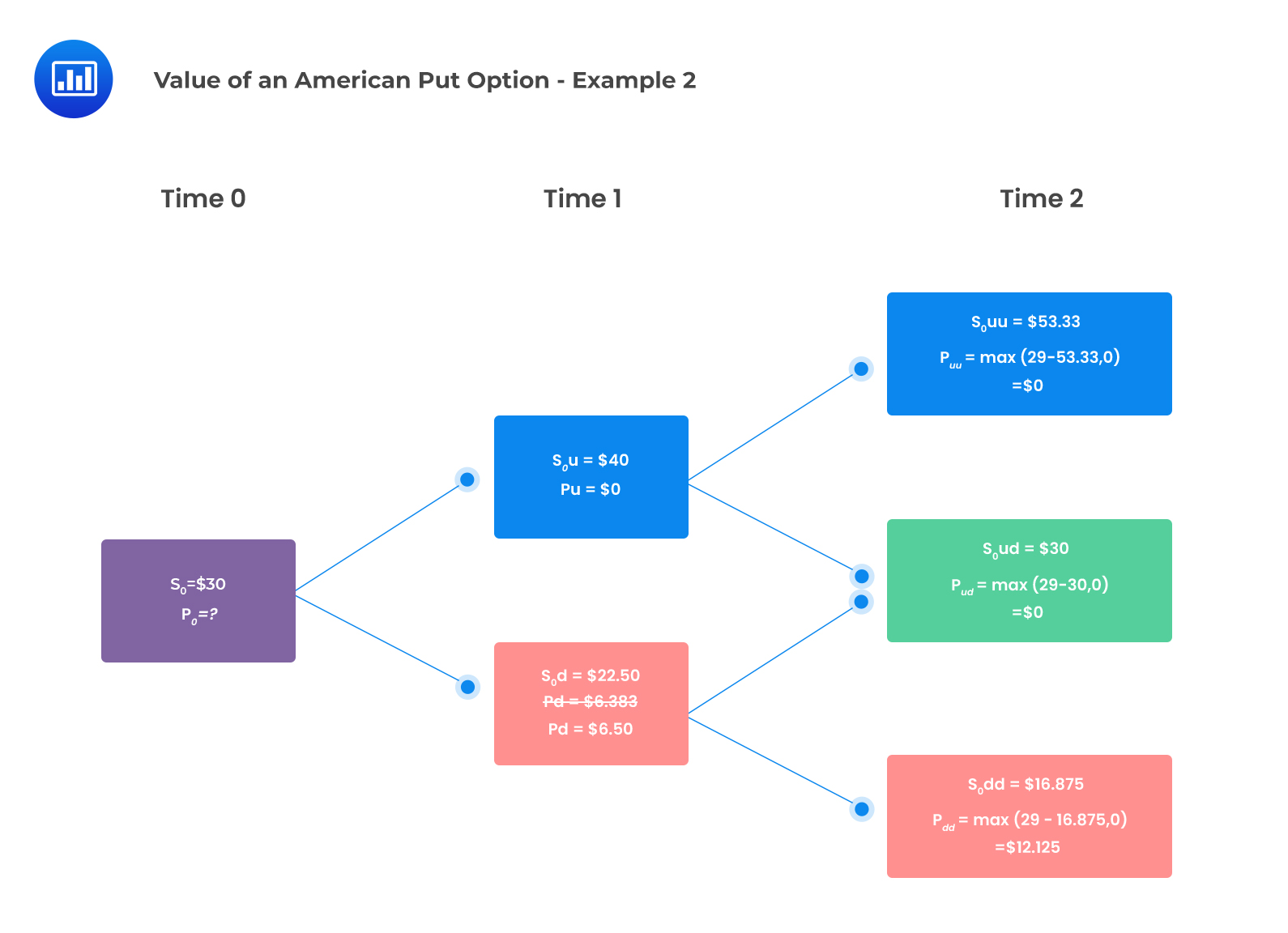At time one, the unexercised values of the option are determined as follows:

$$\begin{align*}p_{u}&=\frac{qp_{uu}+(1-q)p_{ud}}{(1+r)}\\&=\frac{0.463\times$0+0.537\times0}{(1.02)}\\&=$0\end{align*}$$

$$\begin{align*}p_{u}&=\frac{qp_{ud}+(1-q)p_{dd}}{(1+r)}\\&=\frac{0.463\times$0+0.537\times$12.125}{1.02}=$6.383\end{align*}$$

The next step is to evaluate whether it is optimal for early exercise at each node:

The value at the down-jump node  = max($6.383,$29-$22.50) = $6.50

The value of the American put at t=0 is then calculated as follows:

$$\begin{align*}p_{0}&=qp_{u}+(1-q)p_{d}\\&=\frac{(0.463\times$0)+0.537\times$6.50}{1.02}\\&=$3.422\end{align*}$$

The American put is worth more than a comparable European put as  \($3.422>$3.361\)

Thus,

$$\text{Early exercise premium}=$3.422-$3.361=$0.061$$

Reading 38: Valuation of Contingent Claims

LOS 38 (b) calculate the no-arbitrage values of European and American options using a two-period binomial model