Expectations Valuation Approach

One-step Binomial Tree

Since a hedged portfolio returns the risk-free rate, it can determine the initial value of a call or put. The expectations approach calculates the values of the option by taking the present value of the expected terminal option payoffs. This approach utilizes risk-neutral probabilities instead of true probabilities.

Therefore, the initial value of a call and put respectively are determined using the following formulas:

$$ c_0=\frac{qc_u+\left(1-q\right)c_d}{1+r} $$

And

$$ p_0=\frac{qp_u+\left(1-q\right)p_d}{1+r} $$

Where:

$$ q=\frac{\left(1+r\right)-d}{u-d} $$

Where

\(r\) is the risk-free rate for a single period.

\(q\) gives the risk-neutral probability of an upward move in price, while \((1-q)\) gives the probability of a downward move.

Example: Expectations Approach for One-step Binomial Tree

Consider a stock that is currently trading at $50. Assume that the up jump and down jump factors for the stock price are u = 1.20 and d = 0.80. The risk-free rate compounded periodically is 4%. Given a strike price of $50, we can use a single period binomial model to price European call and put options.

Price of a European Call Option

Note that:

$$ \begin{align*} c_T &=max{\left(S_T-K,0\right)} \\ S_0u & =50\times1.20=$60 \\ S_0d &=50\times0.80=$40 \\ c_u &=max\left($60-$50,0\right)=$10 \\ c_d &=max\left($40-$50,0\right)=$0 \end{align*} $$

The value of the call option can then be determined using the formula:

$$ c_0=\frac{qc_u+\left(1-q\right)c_d}{1+r} $$

Where:

$$ \begin{align*} q &=\frac{\left(1+r\right)-d}{u-d} \\ q &=\frac{\left(1.04\right)-0.8}{1.20-0.80}=0.6 \\ c_0 &=\frac{0.6\times$10+\left(1-0.6\right)\times0}{1.04}=$5.77 \end{align*} $$

Price of a European Put Option

$$ \begin{align*} p_T &=max{\left(K-S_T,0\right)} \\ p_u &=max\left($50-$60,0\right)=$0 \\ p_d &=max\left($50-$40,0\right)=$10 \\ p_0 &=\frac{qp_u+\left(1-q\right)p_d}{1+r} \\ p_0 &=\frac{0.60\times0+\left(1-0.60\right)\times$10}{1.04} \\ p_0 &=$3.85 \end{align*} $$

Two-step Binomial Tree

The expectations approach can also be applied to the two-step binomial model to determine the value of options.

Let \(q\) be the risk-neutral probability of an up move. In this instance, the price of a European call option can be determined using the two-step binomial model:

$$ c_o=\frac{q^2c_{uu} + 2q\left(1-q\right)c_{ud} +\left(1 – q\right)^2c_{dd}}{\left(1 + r\right)^2} $$

The two-period European put value is given as:

$$ p_o=\frac{q^2p_{uu} + 2q\left(1-q\right)p_{ud} +\left(1- q\right)^2p_{dd}}{\left(1 + r\right)^2} $$

Example: Expectations Approach for two-Step Binomial Model

Assume that you have a stock that is currently trading at $60. A two-year European call option on the stock is available with a strike price of $60. The risk-free rate is 2% per annum. Given that the up-move factor is 1.10 and the down-move factor is 0.90, the value of the call option using a two-period binomial model is closest to:

Solution

The risk-neutral probability of an up-move is given by:

$$ \begin{align*} q &=\frac{\left(1+r\right)-d}{u-d} \\ q &=\frac{1.02-0.90}{1.1-0.9}=0.6 \end{align*} $$

$$ \text{The probability of down move } (1-q) = 1-0.6 = 0.4 $$

The two-period binomial tree is shown below:

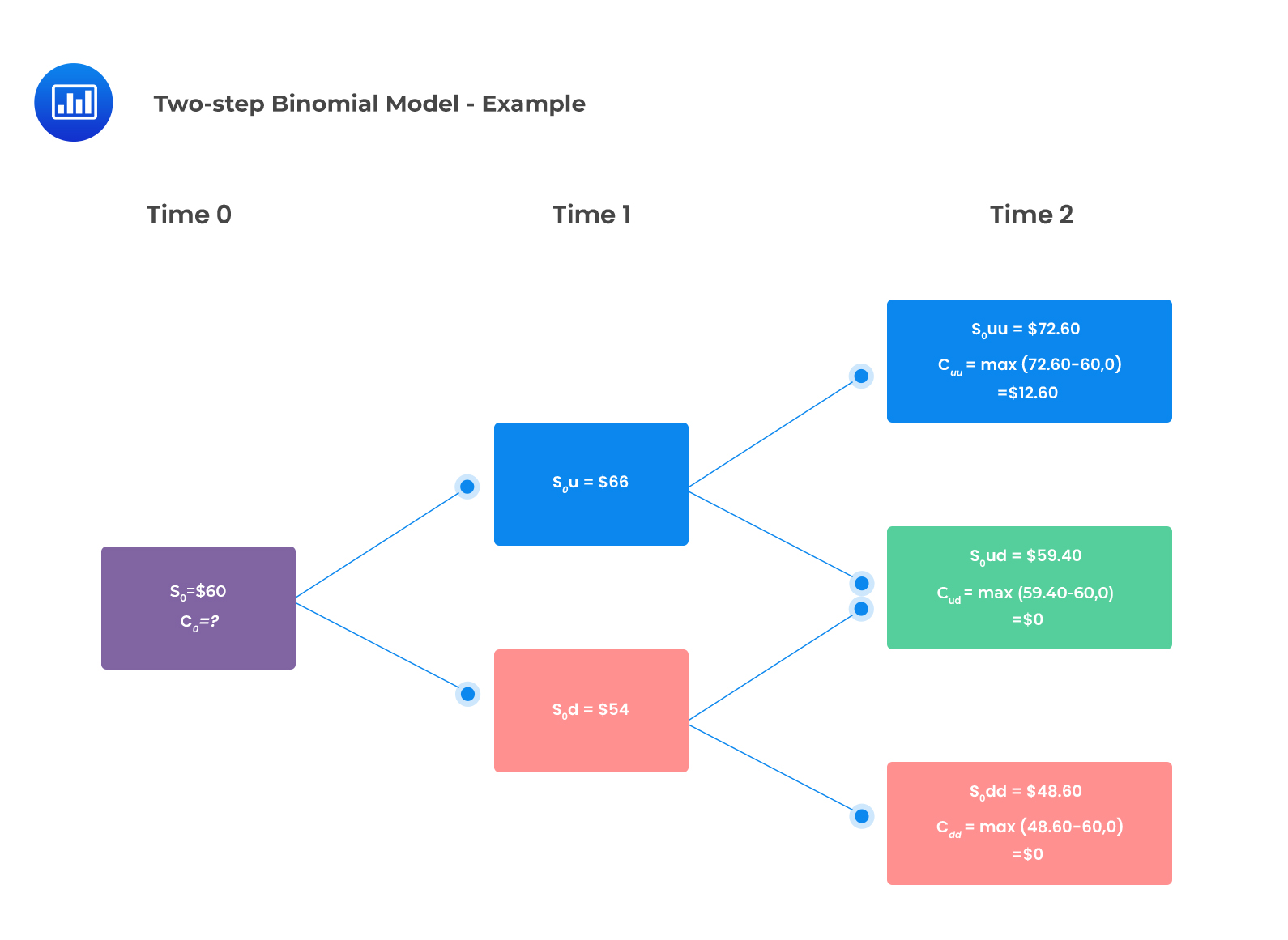The two-period binomial value of the call option:

$$ \begin{align*} c_o &=\frac{q^2c_{uu} + 2q\left(1-q\right)c_{ud} +\left(1 – q\right)^2c_{dd}}{\left(1 + r\right)^2} \\ c_0 &=\frac{{0.6}^2\times$12.60+2\times0.6\times0.4\times0+{0.4}^2\times0}{\left(1.02\right)^2} \\ c_0 & =$4.36 \end{align*} $$

Question

Nabi Gudka, CFA, applies the expectations approach to value a European call option on the common shares of Wipro Inc. The expectation approach most likely utilizes:

1. A risk premium for discounting.
2. Risk-neutral probabilities.
3. Actual probabilities.

Solution

The correct answer is A.

Under the expectations approach, the expected future payoff is calculated using risk-neutral probabilities, and the expected payoff is discounted at the risk-free rate. 

Reading 34: Valuation of Contingent Claims

LOS 34 (e) Describe how the value of a European option can be analyzed as the present value of the option’s expected payoff at expiration.