State Bayes Theorem and use it to calculate conditional probabilities

Bayes Theorem

Before we move on to Bayes Theorem, we need to learn about the law of total probability.

The Law of Total Probability

The law of total probability states that if E is an event, and \(A_1, A_2, \cdots A_n\) are the partition of the sample space, then

$$P(E)=P(A_1 \cap E)+P(A_2 \cap E)+\cdots P(A_n \cap E)$$

We can use the law intuitively by recalling that:

$$A=(A\cap B)\cup (A\cap B^c)$$

Consider the following Venn Diagram:

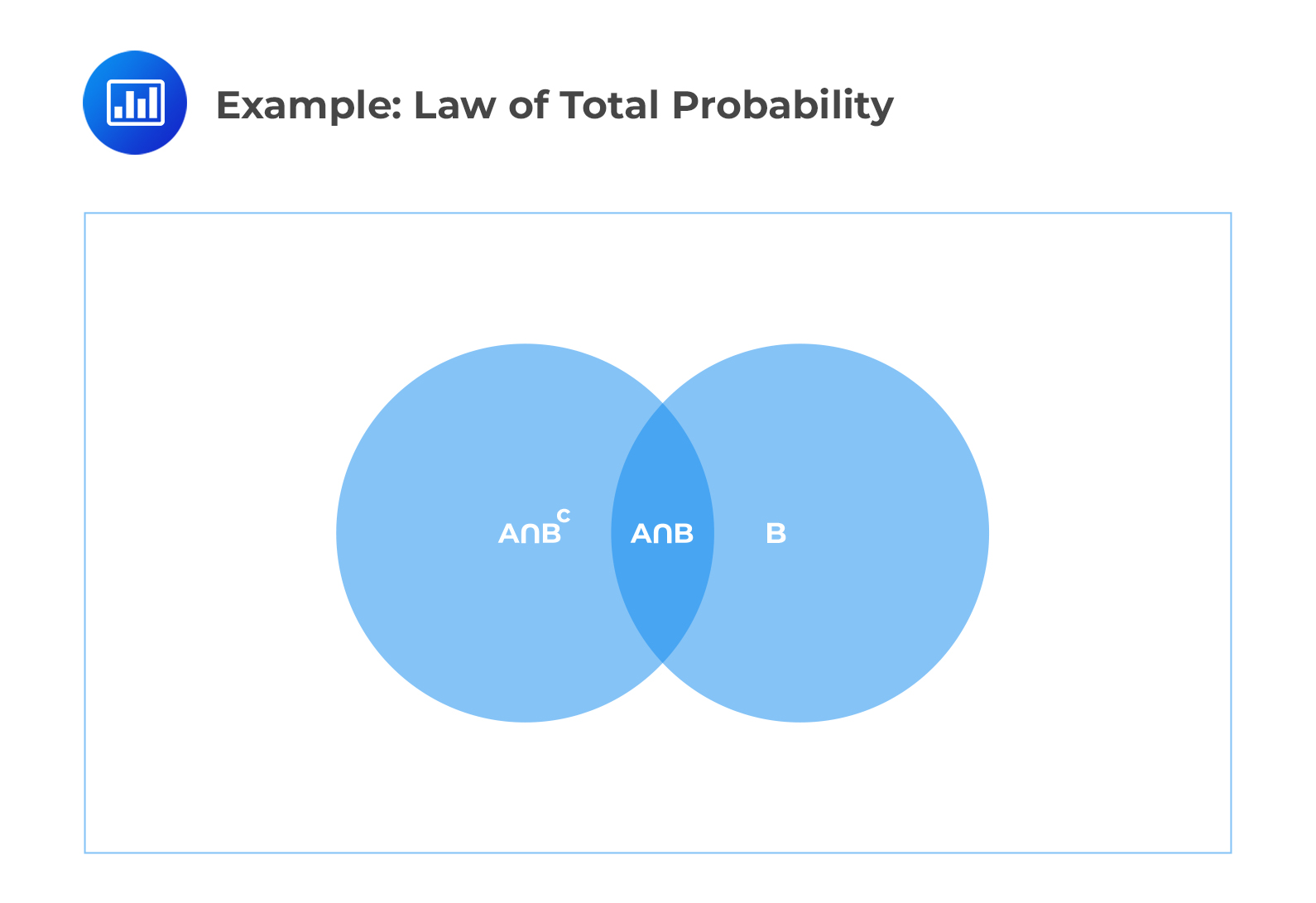Note that  \(B^c\) (also be written as \(B’\)) is the complement of an event B.

Therefore,

$$P(A)=P(A\cap B)+P(A\cap B^c)$$

Recall the conditional probability that:

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

So that:

$$P(A\cap B)=P(B)\bullet P(A|B)$$

 Similarly,

$$P(A\cap B^c)=P(B^c)\bullet P(A|B^c)$$

Thus,

$$ P\left( A \right) =P\left( A|B \right) \bullet  P\left( B \right) +P\left(A|B^c \right)\bullet \left( P\left( B^c \right) \right) $$

At this point, we can write the expression for \(P(B|A)\) as:

$$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{P(A)\bullet P(A|B)}{P\left( A|B \right) \bullet P\left( B \right) +P\left(A|B^c \right)\bullet \left( P\left( B^c \right) \right)}$$

The last expression is referred to as Bayes’ Theorem. 

Similarly,

$$P(B^c |A)=\frac{P(A\cap B^c)}{P(A)}=\frac{P(A)\bullet P(A|B^c)}{P\left( A|B \right) \bullet  P\left( B \right) +P\left(A|B^c \right)\bullet \left( 1-P\left( B \right) \right)}$$

Definition: Bayes’ Theorem

If \(E\) is an event and \(A_1 , A_2 ,…, A_3\) are the partition of a sample space, then:

$$\begin{align} P(A_i |E)&=\frac{A_i \cap E}{P(E)}\\ &=\frac{P(A_i)\bullet P(E|A_i)}{P(A_1)\bullet P(E|A_1)+P(A_2)\bullet P(E|A_2)+\cdots +P(A_n)\bullet P(E|A_n)} \end{align}$$

Consider the following examples:

Example: Law of Total Probability

In a given population of students, 25% play baseball, and 30% play basketball. Also, the probability of a student playing baseball given that they also play basketball is 10%.

Calculate the probability that a student plays baseball given that they do not play basketball.

Solution

Let event \(A\) be “plays baseball” and event \(B\) be “plays basketball.” Using the law of total probability, we have:

$$ \begin{align} P\left( A \right) & =P\left( A|B \right) \bullet P\left( B \right) +P\left(A|B^c\right)\bullet \left( 1-P\left( B \right) \right) \\ 0.25 &= 0.10 \bullet 0.30 + x \left(1-0.30 \right) \\ 0.22 &= x  \left(0.70 \right) \\ x &= \frac{0.22}{0.70} = 0.314 \ or \ 31.4\%  \end{align} $$

Example: Bayes’ Theorem

An insurance company deals with three insurance policies: 40% of life insurance, 25% of car insurance, and 35% of health insurance. The probability that a life insurance policyholder will file a claim in a given year is 0.50. The probability that a car insurance policyholder will file a claim in a given year is 0.20. Lastly, the probability that a health insurance policyholder will file a claim in a given year is 0.10.

At the course of this year, a policyholder files a claim.

Calculate the probability that the claim comes from the car insurance policyholder.

Solution

Let:

\(L\) = proportion of life insurance policyholders.

\(R\) = proportion of car insurance policyholders.

\(H\) = proportion of health insurance policyholders.

\(C\) = event that a claim is made.

From the information given in the question, we have:

$$ P(L) = 0.40,\  P(R) = 0.25,\ P(H) = 0.35 $$

Also, we have:

$$ P(C|L) = 0.50,\  P(C|R) = 0.20,\ P(C|H) = 0.10 $$

We need, \(P(R|C)\). Using the Bayes’ theorem, we know that:

$$\begin{align}P(R|C)&=\frac{P(R)\bullet P(C|R)} {P(R)\bullet P(C|R)+P(L)\bullet P(C|L)+P(H)\bullet P(C|H)}\\ &=\frac{0.25\times 0.20}{0.25\times 0.20+0.40\times 0.50 +0.35\times 0.10}\\ &=0.17543 \approx 17.54\%\end{align}$$

Learning Outcome

Topic 1.g: General Probability – State Bayes Theorem and use it to calculate conditional probabilities.