Define set functions, Venn diagrams, sample space, and events & define probability as a set function on a collection of events and state the basic axioms of probability.

1. What Is Probability?

   In mathematics, probability is the branch that deals with numerical descriptions of the likelihood that events will occur or that propositions are true. Probability is a number between 0 and 1, with 0 representing impossibility and 1 representing certitude (certainty). The higher the probability of an event, the more likely it is that the event will occur. Probabilities can be determined via two methods: counting and relative frequency.

   Counting

   Counting can be used to estimate probabilities in a wide variety of situations. For example, counting is used to solve problems in gambling that involves dice and cards. For example, let’s say you’re rolling a fair six-sided die labeled 1, 2, 3, 4, 5, and 6. The probability that you will roll a number less than 4 is 3/6 since there are three outcomes that are less than 4 (1,2, and 3) and there are six possible and equally likely outcomes. The probability approach used in this approach is summarized as follows:

   $$ \text{Probability of event}, P(E) = \frac {\text{Number of favorable outcomes}}{\text{Total Number of outcomes}} $$

   Question 1.1

   There are 12 pillows in a bed, 5 are white, 3 are green, 2 are yellow, and 2 are blue. What is the probability of picking a white pillow?

   Solution

   The probability is equal to the number of white pillows in the bed divided by the total number of pillows, i.e., 5/12

   Relative Frequency

   A relative frequency probability is found on the basis of experiments or trials. When examining the relative frequency of an event during an experiment, we consider how many times the event occurs as a proportion of the total number of trials:

   $$ \text{Probability of event}, P(E) = \frac {\text{Number of favorable outcomes in n trials}}{n} $$

   For example, let’s say you’re tossing a fair coin. In this case, you cannot determine the probability of tossing a tail by counting. However, you can estimate the probability by tossing the coin a large number of times and then count the number of tails. If you toss the coin 1000 times and observe 550 tails, your best estimate of the probability of a tail on one toss is 550/1000 or 0.55.

   Question 1.2

   James asks some people in his town about their dietary preferences and records the results in the table below:

   $$ \begin{array}{c|c} \textbf{Dietary Preference} & \textbf{Frequency} \\ \hline \text{Vegetarian} & 60 \\ \hline \text{Vegan} & 30 \\ \hline \text{Other} & 60 \end{array} $$

   What’s the relative frequency of someone in the town being vegetarian? If there are 10,000 people in James’ town, find an estimate for the number of people in this town who are vegetarian.

   Solution

   Firstly, we need the total number of trials:

   $$ \text{trials} = 60 + 30 + 60 = 150 $$

   Now, using the formula above,

   Relative frequency = \(\frac {60}{150} = \frac {4}{10} \text{ or } 0.4\)

   Our Solution suggests that if we picked someone from James’ town at random, there would be a 0.4 chance that they are vegetarian. Thus,

   Estimated no. of vegetarians = 0.4 × 10,000 = 4,000

2. The Language of Probability; Sets, Sample Spaces and Events

   When evaluating probabilities by counting outcomes of a probability experiment, it is imperative that all outcomes be identified. That’s because the person analyzing the data may not be familiar with the phenomenon under evaluation. A person who is not familiar with dice, for example, might not know that a single die can produce 1,2,3, 4, 5, or 6. There is no way such a person could figure out the probability of rolling a 3 with a single die. In order to conduct a well-defined probability experiment, all possible outcomes must be specified. This brings us to set theory – the branch of mathematics that deals with the properties of well-defined collections of objects. Let’s now look at the basic ideas of set theory.

   Definition 2.1 Set

   A set is a collection of distinct objects, called elements or members of the set.

   Example 2.1.1

   1. The possible outcomes of the rolling of a die – 1, 2, 3, 4, 5, and 6 – make up a set, and each of these outcomes are elements or members of the set.
   2. A list of odd numbers between 1 and 10 make up a set, i.e., 1, 3, 5, 7, and 9
   3. We could create a set of all the reference materials recommended for Exam P.

   There are a few things to note about sets. First, a set is usually enclosed in curly brackets {}. Second, the order is not important. This means that {1, 2, 3} is equivalent to {1, 3, 2} or {3, 2, 1}. The symbol ∈ means “is an element of.” For example,

   Let C = {1, 2, 3}

   To notate that 1 is member of the set, we’d write 1 ∈ C.

   In addition, a set that has no elements, { }, is called an empty set and is usually notated ∅.

   Definition 2.2 Subset

   A subset of a set C is any other set that contains only elements from the set C, but may not contain all the elements of C.

   If D is a subset of C, we write \(D \subseteq C\).

   Alternatively, if B is a subset of A, we write \(B \subseteq A\)

   A power set contains all the subsets of a given set, including the empty set. The number of elements of the power set is given by \(2^n\). You can think of the power set as a placeholder for all the subsets of a given set. In other words, a power set is made up of all of the subsets of a set.

   Example 2.2.1

   Given C = {1, 2, 3}

   Power set of C = {{1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}, {∅}}

   As can be seen the power set has \(2^n\) elements (i.e., \(2^3 =8\))

   A proper subset is a subset that does not contain the same number of elements as the original set.

   Definition 2.3. Sample Space

   The sample space, S, for a probability experiment is the set of all possible outcomes of the experiment.

   Example 2.3.1

   Let’s say we want to roll a six-sided die and are interested in the number facing up.

   The sample space is S = {1, 2, 3, 4, 5, 6}

   Example 2.3.2

   Consider a life insurance company concerned with the probability that an insured will die at some point in the following year.

   The sample space is S = {Death, Survival}

   Example 2.3.3

   Assume we’ve got a coin and our interest is the side facing up after a toss.

   The sample space is S = {H, T}

   What if we’re tossing two coins instead of just one?

   The sample space is \(S = \left\{(H_1, H_2), (H_1, T_2), (T_1, H_2), (T_1, T_2) \right\}\)

   Example 2.3.4

   The most common way for homeowners to buy their homes is to take out a mortgage loan, which is then repaid through monthly payments. If the homeowner so desires, they can usually pay off the mortgage loan early. They might do so because they want to move to a new location, because interest rates have gone down, or even because they’ve won a lottery. Since lenders may lose or gain money when a loan is repaid early, they may want to find out how likely it is to happen.

   The sample space for a lender who wants to know if the loan will prepay in the next month is S = {prepayment, no prepayment}.

   Definition 2.4 An Event

   An event is a subset of the sample space S of an experiment. In other words, an event is

   a set consisting of possible outcomes of the experiment.

   Example 2.4.1

   Let’s say we want to roll a six-sided die and are interested in the probability of getting a 6.

   The sample space is S = {1, 2, 3, 4, 5, 6}, and the event is the subset E = {6}

   Example 2.4.2

   There have been 50 life insurance policies sold by an insurance company. The company is interested in the probability that there will be at most seven death benefit claims over the next one year.

   The sample space is S = {1, 2, 3, …, 49, 50}, and the event is the subset E = {0, 1, 2, 3, 4, 5, 6, 7}

   Example 2.4.3

   Two coins are tossed and we’re interested in the probability that there will be at least one tail.

   The sample space is \(S = \left\{ (H_1, H_2), (H_1, T_2), (T_1, H_2), (T_1, T_2) \right\} \)

   The event is the subset \(E = \left\{(H_1, T_2), (T_1, H_2), (T_1, T_2) \right\}\)

   Definition 2.5 The Universal Set

   The universal set, U, is the set of all elements under consideration. It consists of elements of all the related sets, without any repetition of elements.

   Example 2.5.1

   Assume we’ve got two sets, A and B, where \(A = \left\{1, 2, 3 \right\}\) and \(B = \left\{ 1, 2, 7, 8, 11 \right\}\)

   The universal set associated with these two sets is given by \(U = \left\{1, 2, 3, 7, 8, 11 \right\}\)

   Notice that there’s no repetition in the universal set.

    

3. Set Notation

   Set notation is used to define the elements and properties of compound events using symbols. Compound events are those events that involve the probability of more than one outcome occurring together. For example, on a given day, we might be interested in the probability that it rains and the bus arrives late. Alternatively, we may want to find the probability that an investor buys a stock or bond given certain conditions.

   Compound events are diagrammatically represented using a tool called the Venn diagram. In a Venn Diagram, the entire sample space is represented by a rectangular region, and a circular/oval region inside the rectangle represents an event.

   Let’s look at the most commonly used notation when dealing with compound events and how they can be represented in Venn diagrams.

   3.1 Union of Events

   The union of two events is the set of all outcomes that are in either one or both of the two events. The symbol for union is \(\cup\), and is associated with the word “or.” For example, \(\left\{1, 2, 3 \right\} \cup \left\{3, 4 \right\} = \left\{1, 2, 3, 4 \right\}\)

   For any two events A and B, \(A \cup B\) is defined as the union of events A and B and includes all outcomes that are either in A or B or in both A and B. The union of A and B in the diagram below includes the entire shaded region.

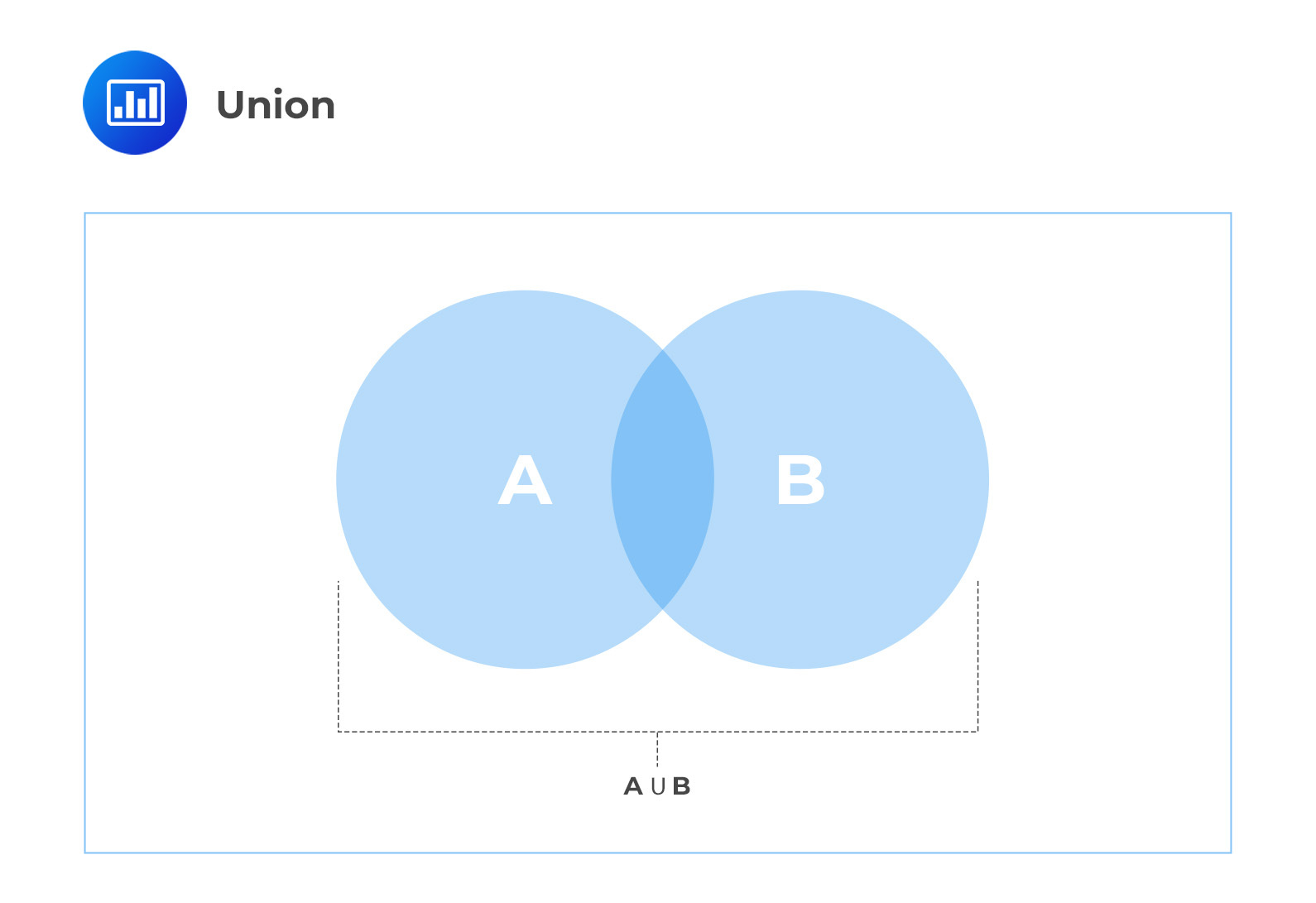   Example 3.1.1

   During a performance evaluation, students in a class are selected in such a way that every student has the same chance of being picked. A denotes the event “the student needs help in Arts” and B denotes the event “the student needs help in Biology.” The information given is that P(A) = 0.34, P(B) = 0.56, and the two events are mutually exclusive.

   Determine the probability that a student picked at random needs help in Arts or Biology.

   Solution

   Since the two events are mutually exclusive, i.e., there’s no chance both will occur at the same time because the occurrence of one precludes the occurrence of the other,

   $$ P(A \cup B) = P(A) + P(B) = 0.34 + 0.56 = 0.90 $$

   If the events weren’t mutually exclusive, the solution would be a bit different as we shall see shortly.

   3.2 Intersection of Events

   The intersection of events A and B, denoted A∩B, is the collection of all outcomes that are elements of both of the sets A and B. It’s associated with the use of the word “and” to describe the joint event of A and B. The intersection of A and B in the diagram below is shown as the darker shaded region and labeled as \(A \cap B\)

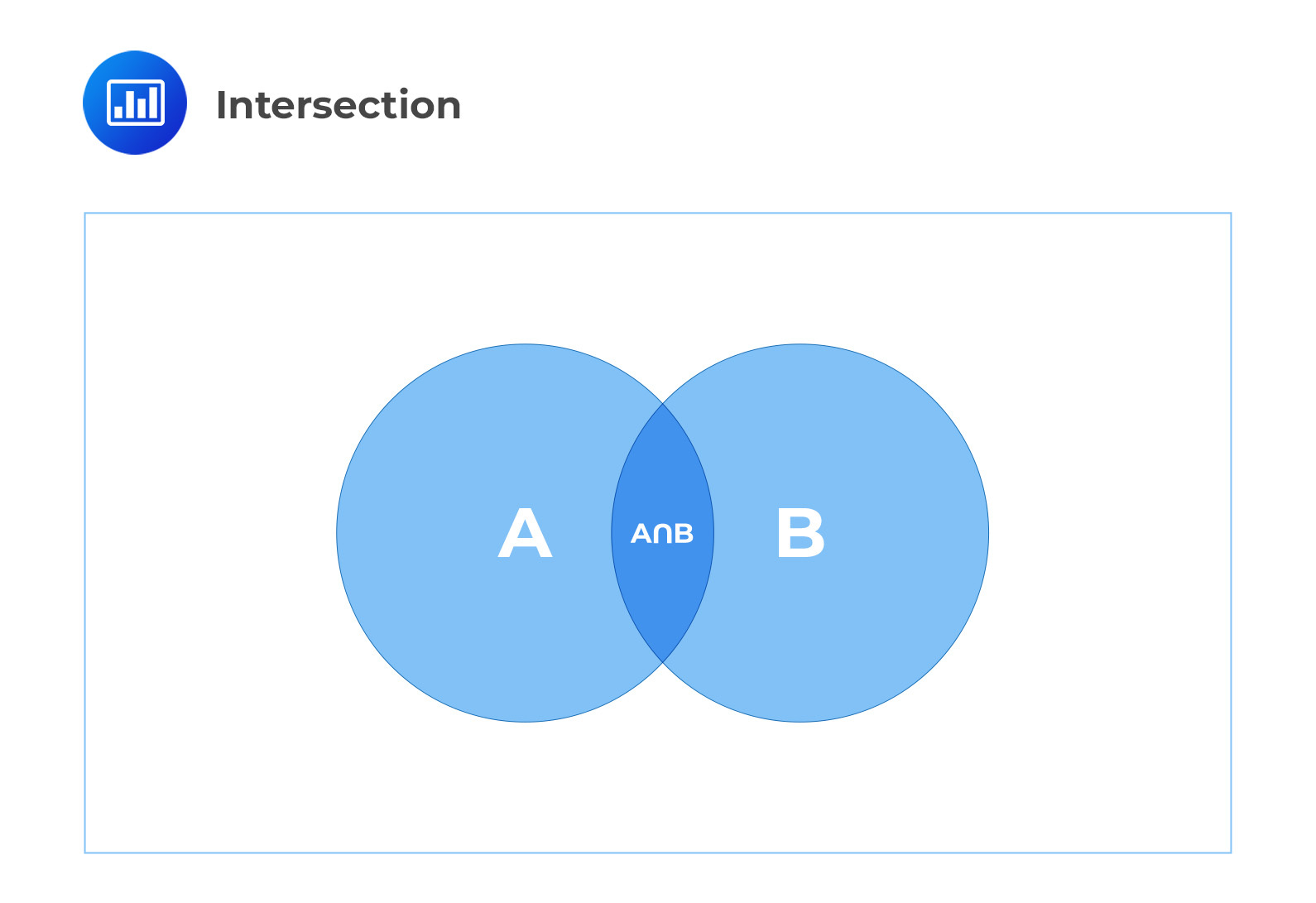   Example 3.2.1

   In an experiment of rolling a single die, two events, M and N, are defined such that M is the event “the number rolled is odd” and N is the event “the number rolled is greater than two.”

   How do we find the intersection \(M \cap N\)

   The sample space is \(S = \left\{1, 2, 3, 4, 5, 6 \right\}\)

   The intersection is described by “the number rolled is odd and is greater than two.” The only numbers between one and six that are both odd and greater than two are three and five.

   Thus, \(M \cap N = \left\{3, 5 \right\}\)

   3.3 complements

   The complement of an event contains all outcomes not included in the event. To be more specific, the complement of an event A in a sample space \(S\), denoted \(A^c\), is the collection of all outcomes in S that are not elements of the set A. The other notation commonly used to represent complements is \(A^\prime\).

   \(A^\prime\) is the darker region in the diagram shown below.

   Example 3.3.1

   Let the universal set, \(U = \left\{1, 2, 3, a, b, c\right\}\). Sets A and B are defined such that \(A = \left\{1, 2 \right\}\) and \(B = \left\{2, b, c \right\}\). How do we find \(A^c\)?

   The complement of an event A is the collection of all outcomes in \(\cup\) that are not elements of the set A:

   Thus, \(A^c = U – A = \left\{1, 2, 3, a, b, c \right\} – \left\{1,2 \right\} = \left\{3, a, b, c \right\}\)

   Example 3.3.2

   Let’s once again leverage our experiment of rolling a single die, where two events, M and N, are defined such that M is the event “the number rolled is odd” and N is the event “the number rolled is greater than two.” What if we were to find the complements of each?

   The sample space is \(S = \left\{1, 2, 3, 4, 5, 6 \right\}\), and the corresponding sets of outcomes are \(M = \left\{1, 3, 5 \right\}\) and \(N = \left\{ 3, 4, 5, 6 \right\}\)

   The complement of \(M, M^c = \left\{2, 4, 6 \right\}\)

   The complement of \(N, N^c = \left\{1, 2 \right\}\)

   Describing the complements in words, \(M^c\) would be the event “the number rolled is not odd” and \(N^c\) would be the event “the number rolled is not greater than two.” But we could also go with the relatively straightforward alternatives: \(M^c\) is the event “the number rolled is even” and \(N^c\) is the event “the number rolled is less than three.” There are many paths to the top of the mountain, but the view is always the same!

   3.4 Mutually Exclusive Events

   Events A and B are mutually exclusive if they have no elements in common (cannot both occur at once). The occurrence of one precludes the occurrence of the other. Mutually exclusive events are also known as disjoint events.

   If events A and B are mutually exclusive, then \(A \cap B = \emptyset \) and \(P(A \cap B) = 0\)

   Events A and B in the diagram below are considered mutually exclusive.

   

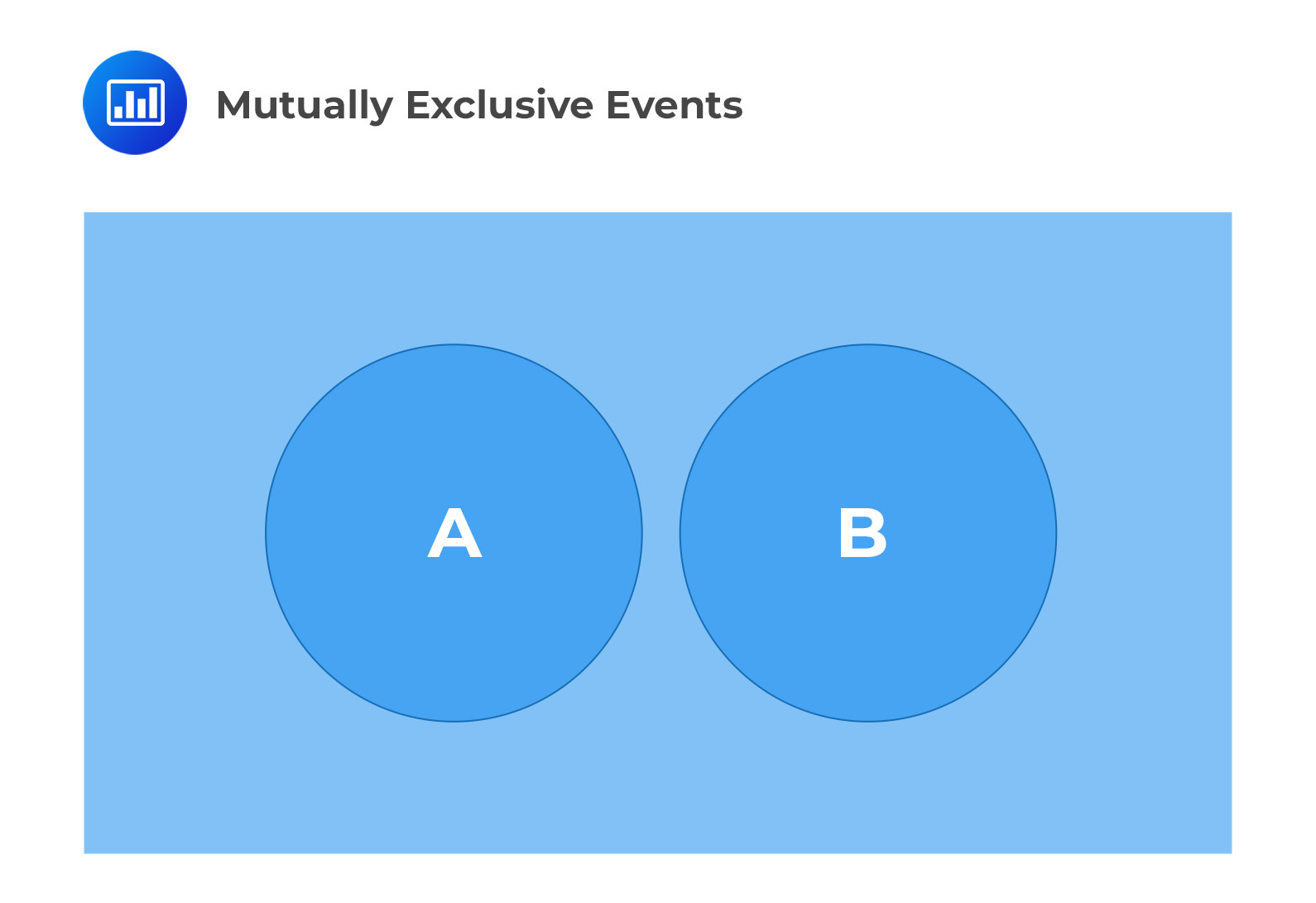
4. Properties of Set Functions

   4.1 Commutative Property

   This commutative property states that when the order of elements in union or intersection operations is changed, the results of the operation do not change.

   $$ \begin{align*} A \cap B & = B \cap A \\ A \cup B & = B \cup A \end{align*} $$

   4.2 Associative Property

   According to the associative property, when the parentheses’ position is changed in any operation that involves union or intersection, then the resultant set will not be affected.

   $$ \begin{align*} A \cup (B \cup C) & = (A \cup B) \cup C \\ A \cap (B \cap C) = (A \cap B) \cap C \end{align*} $$

   4.3 Distributive Property

   The distributive property states that union and intersection are distributive over intersection and union, respectively.

   $$ \begin{align*} A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \\ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \end{align*} $$

   4.4 Idempotent Property

   The idempotent property states that intersection and union of any set with itself revert the same set

   $$ \begin{align*} A \cup A & = A \\ A \cap A & = A \end{align*} $$

   4.5 Identity Property

   The identity property states that the union of any set with an empty set returns the original set. Similarly, the intersection of a set with the universal set reverts to the original set.

   $$ \begin{align*} A \cup \emptyset & = A \\ A \cap U & = A \end{align*} $$

   4.6 Complement Property

   According to the complement property, the union of a set A and its complement A’ gives the universal set \(\cup\). What’s more, the intersection of a set with its complement returns the empty set.

   $$ \begin{align*} A \cup A^C & = U \\ A \cap A^C & = \emptyset \end{align*} $$

   4.7. De Morgan’s Law

   De Morgan’s Law states that the complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements.

   $$ \begin{align*} (A \cup B)’ & = A’ \cap B’ \\ (A \cap B)^C & = A^C \cup B^C \end{align*} $$

5. Axioms of Probability

   Probability theory is based on three fundamental axioms:

   Axiom 1

   The probability of an event is always between 0 and 1

   Axiom 2

   Probability of the sample space S is P(S)=1

   Axiom 3

   The probability of any event containing any number of disjoint (mutually exclusive) outcomes is the summation of their individual probabilities.

   $$ P(A1 ∪ A2 ∪ A3⋯)=P(A1) + P(A2) + P(A3) + ⋯ $$

   Example 5.1

   An election for president features five candidates – A, B, C, D, and E. Based on a recent poll, it’s estimated that candidate B has a 40 percent chance of winning the election, while C’s and D’s chances of winning stand at 15 percent. How do we find the probability that B or C or D win the election?

   $$ \begin{align*} P(B \text{ wins or } C \text{ wins or } D \text{ wins}) & = P({B \text{ wins}} ∪ {C \text{ wins}}) \cup {D \text{ wins}}) \\ & = 0.4 + 0.15 + 0.15 = 0.70 \end{align*} $$

Learning Outcome

1.a Topic: General Probability – Define set functions, Venn diagrams, sample space, and events. Define probability as a set function on a collection of events and state the basic axioms of probability.