Explain and apply the concepts of random variables

Definitions:

Variable: In statistics, a variable is a characteristic, number, or quantity that can be measured or counted.

Random variable: A random variable (RV) is a variable that can take on different values, each with a certain probability. It essentially assigns a numerical value to each outcome of a random experiment. Random variables are often denoted by capital letters, say X, Y, or Z. Random variables can be either discrete or continuous.

Discrete Random Variables

A discrete random variable is a numerical variable whose range of possible values is drawn from a specified and countable list. In other words, a discrete random variable takes distinct countable numbers of positive values in the sample space, and it is not possible to get values between the numbers.

For a discrete random variable X, we define probability mass function (PMF) as a mathematical function that describes the relationship between the random variable, X, and the probability of each value of X occurring Mathematically, the PMF of X can be expressed as follows:

$$
f(x)=P(X=x) $$

Let's look at an example.

When two coins are tossed simultaneously, the possible outcomes for the number of heads appearing can be 0 (when both coins show tails), 1 (when one coin shows a head and the other shows a tail), or 2 (when both coins show heads). In this scenario, the PMF would assign a probability to each of the possible outcomes: 0, 1, or 2 heads. Specifically, there's a 1/4 chance of getting 0 heads (TT), a 1/2 chance of getting 1 head (HT or TH), and a 1/4 chance of getting 2 heads (HH).

$$ \begin{array}{c|c|c|c}
\text{Number of heads, x} & 0 & 1 & 2 \\ \hline
{f(x) = P(X = x)} & 0.25 & 0.5 & 0.25
\end{array} $$

Graphically, the probability mass function is often represented by plotting the probability values, \(f(x_i)\) on the y-axis against the corresponding values of \(x_i\) on the x-axis. For example, the graph below illustrates a probability mass function:

$$ f(x)=
\left\{\begin{matrix}
0.2, & x=1,4 \\
0.3 & x=2,3 \\
\end{matrix}\right. $$

The probability mass function has the following properties:

1. \(f \left(x \right) > 0,\quad x € S;\) meaning all individual probabilities must be greater than zero.
2. \({ \Sigma }_{ x\in S }f\left( x \right)=1; \) meaning the sum of all individual probabilities must equal one.
3. \(P\left( X\in A \right) ={ \Sigma }_{ x\in A }f\left( x \right) \),where \(A\subset S; \) meaning the probability of event \(A\) is the sum of the probabilities of the values of \(X\) in \(A\).

Important note: In the context of probabilities and random variables, the distinction between “x” in lowercase and “X” in uppercase is significant. Generally, “X” in uppercase represents a random variable, which is a function that maps outcomes from a sample space to numerical values. It is a theoretical construct used to describe uncertain or variable quantities. On the other hand, “x” in lowercase usually denotes a specific realization or observed value of that random variable “X”. For instance, if “X” represents the number of heads when flipping a pair of coins simultaneously, “x” could be a specific outcome, such as getting two heads.

Example 1: Discrete Random Variables

Suppose a customer care desk receives calls at a rate of 3 calls every 4 minutes. Assuming a Poisson process, what is the probability of receiving 4 calls during a 16-minutes period?

Solution

The Poisson distribution gives the probability of a number of events happening in a fixed interval of time or space, given the average number of times the event occurs over that period.

For a Poisson random variable X:

$$ P(X=k)=\frac {(\lambda^k e^{(-\lambda)})}{k!} $$

In this case,

$$ \begin{align*} \lambda & =\frac{3}{4}\times16=12 \\
\Rightarrow P\left(X=4\right) &=\frac{{12}^4e^{-12}}{4!} =0.0053 \end{align*} $$

Example 2: Discrete Random Variables

Consider an experiment of rolling a fair 6-sided die. Let X be the random variable representing the number rolled.

1. Determine the probability mass function.
2. Calculate the probability of getting a “3” and a “4”.
3. Calculate the probability of getting a “4” or a “6”.

Solution

1. The probability mass function of X is as given in the table below:

   $$ \begin{array}{c|c}
   X & P(X=x) \\ \hline
   1 & \frac {1}{6} \\ \hline
   2 & \frac {1}{6} \\ \hline
   3 & \frac {1}{6} \\ \hline
   4 & \frac {1}{6} \\ \hline
   5 & \frac {1}{6} \\ \hline
   6 & \frac {1}{6}
   \end{array} $$

2. The probability of getting a “3” and a “4”:

   $$ P(X=3 \text{ and } X=4)=\frac {1}{6} \times \frac {1}{6}= \frac {1}{36} $$

3. The probability of getting a “4” or a “6”:

   $$ P(X=3 \text{ or } X=6)= \frac {1}{6}+ \frac {1}{6}= \frac {2}{6}= \frac {1}{3} $$

Example 3: Discrete Random Variables

Probability that an SME will survive the financial crisis resulting from to an ongoing pandemic is 0.6. Calculate the probability that at least 10 out of a group of 14 SMEs will survive the pandemic.

Solution

Let \(X\) be the random variable for the number of SMEs that survive the pandemic.

From the given information, \(X \sim Bin(14,0.6)\)

We know that for a binomial random variable:

$$ \begin{align*} P(X=x) & =\binom{n}{x} p^X (1-p)^{n-x} \\
P(X \ge 10) & = P(X = 10) + P(X = 11) + P(X = 12) + P(X = 13) + P(X = 14) \\
& = \binom{14}{10} (0.60)^{10} (1-0.60)^{14-10}+ \binom{14}{11} 0.60^{11} (1-0.60)^{14-11} \\ & + \binom{14}{12} 0.60^{12} (1-0.60)^{14-12}
+ \binom {14}{13} 0.60^{13} (1-0.60)^{14-13} \\ & +\binom{14}{14} 0.60^{14} (1-0.60)^{14-14} \\
& = 0.15495 + 0.08452 + 0.03169 + 0.007314 + 0.0007836 \\
& = 0.2793
\end{align*} $$

Example 4: Discrete Random Variables

A basket contains 4 oranges and 6 mangoes. Fruits are randomly selected, with replacement until a mango is obtained. Find the probability that exactly 3 draws are needed.

Solution

From the information given, the number of draws is a geometric random variable.

$$ \Rightarrow P(X=n)=(1-p)^{n-1} p, \ \ \ \ n=1,2,\dots $$

The probability of success in this case is:

$$ p=\frac {6}{10}=0.6 $$

Therefore, the probability of exactly 3 draws is given by:

$$ P(X=3)=(1-0.6)^{3-1} 0.6=0.096 $$

Cumulative Distribution Function for Discrete Random Variables

The cumulative distribution function (CDF) is a fundamental concept in probability theory and statistics which provides a way to describe the probability distribution of a random variable by specifying that the random variable is less than or equal to a given value.

For a random variable \(X\), the cumulative distribution function \(F(X)\) can be expressed mathematically as:

$$ F(x) = P (X \le x) ,-\infty \lt x \lt \infty $$

The cumulative distribution function \(F\) for a discrete random variable can be expressed in terms of \(f(a)\) as:

$$ F(a)=\sum_{\forall x \le a} f(x) $$

Note that in this case, the sum is taken over all values of \(x\) that are less than or equal to \(a\).

For a discrete random variable \(X\) whose possible values are \(x_1,x_2,x_3,\dots\) for all \(x_1 \lt x_2 \lt x_3 \lt \cdots\), the cumulative distribution function, \(F(x)\) is a step function. As such, \(F\) is constant in the interval \([x_{i-1},x_i]\) and exhibits a “jump” or discontinuity of \(f(x_i)\) at \(x_i\).

Now, let's work through an example to illustrate the computation and graphing of a cumulative distribution function:

Example: Graph of Cumulative Distribution Function

Let \(X\) be the random variable for the number of tornadoes occurring in a given year. Suppose that \(X\) has the following probability mass function:

$$ f(x) = \left\{\begin{matrix}
0.2, & x=1,4 \\ 0.3, & x=2,3
\end{matrix}\right.
$$

1. Find the cumulative distribution function of \(X\).
2. Plot the graph of the cumulative distribution function of \(X\).

Solution

First, we construct a table showing the values of \(X_i\), \(f(x_i)\) and \(F(x_i)\):

$$ \begin{array}{c|c|c}
X_i & f(x_i) & F(x_i) \\ \hline
1 & 0.2 & 0.2 \\ \hline
2 & 0.3 & 0.5 \\ \hline
3 & 0.3 & 0.8 \\ \hline
4 & 0.2 & 1.0
\end{array} $$

From the table, we can see that the cumulative probabilities, \(F(x_i)\) increase (accumulate) as we move from left to right along the ordered values of \(x\). The cumulative distribution function, \(F(x_i)\) can be represented as follows:

$$ F(x_i )= \left\{\begin{matrix} 0, & x \lt 1 \\ 0.2, & 1 \le x \lt 2 \\ 0.5, & 2 \le x \lt 3 \\ 0.8, & 3 \le x \lt 4 \\ 1, & x \ge 4 \end{matrix}\right. $$

Plotting the graph of the cumulative distribution function \(F(x_i)\), we get a step function with jumps at each \(x_i\) value, reflecting the cumulative probabilities associated with each value:

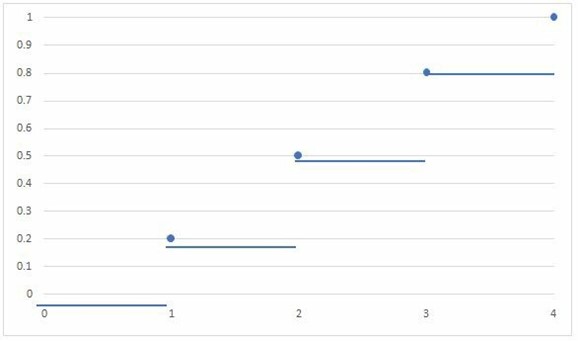
In the graph above, the step-wise nature of the function is clearly visible, with the jumps occurring \(X=1\), \(X=2\), \(X=3\), and \(X=4\). We can also see that the values of the function are increasing as we move along the x-axis.

Continuous Random Variable

A continuous random variable is a random variable that can take on an infinite number of possible values within a given range.

Let \(X\) be a continuous random variable and \(f(x)\) be a non-negative function defined on the interval \((-\infty,\infty)\). For any real values \(R\), the probability of \(X\) falling within the range defined by \(R\) can be calculated by integrating \(f(x)\) over that range:

$$ Pr⁡(X \in R)=\int_R f(x)dx $$

The probability density function, \(f(x)\), of a continuous random variable is a differential equation with the following properties:

1. \(f(x) \ge 0\): meaning the function (all probabilities) is always greater than zero
2. \(\int_{-\infty}^\infty f(x)dx=1\): meaning the sum of all the possible values (probabilities) is one.

Note that for a discrete random variable, the probability mass function (PMF) assigns the probability of the random variable taking on specific discrete values. On the other hand, for a continuous random variable, the probability density function (PDF) does not directly provide probabilities for specific outcomes. Instead, it provides the probability of the random variable falling within a certain range of values.

Therefore, for continuous random variables, we can get the desired probability value from a given probability density function using the following function:

$$ P(X \lt a)=P(X \le a)=f(a)=\int_{-\infty}^a f(x)dx $$

Also, note that for \(R=[a,b]\)

$$ P(a \le X \le b)=\int_a^b f(x)dx $$

The graph of \(P(a \le X \le b)\) is as shown below:

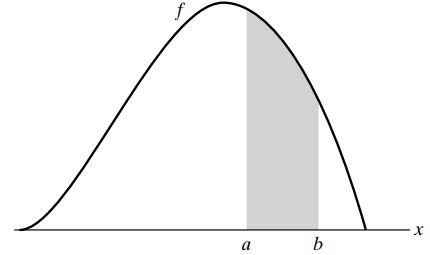
Also, it is important to note that the probability of any individual value of a probability density function is zero, as shown in the formula below:

$$P\left(X=a\right)= \int_{a}^{a}{f\left(x\right)} dx=0$$

Example: Calculating Probability from a PDF

Given the following probability density function of a continuous random variable:

$$ f\left( x \right) =\begin{cases} { x }^{ 2 }+c, & 0 < x < 1 \\ 0, & \text{otherwise} \end{cases} $$

1. Calculate C.

   Solution

   Using the fact that:

   $$\begin{align*} \int_{-\infty}^{\infty}{f(x)dx} & =1 \\ \Rightarrow \int _{ 0 }^{ 1 }{ \left( { x }^{ 2 }+C \right) dx} & =1 \\ = { \left[ \frac { { x }^{ 3 } }{ 3 } +Cx \right] }_{ x=0 }^{ x=1 } & =1 \\ = \frac {{1}}{{3}} + C & = 1 \\ \therefore C & = \frac {{2}}{{3}} \end{align*}$$

2. Calculate \(P (X > {\frac {1}{2})}\)

   We know that:

   $$ \begin{align*} P\left(X > a\right) & = \int_{a}^{\infty}f\left(x\right)dx \\ \Rightarrow P\left(X > \frac{1}{2}\right) & =\int_{\frac{1}{2}}^{1}{(x^2+\frac{2}{3})dx} \\ & =\left[\frac{x^3}{3}+\frac{2}{3}x\right]_{x=\frac{1}{2}}^{x=1} \\ & =\left[\frac{1}{3}+\frac{2}{3}\right]-\left[\frac{1}{24}+\frac{1}{3}\right] \\ & =0.625 \end{align*}$$

The Cumulative Distribution Function – Continuous Case

Just like for discrete random variables, the cumulative distribution function of a continuous random variable, \(X\) can be defined as

$$ F(x) = P(X \le x) ,-\infty < x < \infty $$

However, while summation is applied for discrete calculations, integration is applied for continuous random variables. i.e.,

$$ F (x) =\int_{-\infty}^{x}f\left(x\right)dx $$

It is worth noting that the CDF for continuous random variables is an increasing function of x. This implies that the CDF increases as x increases or remains constant. Plotting the graph of the CDF of a continuous random variable exhibits a smooth and continuous curve contrary to the graph of CDF of step-wise discrete random variables that exhibit jumps.

Example: Cumulative Distribution Function-Continuous Case

Given the following PDF,

$$ f(x)= \begin{cases} x^2+c, & 0 < x < 1 \\ 0, & \text{otherwise} \end{cases} $$

Find the cumulative distribution function, \(F(x)\).

Solution

From the previous example, we had calculated that \(c=\frac{2}{3}\)

$$ \Rightarrow f(x)= \begin{cases} x^2+\frac{2}{3}, & 0 < x < 1 \\ 0, & \text{otherwise} \end{cases} $$

Therefore,

$$ F\left(x\right) = \begin{cases} \int_{-\infty}^x 0 \ dt=0, & \text{for } x < 0 \\ \int_{-\infty}^0 0 \ dt+ \int_0^x \left(t^2+\frac{2}{3} \right)dt=\frac{x^3}{3}+\frac{2}{3}x, & \text{for } 0 < x < 1 \\ \int_{-\infty}^{0} 0 \ dt+ \int_0^1 \left(t^2+\frac{2}{3}\right)dt+ \int_1^x 0 \ dt=1, & \text{for } x \ge 1 \end{cases} $$

Example: Cumulative Distribution Function-Continuous Case

A continuous random variable, \(X\), defined over the interval (0,3), has a probability density function, \(f_X (x)=2cx^5\).

Determine \(F_X(1)\)

Solution:

We first find the value of c.

We know that

$$ \begin{align*}
\int_{-\infty}^\infty f(x)dx & =1 \\
\Rightarrow \int_0^3 2cx^5 dx=c \left[ \frac {x^6}{3} \right]_0^3 & =1 \\
\Rightarrow c\left( \frac {3^6}{3} \right) &=1 \\
c & =243 \end{align*} $$

Now, the probability distribution function is given as:

$$ f_X (x)=\left\{ \begin{matrix} \frac {2}{243}x^5, & 0 \lt x \lt3 \\ 0, & \text{elsewhere} \end{matrix}\right. $$

Therefore,

$$ F_X (1)=P(X\le 1)=\int_0^1 \frac {2}{243} x^5 dx=0.0013717 $$

Learning Outcome

Topic 2. a: Univariate Random Variables – Explain and apply the concepts of random variables, probability, probability density functions, and cumulative distribution functions.