Calculate Probabilities Using Addition and Multiplication Rules

1. The Addition Rule

   The Addition Rule of Probability is a rule for determining is used to find the probability that event A or event B happens. It’s associated with the use of the conjunction “or.” For example,

   • We may want to find the probability of rolling a 3 or a 6 on a fair die
   • An insurance company might want to determine the probability that a claim comes from a make policyholder or the claim is greater than $5,000.

   There are two versions of the Addition Rule depending on whether the events involved are mutually exclusive (do not share elements) or non-mutually exclusive (share elements). Let’s see how each version looks like.

   1.1 The Addition Rule for Non-Mutually Exclusive Events

   Non-mutually exclusive events are those that can happen at the same time. In the language of probabilities, such events are said to have some elements in common. Examples include losing and scoring in a game of soccer, driving and listening to music, or going into labor during the day and giving birth to a girl. More practical examples within the field of finance and insurance include owning a home and having an active insurance policy, having a credit card while also servicing a car loan, or defaulting on premium payment and getting into an accident.

   When two events, A and B, are non-mutually exclusive, the Addition Rule tells us that the probability that A or B will occur is the sum of the probability that either event will happen minus the probability that both will happen:

   $$ P(A \cup B) = P(A) + P(B) − P(A \cap B) $$

   The last term, \(P(A \cap B)\), enters the equation twice, i.e., once in P(A) and once in P(B). As such, we must subtract it once so that it is not double-counted.

   A Venn diagram perfectly illustrates the idea of double counting. The intersection between A and B has to be subtracted when considering the probability of A or B.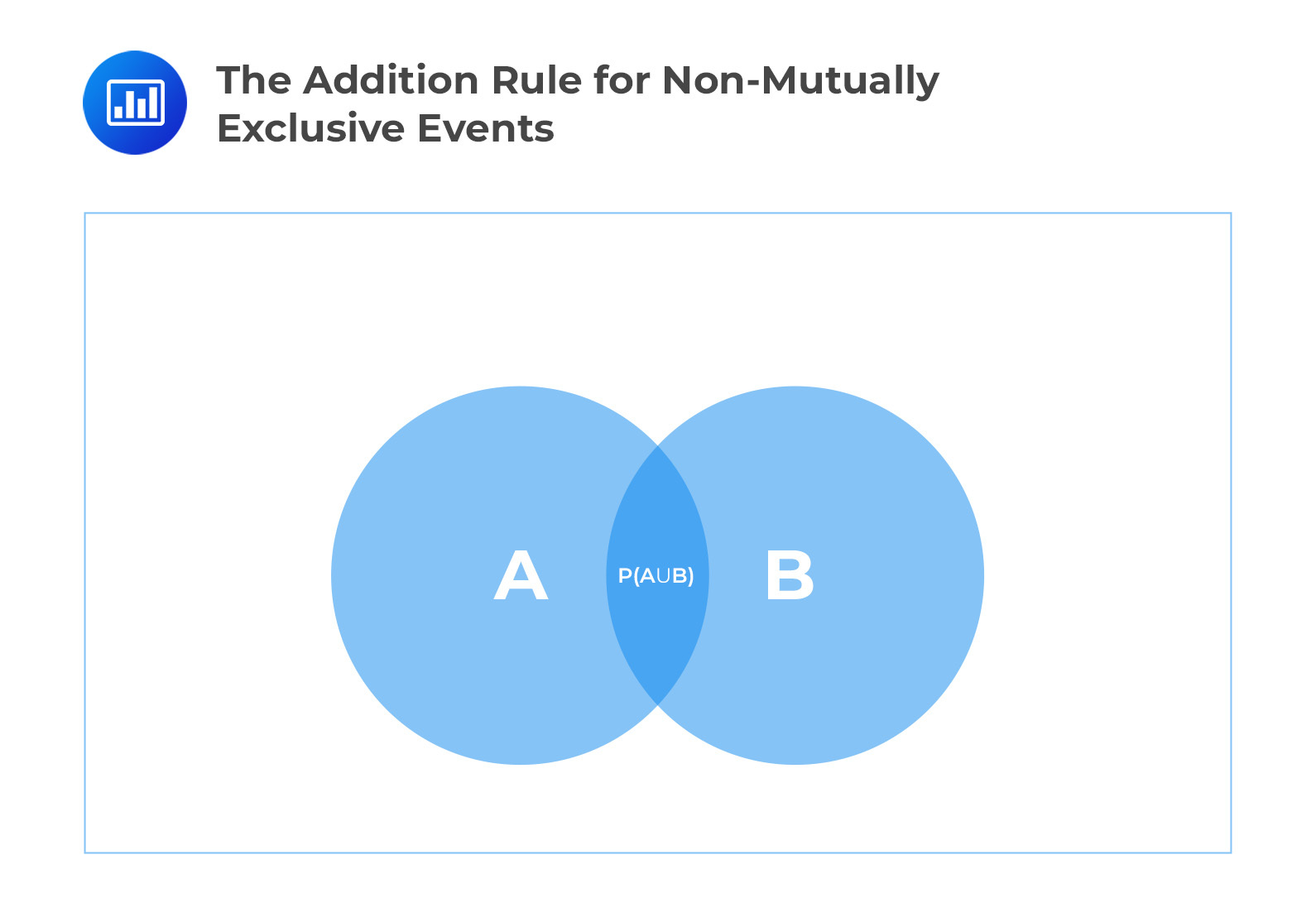Example 1.1.1

   Let’s say you’ve taken out a single card from a regular pack of cards. What would be the probability that the card is either an ace or heart?

   Let A be the event of picking an ace and B be the event of picking a heart.

   \(P(A) = \frac {4}{52}\) and \(P(B) = \frac {13}{52}\)

   \(P(A \text{ and } B) = \frac {1}{52}\)

   The two events are non-mutually exclusive because there’s always a chance that the card will be both an ace and heart.

   Thus,

   $$ \begin{align*} P(A \cup B) & = P(A) + P(B) − P(A \cap B) \\ & = \frac {4}{52} + \frac {13}{52} – \frac {1}{52} \\ & = \frac {16}{52} = \frac {4}{13} \end{align*} $$

   Note: In a standard deck of cards, there are four suites: hearts, clubs, spades, and diamonds. There are thirteen cards in each suite: an ace, a 2, a 3, a 4, a 5, a 6, an 8, a 9, a 10, a jack, a queen, and a king. Thus, the entire deck has 52 cards in total.

   Example 1.1.2

   The gender breakdown in a math class of 40 students is 25 boys to 15 girls. During the end-of-year exam, 12 boys and 5 girls made an A grade. If we were to pick a student at random from the class, what would be the probability of choosing a girl or an A student?

   Let G be the event of choosing a girl and A be the event of choosing an A student.

   \(P(G) =\frac {15}{40}\) and \(P(A) = \frac {17}{40}\)

   The probability of choosing a girl who has made grade A is \(\frac {5}{40}\), i.e.,

   \(P(G \text{ and } A) = \frac {5}{40} \)

   The two events are non-mutually exclusive because there’s always a chance that the student chosen will be both be a girl and an A student.

   Thus,

   $$ \begin{align*} P(G \cup A) & = P(G) + P(A) − P(G \cap A) \\ & = \frac {15}{40} + \frac {17}{40} – \frac {5}{40} \\ & = \frac {27}{40} \end{align*} $$

   Example 1.1.3

   A consulting firm employs 100 people. 51 of these have degrees in finance, 63 have degrees in economics, and 28 have degrees in both. What is the probability that an employee chosen at random has a degree in either finance or economics?

   Let F and E be the events that an employee has a degree in finance and economics, respectively.

   Our interest is \(P(F \cup E)\)

   $$ \begin{align*} P(F \cup E) & = P(F) + P(E) − P(F \cap E) \\ & = 0.51 + 0.63 – 0.28 \\ & = 0.86 = 86\% \end{align*} $$

   Note: Given three non-mutually exclusive events A, B, and C, the addition rule appears as follows:

   $$ \begin{align*} P(A \cup B \cup C) & = {P(A) + P(B) + P(C) – P(A \cap B) – P(B \cap C)} \\ & {- P(A \cap C) + P(A \cap B \cap C)} \end{align*} $$

   Question 1.1.1

   A life insurance company subjects potential policyholders to varying levels of medical evaluation depending on certain factors such as age and smoking status of an individual. The probability that a visit to the Life Office results in neither lab work nor referral to a specialist is 50%. Of those coming to the Life Office, 25% are referred to specialists and 35% require lab work.

   Calculate the probability that a visit to the Life Office results in both lab work and referral to a specialist.

   Solution

   Let:

   L = event that a visit results in lab work

   S = event a visit results in referral to a specialist

   Thus, we’re interested in \(P(L \cap S)\)

   But what do we have?

   From the question, \(P(L) = 0.35\), \(P(S) = 0.25\), and \(P(L^C \cap S^C) = 0.50\)

   From the addition rule, we know that \(P(L \cup S) = P(L) + P(S) − P(L \cap S)\)

   Thus, \(P(L \cap S) = P(L) + P(S) – P(L \cup S)\)

   But we also know that \(P(L \cup S) = 1 – P(L \cup S)^C\)

   Thus, \(P(L \cap S) = P(L) + P(S) – (1 – P(L \cup S)^C) = P(L) + P(S) – 1 + P(L \cup S)^C\)

   Also, recall that \(P(L \cup S)^C = P(L^C \cap S^C)\)

   Thus, \(P(L) + P(S) – 1 + P(L \cup S)^C = P(L) + P(S) – 1 + P(L^C \cap S^C)\)

   $$ P(L \cap S) = 0.35 + 0.25 – 1 + 0.50 = 0.10 $$

   1.2 The Addition Rule for Mutually Exclusive Events

   Mutually exclusive is a term that describes two or more events that cannot occur at the same time. In most cases, it signifies a situation where one outcome supersedes another. The rolling of dice is a basic example. It is not possible to roll both a four and a six at the same time. Likewise, getting a four on the initial roll has no influence on whether or not a subsequent roll will produce a six. All throws of a die are independent.

   When two events, A and B, are mutually exclusive, the Addition Rule tells us that the probability that A or B will occur is the sum of the probability that either event will happen.

   $$ P(A \cup B) = P(A) + P(B) $$

   Example 1.2.1

   There are four equal sections in a spinner, each colored yellow, blue, orange, and black. How likely is it that the spinner will land on yellow or blue after a single spin?

   Let:

   Y = event that the spinner lands on yellow

   B = event that the spinner lands on red

   \(P(Y) =\frac {1}{4}\)

   \(P(B) = \frac {1}{4} \)

   All four sections cannot occur simultaneously, and therefore,

   $$ P(A \cup B) = P(A) + P(B) = \frac {1}{4} + \frac {1}{4} = \frac {1}{2} $$

   Example 1.2.2

   From a deck of 52 playing cards, what is the probability of drawing either a jack or a queen?

   Let J represent the event that a jack is drawn and B represent the event that a queen is drawn.

   $$ P(J \cup B) = P(J) + P(B) = \frac {4}{52} + \frac {4}{52} = \frac {8}{52} $$

2. Multiplication Rule

   The multiplication rule in probability allows us to calculate the probability of multiple events occurring together as long as we know the probabilities of those events individually. There are two versions for the multiplication rule: The general multiplication rule and the specific multiplication rule.

   2.1 The General Multiplication rule

   The general multiplication rule applies for events that are dependent (not independent). According to the rule, the probability that both events A and B will occur simultaneously is equal to the product of the probability of B occurring and the conditional probability that event A will occur given that B occurs.

   $$ P(A \cap B) = P(B) . P(A|B) $$

   Example 2.1.1

   Imagine you are interested in the probability of drawing queens in two consecutive draws, without replacement. Initially, the deck contains 4 queens out of 52 cards, thus the probability of a queen on the first draw is 4/52. Once you draw a queen (event Q1), the probability of drawing yet another queen changes. The new “dependent” probability of drawing that second queen (event Q2) is now 3/51.

   In notation form:

   $$ \begin{align*} P(Q1 \cap Q2) & = P(Q1) . P(Q2|Q1) \\ & = \frac {4}{52} . \frac {3}{51} = 0.4525\% \end{align*} $$

   2.2 The Specific Multiplication rule

   The specific multiplication rule of probability applies for events that are independent. According to the rule, the probability that both events A and B will occur simultaneously is equal to the product of their individual probabilities.

   $$ P(A \cap B) = P(A) . P(B) $$

   Example 2.2.1

   How likely is it that you will get “tails” twice in a row when you flip a fair coin? To put it differently, what is the probability of getting tails on the first flip and tails on the second flip?

   The probability of getting two “tails” in a row would be:

   $$ P(T \cap T) = \frac {1}{2} \times \frac {1}{2} = \frac {1}{4} $$

Learning Outcome

1.b Topic: General Probability – Calculate probabilities using the addition and multiplication rules.