Immunization

AnalystPrep’s Actuarial Exams Preparation Materials

For our question bank, study notes, quizzes, and all our video lessons: https://analystprep.com/shop/learn-practice-package-for-soa-exam-fm/

After completing this chapter, the candidate will be able to:

1. Define and recognize the definitions of the following terms:cashflow matching,immunization (including full immunization),Redington immunization.
2. Construct an investment portfolio to:
   • Redington immunize a set of liability cash flows.
   • Fully immunize a set of liability cashflows
   • Exactly match a set of liability cash flows.

Exact Matching (Dedication)

Suppose that an organization, at a valuation interest \(i\), has a present value of liabilities \(P_L\left(i\right)\) and the present value of the assets \(P_A\left(i\right)\). If it were possible to select a portfolio of assets that generates cash flows that exactly match the liabilities of the fund in terms of timing and amount, then the fund would be completely insulated against fluctuations of the interest rates. This is called an exact matching or dedication. Exact matching is just a theoretical concept, and in most cases, not achievable.

Example: Exact Matching (Dedication)

A company has a 95,030 liability due in one year and another 297,330 liability due in two years. The company has the following two types of bonds they can use to match these liabilities exactly:

• Bond A is a two-year 1000 par value bond with 6% annual coupons.
• Bond B is a one-year zero-coupon bond redeemable at 1000.

Determine the number of each type of bond the company should buy in order to exactly match the liabilities.

Solution

Let n be the number of bonds of type Bond A purchased.

Let m be the number of bonds of type Bond B purchased.

Consider the following timeline:

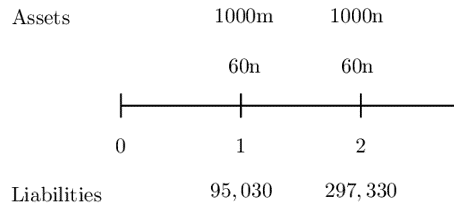
From the timeline,

• Bond A: two-year 1000 par value with 6% annual coupons (n of these).
• Bond B: one-year zero-coupon bond redeemable at 1000 (m of these).

Therefore the equations of values are given by:

$$ \begin{align*} 1000m+60n&=95,030\ldots\ldots\ldots(i) \\ 1060n&=297,330\ldots\ldots\ldots(ii) \end{align*} $$

Substituting Eq (ii) in Eq (i) we have:

$$ n=280.5\quad \& \quad m=78.2 $$

Immunization

It is possible to choose an asset portfolio that offers considerable protection against small changes in the interest rates. Now, define the net present value function as:

$$ P\left(i\right)=P_A\left(i\right)-P_L\left(i\right) $$

The idea behind the immunization is that, given a specific interest rate, \(i=i_0\), if possible, we have assets and liabilities arranged so that the graph of \(y=P(i)\) has a minimum of 0 located at \(i=i_0\).

In simple terms, immunization is the process of selecting asset portfolios that will protect the net present value function against small interest rate fluctuations.

Conditions Required for Immunizations

Condition 1

The first condition requires that the net present value function is equal to zero. That is:

$$ P\left(i\right)=P_A\left(i\right)-P_L\left(i\right)=0 $$

It, therefore, implies that:

$$ P_A\left(i\right)=P_L\left(i\right) $$

Condition 2:

The second condition requires that the first derivative of the net present value function be equal to 0. That is:

$$ P^{\prime}\left(i_0\right)=0 $$

From the first condition, it is easy to see that:

$$ P_A^{\prime}\left(i_0\right)=P_L^{\prime}\left(i_0\right) $$

Recall that we defined a modified duration as:

$$ ModD=\frac{-P^{\prime}(i)}{P(i)} $$

Using the first and the second conditions, we have the that:

$$ {ModD}_A\left(i_0\right)={ModD}_L\left(i_0\right) $$

Note that this is also true for Macaulay duration:

$$ {MacD}_A\left(i_0\right)={MacD}_L\left(i_0\right) $$

Condition 3

In order to make sure that the net present value function has a minimum of 0 located at \(i=i_0\), then the second derivative of the net present value function should be positive so that the graph is concave up. That is:

$$ P^{\prime\prime}\left(i_0\right)>0 $$

Now we know that:

$$ P\left(i\right)=P_A\left(i\right)-P_L\left(i\right) $$

Since the derivative is a linear operator, we have that:

$$ \begin{align*} P^{\prime\prime}\left(i_0\right)&=P_A^{\prime\prime}i-P_L^{\prime\prime}i>0 \\ \Rightarrow& P_A^{\prime\prime}\left(i_0\right)> P_L^{\prime\prime}\left(i_0\right) \end{align*} $$

Recall that modified convexity is defined as:

$$ ModC=\frac{P^{\prime\prime}(i)}{P(i)} $$

Now using condition 1 and condition 3, it is easy to see that:

$$ {ModC}_A\left(i_0\right)>{ModC}_L\left(i_0\right) $$

Note that this is also true for the Macaulay convexity. That is:

$$ {MacC}_A\left(i_0\right)>{MacC}_L\left(i_0\right) $$

The conditions discussed above are called the Redington’s Immunization, named after a British actuary Frank Redington. Briefly, Redington’s condition can be stated as:

1. The present value of the assets equals the present value of the liabilities. That is, $$ P_A\left(i\right)=P_L\left(i\right) $$
2. The duration of the assets equals the duration of the liabilities.

   $$ {ModD}_A\left(i_0\right)={ModD}_L\left(i_0\right) $$

   And

   $$ {MacD}_A\left(i_0\right)={MacD}_L\left(i_0\right) $$

3. The convexity of the assets is greater than the convexity of the liabilities. That is:

   $$ {ModC}_A\left(i_0\right)>{ModC}_L\left(i_0\right) $$

   And

   $$ {MacC}_A\left(i_0\right)>{MacC}_L\left(i_0\right) $$

Example: Redington Immunization Conditions

A company has to pay $2000 at the end of 2 years and $4000 after 4 years. The present annual effective rate of interest is 10%. The company wishes to immunize the interest rate risk by investing in zero-coupon bonds. A risk manager advises the company to buy the following zero-coupon bonds:

• One-year zero-coupon bond with a face value of $44.74
• Three-year zero-coupon bond with a face value of $2450.83
• Five-year zero-coupon bond with a face value of $500

Ascertain that if or not, the portfolio is immunized according to Redington’s conditions.

Solution

The first condition is:

$$ P_A\left(i\right)=P_L\left(i\right) $$

Now,

$$ P_A\left(i\right)=44.74\left(1.1\right)^{-1}+2450.8\left(1.1\right)^{-3}+500\left(1.1\right)^{-5}=2192.46 $$

And

$$ \begin{align*} P_L\left(i\right)&=1000\left(1.1\right)^{-2}+2000\left(1.1\right)^{-4}=2,192.47 \\ \Rightarrow V\left(i\right)_A&\approx\ V\left(i\right)_{L\ \ } \end{align*} $$

The second condition is:

$$ {MacD}_A\left(i_0\right)={MacD}_L\left(i_0\right) $$

Recall that the Macaulay duration is given by:

$$ MacD=\frac{\sum{{t\cdot C}_tv^t}}{\sum{C_t\cdot v^t}} $$

Now,

$$ { MacD }_{ A }\left( i_{ 0 } \right) =\frac { \left[ 1\times 44.74\left( 1.1 \right) ^{ -1 }+3\times 2450.83\left( 1.1 \right) ^{ -3 }+5\times 500\left( 1.1 \right) ^{ -5 } \right] }{ 2192.47 } =3.2461 \text{ years}. \\ Τ\left(i\right)_B=\cfrac{\left[2\times1000\left(1.1\right)^{-2}+4\times2000\left(1.1\right)^{-4}\right]}{2192.47}=3.2461 \text{ years} $$

So,

$$ {MacD}_A\left(i_0\right)={MacD}_L\left(i_0\right) $$

For the third condition, we will use modified convexity so that we will be proving that:

$$ {ModC}_A\left(i_0\right)>{ModC}_L\left(i_0\right) $$

We know that:

$$ ModC=\frac{P^{\prime\prime}(i)}{P(i)} $$

Now,

$$ \begin{align*} {ModC}_A\left(i_0\right)\\ &=\frac{2\times1\times44.74\left(1.1\right)^{-1}+4\times3\times2450.83\left(1.1\right)^{-3}+6\times5\times500\left(1.1\right)^{-5}}{{1.1}^2\times2192.47} \\ &=11.87 \end{align*} $$

And

$$ \begin{align*} {ModC}_B\left(i_0\right)&=\frac{3\times2\times1000\left(1.1\right)^{-2}+5\times4\times2000\left(1. mommabe.com 1\right)^{-4}}{{1.1}^2\times2192.47} \\ &=12.17 \end{align*} $$

$$ {\Rightarrow} {ModC}_A\left(i_0\right)>{ModC}_L\left(i_0\right) $$

Since all the Redington’s have been satisfied, the assets are immunized against small changes in the valuation rate of interest.

As shown by the example above, it is possible to construct a portfolio of assets such that the Net present value function (net-worth of a financial institution) is guaranteed to be positive at any interest rate position.

Example: Immunization

A company has a liability of 72,900 due in two years. They wish to immunize this liability at an interest rate that corresponds to an annual discount factor of v=0.9 by using a one-year zero-coupon bond and a three-year zero-coupon bond.

Determine how much of the one and three-year bonds should be bought.

Solution

Let \(F_1\) denote the face amount of the 1-year bond, and

Let \(F_3\) denote the face amount of the 3-year bond.

Consider the following timeline:

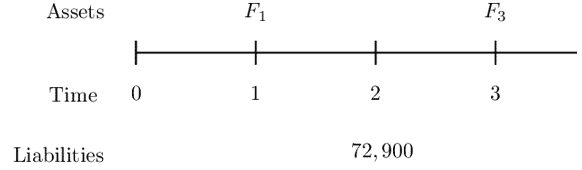
Recall that the following conditions for immunization:

Condition 1:

The present value of the assets equals the present value of the liabilities.

$$ \Rightarrow\ F_1v^1+F_3v^3=72,900v^2\ldots\ldots\ldots(i) $$

Condition 2:

The duration of the assets equals the duration of the liabilities. From the question, we have that:

$$ {MacD}_A=\frac{F_1v^1+3F_3v^3}{F_1v^1+F_3v^3}=\frac{F_1v^1+3F_3v^3}{72,900v^2} $$

And

$$ {MacD}_L=\frac{2\cdot72,900v^2}{72,900v^2} $$

We know that:

$$ {MacD}_A\left(i_0\right)={MacD}_L\left(i_0\right) \\ \Rightarrow\ F_1v^1+3F_3v^3=2\cdot72,900v^2\ldots\ldots\ldots\ldots(ii)$$

Solving Eq (i) and Eq (ii), we have:

$$ \cfrac { \left\{ \begin{matrix} -\left( { F }_{ 1 }{ V }^{ 1 }+{ F }_{ 3 }{ V }^{ 3 }=72,900{ V }^{ 2 } \right) \\ { F }_{ 1 }{ V }^{ 1 }+3{ F }_{ 3 }{ V }^{ 3 }=2\cdot 72,900v^{ 2 } \end{matrix} \right\} } { \Rightarrow {F_3}v^3=72,900v^2 } \\ \therefore F_3=40,500 $$

Substituting \(F_3\) in Eq (i), we have:

$$ F_1=32,805 $$

Full Immunization

A full immunization position is said to be reached if, at any point where the interest rate changes, say from \(i\) to \(i\pm\epsilon_i\) where \(\epsilon_i\) is a small change in the interest rate, then:

$$ P\left(i\right)=P_A\left(i\right)-P_L\left(i\right)\geq0,\text{ for all } i>0 $$

In a more precise statement, full immunization at \(i=i_0\) would eliminate the risk of adverse effects created by all changes in interest rates.

Full immunization involves funding a liability using a portfolio of assets that generates cash inflows to counter the negative effects of the liabilities.

Using similar notations as above, the conditions for full immunization can be stated as:

1. \(P_A\left(i\right)=P_L\left(i\right).\) That is, the present value of the assets is exactly equal to the present value of the liabilities.
2. \({ModD}_A\left(i_0\right)={ModD}_L\left(i_0\right)\) and \({MacD}_A\left(i_0\right)={Mac}_L\left(i_0\right)\).That is, the duration of the assets and the liabilities are exactly equal.

Looking at the example above, the conditions for full immunization has been satisfied.

Limitations of Immunization

Immunization might look so promising while coming up with strategies to curb the backward movement of businesses, but it has a tone of limitations.

• The method of immunization requires a continuous rebalancing of portfolios to keep the asset-liability ratio equal to one.
• The assets’ and liabilities’ cash flows are, most of the time, approximate values since there exist many uncertainties.
• The theory of the immunization is based on the small changes in the interest rate and says nothing about large changes.
• Immunization assumes a flat yield curve and also requires that the interest rate changes be the same at all times, which in many cases, is very rare.
• The theory eliminates the probability of making a large profit.

Despite the limitations, immunization remains to be an important theory in choosing assets. As a matter of knowing, the best alternative for immunization is called asset-liability modeling.