Valuation of an Interest Rate Option

Interest rate options are options with an interest rate as the underlying. A call option on interest rates has a positive payoff when the current spot rate is greater than the exercise rate.

$$ \begin{align*} \text{Call option payoff} & =\text{Notional amount }\times \\ & [\text{max } (\text{Current spot rate} – \text{Exercise rate},0)] \end{align*} $$

On the other hand, a put option on interest rates has a positive payoff when the current spot rate is less than the exercise rate.

$$ \text{Put payoff} =\text{Notional amount} \times [\text{max } (\text{Exercise rate} – \text{Current spot rate},0)] $$

We can apply the binomial model to value such interest rate options.

Example: Calculating the Value of an Interest Rate European Option

Consider a two-year European-style call option with a one-year spot rate compounded annually as the underlying. The exercise rate is 6%. The two-period interest rate tree is given below:

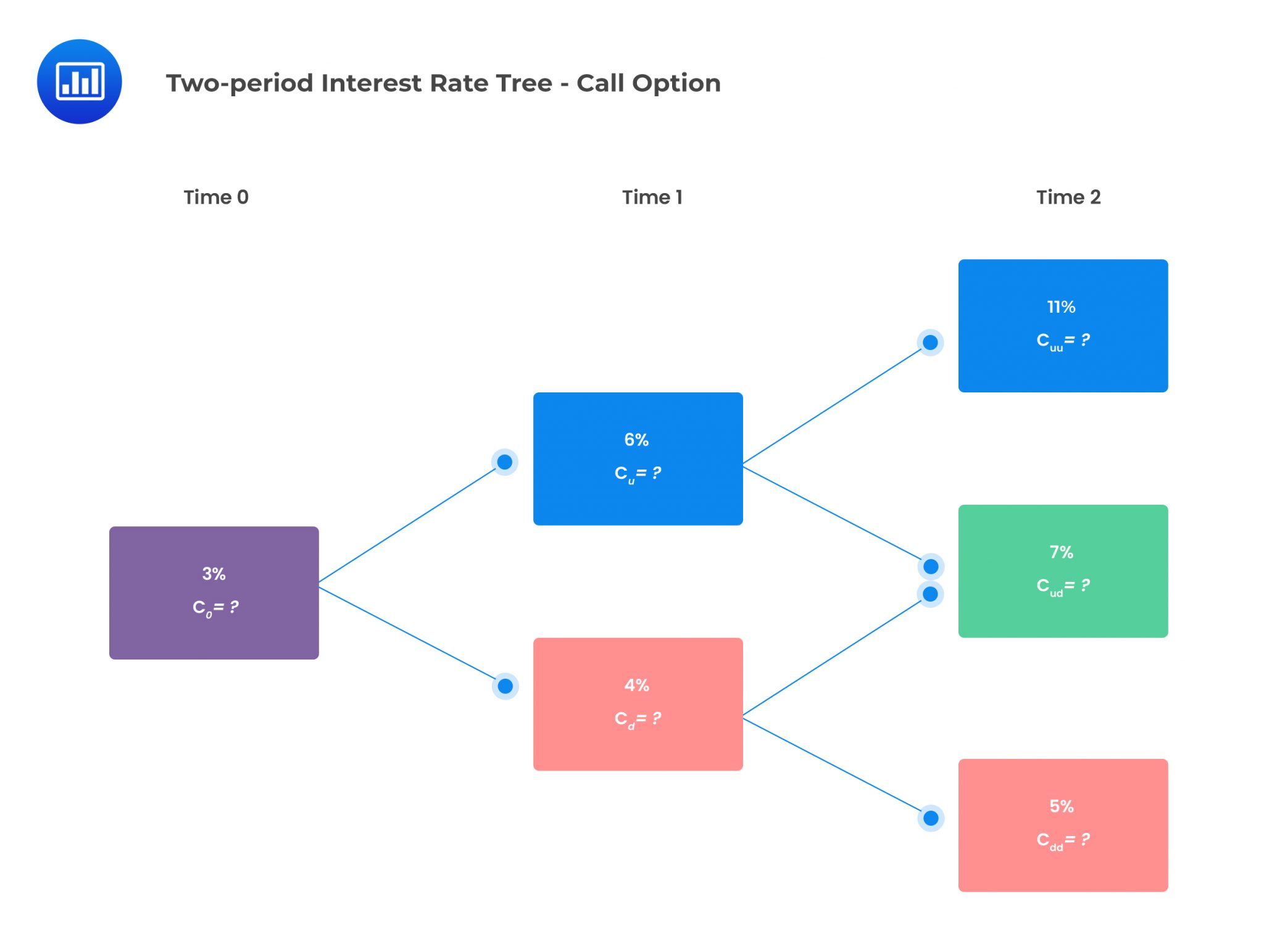Assume that the notional principal of each option is $500,000, and the risk-neutral probability of an up jump is 0.5. The value of the European call option can be determined as follows:

Payoffs at Time 2

$$ \begin{align*} c_{uu} &=max(0, S_0u^2-K) \\ c_{uu} &=max(0,0.11-0.06)=0.05 \\ C_{ud} &=Max\left(0,S_0ud-K\right) \\ C_{ud} &=max{\left(0,0.07-0.06\right)}=0.01 \\ c_{dd} &=Max(0,S_0d^2-K) \\ c_{dd} &=max{\left(0,0.05-0.06\right)}=0 \end{align*} $$

Value of Call at Time 1

$$ \begin{align*} c_u & =PV_{1,2}\left[qc_{uu}\ +\left(1 – q\right)c_{ud}\right] \\ c_u &=\frac{1}{1.06}\left[0.5\times0.05+\left(1-0.5\right)\times0.01\right]=0.028302 \\ c_d & =PV_{1,2}\left[qc_{ud} +\left(1 – q\right)c_{dd}\right] \\ c_d &=\frac{1}{1.04}[0.5\times0.01+\left(1-0.5\right)\times0)]=0.004808 \end{align*} $$

Value of Call at Time 0

$$ \begin{align*} c_0 & =PV_{0,1}\left[qc_u +\left(1 – q\right)c_d\right] \\ c_0 &=\frac{1}{1.03} \left[0.5\times0.028302+\left(1-0.5\right)\times0.004808 \right]=0.01607 \end{align*} $$

The call value at time 0 is then obtained by multiplying with the notional amount:

$$ \text{Call value} =0.01607\times$500,000=$8,035 $$

Question

Consider a two-year European-style put option with the annually compounded one-year spot interest rate as the underlying. The exercise rate is 6%. The two-period interest rate tree is given below:

Assume that the notional principal of each option is $500,000, and the risk-neutral (RN) probability of an up jump is 0.5. The value of the European put option is closest to:

1. $1,167.
2. $5,835.
3. $8,035.

Solution

The correct answer is A.

Put Payoffs at time 2

Similar to a call option, a put option will have three possible payoffs:

$$ \begin{align*} p_{uu}& = Max(0,K – S_0u^2) \\ p_{uu} & = Max(0,0.06 – 0.11)=0 \\ p_{ud} & = Max(0,K – S_0ud) \\ p_{ud} & = Max(0,0.06 – 0.07)=0 \\ p_{dd} & =Max(0,K – S_0dd) \\ p_{dd} & = Max(0,0.06 – 0.05)=0.01 \end{align*} $$

Value of Put at Time 1

$$ \begin{align*} p_u & =PV_{1,2}\left[qp_{uu} +\left(1 – q\right)p_{ud}\right] \\ p_u &=\frac{1}{1.06}\left[0.5\times0+\left(1-0.5\right)\times0\right]=0 \\ p_d & =PV_{1,2}\left[qp_{ud} +\left(1 – q\right)c_{dd}\right] \\ c_d &=\frac{1}{1.04} \left[0.5\times0+\left(1-0.5\right)\times0.01) \right]=0.004808 \end{align*} $$

Value of Put at Time 0

$$ \begin{align*} p_o & =PV_{0,1}\left[qp_u +\left(1- q\right)p_d\right] \\ c_0 &=\frac{1}{1.03} \left[0.5\times0+\left(1-0.5\right)\times0.004808 \right]=0.00233398 \end{align*} $$

The put value at time 0 is then obtained by multiplying by the notional amount:

$$ \text{put value} =0.002334\times$500,000=$1,167 $$

Reading 34: Valuation of Contingent Claims

LOS 34 (d) Calculate and interpret the value of an interest rate option using a two-period binomial model.