Updating Probability Using Bayes’ Fo ...
Bayes’ formula is used to calculate an updated or posterior probability given a... Read More
Covariance is a measure of how two variables move together. The sample covariance of X and Y is calculated as follows:
$${s}_{XY}=\frac{\sum_{i=1}^{N}\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{n-1}$$
The formula above implies that the sample covariance is the mean of the product of the deviations in the two random variables and from their sample means.
If the covariance between two random variables is positive, it means they move in the same direction. When one is below its mean, the other is also below its mean, and vice versa.
A major drawback of covariance is that it is difficult to interpret since its value can vary from negative infinity to positive infinity.
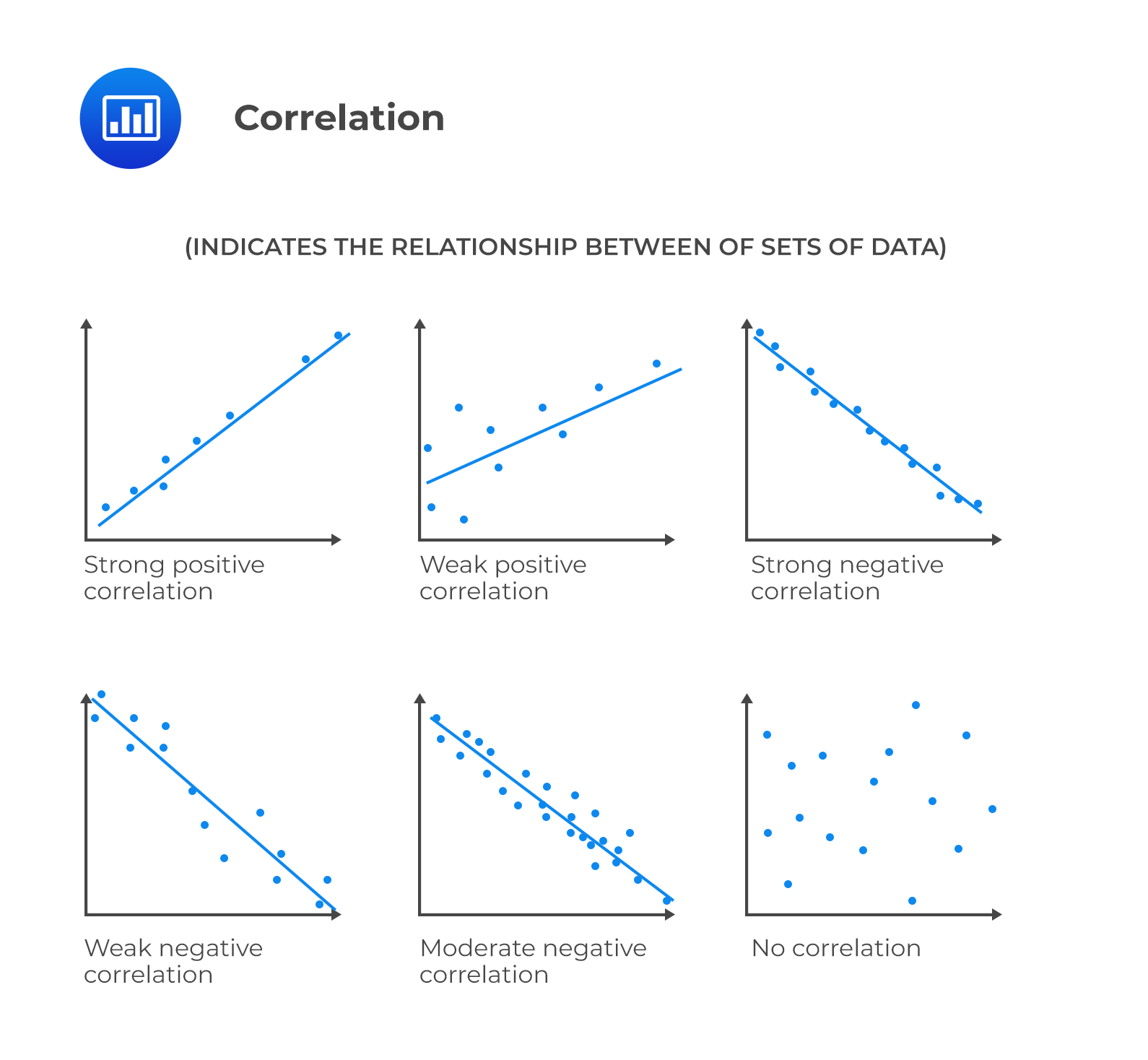
Correlation is a standardized measure of the linear relationship between two variables. It takes the covariance and divides it by the product of the standard deviations of both variables. As a result, its value ranges between -1 and +1 and is easier to interpret.
The sample correlation coefficient is calculated as follows:
$$r_{xy}=\frac{s_{XY}}{s_X\times s_Y}$$
Where:
\(s_{X Y}\) = Covariance between variable X and Y.
\(s_{X}\) = Standard deviation of variable X.
\(s_{Y}\) = Standard deviation of variable Y.
Question
The correlation coefficient between X and Y is 0.7, and the covariance is 29. If the variance of Y is 25, the variance of X is closest to:
- 8.29.
- 29.00
- 68.65.
Solution
The correct answer is C.
$$\begin{align} r_{X Y} &=\frac{s_{X Y}}{s_{X} \times s_{Y}}\\ \Rightarrow 0.7 &=\frac{29}{s_{X} \times 5} \\ \therefore s_{X}&=8.2857\\ \\ \text{Variance} &=8.2857^2=68.65 \end{align}$$