Bernoulli Random Variables and Binomial Random Variables

Probability distributions have different shapes and characteristics. As such, we describe a random variable based on the shape of the underlying distribution.

A Bernoulli Random Variable

A Bernoulli trial is an experiment that has only two outcomes: success (S) or failure (F). You should note that we use the words “success” and “failure” just for labeling purposes, and therefore these words may not necessarily carry with them the ordinary meanings.

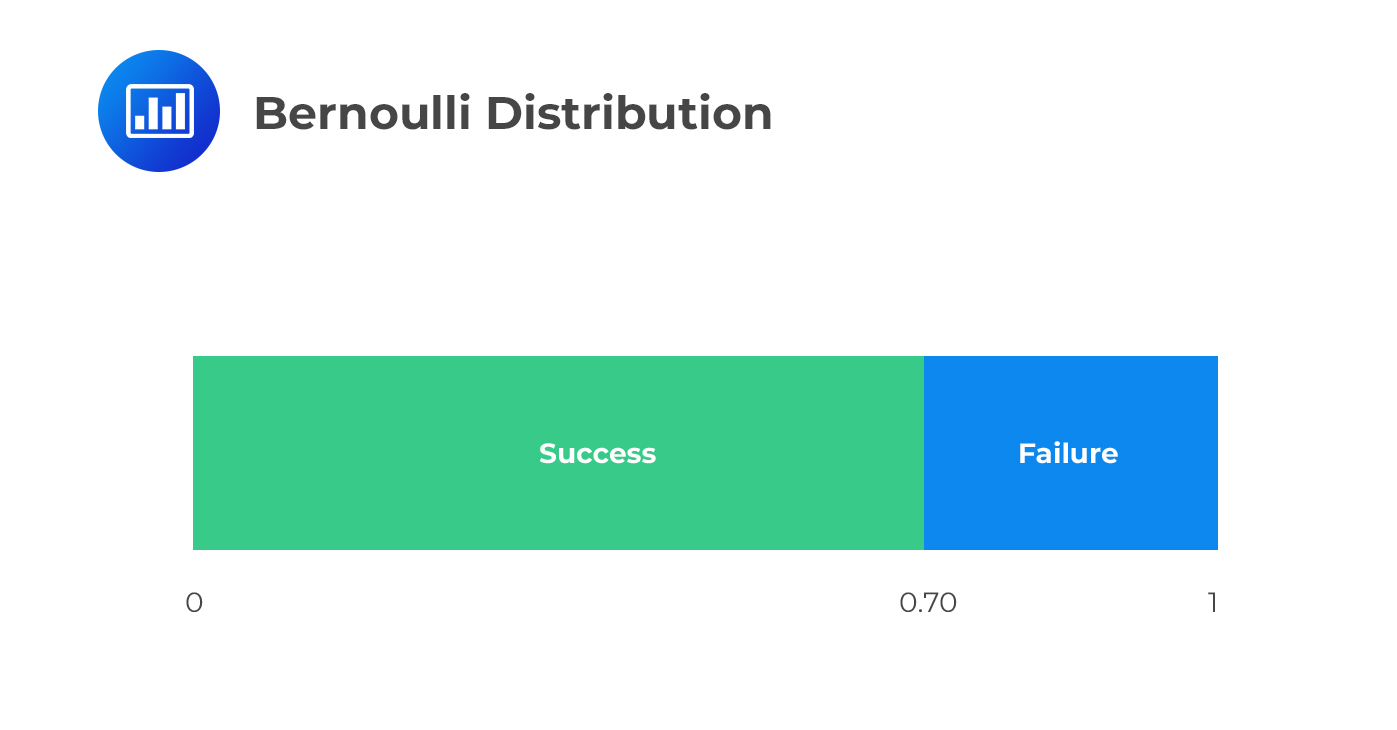
We define the random variable \(X\) by \(X(s) = 1\), with a probability of \(p\) and \(X(f) = 0\) with a probability of \(1-p\). As such, \(X\) is the number of successes that occur with a probability between 0 or 1. The probability function of Bernoulli random variables is given by:

$$
f(x)=\left\{\begin{array}{ll}
p^{x}(1-p)^{1-x} & \text { if } x=0,1 \\
0 & \text { elsewhere }
\end{array}=\left\{\begin{array}{cl}
p & \text { if } x=1 \\
1-p & \text { if } x=0
\end{array}\right.\right.
$$

A Bernoulli variable can sometimes be used as an “indicator” to indicate whether a given event occurs. We could set \(X = 1\) if event B occurs and \(X = 0\) if event B does not occur. For example, event B could be a return of over 10% on a stock.

A Binomial Random Variable

A binomial random variable is the number of successes in n Bernoulli trials where:

• The trials are independent: The outcome of any trial does not depend on the outcomes of the other trials.
• The trials are identical: All trials’ probability of success is equal.

For example, the tossing of a coin has two mutually exclusive outcomes, where the probability of the outcome of any toss (trial) is not affected by prior outcomes from prior trials.

The Binomial Distribution

The binomial distribution is a sequence of \(n\) Bernoulli trials where the outcome for every trial can be a success or a failure.

Suppose the probability of success is \(p\):

$$ P\left( X=x \right) =\left( \begin{matrix} n \\ x \end{matrix} \right) { p}^{ x }\left( 1-p \right) ^{ n-x },x=0,1,2,…,n;0<p<1 $$

Where:

$$ \left( \begin{matrix} n \\ x \end{matrix} \right) ={ \quad }^{ n }{ C }_{ x }=\frac { n! }{ \left( n-x \right) !x! } $$

$$ \text{Mean of X} = n p $$

$$ \text{Variance of X} = n p (1 – p )$$

Note to candidates: Sometimes, the probability of success can be denoted by \(p\), and \((1-p)\) will denote the probability of failure.

Example: Binomial Distribution

The probability of surviving an attack by a certain disease is 60%. What is the probability that at least 11 out of a group of 12 people affected by the disease will survive?

Solution

The number of survivors is distributed binomially with parameters \(n = 12\) and \(θ = 0.6\):

$$ \begin{align*} P(X \ge 11) & = P(X = 11 \text{ or } 12) \\ &={ ^{ 12 }{ C }_{ 11 }{ \times 0.6 }^{ 11 }\times { 0.4 }^{ 1 }+^{ 12 }{ C }_{ 12 }{ \times 0.6 }^{ 12 } } \\ &= \cfrac {12!}{(1!11!)} 0.6^{11} \times 0.4^1 + \cfrac {12!}{(0!12!)} \times 0.6^{12} \\ &= 12 \times  0.003628 \times  0.4 + 0.6^{12} \\ &= 0.01959 \end{align*} $$

Note to candidates: The binomial distribution is symmetric when the probability of success on a trial is 0.50. When the probability of success is not equal to 0.50, the binomial distribution is non-symmetrical or skewed.

Question

A bowl contains blue and orange balls. The probability of drawing a blue ball in any attempt is 0.5. Suppose you draw 5 balls from the bag, what is the probability that 3 of the 5 balls drawn are blue?

1. 3.125%.
2. 25%.
3. 31.25%.

Solution

The correct answer is C.

$$\begin{align}P(X = 3) &={5\choose 3} \times 0.5^3 \times 0.5^2\\&= 10 \times 0.03125\\&= 0.3125\end{align}$$