Understanding a Parameter, a Statistic ...
[vsw id=”alD9eAT2lQU” source=”youtube” width=”611″ height=”344″ autoplay=”no”] A parameter refers to a measure that... Read More
A random variable is said to have the normal distribution (Gaussian curve) if its values make a smooth curve that assumes a “bell shape.” A normal variable has a mean “μ,” pronounced as “mu,” and a standard deviation “σ,” pronounced as “sigma.” All normal distributions have a distinguishable bell shape regardless of the mean, variance, and standard deviation.
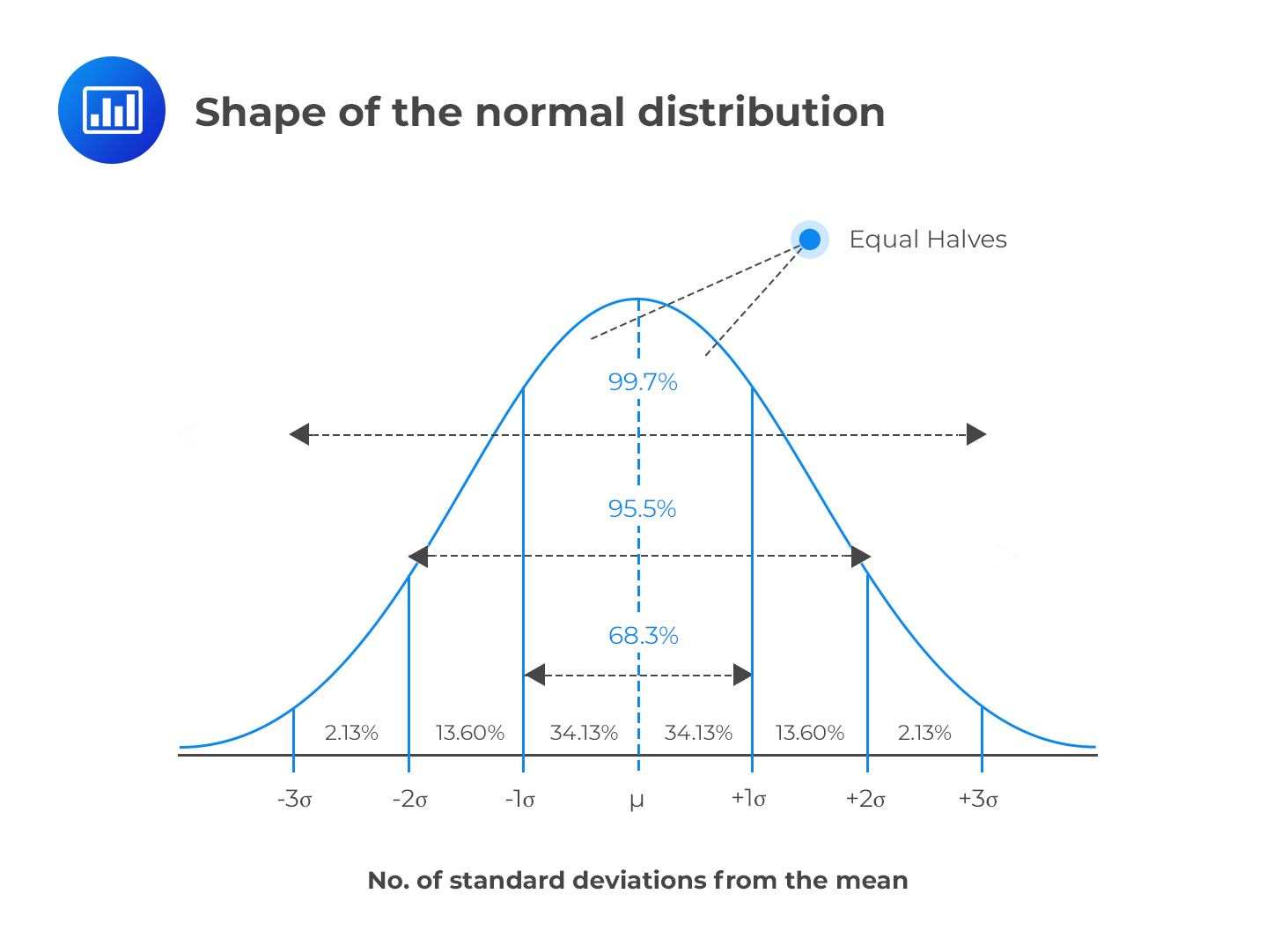
A normal distribution has certain properties that make it a useful tool in the world of finance.
To determine the probability that a random variable X lies between two points, ‘a’ and ‘b’:
$$ P\left( a < X < b \right) =\int _{ a }^{ b }{ f\left( x \right)dx } $$
The normal distribution is very important in statistical analysis, especially because of the central limit theorem. The theorem asserts that any distribution becomes normally distributed when the number of variables is sufficiently large. For instance, the binomial distribution tends to “change” into the normal distribution with mean nθ and variance nθ(1 – θ).
Reading 9 LOS 9i:
Explain the key properties of the normal distribution.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.