Spot Rate vs. Forward Rates (Calculations for CFA® and FRM® Exams)

Understanding how to calculate forward rates from spot rates is a must for CFA and FRM candidates. This guide breaks down the forward rate formula step by step, showing you exactly how it appears on the exams. With simple examples and exam-focused explanations, you’ll quickly grasp how spot and forward rates interact—and why it matters in fixed income and derivatives.

Spot Rates

A spot interest rate gives you the price of a financial contract on the spot date. The spot date is the day when the funds involved in a business transaction are transferred between the parties involved. It could be two days after a trade, or even on the same day the deal is completed. A spot rate of 5% is the agreed-upon market price of the transaction based on current buyer and seller action.

Forward Rate Formulas – CFA & FRM Quick Guide

1. Forward Rate Formula (1-period):

f2,1=(1+S2)2(1+S1)−1f_{2,1} = \frac{(1 + S_2)^2}{(1 + S_1)} – 1f2,1​=(1+S1​)(1+S2​)2​−1

2. General Forward Rate Formula:

fn,m=((1+Sn)n(1+Sm)m)1n−m−1f_{n,m} = \left( \frac{(1 + S_n)^n}{(1 + S_m)^m} \right)^{\frac{1}{n – m}} – 1fn,m​=((1+Sm​)m(1+Sn​)n​)n−m1​−1

Where:

• fn,mf_{n,m}fn,m​: Forward rate from year $m$ to year $n$

• SnS_nSn​: Spot rate for maturity $n$

• SmS_mSm​: Spot rate for maturity $m$

• $n>m$

Calculating the Price of a Bond using Spot Rates

Formula

The general formula for calculating a bond’s price given a sequence of spot rates is given below:

\({ PV }_{ bond }=\frac { PMT }{ { (1+{ Z }_{ 1 }) }^{ 1 } } +\frac { PMT }{ { (1+{ Z }_{ 2 }) }^{ 2 } } +…+\frac { PMT+Principal }{ { (1+{ Z }_{ n }) }^{ n } } \)

Where:

\({ PV }_{ bond }\)  is the present value of the price of the bond;

PMT is the coupon payment per period;

\( { Z }_{ 1 },{ Z }_{ 2 }\) and \( { Z }_{ n }\) are the spot rates for periods 1,2 and n respectively; and

n is the number of evenly spaced periods to maturity.

Suppose that:

• The 1-year spot rate is 3%;
• The 2-year spot rate is 4%; and
• The 3-year spot rate is 5%.

The price of a 100-par value 3-year bond paying 6% annual coupon payment is 102.95.

$$
\begin{array}{l|cccccc}
\text{Time Period} & 1 & 2 & 3 \\
\hline
\text{Calculation} & \frac {\$6}{{\left(1+3\%\right)}^{ 1 } } & \frac { \$6 }{ { \left( 1+4\% \right) }^{ 2 } } & \frac { \$106 }{ { \left( 1+5\% \right) }^{ 3 } } \\
\hline
\text{Cash Flow} & \$5.83 & +\$5.55 & +\$91.57 & =\$102.95 \\
\end{array}
$$

Spot rates are also applied in determining the yield to maturity of a bond.

Calculating the Yield-to-maturity of a Bond using Spot Rates

Continuing on the same example, this 3-year bond is priced at a premium above par value, so its yield-to-maturity must be less than 6%. We can now use the financial calculator to find the yield-to-maturity using the following inputs:

• n = 3;
• PV = -102.95; (Since this is a cash outflow)
• PMT = 6; (Since this is a cash inflow for the investor)
• FV = 100; (Since this is a cash inflow for the investor)
• CPT => I/Y = 4.92 (Which signifies 4.92%)

The yield-to-maturity is found to be 4.92%, which we can confirm with the following calculation:

$$
\begin{array}{l|cccccc}
\text{Time Period} & 1 & 2 & 3 \\
\hline
\text{Calculation} & \frac {\$6}{{\left(1+4.92\%\right)}^{ 1 } } & \frac { \$6 }{ { \left( 1+4.92\% \right) }^{ 2 } } & \frac { \$106 }{ { \left( 1+4.92\% \right) }^{ 3 } } \\
\hline
\text{Cash Flow} & \$5.719 & +\$5.450 & +\$91.770 & =\$102.95 \\
\end{array}
$$

Forward Rates

In theory, forward rates are prices of financial transactions that are expected to take place at some future point.

A forward rate indicates the interest rate on a loan beginning at some time in the future, whereas a spot rate is the interest rate on a loan beginning immediately. Thus, the forward market rate is for future delivery after the usual settlement time in the cash market.

Deriving Forward Rates from a Set of Spot Rates

\({ Z }_{ n }\), the \(n\)-year spot rate, is a measure of the average interest rate over the period from now until \(n\) years’ time.

The forward rate, \({ f }_{ t,r }\), is a measure of the average interest rate between times \(t\) and \(t + r\). It’s the interest rate agreed today \((t=0)\) on an investment made at time \(t>0\) for a period of \(r\) years.

The one-year forward rate, \({ f }_{ t,1 }\), is therefore the rate of interest from time \(t\) to time \(t +1\). It can be expressed in terms of spot rates as follows:

$$ 1+{ f }_{ t,1 } = \frac{{{(1+{Z}_{t+1})}}^{t+1}}{{(1+{Z}_{t})}^{t}} $$

Alternatively,

Step 1: Use the formula:

$$ 1+{ f }_{ t,1 }=\frac {V_2}{V_1} $$

Where \(V_1\) is the value to which a dollar grows by time \(T_1\) and \(V_2\) is the value to which a dollar grows by \(T_1\).

Step 2: Calculate the interest rate that equates the value of one dollar at time \(T_1\) to the value of one dollar at time \(T_2\).

Example: Calculating the one-year forward rate.

You are given the following spot rates:

• 1-year spot rate: 5%;
• 2-year spot rate: 6%.

Determine the one-year forward rate one year from today, i.e., \(f_{1,1}\).

There are 2 ways to solve this question:

1. Using the Formula

$$ 1+{ f }_{ t,1 } = \frac{{{(1+{Z}_{t+1})}}^{t+1}}{{(1+{Z}_{t})}^{t}} $$

$$ (1 + \text{1-year spot}) × (1 + \text{1-year forward rate at time 1}) = (1 + \text{2-year spot})^2 $$

$$ (1.05)\ × (1\ +\ f_{1,1}) = {(1.06)}^2 $$

$$  (f_{1,1}) = 7.0095%$$

2. Using the Timeline

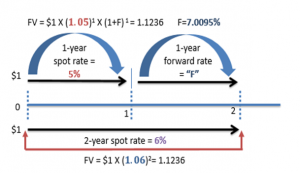
We use the principle of no-arbitrage. The golden rule to remember while using the timeline is that no matter which route you take to “time travel” from one period to the other- the end result (Future Value) will always be the same.

There are 2 possible routes we could take here

1. Invest for one year at the spot rate of 5% and then invest for another year at the unknown forward rate “F.”
2. Invest for two years at the spot rate of 6%.

As per the assumption of no-arbitrage, we should arrive at the same value for both.

By equating i & ii, we get F = 7%, which is the same as what we got using the formula.

https://analystprep.com/shop/frm-part-1-and-part-2-complete-course-by-analystprep/