Demystifying Forward Rate Agreements (Calculations for CFA® and FRM® Exams)

A forward rate agreement (FRA) is a cash-settled over-the-counter (OTC) contract between two counterparties, where the buyer is borrowing (and the seller is lending) a notional sum at a fixed interest rate (the FRA rate) and for a specified period starting at an agreed date in the future.

The purpose of FRA is to lock in borrowing or a lending rate for some time in the future. Typically, it involves two parties exchanging a fixed interest rate for a floating rate.

An FRA involves Two Counterparties:

• The borrower: The long pays a fixed rate and receives floating rates. Think of “buying money.” If LIBOR rises, the long will gain.
• The lender: The short pays a floating rate and receives a fixed rate. Think of “selling money.” If LIBOR falls, the short will gain.

The FRA buyer enters into the contract to protect itself from a future increase in interest rates; the seller of the FRA wants to protect itself from a future decline in interest rates.

FRM Part 1 and Part 2 Complete Online Course

Naming Convention (FRM Exam)

FRAs are denoted in the form of “X × Y,” where X and Y are months. So, a 1 × 4 FRA is called “1 by 4”.

Implying that:

A 1 × 4 FRA expires in 30 days (one month), and the theoretical loan is for a time period of the difference between 1 and 4 (three months = 90 days). That is, a three-month Libor determines the FRA’s payoff, but the FRA expires in one month.

Example 1: Understanding FRAs 

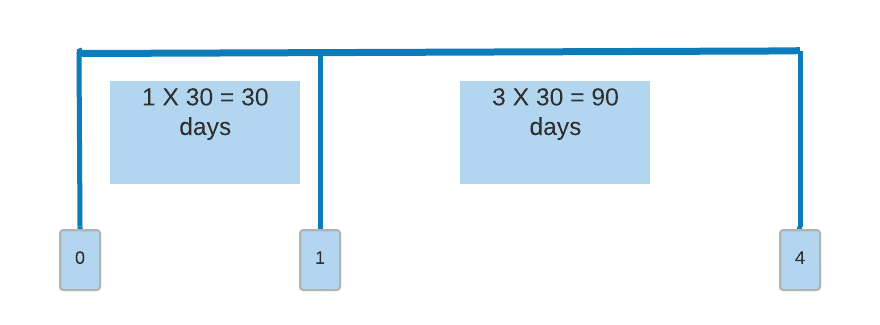
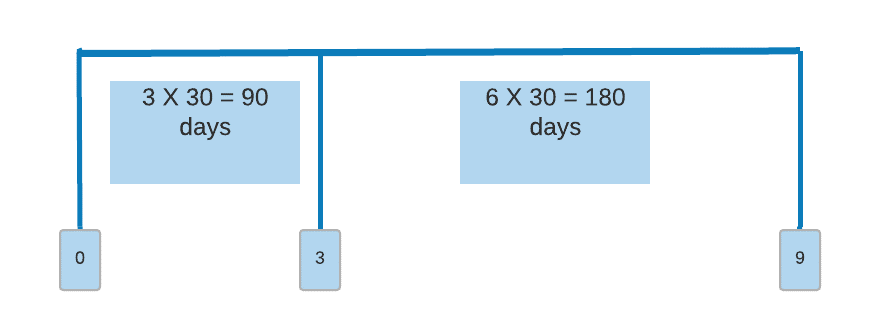
A 3 × 9 FRA refers to:

1. A 90-day LIBOR loan starting 270 days from now.
2. 270-day LIBOR loan starting 90 days from now.
3. 180-day LIBOR loan starting 90 days from now.
4. 270-day LIBOR loan starting 180 days from now.

Solution

The correct answer is C.

3-by-9 means a 180-day LIBOR loan starting 90 days from now.

FRA vs. Forwards

The forward rate specified in the FRA is compared with the current LIBOR rate, where:

• • If the current LIBOR is greater than the FRA rate, the long can effectively borrow at a below-market rate. The long receives a payment based on the difference between the two rates.
  • However, if the current LIBOR was lower than the FRA rate, then long makes a payment to the short. The payment ends up compensating for any change in interest rates since the contract date

Illustration

Example 2: FRA Valuation

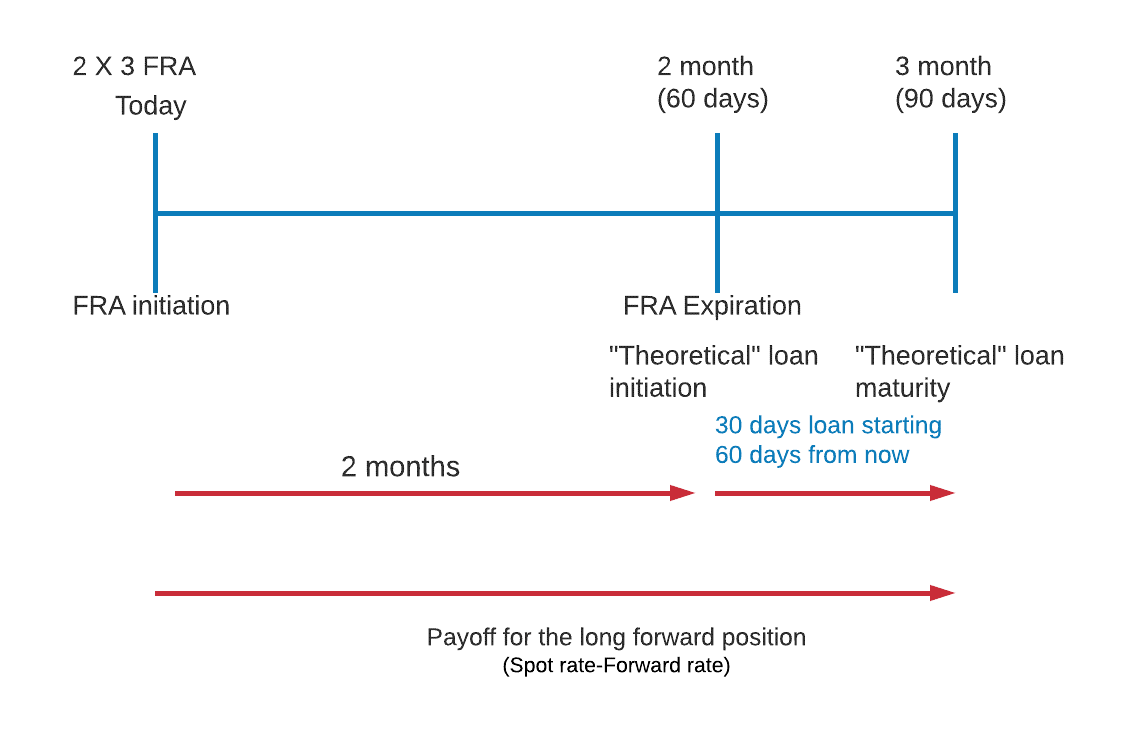
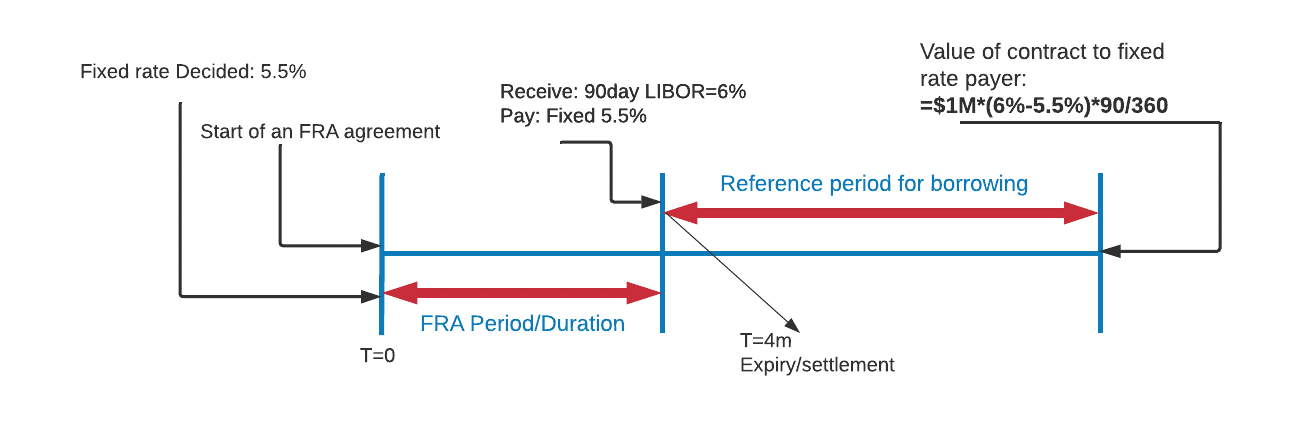
Suppose we have a 1 x 4 FRA with a notional principal of $1 million. At contract expiration, the 90-day LIBOR at settlement is 6% and the contract rate is 5.5%.

The value of the FRA at maturity is closest to:

Solution

$$ \begin{aligned} &\begin{array}{c} \text{Payment} \\ \text{to the Long} \end{array} = \text{Notional principal} \times \frac{(\text{Rate at settlement} – \text{FRA rate}) \times \frac{\text{Days}}{360}}{1 + \text{Rate at settlement} \times \frac{\text{Days}}{360}} \end{aligned} $$

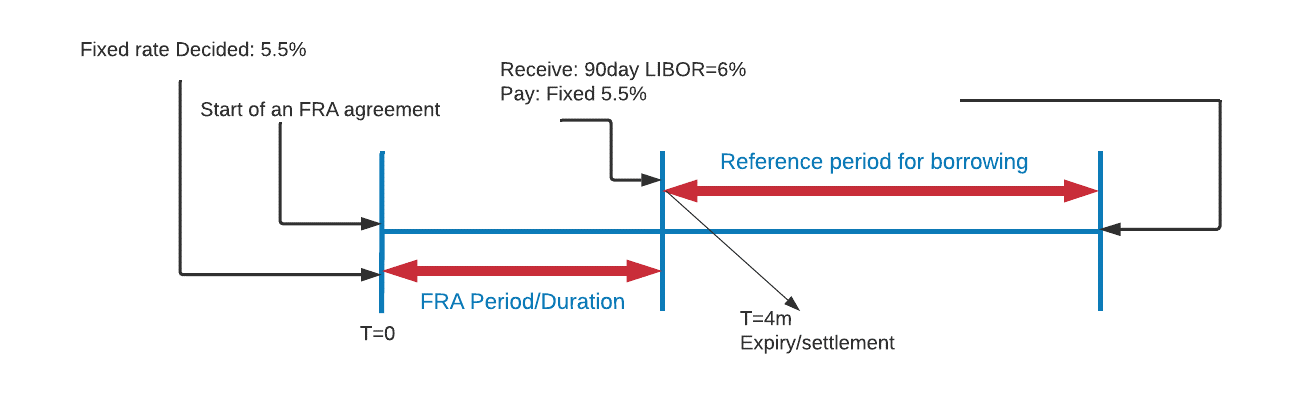
Since the settlement rate is higher (6%) than the contract rate (5.5%), the buyer will be receiving money from the seller. The payment to the long at settlement are as follow:

Interest saving:

$$=(6\%-5.5\%)\times\frac{90}{360}\times1\text{m}=1,250$$

Discounted back 90 days @ 6%:

$$=\frac{1,250}{[1+\frac{90}{360}\times6\%]}={1,231.53}$$

$$ \begin{array}{l|c|c} \textbf{Feature} & \textbf{Forward Rate Agreement (FRA)} & \textbf{Forward Contract} \\ \hline \text{Purpose} & \text{Interest Rate Hedging} & \text{Price Hedging} \\ \hline \text{Settlement} & \text{Cash-Settled} & \text{Physical Delivery} \\ \hline \text{Common Use} & \text{Loans & Borrowing Costs} & \text{Commodities, FX} \\ \hline \text{Tested In} & \text{CFA & FRM Exams} & \text{CFA & FRM Exams} \\ \end{array} $$  

View Full CFA Course  

Why Forward Rate Agreements Matter in CFA Level I

Forward rate agreements are important CFA Level I Derivatives concepts. Candidates may be tested on FRA notation, contract payoffs, settlement values, and how firms hedge future borrowing or lending rates using interest rate derivatives.

To strengthen your preparation, explore the CFA Level I study program with practice questions, mock exams, and guided lessons.